TL;DR#
3D reconstruction from multiple images is crucial, and 3D Gaussian Splatting (3DGS) offers real-time rendering with high-quality results. However, it suffers from issues like needle-like artifacts and suboptimal geometry due to Gaussians converging into anisotropic forms. This paper tackles these problems.
The authors propose using effective rank analysis to identify these needle-like shapes (effective rank 1). To address this, they introduce effective rank as a regularization term that constrains the structure of the Gaussians. This regularization enhances normal and geometry reconstruction while reducing artifacts. The method is easily integrated into existing 3DGS variants, improving their overall quality. The effective rank method is shown to be more effective than previous solutions, leading to higher-quality 3D models and improved accuracy.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses limitations in 3D Gaussian Splatting, a promising technique for real-time 3D reconstruction. By introducing effective rank analysis and regularization, it improves the accuracy and quality of 3D models, particularly by mitigating needle-like artifacts. This work is relevant to researchers in computer vision and graphics, offering a practical solution to enhance existing methods. It also opens up new avenues for research into shape statistics and regularization in implicit surface representation.
Visual Insights#

🔼 This figure compares the 3D mesh reconstruction results of different methods using Truncated Signed Distance Function (TSDF). It highlights the improvement achieved by incorporating the effective rank regularization. Baseline methods (without the regularization) tend to produce meshes with holes or incomplete surfaces. The proposed method, by promoting disk-like Gaussian primitives, generates more complete and artifact-free mesh reconstructions.
read the caption
Figure 4: Visualization of the reconstructed mesh using TSDF. Baseline methods often exhibit empty holes, while our regularization term enforces disk-like Gaussians, reducing such artifacts and improving surface reconstruction.

🔼 This table presents a quantitative comparison of Chamfer distance and PSNR (Peak Signal-to-Noise Ratio) metrics across different methods for 3D reconstruction on the DTU dataset. It shows the performance of several baseline methods (3DGS, SuGaR, 2DGS, GOF) both with and without the proposed effective rank regularization. Each row represents a different method, and the columns represent Chamfer distances and PSNR values for different scenes (24, 37, 40, etc.) within the DTU dataset. The ‘Mean’ and ‘Std’ columns provide the average and standard deviation of the Chamfer distances across all scenes. The ‘PSNR’ column shows the peak signal-to-noise ratio values.
read the caption
Table 1: Chamfer distance and PSNR report on DTU dataset. +e denotes the erank regularization.
In-depth insights#
3DGS Enhancements#
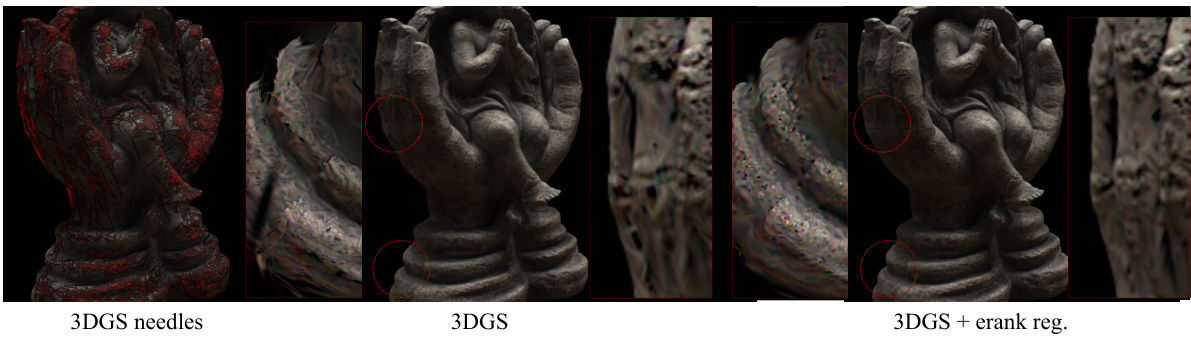
3D Gaussian Splatting (3DGS) enhancements predominantly focus on addressing limitations of the original method. Needle-like artifacts, a significant visual flaw, are a primary target, tackled via techniques like effective rank regularization. This approach analyzes the shape statistics of Gaussian primitives, constraining their structure to prevent the convergence into undesirable needle shapes. Improvements in normal and geometry reconstruction are also key goals, achieved by methods such as the effective rank regularization that promote the generation of more disk-like and less needle-like Gaussian primitives. These improvements directly enhance visual fidelity and rendering quality, making 3DGS more suitable for real-time applications where speed and visual accuracy are crucial. In summary, 3DGS enhancements aim for a balanced improvement between rendering quality, geometric accuracy and computational efficiency, thereby expanding the range of applications that 3DGS can effectively serve.
Effective Rank#
The concept of “Effective Rank” offers a novel approach to analyzing the shape statistics of 3D Gaussian primitives within the context of 3D reconstruction. It addresses limitations of prior methods that focus solely on individual variances, providing a more comprehensive understanding of Gaussian geometry. By using effective rank as a regularization term, the authors directly constrain the structure of the Gaussians, improving normal and geometry reconstruction while significantly reducing needle-like artifacts. This differentiable metric allows for integration into existing optimization frameworks, making the proposed technique easily adaptable and broadly applicable to enhance various 3D Gaussian splatting variants. The effectiveness is demonstrated by a marked improvement in visual fidelity and a reduction in computational demands, showcasing a powerful strategy for enhancing the quality and efficiency of 3D reconstruction algorithms.
Regularization#
The concept of regularization is crucial in addressing the challenges of 3D Gaussian splatting, particularly the issues of needle-like artifacts and suboptimal geometries. The authors cleverly employ effective rank analysis to characterize the shape statistics of 3D Gaussian primitives, revealing a tendency towards needle-like structures. This insight motivates the introduction of effective rank as a novel regularization term. The regularization effectively constrains the structure of the Gaussians, preventing them from collapsing into undesirable shapes. This, in turn, leads to improved normal and geometry reconstruction and significantly reduces the occurrence of needle-like artifacts, ultimately enhancing the quality of 3D reconstruction without sacrificing visual fidelity. The method’s effectiveness is demonstrated by its seamless integration as an add-on module to existing 3DGS variants, further highlighting its practicality and versatility. The differentiable nature of effective rank ensures compatibility with standard optimization frameworks, thereby enhancing the overall optimization process. Furthermore, a comparison with existing regularization techniques such as SuGaR and 2DGS shows the superiority of the proposed method in controlling the shapes of the Gaussian primitives.
Needle Artifact Reduction#
Needle-like artifacts, a common issue in 3D Gaussian splatting (3DGS) methods, severely impact the quality of reconstructed surfaces. These artifacts manifest as spiky, unrealistic protrusions that detract from visual fidelity. Effective rank analysis offers a novel approach to addressing this issue. By analyzing the shape statistics of Gaussian primitives, particularly focusing on their effective rank, the method identifies those Gaussians that have converged into problematic needle-like shapes. The core of the solution involves using effective rank as a regularization term to constrain the shape of the Gaussians during training, encouraging the formation of more desirable, disk-like primitives. This prevents the convergence of Gaussian distributions into highly anisotropic forms, thereby mitigating the needle artifacts and significantly improving the overall quality of 3D reconstruction and novel view synthesis. The approach acts as a plug-and-play module, adaptable to different 3DGS variations and improving geometry and normal estimation. The method’s efficacy is demonstrated through both qualitative and quantitative results, showcasing its practical relevance in the domain.
Future Work#
Future research directions could explore extending the effective rank regularization to encompass higher-order interactions between Gaussians, moving beyond individual primitive analysis. This might involve incorporating graph neural networks or other techniques to model spatial dependencies. Further investigation into the optimal choice of the regularization hyperparameter is also needed, perhaps through adaptive methods or techniques that learn the parameter during training. Additionally, researchers could investigate the impact of different primitive representations, beyond 3D Gaussians, on both accuracy and efficiency. The use of other implicit surface representations might offer improvements in specific application domains. Finally, exploring integration with other 3D reconstruction methods could enhance the overall system’s robustness and versatility, especially in handling scenarios with challenging conditions or noisy data. Careful consideration of the trade-offs between accuracy, speed and memory efficiency is crucial in guiding future developments.
More visual insights#
More on figures
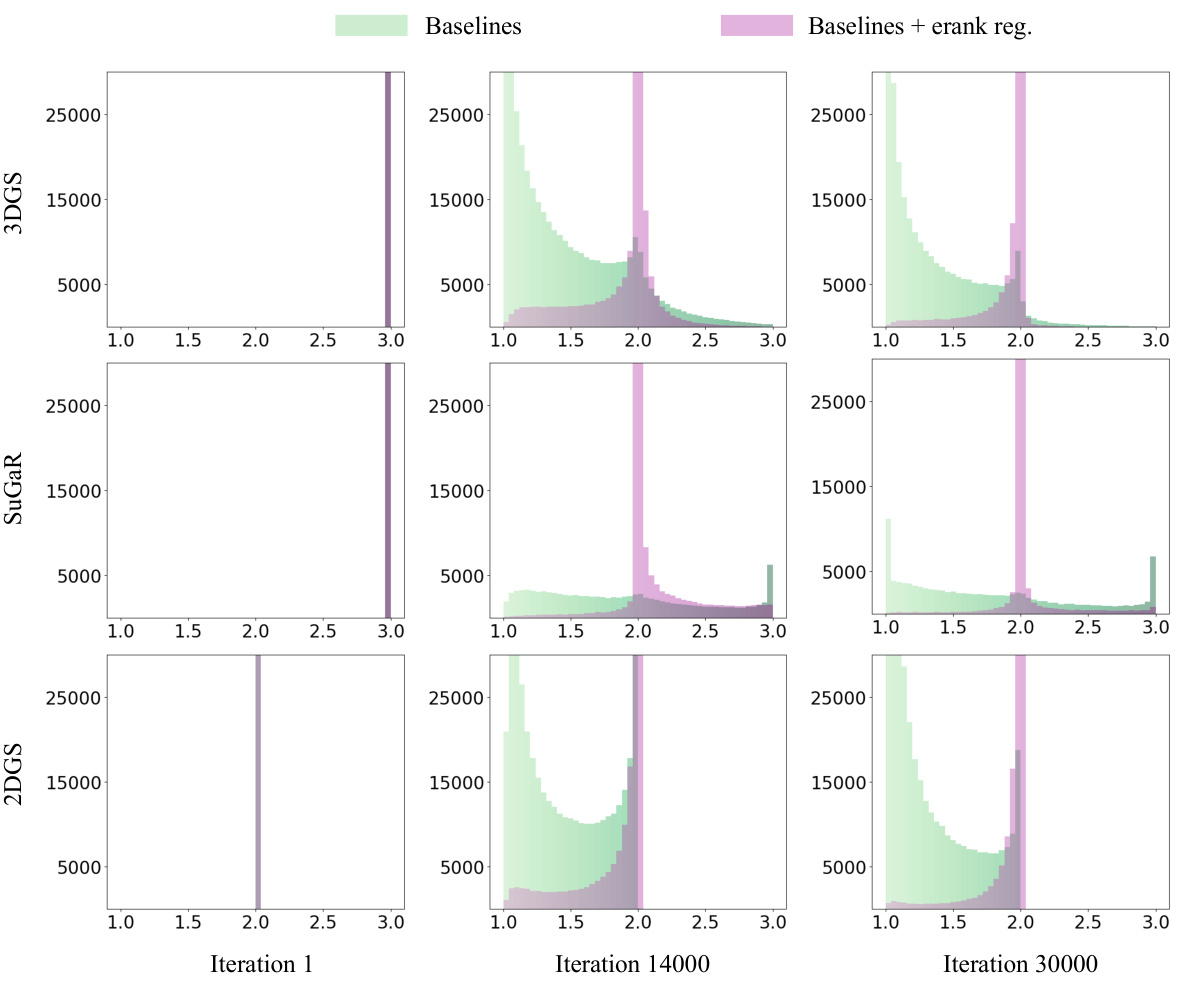
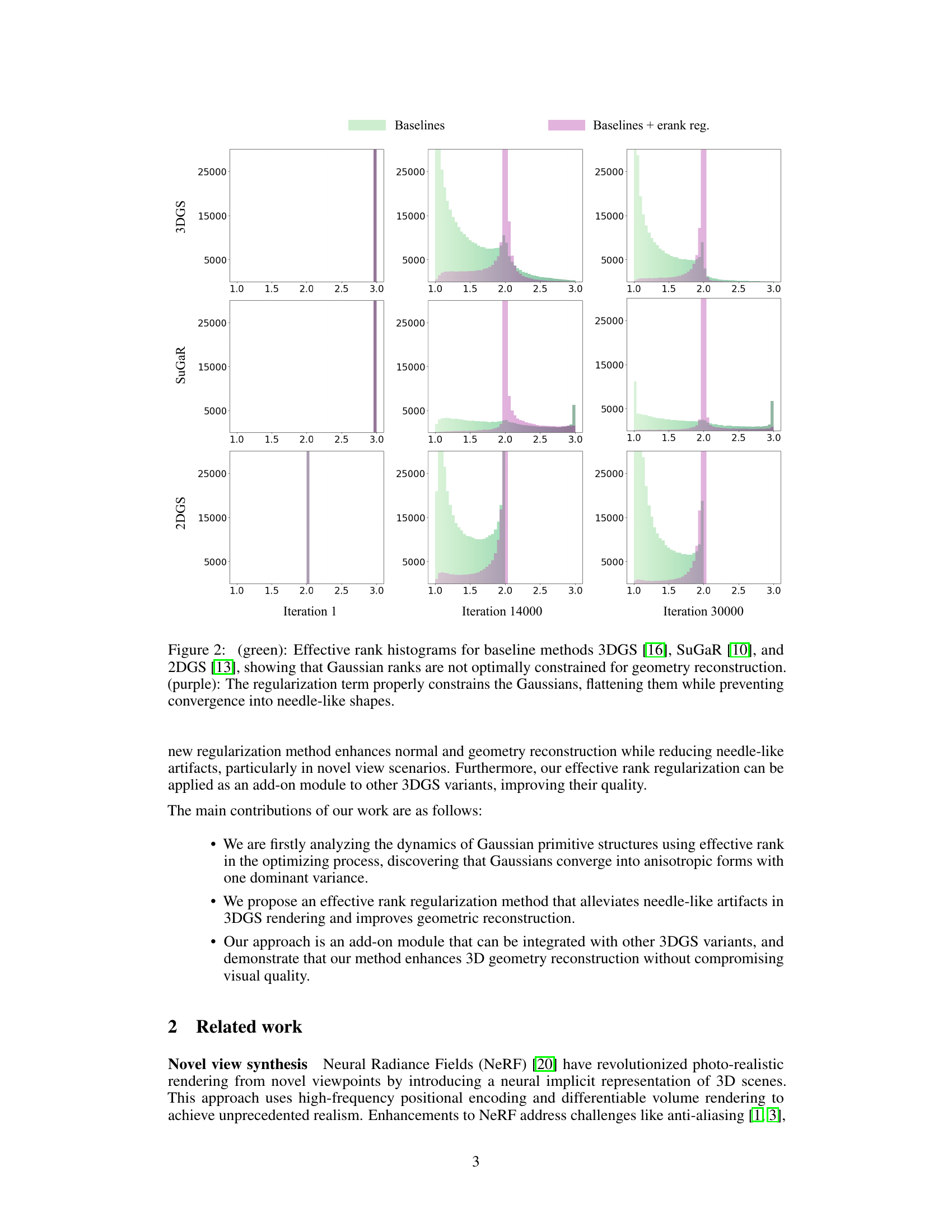
🔼 This figure shows the distribution of effective ranks of 3D Gaussians in three different methods (3DGS, SuGaR, 2DGS) at different training iterations. The green histograms represent the baseline methods, while the purple histograms show the results after applying the proposed effective rank regularization. The histograms illustrate how the regularization helps prevent Gaussians from collapsing into needle-like shapes (effective rank close to 1), leading to better geometry reconstruction.
read the caption
Figure 2: (green): Effective rank histograms for baseline methods 3DGS [16], SuGaR [10], and 2DGS [13], showing that Gaussian ranks are not optimally constrained for geometry reconstruction. (purple): The regularization term properly constrains the Gaussians, flattening them while preventing convergence into needle-like shapes.
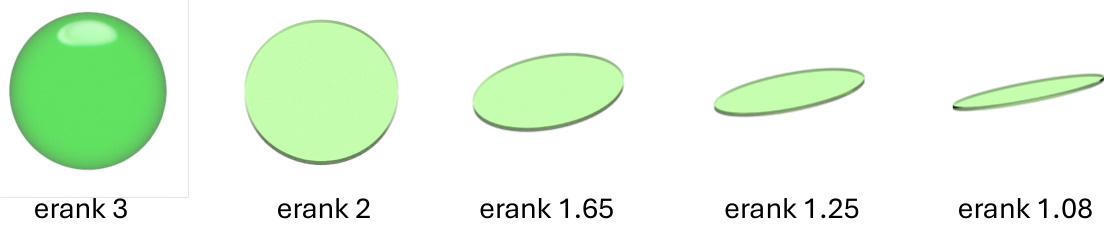
🔼 This figure visualizes 3D spheres and 2D disks with varying effective ranks. The effective rank, a measure of the shape’s dimensionality, is shown to decrease as the shape becomes more elongated. The image demonstrates the relationship between effective rank and the visual appearance of the Gaussian primitive, which is crucial for understanding the proposed effective rank regularization method in the paper.
read the caption
Figure 3: Real-scale visualization of a 3D sphere and 2D disks and their effective ranks.

🔼 This figure compares the 3D mesh reconstruction results of four different methods: SuGaR, 2DGS, GOF, and GOF with effective rank regularization. The image shows a scene with scissors resting on some concrete blocks. The figure highlights that baseline methods (SuGaR, 2DGS, GOF) result in meshes with noticeable holes or missing geometry, while the method with effective rank regularization produces a more complete and accurate mesh reconstruction, demonstrating its effectiveness in mitigating artifacts and improving surface quality.
read the caption
Figure 4: Visualization of the reconstructed mesh using TSDF. Baseline methods often exhibit empty holes, while our regularization term enforces disk-like Gaussians, reducing such artifacts and improving surface reconstruction.
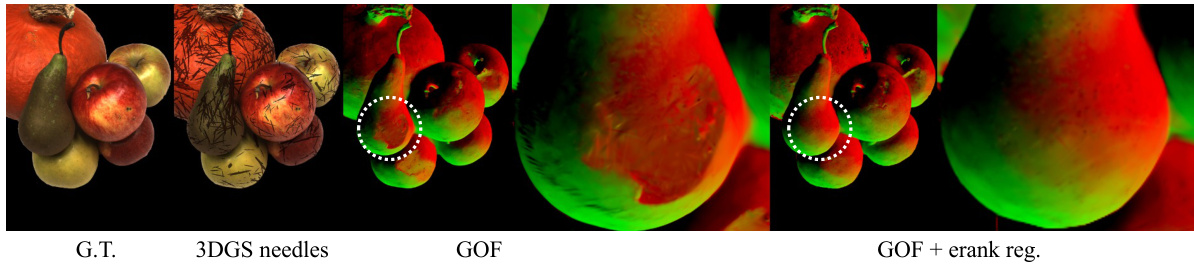
🔼 This figure shows a comparison of mesh reconstruction results using TSDF (Truncated Signed Distance Function) for four different methods: Ground Truth (G.T.), 3DGS (3D Gaussian Splatting) with needle-like artifacts, GOF (Gaussian Opacity Fields), and GOF enhanced with the proposed effective rank regularization. The image highlights how the baseline methods (3DGS and GOF) produce meshes with noticeable holes and incomplete surfaces, whereas the proposed method effectively fills in these gaps and leads to a more complete and accurate reconstruction.
read the caption
Figure 4: Visualization of the reconstructed mesh using TSDF. Baseline methods often exhibit empty holes, while our regularization term enforces disk-like Gaussians, reducing such artifacts and improving surface reconstruction.
🔼 This figure shows a qualitative comparison of novel view synthesis results on the DTU dataset between the baseline 3DGS method and the proposed method incorporating effective rank regularization. The leftmost image highlights Gaussians with an effective rank less than 1.02 in red, illustrating the needle-like artifacts that the baseline method produces. The images in the middle show the novel view synthesis results produced by the baseline 3DGS method, while the rightmost images display the results obtained using the method with effective rank regularization. The comparison demonstrates the effectiveness of the proposed method in mitigating needle-like artifacts and improving the visual quality of novel views.
read the caption
Figure 6: Qualitative comparison on DTU dataset. Gaussians with erank(Gk) < 1.02 are visualized in red. Our regularization term mitigates needle-like artifacts in novel views.

🔼 The figure shows a qualitative comparison of novel view synthesis results on the Mip-NeRF360 dataset. The left shows the results from the baseline 3DGS method, while the right shows the results from the 3DGS method enhanced with the proposed effective rank regularization. The enhanced method demonstrates improved visual quality and a more compact representation, particularly in rendering thin objects such as the bicycle’s spokes, which appear less noisy and more defined.
read the caption
Figure 7: Qualitative comparison on Mip-NeRF360 dataset. Our method effectively represents thin objects, achieving better visual quality and compactness
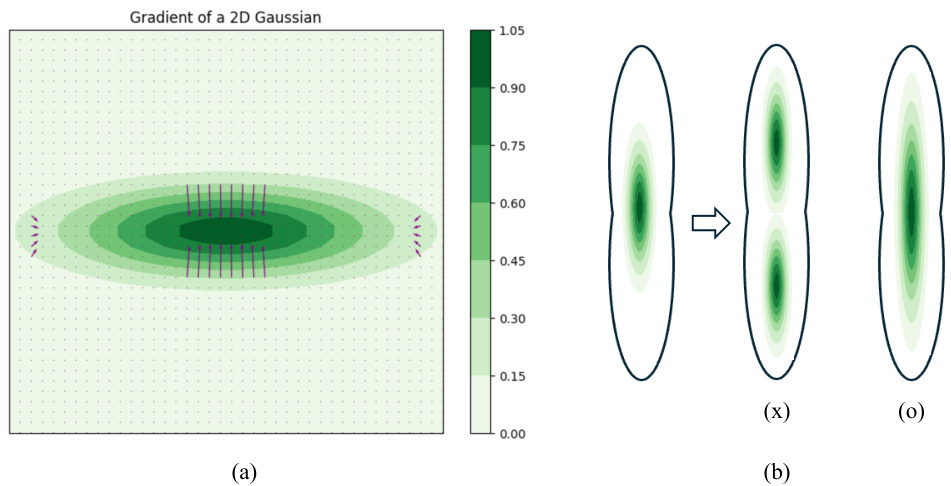
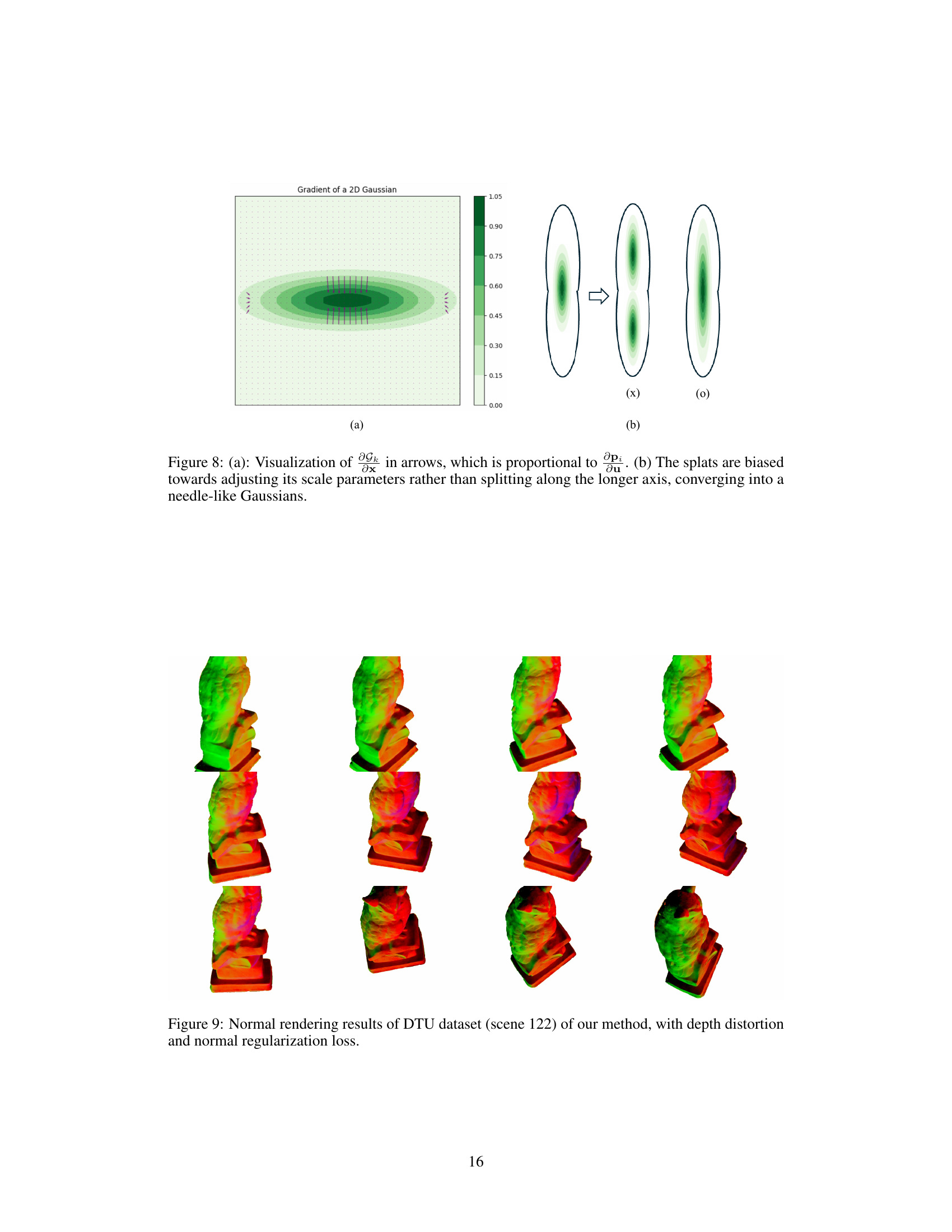
🔼 This figure shows the visualization of the gradient of a 2D Gaussian and the effect of the gradient on the splitting of Gaussians. In (a), the gradient is visualized with arrows, showing that the gradient is proportional to the pixel gradient. In (b), it is shown that the splats are biased towards adjusting their scale parameters rather than splitting along the longer axis, resulting in needle-like Gaussians. This phenomenon is due to the fact that the gradient along the longer axis is typically small, so the splats are not effectively densified along the longer axis.
read the caption
Figure 8: (a): Visualization of ∂Gk/∂x in arrows, which is proportional to ∇pᵢ. (b) The splats are biased towards adjusting its scale parameters rather than splitting along the longer axis, converging into a needle-like Gaussians.

🔼 This figure shows a qualitative comparison of novel view synthesis results on the DTU dataset between the baseline 3DGS method and the proposed method with effective rank regularization. The left side displays images generated by the baseline 3DGS, revealing noticeable needle-like artifacts, particularly in novel views. These artifacts are represented by the red-colored Gaussians, indicating that their effective rank is less than 1.02, signifying a highly anisotropic, needle-like shape. The right side shows the corresponding results obtained using the proposed method, which effectively mitigates these artifacts by constraining the structure of the Gaussians and improving their quality in novel views.
read the caption
Figure 6: Qualitative comparison on DTU dataset. Gaussians with erank(Gk) < 1.02 are visualized in red. Our regularization term mitigates needle-like artifacts in novel views.

🔼 This figure shows a comparison of normal and visual rendering results for scene 55 from the DTU dataset. The left half displays the grayscale normal rendering, while the right half shows the visual rendering with color information. The goal is to illustrate the improvement in reconstruction quality achieved by the proposed method (with depth distortion and normal regularization loss). The comparison highlights a reduction in artifacts (like missing parts or hollow regions) that frequently occur in naive 3D Gaussian Splatting.
read the caption
Figure 10: Normal rendering and visual rendering results of DTU dataset (scene 55) of our method, with depth distortion and normal regularization loss.

🔼 The figure shows a qualitative comparison of novel view synthesis results on the Mip-NeRF360 dataset. The left side displays renderings from the baseline 3DGS method, showing artifacts and less detail, particularly in thin objects like the bicycle. The right side shows results from the proposed method, which uses effective rank regularization. The improvements are clear in terms of increased visual quality and a more compact representation of the scene, particularly in the bicycle’s details.
read the caption
Figure 7: Qualitative comparison on Mip-NeRF360 dataset. Our method effectively represents thin objects, achieving better visual quality and compactness.
More on tables

🔼 This table presents a quantitative evaluation of the proposed method and baseline methods on the DTU dataset for geometry reconstruction. It shows Chamfer distance and PSNR values for different scenes in the dataset. The ‘+e’ indicates the inclusion of the effective rank regularization. Lower Chamfer distance and higher PSNR values indicate better reconstruction quality.
read the caption
Table 1: Chamfer distance and PSNR report on DTU dataset. +e denotes the erank regularization.
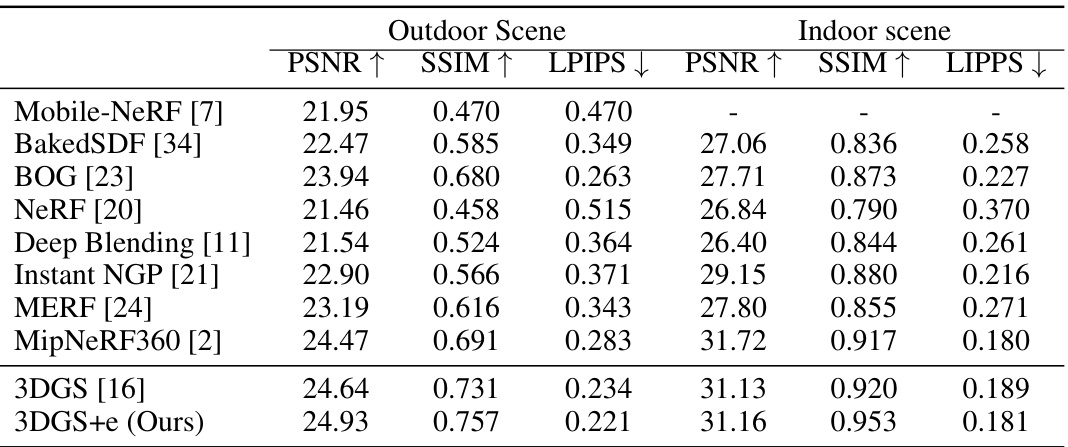
🔼 This table presents a quantitative comparison of different novel view synthesis methods on the Mip-NeRF 360 dataset. The metrics used are PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index), and LPIPS (Learned Perceptual Image Patch Similarity). Higher PSNR and SSIM values indicate better image quality, while lower LPIPS values suggest better perceptual similarity to ground truth images. The table allows for a direct comparison of the proposed method’s performance against several state-of-the-art techniques, highlighting its improvements in novel view synthesis quality.
read the caption
Table 3: Quantitative results on Mip-NeRF 360 [2] dataset.
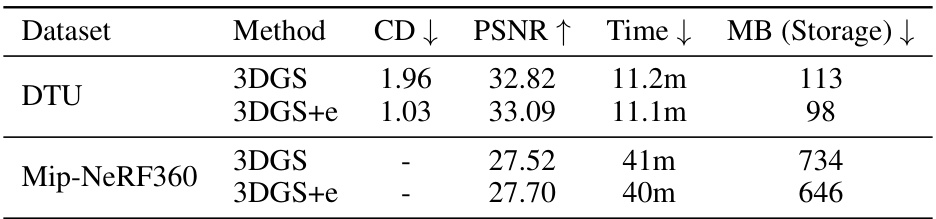
🔼 This table presents a quantitative comparison of the proposed method (3DGS+e) against the baseline method (3DGS) in terms of storage usage (MB), Chamfer distance (CD), PSNR, and training time. The comparison is shown for two datasets: DTU and Mip-NeRF360. Lower CD values indicate better geometry reconstruction accuracy, higher PSNR values represent better image quality, and lower training times are preferred. The table highlights the improvements achieved by the proposed method in terms of both accuracy and efficiency.
read the caption
Table 4: Storage usage of our method, along with Chamfer distance, PSNR, and optimization time.
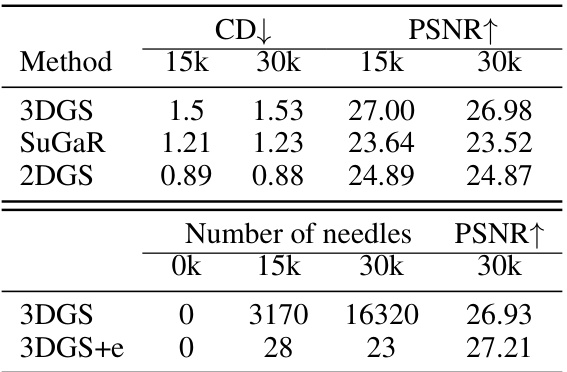
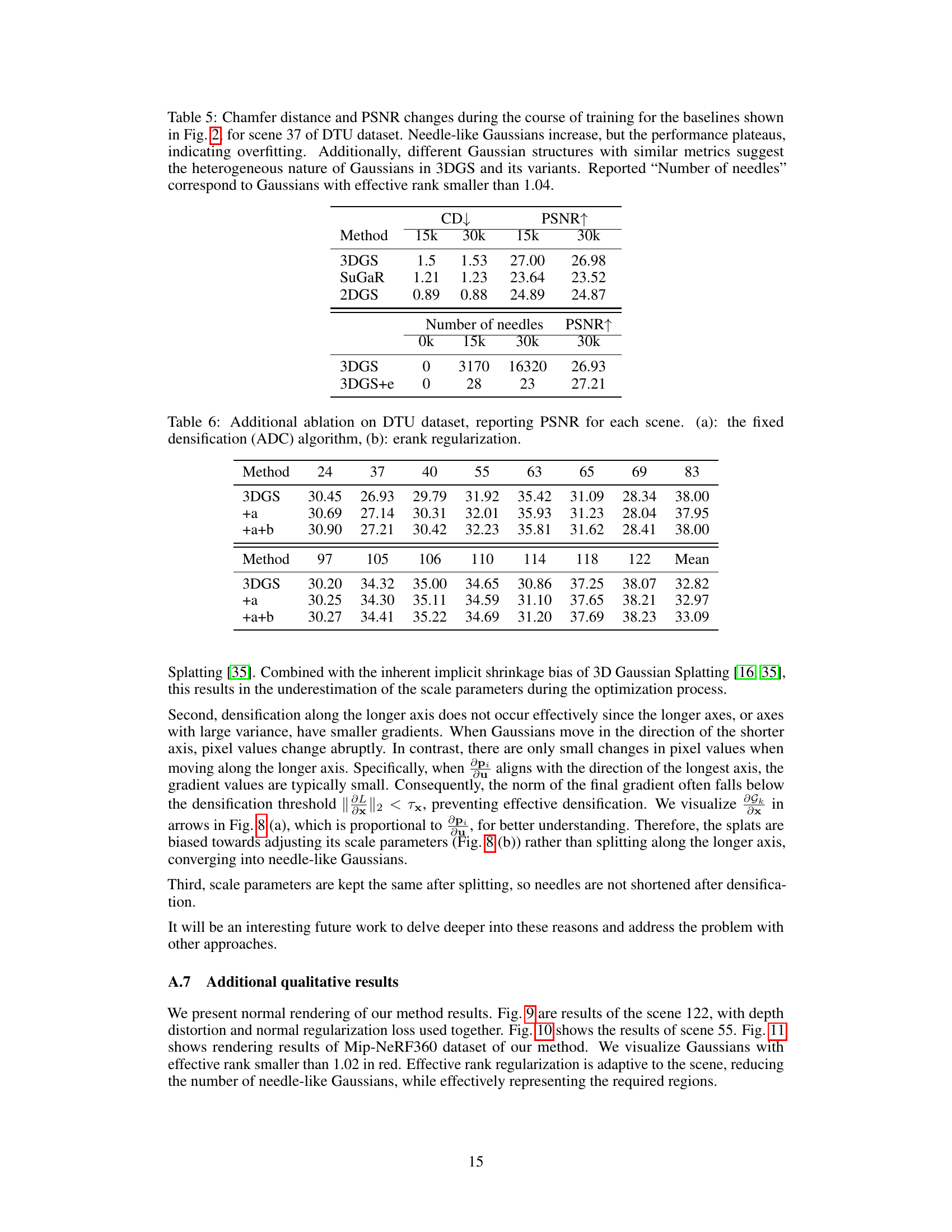
🔼 This table presents an ablation study on the effect of the proposed effective rank regularization on the baseline methods (3DGS, SuGaR, and 2DGS) for scene 37 of the DTU dataset. It shows the Chamfer distance and PSNR at 15k and 30k iterations, highlighting how needle-like Gaussians increase while performance plateaus, indicating overfitting. The table also demonstrates that even with comparable performance metrics, the underlying Gaussian structures in baseline methods are heterogeneous.
read the caption
Table 5: Chamfer distance and PSNR changes during the course of training for the baselines shown in Fig. 2, for scene 37 of DTU dataset. Needle-like Gaussians increase, but the performance plateaus, indicating overfitting. Additionally, different Gaussian structures with similar metrics suggest the heterogeneous nature of Gaussians in 3DGS and its variants. Reported 'Number of needles' correspond to Gaussians with effective rank smaller than 1.04.
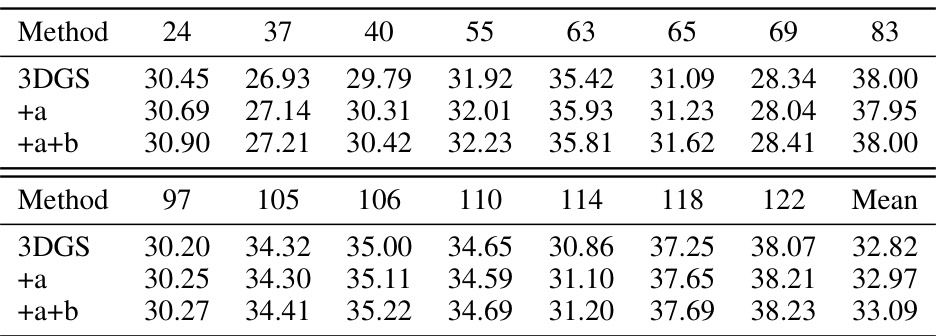
🔼 This table presents a quantitative comparison of Chamfer distance and PSNR (Peak Signal-to-Noise Ratio) on the DTU (Danish Technical University) dataset for different methods. It compares the baseline 3DGS method to variations incorporating the proposed effective rank regularization (+e). SuGaR, 2DGS, and GOF methods are also included for comparison. Lower Chamfer distance values indicate better geometry reconstruction, while higher PSNR values represent better image quality.
read the caption
Table 1: Chamfer distance and PSNR report on DTU dataset. +e denotes the erank regularization.
Full paper#