TL;DR#
Many existing out-of-distribution (OOD) detection methods struggle in real-world applications due to imbalanced data distributions. This often leads to misidentification of in-distribution (ID) samples as OOD (tail classes) or vice-versa (OOD samples as head classes), hindering the accuracy of OOD detection. This paper identifies this critical issue and proposes a new solution.
The paper introduces ImOOD, a generalized statistical framework that analyzes the OOD problem under imbalanced data. ImOOD reveals a class-aware bias, and then proposes a unified training-time regularization technique to address this bias and improve performance. Extensive experiments on standard benchmarks (CIFAR10-LT, CIFAR100-LT, ImageNet-LT) demonstrate consistent improvements against state-of-the-art OOD detection methods. This contribution is significant as it provides a theoretically-grounded method for addressing the challenge of imbalanced data in OOD detection.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on out-of-distribution (OOD) detection, especially in real-world scenarios with imbalanced data. It offers a novel theoretical framework and a unified regularization method to significantly improve the performance of OOD detectors, addressing a critical limitation of existing methods. This work also opens avenues for future research in developing more robust and reliable OOD detection techniques.
Visual Insights#

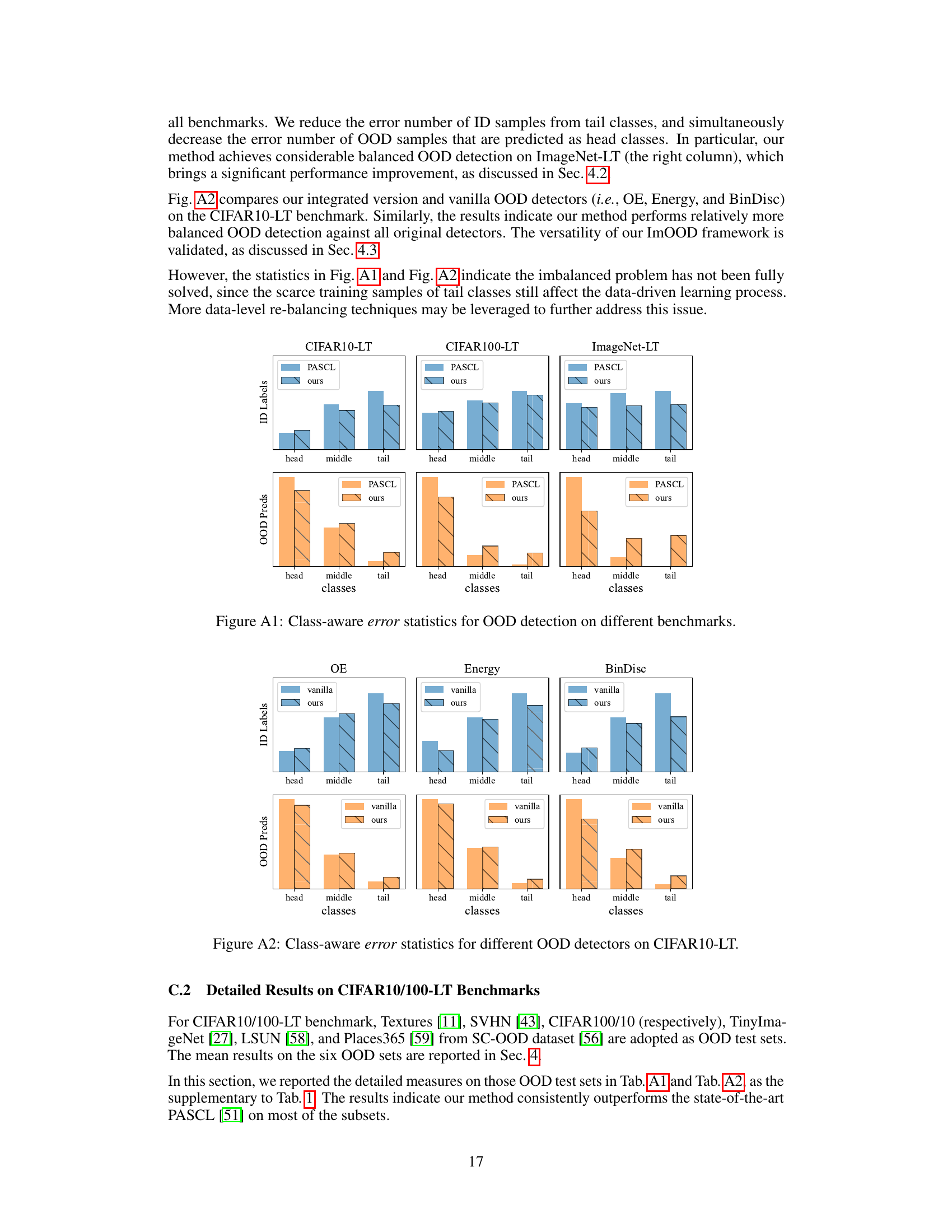
🔼 This figure illustrates two common issues in out-of-distribution (OOD) detection with imbalanced data. Subfigure (a) shows statistical analyses of misclassified samples. It reveals that tail classes (less frequent classes) within the in-distribution (ID) data are often misidentified as OOD samples, while head classes (more frequent) within the ID data incorrectly classify OOD samples as belonging to the ID. Subfigure (b) provides a visual representation in feature space illustrating how the disproportionate decision space sizes of head and tail classes contribute to these errors.
read the caption
Figure 1: Issues of OOD detection on imbalanced data. (a) Statistics of the class labels of ID samples that are wrongly detected as OOD, and the class predictions of OOD samples that are wrongly detected as ID. (b) Illustration of the OOD detection process in feature space. Head classes' huge decision space and tail classes' small decision space jointly damage the OOD detection.

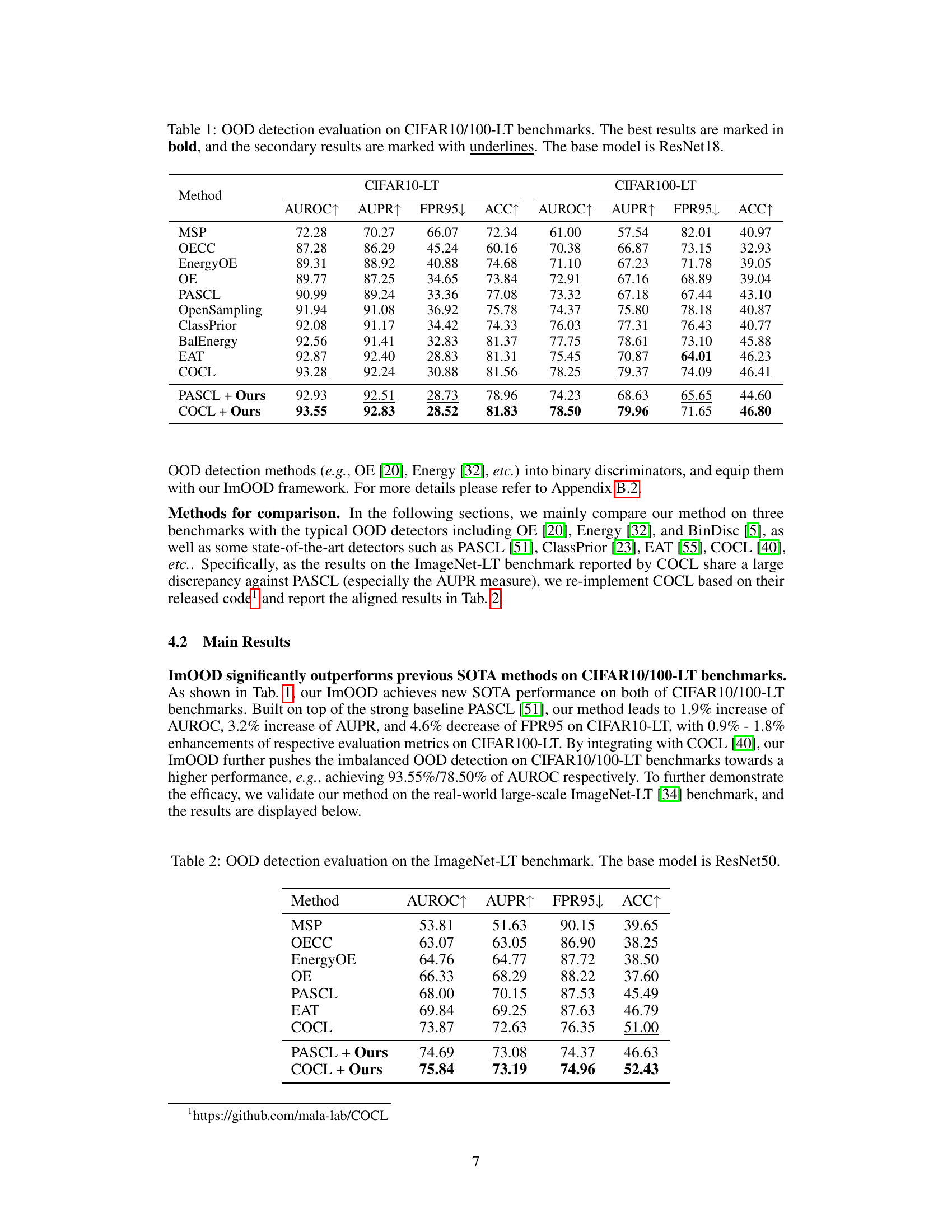
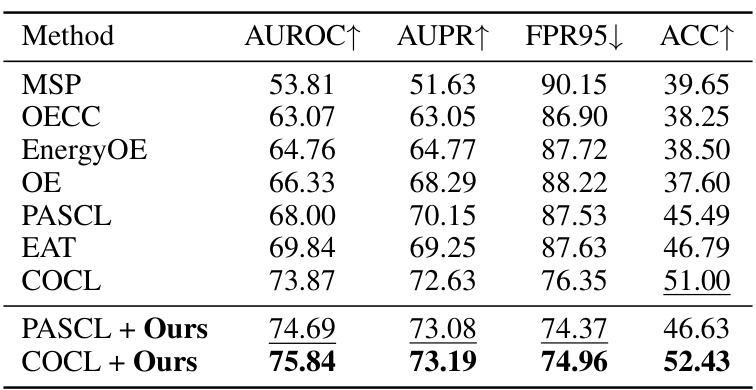
🔼 This table presents the results of out-of-distribution (OOD) detection experiments conducted on the CIFAR10-LT and CIFAR100-LT benchmark datasets. The table compares various OOD detection methods, including baseline methods and methods enhanced by the proposed ImOOD approach. The performance metrics shown are AUROC (Area Under the Receiver Operating Characteristic curve), AUPR (Area Under the Precision-Recall curve), FPR95 (False Positive Rate at 95% True Positive Rate), and the in-distribution classification accuracy (ACC). The best performance for each metric is shown in bold, and the second-best is underlined. ResNet18 is used as the base model for all methods.
read the caption
Table 1: OOD detection evaluation on CIFAR10/100-LT benchmarks. The best results are marked in bold, and the secondary results are marked with underlines. The base model is ResNet18.
In-depth insights#
Imbalanced OOD#
The concept of “Imbalanced OOD” (Out-of-Distribution) detection highlights a critical weakness in many existing OOD detection methods. Traditional approaches often assume a balanced distribution of in-distribution (ID) and OOD data, which rarely holds in real-world scenarios. Imbalanced datasets, particularly those with long-tailed distributions, introduce significant challenges. The core problem lies in the disproportionate representation of classes within the ID data. This leads to poor performance in detecting OOD samples that are similar to under-represented ID classes (tail classes) and misclassifying OOD samples as high-frequency ID samples (head classes). Addressing this imbalance requires methods that go beyond simple thresholding of anomaly scores, instead necessitating a more nuanced understanding of class distributions and employing strategies to alleviate the bias introduced by class imbalance. Solutions might involve novel loss functions, data augmentation, or re-sampling techniques, specifically targeting tail classes, to improve the overall separability between ID and OOD data. The ultimate goal is to create robust OOD detectors that generalize well to real-world scenarios with their inherently skewed distributions.
ImOOD Framework#
The ImOOD framework presents a novel statistical approach to address the limitations of existing OOD detection methods, particularly in the context of imbalanced data distributions. It theoretically analyzes the class-aware bias that arises from the disparity between decision spaces of head and tail classes in long-tailed datasets. This leads to a unified training-time regularization technique that mitigates this bias by promoting separability between tail classes and OOD samples and preventing the misclassification of OOD samples as head classes. The framework’s strength lies in its generalizability across various OOD detection methods and architectures. It provides a consistent, theoretically-grounded methodology backed by empirical evidence of improved performance on various benchmarks.
Bias Mitigation#
The concept of bias mitigation is crucial in machine learning, particularly when dealing with imbalanced datasets. Addressing biases is essential for fairness and to avoid discriminatory outcomes. In the context of out-of-distribution (OOD) detection, bias mitigation strategies often focus on resolving discrepancies in the decision boundaries of classifiers trained on imbalanced data. The head classes, being over-represented, might dominate the decision space, leading to misclassification of tail class samples as OOD and vice versa. Therefore, effective bias mitigation techniques aim to recalibrate these decision boundaries. This could involve adjusting class weights, employing data augmentation strategies to oversample tail classes or undersample head classes, or using regularization techniques to reduce the influence of the head classes during model training. Careful consideration of the statistical properties of the imbalanced data is key to select the appropriate mitigation method. Evaluating the effectiveness of bias mitigation approaches requires careful evaluation metrics which go beyond simple accuracy and consider the impact on both ID and OOD detection rates across different classes. The success of bias mitigation strategies heavily relies on a comprehensive understanding of the underlying data distribution and the inherent biases introduced by that imbalance.
Empirical Results#
An ‘Empirical Results’ section in a research paper would typically present the quantitative findings that support or refute the study’s hypotheses. A strong section would not only report key metrics (e.g., accuracy, precision, recall) but also provide detailed breakdowns to reveal nuanced trends. For instance, analyzing performance across different subgroups within the data (e.g., demographic categories or types of input) can uncover unexpected interactions or biases. Visualizations, such as graphs and tables, are crucial for effectively communicating these complex results. Statistical significance testing should be rigorously applied to ensure that observed differences aren’t due to random chance. Furthermore, a thoughtful discussion is needed, comparing the results to prior work and acknowledging any limitations of the experimental setup. This allows readers to assess the robustness and generalizability of the findings. A comprehensive analysis, linking the empirical observations back to the theoretical framework, is also vital to demonstrate a thorough understanding of the research problem.
Future Works#
The paper’s findings on imbalanced out-of-distribution (OOD) detection open several avenues for future work. A key area is to explore more sophisticated techniques for estimating the class-aware bias term, moving beyond the current parametric approach. This could involve developing non-parametric methods or incorporating prior knowledge about class distributions. Furthermore, research into adaptive regularization strategies that dynamically adjust to the data’s characteristics during the training process would significantly improve robustness. Investigating the impact of different loss functions and optimization algorithms in conjunction with the proposed regularization technique would refine the method’s efficacy. Finally, extensive evaluation on a broader range of datasets and model architectures is crucial to validate the generalizability of this approach and uncover any limitations in diverse real-world scenarios. The extension to other OOD detection methods and its adaptation to different data modalities, such as time series or text data, is also a worthwhile consideration.
More visual insights#
More on figures

🔼 This figure shows two common problems in out-of-distribution (OOD) detection with imbalanced data. The first part (a) presents statistics on the misclassification of in-distribution (ID) samples as OOD (mostly from tail classes) and the misclassification of OOD samples as ID (mostly head classes). The second part (b) illustrates this in feature space, showing that the large decision boundary of head classes and the small decision boundary of tail classes create conditions where OOD samples are more likely to be misclassified as head classes and tail classes are misclassified as OOD.
read the caption
Figure 1: Issues of OOD detection on imbalanced data. (a) Statistics of the class labels of ID samples that are wrongly detected as OOD, and the class predictions of OOD samples that are wrongly detected as ID. (b) Illustration of the OOD detection process in feature space. Head classes' huge decision space and tail classes' small decision space jointly damage the OOD detection.

🔼 This figure illustrates two common problems in out-of-distribution (OOD) detection with imbalanced data. Subfigure (a) shows statistical results demonstrating that tail-class in-distribution (ID) samples are often misclassified as OOD, while head-class ID samples are incorrectly predicted for OOD samples. Subfigure (b) visually depicts how the disparity in decision space between head and tail classes in feature space negatively affects OOD detection performance. The large decision space for head classes increases the likelihood of OOD samples being misclassified as head classes, whereas the small decision space for tail classes leads to a higher probability of tail-class ID samples being misidentified as OOD.
read the caption
Figure 1: Issues of OOD detection on imbalanced data. (a) Statistics of the class labels of ID samples that are wrongly detected as OOD, and the class predictions of OOD samples that are wrongly detected as ID. (b) Illustration of the OOD detection process in feature space. Head classes' huge decision space and tail classes' small decision space jointly damage the OOD detection.

🔼 This figure illustrates two common challenges in out-of-distribution (OOD) detection with imbalanced data. Subfigure (a) presents bar charts showing the distribution of misclassified in-distribution (ID) samples (wrongly labeled as OOD) and misclassified OOD samples (wrongly labeled as ID). It highlights that tail classes in the ID data are more likely to be misclassified as OOD, while OOD samples are more often misclassified as head classes in the ID data. Subfigure (b) provides a visual representation in feature space, demonstrating how the large decision boundary of head classes and small decision boundary of tail classes exacerbate the problems of OOD detection. The unequal decision boundaries make it difficult for the model to distinguish between tail ID samples and OOD samples.
read the caption
Figure 1: Issues of OOD detection on imbalanced data. (a) Statistics of the class labels of ID samples that are wrongly detected as OOD, and the class predictions of OOD samples that are wrongly detected as ID. (b) Illustration of the OOD detection process in feature space. Head classes' huge decision space and tail classes' small decision space jointly damage the OOD detection.
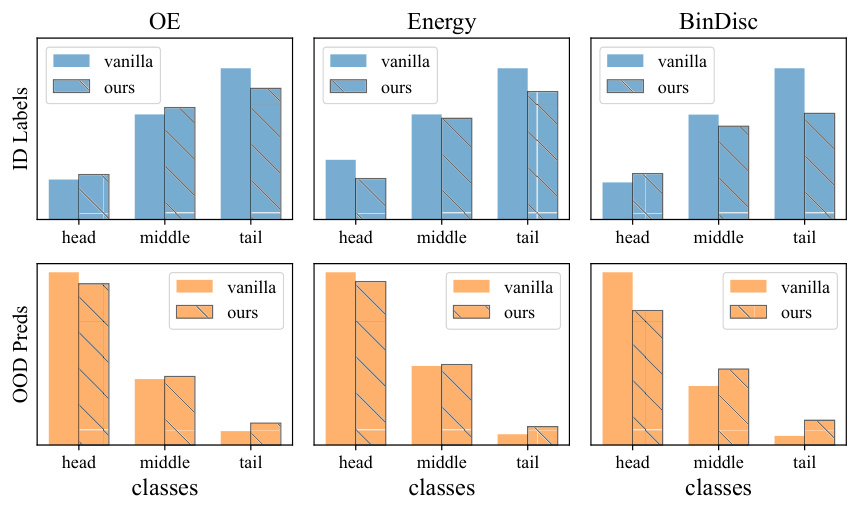
🔼 This figure shows the problems of out-of-distribution (OOD) detection on imbalanced data. Subfigure (a) presents statistics illustrating two common challenges: tail class samples from the in-distribution (ID) being misclassified as OOD, and OOD samples being misclassified as head class samples from the ID. Subfigure (b) provides a visualization in feature space, showcasing how the disproportionate decision spaces of head and tail classes negatively affect OOD detection performance.
read the caption
Figure 1: Issues of OOD detection on imbalanced data. (a) Statistics of the class labels of ID samples that are wrongly detected as OOD, and the class predictions of OOD samples that are wrongly detected as ID. (b) Illustration of the OOD detection process in feature space. Head classes' huge decision space and tail classes' small decision space jointly damage the OOD detection.
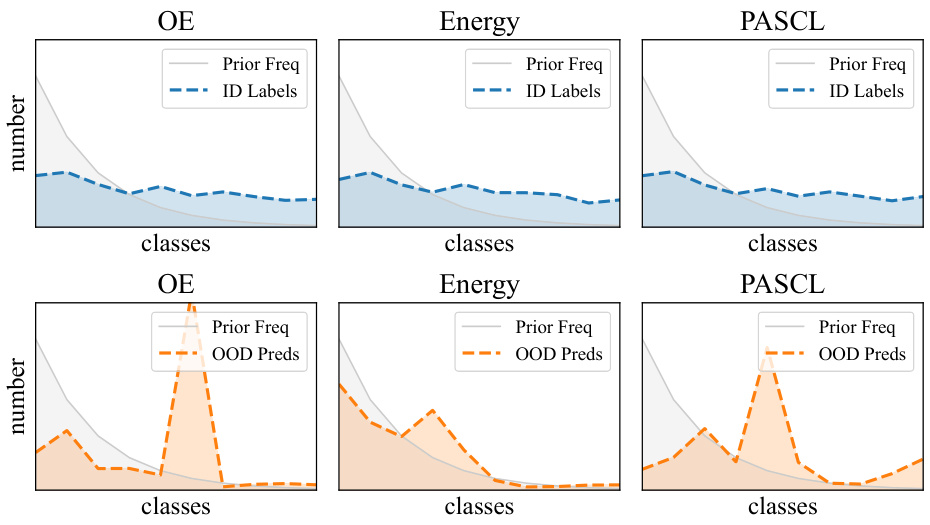
🔼 This figure shows the common issues in out-of-distribution (OOD) detection with imbalanced data. Subfigure (a) presents statistical analysis on wrongly classified in-distribution (ID) samples as OOD and wrongly classified OOD samples as ID. It demonstrates that tail classes in the ID data are frequently misclassified as OOD while OOD samples are often mistaken for head classes in the ID data. Subfigure (b) provides a visual illustration in feature space. The large decision boundary for head classes and the small decision space for tail classes are highlighted as the source of the performance degradation.
read the caption
Figure 1: Issues of OOD detection on imbalanced data. (a) Statistics of the class labels of ID samples that are wrongly detected as OOD, and the class predictions of OOD samples that are wrongly detected as ID. (b) Illustration of the OOD detection process in feature space. Head classes' huge decision space and tail classes' small decision space jointly damage the OOD detection.
More on tables
🔼 This table presents the results of out-of-distribution (OOD) detection experiments on the ImageNet-LT benchmark using ResNet50 as the base model. The table compares various OOD detection methods, including the proposed ImOOD method, showing their performance in terms of AUROC (Area Under the Receiver Operating Characteristic curve), AUPR (Area Under the Precision-Recall curve), FPR95 (False Positive Rate at 95% True Positive Rate), and ACC (accuracy). The results highlight the improved performance of the ImOOD method, particularly when combined with existing state-of-the-art methods like PASCL and COCL.
read the caption
Table 2: OOD detection evaluation on the ImageNet-LT benchmark. The base model is ResNet50.

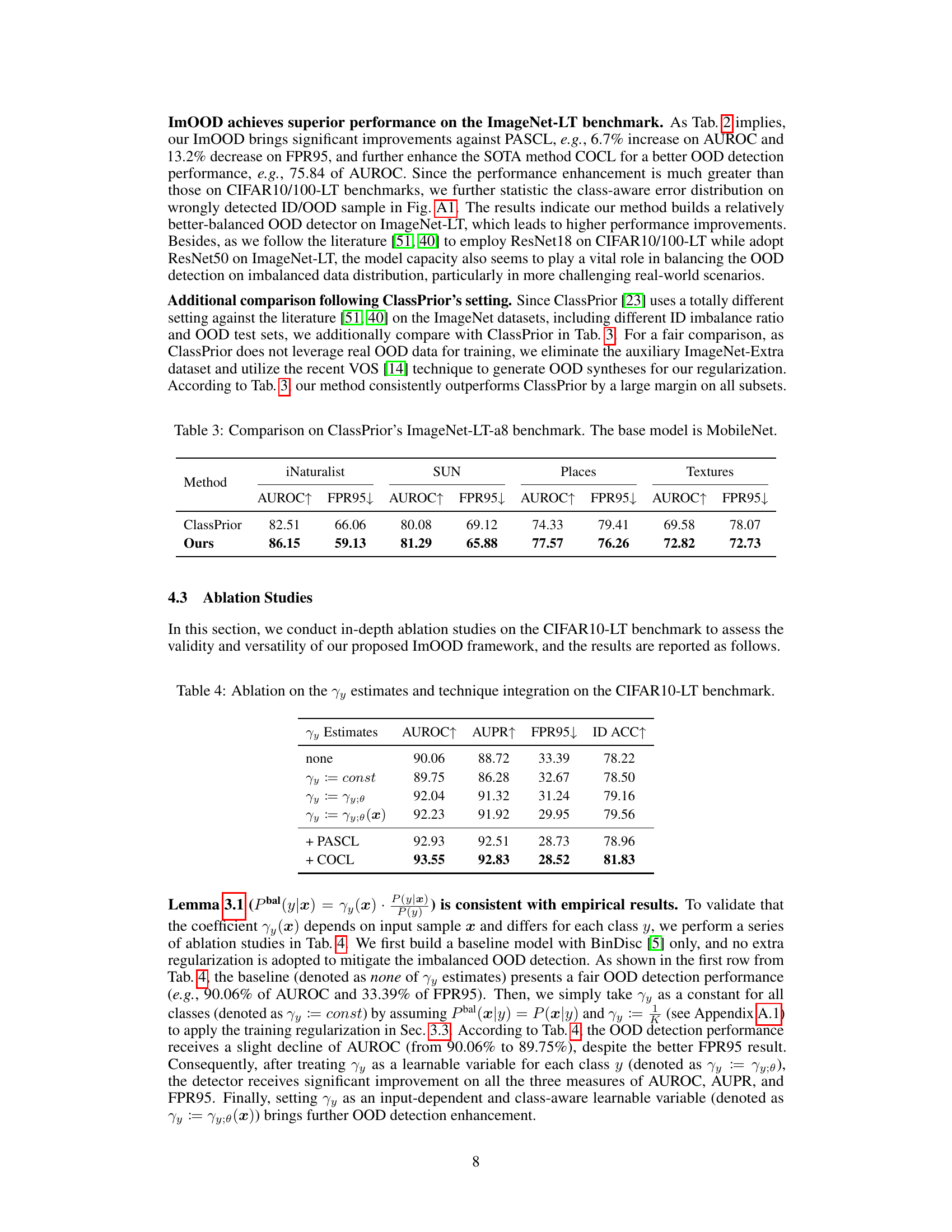
🔼 This table presents a comparison of the performance of the proposed ImOOD method against the ClassPrior method on the ImageNet-LT-a8 benchmark. The ImageNet-LT-a8 benchmark is a subset of the ImageNet-LT dataset with a specific long-tailed class distribution and uses MobileNet as the base model. The comparison uses AUROC and FPR95 metrics across four different subsets (iNaturalist, SUN, Places, and Textures) of the ImageNet-LT-a8 benchmark to evaluate the methods’ ability to detect out-of-distribution (OOD) samples. The results show that the ImOOD method significantly outperforms the ClassPrior method on all four subsets, demonstrating its superior performance in imbalanced OOD detection settings.
read the caption
Table 3: Comparison on ClassPrior's ImageNet-LT-a8 benchmark. The base model is MobileNet.
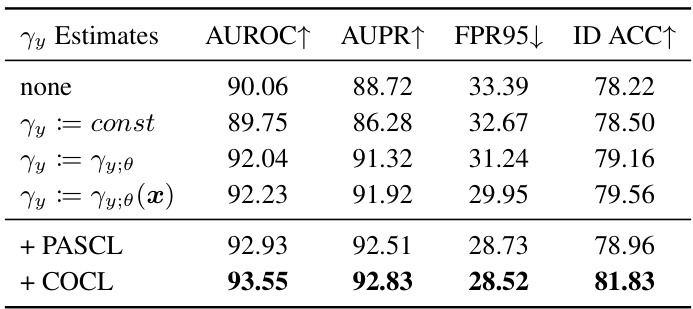
🔼 This table presents the results of ablation studies conducted on the CIFAR10-LT benchmark to evaluate the impact of different γy estimation methods and the integration of additional techniques (PASCL and COCL) on the overall performance of the proposed ImOOD framework. The table shows the AUROC, AUPR, FPR95, and ID ACC metrics for different configurations, allowing for a comparison of their effectiveness in mitigating the bias caused by imbalanced data distribution during OOD detection.
read the caption
Table 4: Ablation on the γy estimates and technique integration on the CIFAR10-LT benchmark.
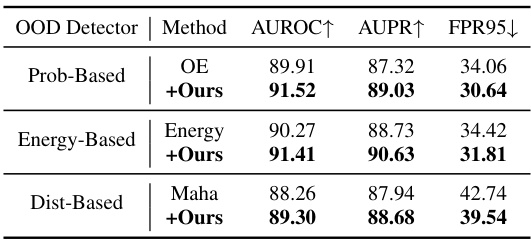
🔼 This table presents the results of applying the ImOOD framework to various OOD detection methods. It shows that ImOOD consistently improves the performance of different OOD detectors (Prob-Based, Energy-Based, and Dist-Based) across multiple evaluation metrics (AUROC, AUPR, and FPR95). The results demonstrate that ImOOD is a generalizable framework that can be applied to various OOD detectors.
read the caption
Table 5: Generalization to OOD detectors.
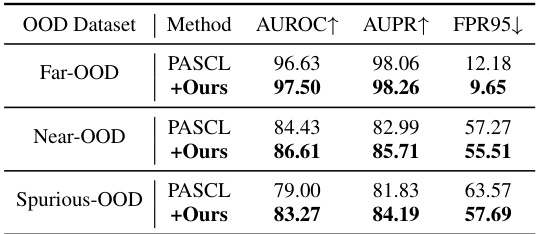
🔼 This table demonstrates the robustness of the proposed method (+Ours) against different OOD test sets, comparing its performance with the baseline method (PASCL) across three types of OOD datasets: Far-OOD, Near-OOD, and Spurious-OOD. The results show consistent improvements in AUROC, AUPR, and FPR95 for the +Ours method across all three OOD types, indicating its generalization capabilities.
read the caption
Table 6: Robustness to OOD test sets.
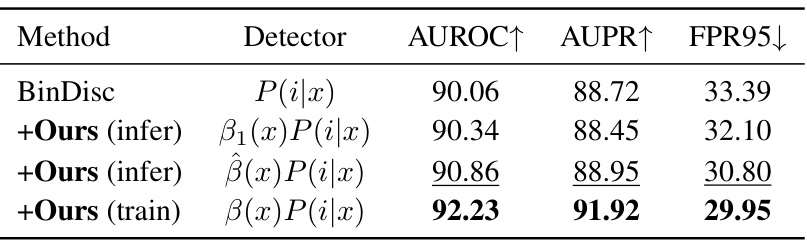
🔼 This table presents the results of applying the ImOOD method during the inference stage of pre-trained models. Three different attempts were made, using different approximations for calculating the bias term β(x). The first attempt uses a constant approximation for β(x). The second utilizes a polynomial to fit the relationship between the predicted class and β(x). The third is the full ImOOD method which involves training. The results show that the full ImOOD method achieves the best performance, demonstrating its effectiveness in improving OOD detection. This table is part of section 4.4 which demonstrates the inference-time application of ImOOD.
read the caption
Table 7: Attempts to apply our ImOOD into pre-trained models' inference stages.
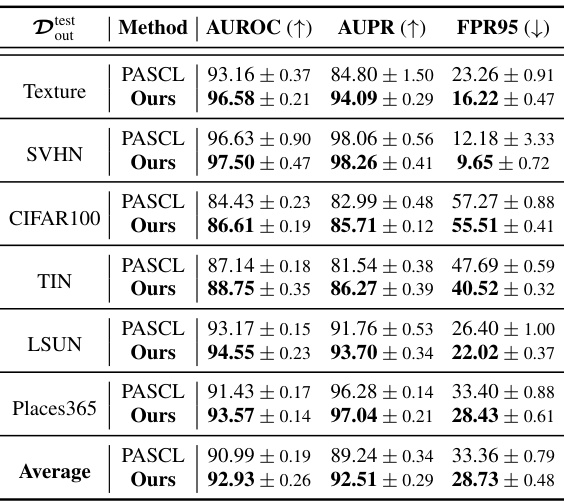
🔼 This table presents the results of out-of-distribution (OOD) detection experiments conducted on the CIFAR10-LT and CIFAR100-LT benchmark datasets. The table compares various OOD detection methods, including the proposed ImOOD method, against state-of-the-art baselines. Results are reported for AUROC (Area Under the Receiver Operating Characteristic curve), AUPR (Area Under the Precision-Recall curve), and FPR95 (False Positive Rate at 95% True Positive Rate). Higher AUROC and AUPR values and lower FPR95 values indicate better performance. The base model used for all methods is ResNet18.
read the caption
Table 1: OOD detection evaluation on CIFAR10/100-LT benchmarks. The best results are marked in bold, and the secondary results are marked with underlines. The base model is ResNet18.
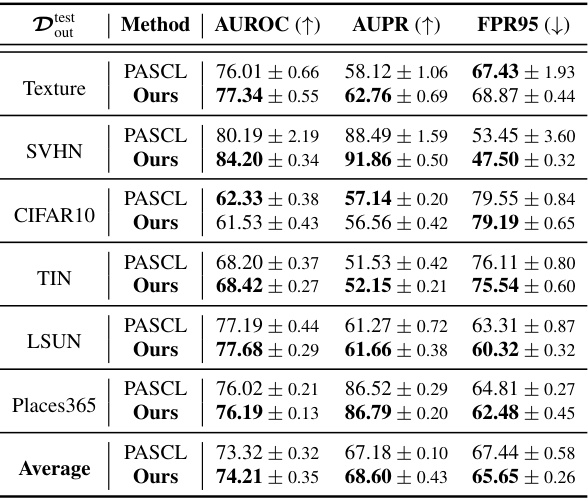
🔼 This table presents the results of OOD detection experiments conducted on the CIFAR10-LT and CIFAR100-LT benchmark datasets. Multiple methods are compared, including baseline methods and the authors’ proposed ImOOD method, both alone and combined with other state-of-the-art techniques like PASCL and COCL. The evaluation metrics used are AUROC (Area Under the Receiver Operating Characteristic curve), AUPR (Area Under the Precision-Recall curve), and FPR95 (False Positive Rate at 95% True Positive Rate). Higher AUROC and AUPR values are better, while a lower FPR95 value is preferred. The table allows for a comparison of the performance of different OOD detection methods in the context of imbalanced data.
read the caption
Table 1: OOD detection evaluation on CIFAR10/100-LT benchmarks. The best results are marked in bold, and the secondary results are marked with underlines. The base model is ResNet18.
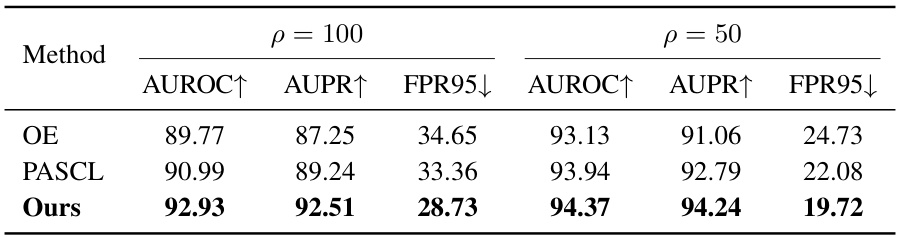
🔼 This table presents the results of OOD detection experiments conducted on the CIFAR10-LT and CIFAR100-LT benchmarks. It compares various methods, including the proposed ImOOD approach, against several state-of-the-art (SOTA) methods. Evaluation metrics (AUROC, AUPR, FPR95) and classification accuracy (ACC) are reported. The base model used across all methods is ResNet18. Bold values represent the best performing method for each metric, while underlined values indicate the second-best performance. The table highlights the superior performance of the ImOOD method in comparison to existing techniques.
read the caption
Table 1: OOD detection evaluation on CIFAR10/100-LT benchmarks. The best results are marked in bold, and the secondary results are marked with underlines. The base model is ResNet18.
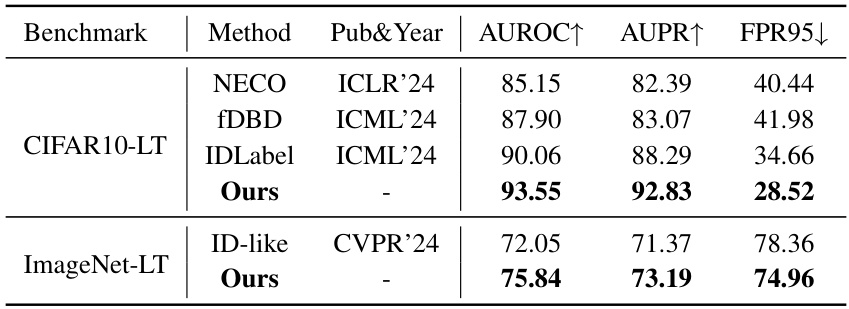
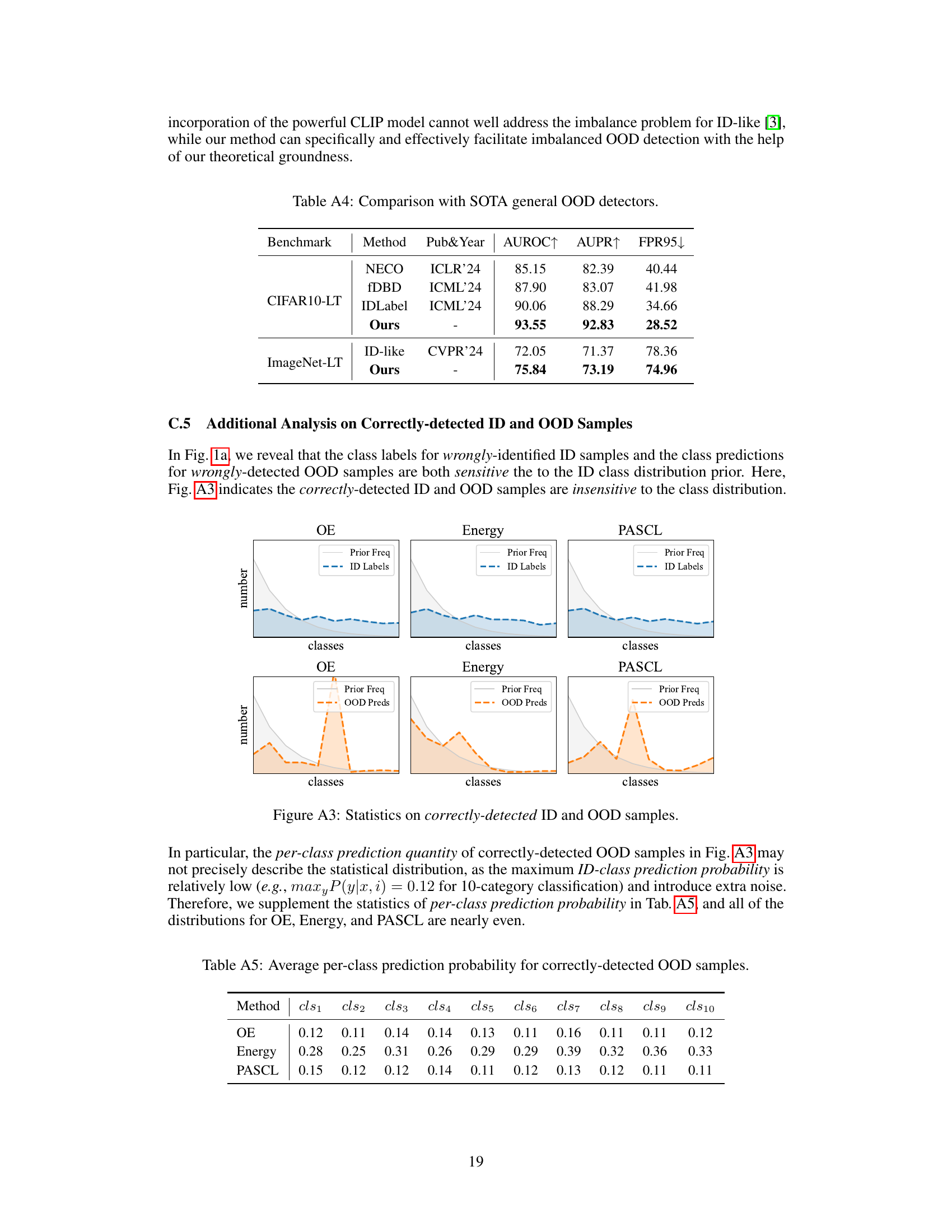
🔼 This table compares the proposed ImOOD method with several state-of-the-art general out-of-distribution (OOD) detection methods on the CIFAR10-LT and ImageNet-LT benchmarks. The results are presented in terms of AUROC (Area Under the Receiver Operating Characteristic curve), AUPR (Area Under the Precision-Recall curve), and FPR95 (False Positive Rate at 95% true positive rate). ImOOD demonstrates superior performance compared to existing methods, highlighting its effectiveness.
read the caption
Table 4: Comparison with SOTA general OOD detectors.

🔼 This table presents the average prediction probability for each of the ten classes (cls1 to cls10) when evaluating the performance of three different Out-of-Distribution (OOD) detection methods: OE, Energy, and PASCL. The values represent the average probability assigned to each class for correctly identified OOD samples. The purpose is to show the distribution of these probabilities across classes for each method and to highlight whether the methods show any class bias in their OOD detection.
read the caption
Table A5: Average per-class prediction probability for correctly-detected OOD samples.
Full paper#