TL;DR#
Current methods for evaluating generative models often depend on reference datasets, which are not always available and can be computationally expensive to use for large models. This paper addresses the issue of computationally expensive and reference-dependent diversity evaluation of generative models.
FKEA, a novel method, leverages random Fourier features to efficiently approximate kernel entropy scores (VENDI and RKE), achieving O(n) complexity which scales linearly. This allows for evaluating diversity in large-scale models on standard datasets (image, text, and video), without needing reference datasets, and its interpretability is demonstrated through visualizing identified modes. The proposed method outperforms baseline methods in terms of scalability.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in generative models because it introduces a scalable and interpretable method for evaluating model diversity without relying on reference datasets, a significant limitation of existing methods. This opens new avenues for research on large-scale models and improves our ability to compare models in scenarios where reference data is scarce or unavailable.
Visual Insights#

🔼 This figure compares reference-based and reference-free evaluation metrics for Stable Diffusion XL-generated elephant images. Two datasets are shown: one with ‘regular’ elephants and one with colored elephants. Reference-based metrics (FID, Recall, Coverage) use ImageNet’s Indian elephant images as a reference, while reference-free metrics (VENDI, RKE) assess diversity without a reference set. The figure demonstrates a discrepancy between reference-based and reference-free scores, particularly in the colored elephant dataset where reference-free metrics show substantially higher diversity despite comparable reference-based scores.
read the caption
Figure 1: Reference-based vs. reference-free scores on two datasets of Stable Diffusion XL generated elephant images. FID, Recall, and Coverage scores (colored orange) are reference-based, whereas VENDI and RKE scores (colored blue) are reference-free. Inception.V3 is used as the backbone embedding. Reference-based metrics use 'Indian elephant' samples in ImageNet as reference data.

🔼 This table compares the computational time (in seconds) required to calculate FKEA-RKE, FKEA-VENDI, RKE, and VENDI scores on the ImageNet dataset using DinoV2 embeddings for various sample sizes (n). The results are shown for two different random Fourier feature dimensions (2r = 8000 and 2r = 16000). The table highlights the scalability of the FKEA method in comparison to the conventional RKE and VENDI approaches, particularly for larger datasets, due to memory constraints. Note that RKE and VENDI calculations were not performed for sample sizes exceeding 40,000.
read the caption
Table 1: Time complexity for FKEA and non-FKEA based metrics (RKE and VENDI) on ImageNet dataset with DinoV2 embedding. Computation of VENDI and RKE on 40k+ samples are omitted due to memory overflow during metric computation.
In-depth insights#
Ref-Free Eval#
The heading ‘Ref-Free Eval’ likely refers to a section discussing reference-free evaluation methods for generative models. Standard evaluation metrics often rely on comparing generated samples to a reference dataset, which can be problematic when a suitable reference is unavailable or when assessing specific aspects beyond simple fidelity. This section likely explores alternative approaches, possibly focusing on intrinsic properties of the generated data such as diversity or representational capacity. It might delve into methods for quantifying these properties without external reference, perhaps using techniques from information theory (entropy estimation) or analyzing the internal structure of the generated data (manifold learning). The discussion would likely cover the advantages of reference-free evaluation – increased generalizability and applicability – but also address any limitations, such as potential biases or sensitivity to the specific evaluation method. The goal is to provide a more objective and robust way to measure the quality of generative models, particularly in scenarios where reference datasets are lacking or inadequate.
FKEA Method#
The core of this research paper centers around the Fourier-based Kernel Entropy Approximation (FKEA) method, a novel approach designed to efficiently and scalably evaluate generative models without relying on reference datasets. FKEA cleverly leverages the random Fourier features framework to significantly reduce the computational cost associated with calculating reference-free entropy scores like VENDI and RKE, which are traditionally computationally expensive for large-scale models. This efficiency is achieved by approximating the kernel covariance matrix using random Fourier features, thus enabling the estimation of eigenvalues and, consequently, entropy scores, with a complexity that scales linearly with the sample size (O(n)). Furthermore, FKEA’s application extends to revealing the identified modes of the generative model through analysis of the proxy eigenvectors, offering valuable insights into the diversity of generated samples. The method’s scalability and interpretability are empirically validated, demonstrating its effectiveness across various datasets (image, text, video), making it a promising tool for the evaluation of large-scale generative models. However, limitations such as the reliance on shift-invariant kernels need further consideration.
Scalability#
The paper’s core contribution revolves around enhancing the scalability of reference-free generative model evaluation. Existing methods, while offering the advantage of reference independence, suffer from significant computational limitations, particularly when dealing with large datasets. The authors address this crucial issue by leveraging the Random Fourier Features (RFF) framework to develop the Fourier-based Kernel Entropy Approximation (FKEA) method. This approach drastically reduces the computational complexity, enabling efficient evaluation of even substantial datasets and models. FKEA achieves linear scaling with the sample size, a significant improvement over the quadratic complexity of prior reference-free approaches. This enhanced scalability is a key strength, allowing researchers to assess the quality and diversity of generative models in large-scale applications where previously infeasible. The empirical results across various image, text, and video datasets robustly demonstrate the practicality and efficacy of FKEA in large-scale settings.
Limitations#
The heading ‘Limitations’ in a research paper serves a crucial role in acknowledging the boundaries of the study. A thoughtful limitations section demonstrates intellectual honesty and strengthens the paper’s credibility. It should address aspects like methodological constraints, such as the choice of specific algorithms or datasets impacting generalizability. Computational limitations, especially concerning scalability to larger datasets or complex models, are also significant. The discussion should explicitly mention any assumptions made, and how those assumptions could limit the findings. Generalizability is key—does the analysis apply to various datasets, generative models, or domains? Addressing these questions transparently enhances the overall impact and reliability of the research. A well-written limitations section does not detract from the work; instead, it enhances its value by offering a balanced perspective.
Future Work#
The paper’s lack of a dedicated ‘Future Work’ section presents an opportunity for insightful expansion. Future research could investigate the applicability of FKEA to a wider range of kernels, moving beyond shift-invariant kernels to encompass more versatile options used in various machine learning applications. A thorough analysis of the impact of different embedding spaces on FKEA’s performance is warranted. The robustness and sensitivity of the method to variations in embedding choice need further exploration. Investigating the theoretical sample complexity of FKEA, particularly in high-dimensional spaces, is crucial for establishing more rigorous guarantees. This would provide deeper insight into the method’s reliability and scalability. Finally, extending FKEA’s capabilities to address the challenges of text and video data diversity evaluation more directly would significantly broaden its impact and practical relevance within the field of generative model analysis.
More visual insights#
More on figures
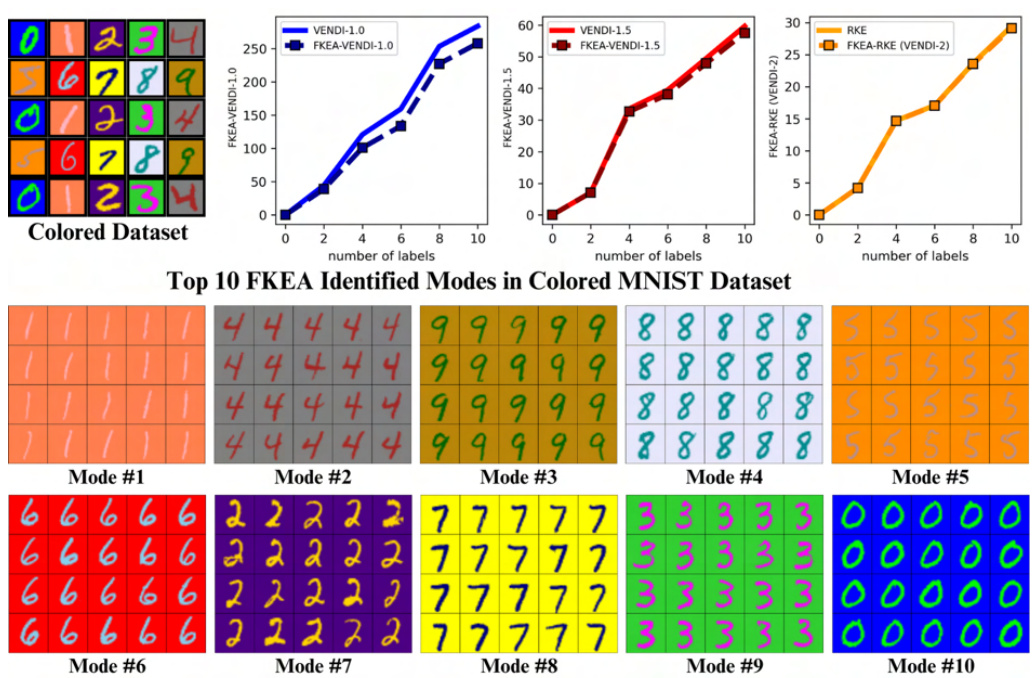
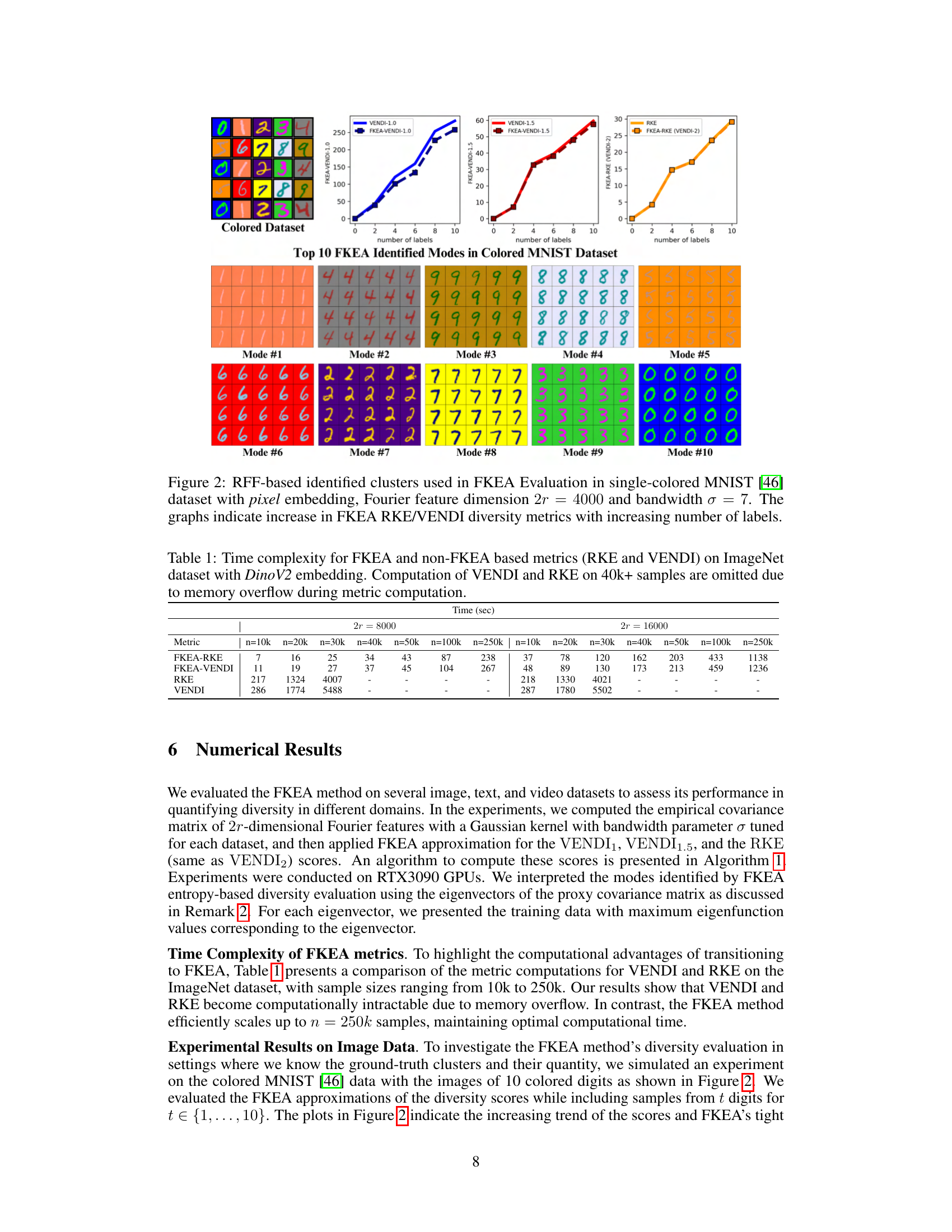
🔼 This figure shows the top 10 modes identified by FKEA in a single-colored MNIST dataset. Each mode represents a cluster of similar images. The plots show how the reference-free diversity metrics (RKE and VENDI) increase as the number of labels (i.e., the number of distinct digit classes present in the generated samples) increases. The images in each mode illustrate the types of digits that are grouped together by the algorithm.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.
🔼 This figure demonstrates the results of applying the Fourier-based Kernel Entropy Approximation (FKEA) method to the single-colored MNIST dataset. The method identifies clusters within the data based on the eigenvectors of a proxy kernel matrix calculated using random Fourier features. The figure shows the top 10 identified clusters (modes) and plots showing how the FKEA-based RKE and VENDI diversity metrics increase with the number of labels (classes) in the dataset. This illustrates the scalability and interpretability of FKEA in evaluating the diversity of generated samples.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.
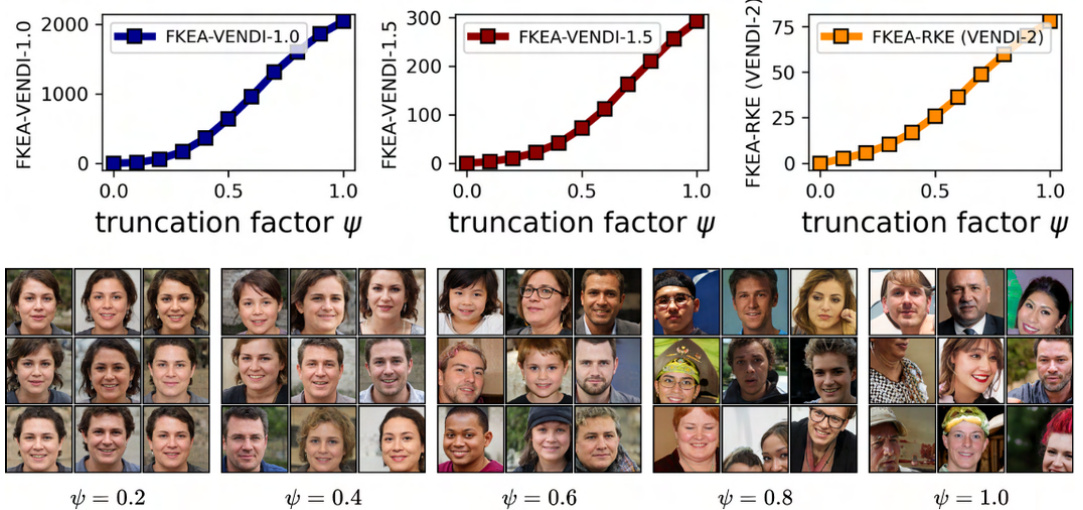
🔼 This figure shows how FKEA metrics (FKEA-VENDI-1.0, FKEA-VENDI-1.5, and FKEA-RKE) change with different truncation factors (ψ) applied to StyleGAN3 generated FFHQ samples. The plots illustrate the increasing trend of the scores with increasing truncation factor values, indicating how this parameter affects the diversity assessment by FKEA. The image grids below the plots show samples from the top clusters with the highest scores for each truncation factor, giving a visual representation of the clustering behavior.
read the caption
Figure 4: FKEA metrics behavior under different truncation factor ψ of StyleGAN3 [47] generated FFHQ samples.
🔼 This figure visualizes the clusters identified by the Fourier-based Kernel Entropy Approximation (FKEA) method in a single-colored version of the MNIST dataset. The FKEA method uses random Fourier features to approximate the kernel matrix, making it computationally efficient for large datasets. The plots in the figure show the increase in the RKE and VENDI diversity metrics as the number of labels increases. The identified modes, or clusters, are visually represented, demonstrating how FKEA groups similar images together.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.

🔼 This figure shows the top 10 modes identified by the FKEA method in a single-colored MNIST dataset. Each mode represents a cluster of similar images. The RFF (Random Fourier Features) method was used with 4000 features and a bandwidth of 7. As the number of labels (representing different digits) increases, the diversity metrics (RKE and VENDI) also increase, indicating that the model generates more diverse images.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.

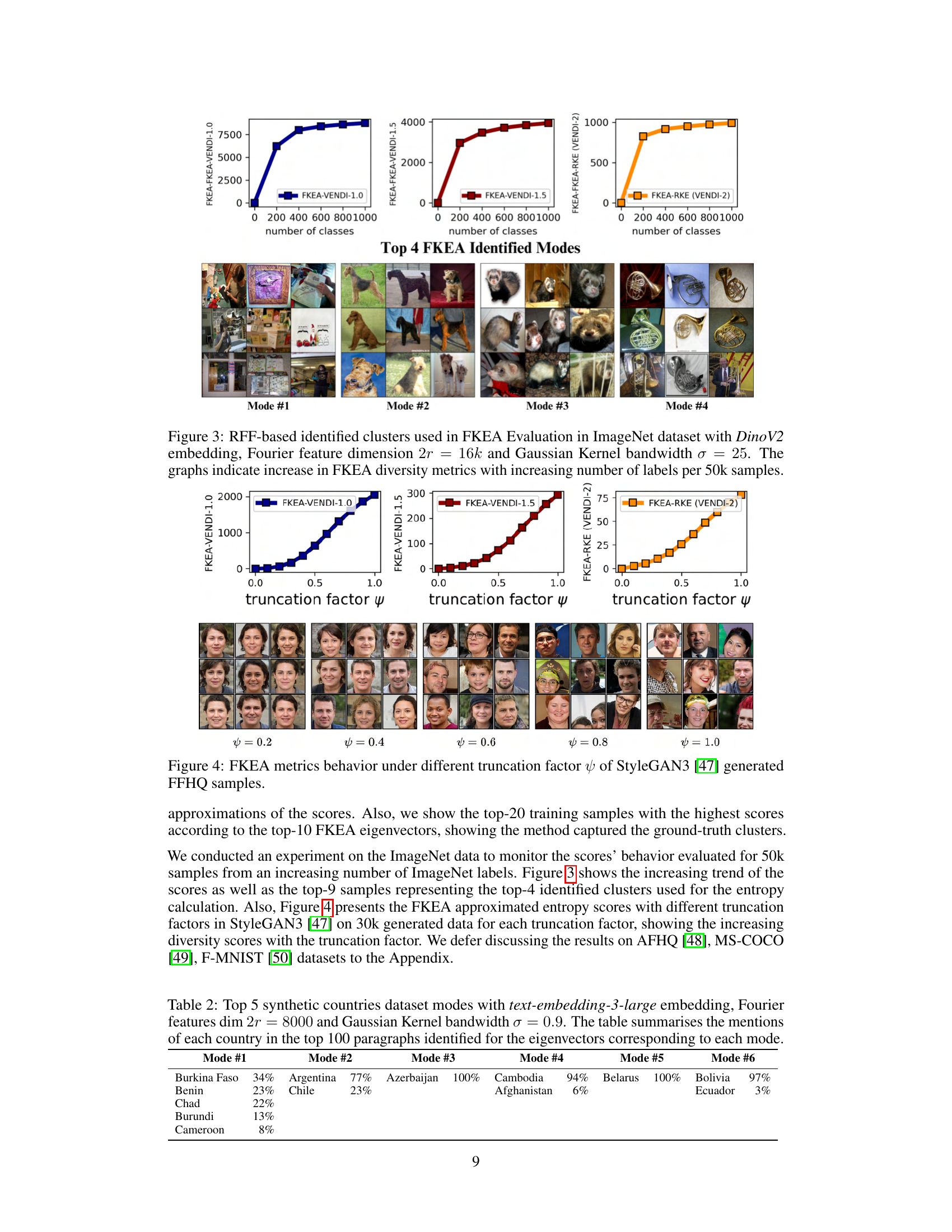
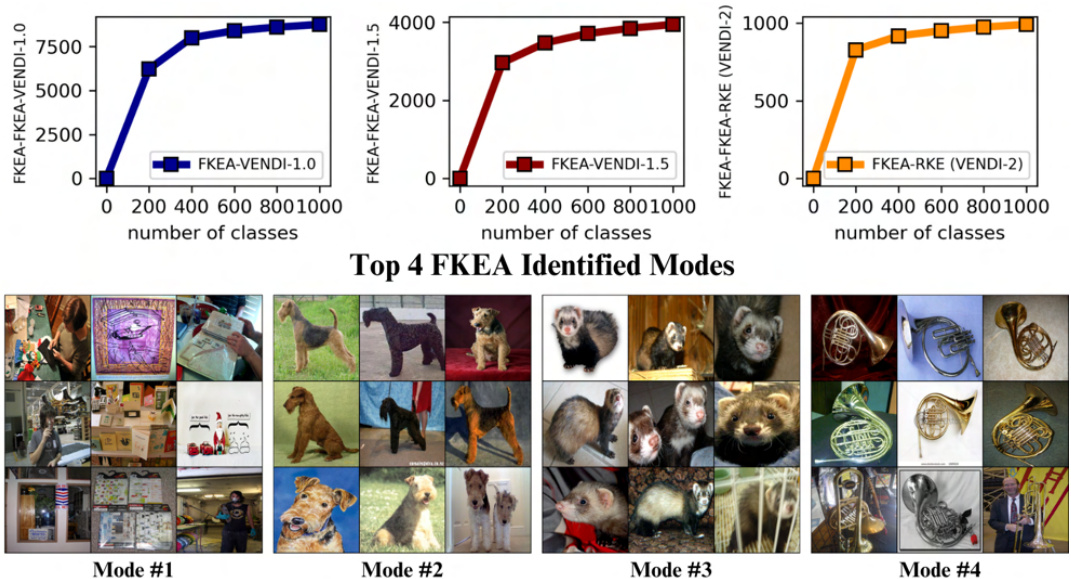
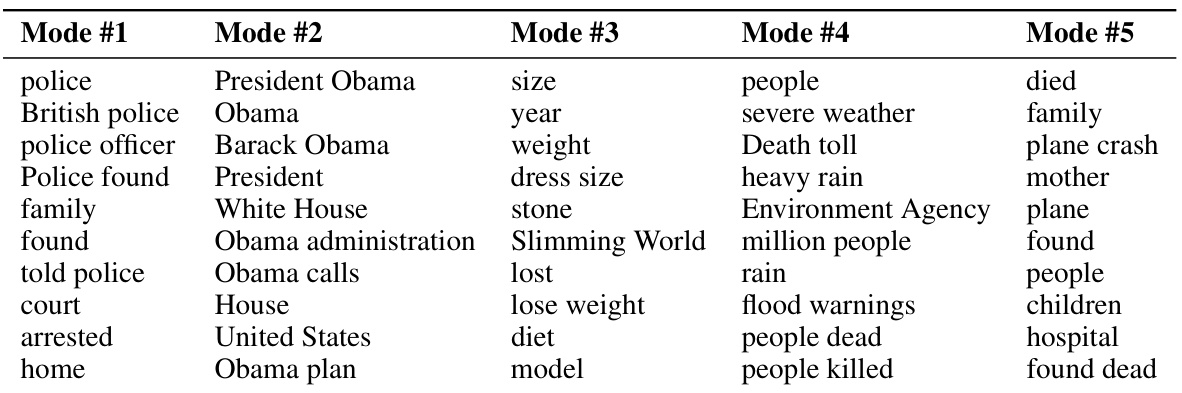
🔼 This figure shows the top 4 clusters identified by the Fourier-based Kernel Entropy Approximation (FKEA) method on the ImageNet dataset using DinoV2 embeddings and a Gaussian kernel with bandwidth σ = 25. The results are displayed for four different sample sizes: 10k, 50k, 100k, and 250k. The images within each cluster visually represent the types of images that are grouped together by the algorithm. As the number of samples increases, the clusters become more coherent and the algorithm’s ability to group similar images improves, demonstrating the scalability of the FKEA method.
read the caption
Figure 7: RFF-based identified clusters used in FKEA Evaluation in ImageNet dataset with DinoV2 embeddings and bandwidth σ = 25 at varying number of samples n

🔼 This figure visualizes the top 10 modes identified by the Fourier-based Kernel Entropy Approximation (FKEA) method in a single-colored MNIST dataset. It shows how the FKEA method identifies clusters of similar images (modes), and demonstrates that the diversity metrics (RKE and VENDI) increase as the number of distinct image classes (labels) in the dataset grows. Each mode displays a representative set of images belonging to that specific cluster, highlighting the method’s ability to capture and quantify the diversity of generated samples.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.

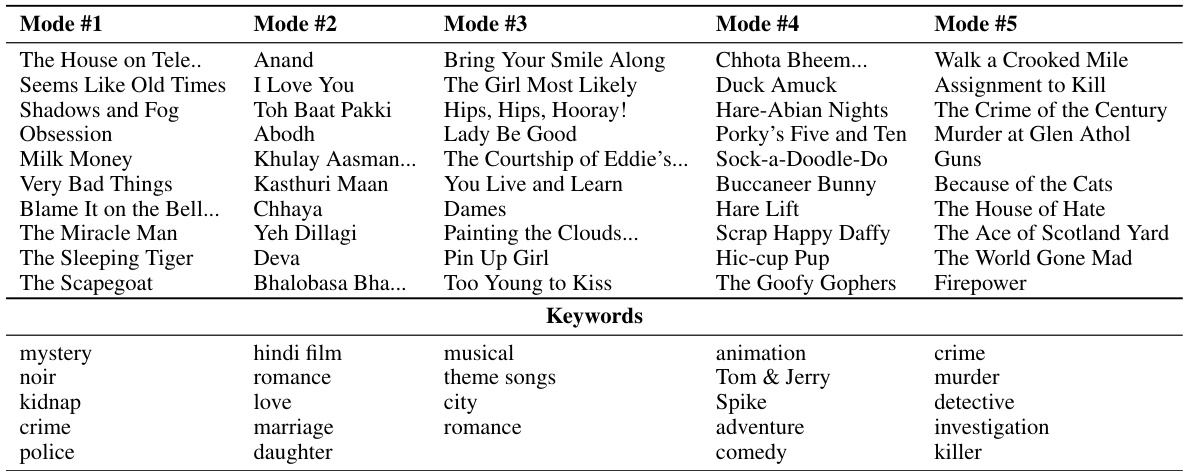
🔼 This figure shows the top 8 clusters identified by the Fourier-based Kernel Entropy Approximation (FKEA) method in the FFHQ dataset. The FKEA method uses random Fourier features to efficiently approximate the kernel covariance matrix, enabling scalable evaluation of generative models. Each cluster represents a mode identified by FKEA and showcases a set of images belonging to that mode. The images illustrate the diversity of generated samples that fall into each of the identified clusters in the FFHQ dataset. DinoV2 embeddings and a bandwidth (σ) of 20 were used in the FKEA evaluation.
read the caption
Figure 8: RFF-based identified clusters used in FKEA Evaluation in FFHQ dataset with DinoV2 embeddings and bandwidth σ = 20

🔼 This figure shows the top 10 modes identified by FKEA in a single-colored MNIST dataset. Each mode represents a cluster of similar images. The graphs illustrate how the RKE and VENDI diversity scores increase as the number of distinct digit labels in the dataset grows, demonstrating that FKEA can effectively capture and quantify the diversity of generated data.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.

🔼 This figure shows the top 4 modes identified by FKEA in the ImageNet dataset using DinoV2 embeddings and a Gaussian kernel with bandwidth σ = 25. Each mode represents a cluster of images with similar visual characteristics. The figure demonstrates the effect of the number of samples (n) on the quality and distinctness of these clusters, illustrating improved cluster separation with larger sample sizes.
read the caption
Figure 7: RFF-based identified clusters used in FKEA Evaluation in ImageNet dataset with DinoV2 embeddings and bandwidth σ = 25 at varying number of samples n

🔼 This figure shows the top 8 clusters identified by the Fourier-based Kernel Entropy Approximation (FKEA) method on the Fashion-MNIST dataset. Each cluster represents a distinct mode identified by FKEA, visually demonstrating the diversity of the generated samples according to the method. The use of pixel embeddings and a bandwidth (σ) of 15 are specified parameters of the FKEA process for this dataset.
read the caption
Figure 11: RFF-based identified clusters used in FKEA Evaluation in FASHION-MNIST [50] dataset with pixel embeddings and bandwidth σ = 15.

🔼 This figure shows the top 10 modes identified by FKEA in a single-colored MNIST dataset. Each mode represents a cluster of similar images. The figure demonstrates that as the number of labels (i.e., the number of distinct digit classes considered) increases, the FKEA-based RKE and VENDI diversity scores also increase, indicating that the model generates more diverse samples. The visualizations help illustrate how FKEA identifies modes (clusters) in the data.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.

🔼 This figure visualizes the top 10 modes identified by the Fourier-based Kernel Entropy Approximation (FKEA) method on a single-colored version of the MNIST dataset. The visualization shows the identified image clusters for each mode, indicating that FKEA captures distinct visual patterns. The accompanying plots illustrate a trend of increasing diversity metrics (RKE and VENDI) as the number of labels increases, suggesting that FKEA effectively captures the diversity of the generated data. Pixel embeddings were used, along with a Fourier feature dimension of 4000 and a bandwidth of 7.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.

🔼 This figure shows the top 10 modes identified by FKEA in the colored MNIST dataset. Each mode represents a cluster of similar images. The number of labels increases from 2 to 10, showing how the diversity metrics (RKE and VENDI) increase with the number of distinct clusters.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.

🔼 This figure shows the top 10 modes identified by the FKEA method in a single-colored MNIST dataset. Each mode represents a cluster of similar images, and the figure demonstrates how the diversity metrics (RKE and VENDI) increase as the number of distinct image classes (labels) increases. The results visually showcase how the FKEA method successfully identifies and separates distinct clusters of images based on visual characteristics.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.

🔼 This figure shows the top 4 modes identified by FKEA in the ImageNet dataset using DinoV2 embeddings and a Gaussian kernel with a bandwidth of 25. It demonstrates how the quality of the identified clusters improves as the number of samples (n) increases, progressing from noisy and merged clusters at n=10k to more coherent and meaningful clusters at n=250k. This highlights the importance of sample size for accurate entropy estimation using FKEA.
read the caption
Figure 7: RFF-based identified clusters used in FKEA Evaluation in ImageNet dataset with DinoV2 embeddings and bandwidth σ = 25 at varying number of samples n.

🔼 This figure shows the top 4 modes identified by the FKEA method in the ImageNet dataset using DinoV2 embeddings and a Gaussian kernel with bandwidth σ = 25. It demonstrates the impact of the number of samples (n) on the quality and coherence of the resulting clusters. As the number of samples increases from 10k to 250k, the clusters become increasingly refined and semantically meaningful, highlighting the scalability of the FKEA approach for large datasets.
read the caption
Figure 7: RFF-based identified clusters used in FKEA Evaluation in ImageNet dataset with DinoV2 embeddings and bandwidth σ = 25 at varying number of samples n

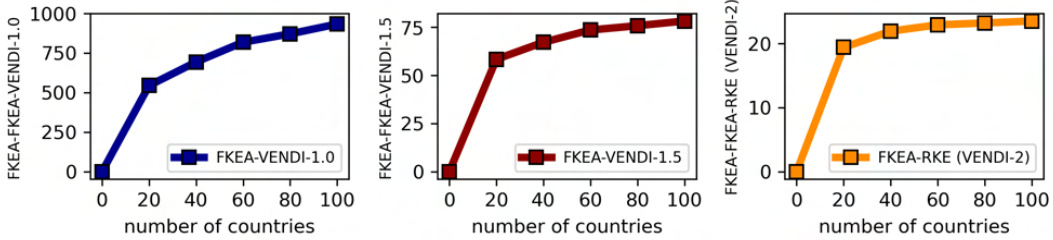
🔼 This figure displays the convergence behavior of diversity metrics (VENDI and RKE, both with and without FKEA approximation) across various text and image embeddings. The left panels show results for different text embeddings (text-embedding-3-large, text-embedding-3-small, Gemini, BERT) on a synthetic dataset with an increasing number of countries. The right panels showcase similar results for different image embeddings (DinoV2, CLIP, InceptionV3, SwAV) on the ImageNet dataset with an increasing number of classes. The plots illustrate how the diversity metrics evolve as the number of data samples increases, demonstrating the convergence properties of the FKEA method.
read the caption
Figure 19: Summary of diversity convergence with r = 12000 and sample size n = 20000.
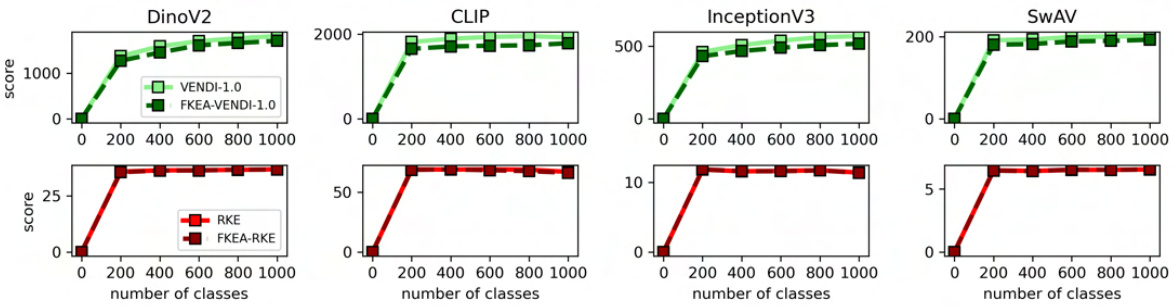
🔼 This figure displays the convergence behavior of diversity metrics (VENDI-1.0, FKEA-VENDI-1.0, RKE, and FKEA-RKE) across different embedding spaces (DinoV2, CLIP, InceptionV3, and SwAV) and datasets (synthetic countries and ImageNet). The x-axis represents the number of classes, while the y-axis shows the diversity score. The plots illustrate how the diversity scores converge as the number of classes increases, demonstrating the scalability of FKEA across various embedding spaces and datasets.
read the caption
Figure 19: Summary of diversity convergence with r = 12000 and sample size n = 20000.

🔼 This figure shows the results of applying the Fourier-based Kernel Entropy Approximation (FKEA) method to the single-colored MNIST dataset. The FKEA method identifies clusters within the data and calculates diversity scores (RKE and VENDI). The graphs demonstrate that as the number of labels (classes) increases, so does the diversity, indicating that the FKEA method effectively captures the diversity of generated data.
read the caption
Figure 2: RFF-based identified clusters used in FKEA Evaluation in single-colored MNIST [46] dataset with pixel embedding, Fourier feature dimension 2r = 4000 and bandwidth σ = 7. The graphs indicate increase in FKEA RKE/VENDI diversity metrics with increasing number of labels.
More on tables

🔼 This table compares the computation time of FKEA and non-FKEA based methods (RKE, VENDI) on the ImageNet dataset. It uses DinoV2 embeddings and shows how the time scales with increasing sample size (n). Note that VENDI and RKE computations were not performed for sample sizes above 40,000 due to memory limitations.
read the caption
Table 1: Time complexity for FKEA and non-FKEA based metrics (RKE and VENDI) on ImageNet dataset with DinoV2 embedding. Computation of VENDI and RKE on 40k+ samples are omitted due to memory overflow during metric computation.
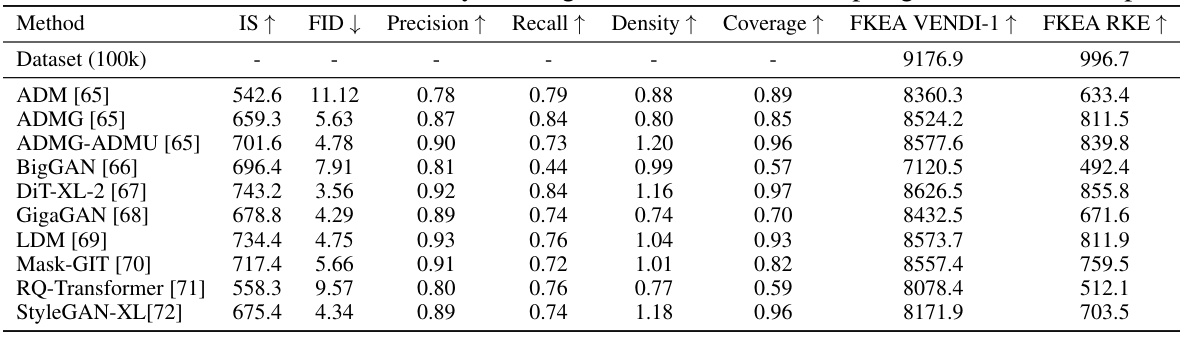
🔼 This table compares the performance of various generative models on the ImageNet dataset using different metrics. It includes both reference-based metrics (IS, FID, Precision, Recall, Density, Coverage) and the proposed reference-free metrics (FKEA VENDI-1, FKEA RKE). The Gaussian kernel bandwidth and Fourier features dimension are specified. The scores are based on 50,000 pre-generated samples.
read the caption
Table 3: Evaluated scores for ImageNet generative models. The Gaussian kernel bandwidth parameter chosen for RKE, VENDI, FKEA-VENDI and FKEA-RKE is σ = 25 and Fourier features dimension 2r = 16k. The scores were obtained by running the GitHub of [20] on pre-generated 50k samples.

🔼 This table compares the computation time of the FKEA method and traditional methods for calculating RKE and VENDI scores on the ImageNet dataset using DinoV2 embeddings. It shows how the FKEA method scales efficiently to large datasets (up to 250k samples), while traditional methods fail due to memory limitations at larger sample sizes.
read the caption
Table 1: Time complexity for FKEA and non-FKEA based metrics (RKE and VENDI) on ImageNet dataset with DinoV2 embedding. Computation of VENDI and RKE on 40k+ samples are omitted due to memory overflow during metric computation.
🔼 This table compares the performance of various generative models on the ImageNet dataset using different diversity metrics. The metrics include Inception Score (IS), Fréchet Inception Distance (FID), Precision, Recall, Density, Coverage, FKEA VENDI-1, and FKEA RKE. The Gaussian kernel bandwidth and Fourier features dimension are specified. Note that the scores were obtained using pre-generated samples.
read the caption
Table 3: Evaluated scores for ImageNet generative models. The Gaussian kernel bandwidth parameter chosen for RKE, VENDI, FKEA-VENDI and FKEA-RKE is σ = 25 and Fourier features dimension 2r = 16k. The scores were obtained by running the GitHub of [20] on pre-generated 50k samples.
🔼 This table compares the computation time of FKEA and traditional RKE/VENDI methods for different sample sizes on the ImageNet dataset. The results highlight FKEA’s scalability advantage, as RKE and VENDI become computationally intractable for larger datasets (above 40,000 samples) due to memory limitations. The table shows the time (in seconds) taken to compute FKEA-RKE, FKEA-VENDI, RKE and VENDI for various sample sizes (10k, 20k, 30k, 40k, 50k, 100k, 250k) and two different Fourier feature dimensions (2r = 8000 and 2r = 16000).
read the caption
Table 1: Time complexity for FKEA and non-FKEA based metrics (RKE and VENDI) on ImageNet dataset with DinoV2 embedding. Computation of VENDI and RKE on 40k+ samples are omitted due to memory overflow during metric computation.
Full paper#