TL;DR#
Time series forecasting is vital across many fields but struggles with real-world data’s noise and anomalies. Existing methods primarily focus on local patterns, neglecting timestamps’ potential for robust global guidance. This leads to inaccurate predictions, particularly when data quality is low.
The proposed GLAFF framework directly addresses this issue by individually modeling timestamps to capture global dependencies. It seamlessly integrates with any existing forecasting model as a “plug-and-play” module, dynamically weighting global and local information for optimal performance. GLAFF significantly improves average forecasting accuracy (12.5%), exceeding state-of-the-art methods (5.5%) across diverse real-world datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in time series forecasting as it introduces a novel framework, GLAFF, that significantly enhances the robustness and accuracy of existing models by effectively utilizing timestamp information. It addresses the limitations of current methods, which often underutilize timestamps, resulting in improved predictive capabilities especially with noisy real-world data. The model-agnostic and plug-and-play nature of GLAFF makes it easily adaptable to various forecasting models, opening new avenues for research and application.
Visual Insights#

🔼 This figure presents the results of an ablation study conducted on the Traffic dataset. It compares the performance of mainstream forecasting models (Informer, TimesNet, iTransformer, DLinear) with and without timestamps. Subfigure (a) shows the MAE and MSE for each model, demonstrating that GLAFF significantly improves performance. Subfigure (b) displays visualizations of actual traffic volume, successful prediction using GLAFF, and a failed prediction (without GLAFF) to highlight the model’s robustness improvements.
read the caption
Figure 1: The experimental results on Traffic dataset. (a) illustrates the outcomes of the ablation study on mainstream forecasting models and their variants. (b) depicts the visualization of traffic volume (upper), successful prediction case (lower right), and failed prediction case (lower left), respectively.
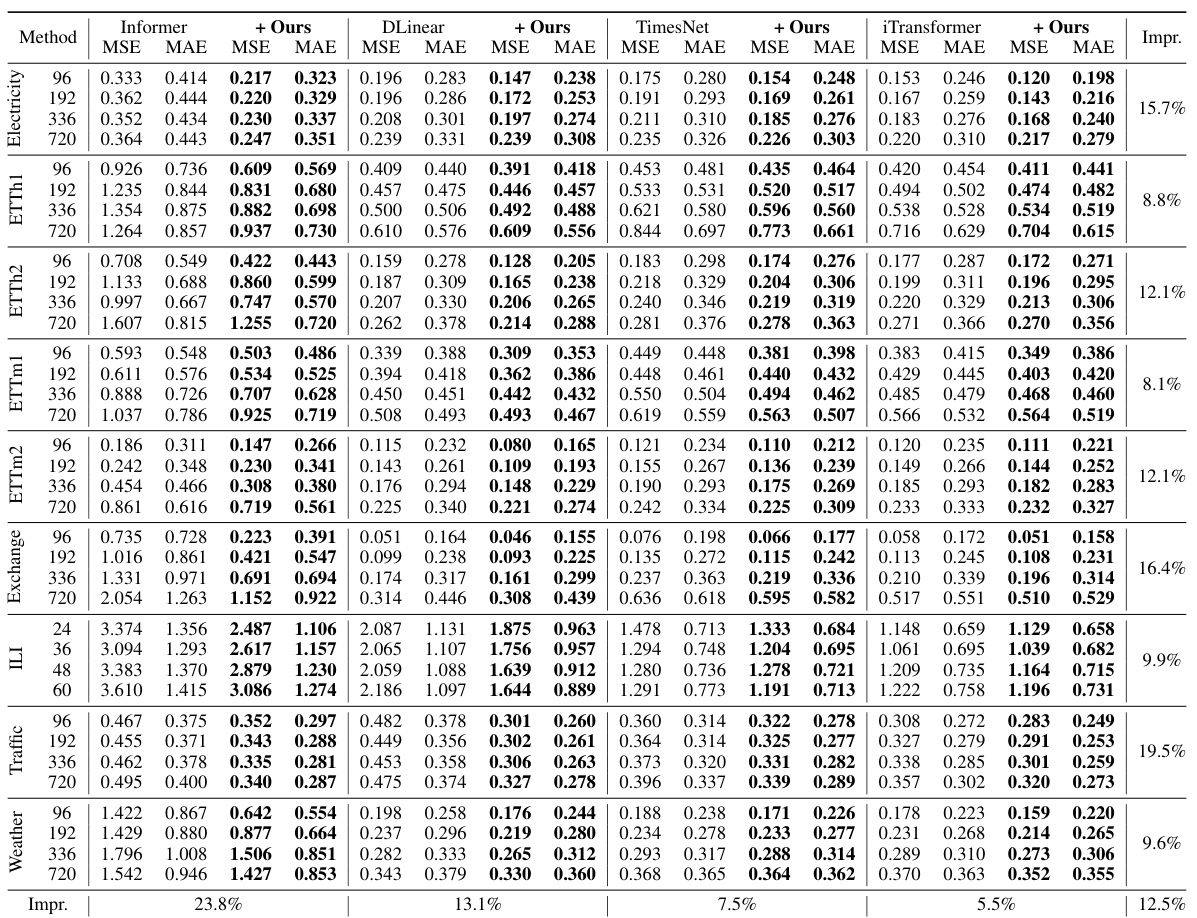
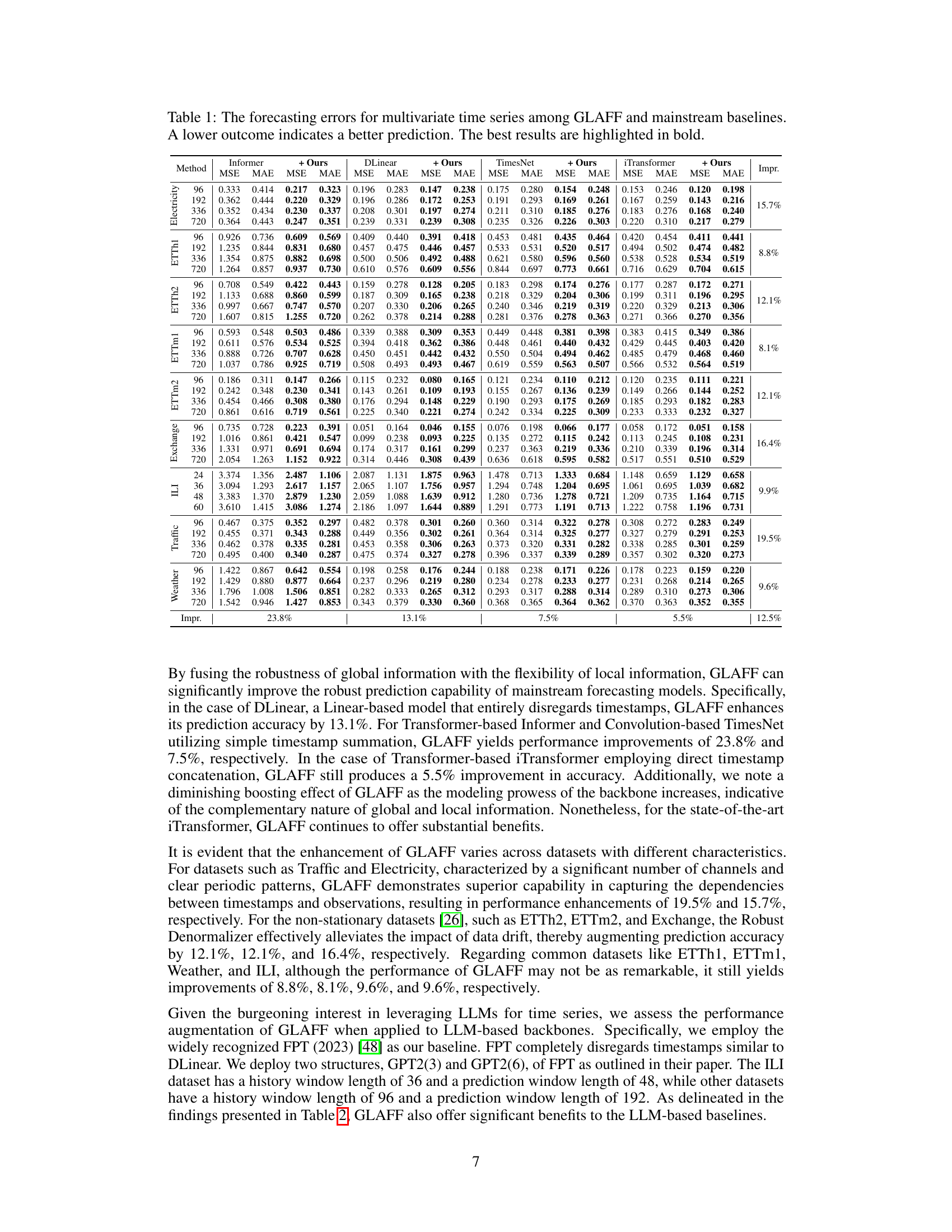
🔼 This table presents the Mean Absolute Error (MAE) and Mean Squared Error (MSE) for nine different multivariate time series datasets using four different forecasting models (Informer, DLinear, TimesNet, iTransformer) and their variants that incorporate GLAFF. Lower values indicate better performance. The table shows the improvement in prediction accuracy achieved by adding GLAFF to each of the base forecasting models across various prediction lengths. The best results for each dataset and prediction length are highlighted in bold.
read the caption
Table 1: The forecasting errors for multivariate time series among GLAFF and mainstream baselines. A lower outcome indicates a better prediction. The best results are highlighted in bold.
In-depth insights#
Timestamp Fusion#
Timestamp fusion in time series forecasting is a crucial technique that leverages the inherent temporal information encoded in timestamps to improve prediction accuracy. Effective fusion strategies combine timestamp features with other time series data to capture both global temporal patterns and local trends. This approach addresses limitations of methods solely relying on local patterns, especially for datasets with noise or anomalies. There are various timestamp fusion methods such as concatenation, summation, or attention-based mechanisms. The choice of method depends on the specific characteristics of the time series data and the forecasting model. A well-designed fusion strategy should handle irregular or missing timestamps, and should adapt to variations in data distribution. The ultimate goal is to enhance the robustness and accuracy of time series forecasts by providing a comprehensive view of temporal information. Successfully integrating timestamps can significantly boost performance, especially in challenging scenarios.
GLAFF Framework#
The GLAFF framework presents a novel approach to robust time series forecasting by fusing global and local information. Its core innovation lies in explicitly leveraging timestamps, often underutilized, to provide robust global guidance. Unlike methods that simply embed timestamps, GLAFF models them individually to capture global dependencies, acting as a plugin adaptable to various forecasting backbones. The framework’s adaptive mechanism seamlessly combines global and local information, adjusting weights dynamically based on data characteristics. This adaptability makes GLAFF particularly effective when dealing with real-world data, which often contains anomalies. Through attention-based mapping and robust denormalization, it handles data drift and anomalies effectively. Extensive empirical evaluation demonstrates significant performance gains across diverse datasets, highlighting GLAFF’s robustness and generalizability.
Robust Forecasting#
Robust forecasting methods are crucial for reliable predictions, especially when dealing with noisy or incomplete data. Traditional forecasting techniques often struggle in such scenarios, leading to inaccurate or unstable results. Robust approaches aim to minimize the impact of outliers and anomalies, ensuring that predictions remain reliable even in the presence of unexpected events. This often involves using statistical methods that are less sensitive to extreme values or employing machine learning models that are specifically trained to handle uncertainty and noise. A key aspect of robust forecasting is model selection and validation. Choosing an appropriate model that is well-suited to the specific characteristics of the data is critical. This includes careful consideration of the data’s underlying distribution and the presence of any seasonality or trends. Effective evaluation metrics are essential for assessing the performance of robust forecasting methods, and these metrics must account for the potential presence of outliers and anomalies. Combining multiple forecasting methods can also enhance robustness by providing a more comprehensive and reliable prediction.
Ablation Study#
An ablation study systematically evaluates the contribution of individual components within a machine learning model. By removing or deactivating one part at a time and observing the impact on overall performance, researchers gain insights into the relative importance of each component. This helps determine which parts are essential for achieving high accuracy and efficiency, and whether simplifying the model by removing less crucial parts is possible without significantly compromising the results. In the context of time series forecasting, an ablation study might involve removing timestamp embeddings, specific attention mechanisms, or data normalization techniques to assess their individual impact on forecasting accuracy. The results highlight the importance of carefully selecting and designing model components, since a poorly chosen component can significantly reduce the model’s predictive capabilities. The findings guide future model development and optimization by indicating which aspects are core to the model’s success and which ones are expendable, leading to more efficient and robust forecasting models.
Future Works#
Future work could explore several promising avenues. Extending GLAFF’s applicability to other time series forecasting backbones beyond the five currently tested is crucial to solidify its model-agnostic nature. Investigating alternative mechanisms for global information fusion, potentially incorporating more sophisticated methods beyond attention mechanisms or exploring hybrid approaches, warrants investigation. The current robust denormalization strategy could benefit from comparative studies against other anomaly handling techniques. Finally, a thorough empirical evaluation on a broader range of real-world datasets with diverse characteristics and noise profiles would strengthen the findings. This comprehensive evaluation should focus on datasets with longer temporal dependencies and scenarios involving substantial data drift.
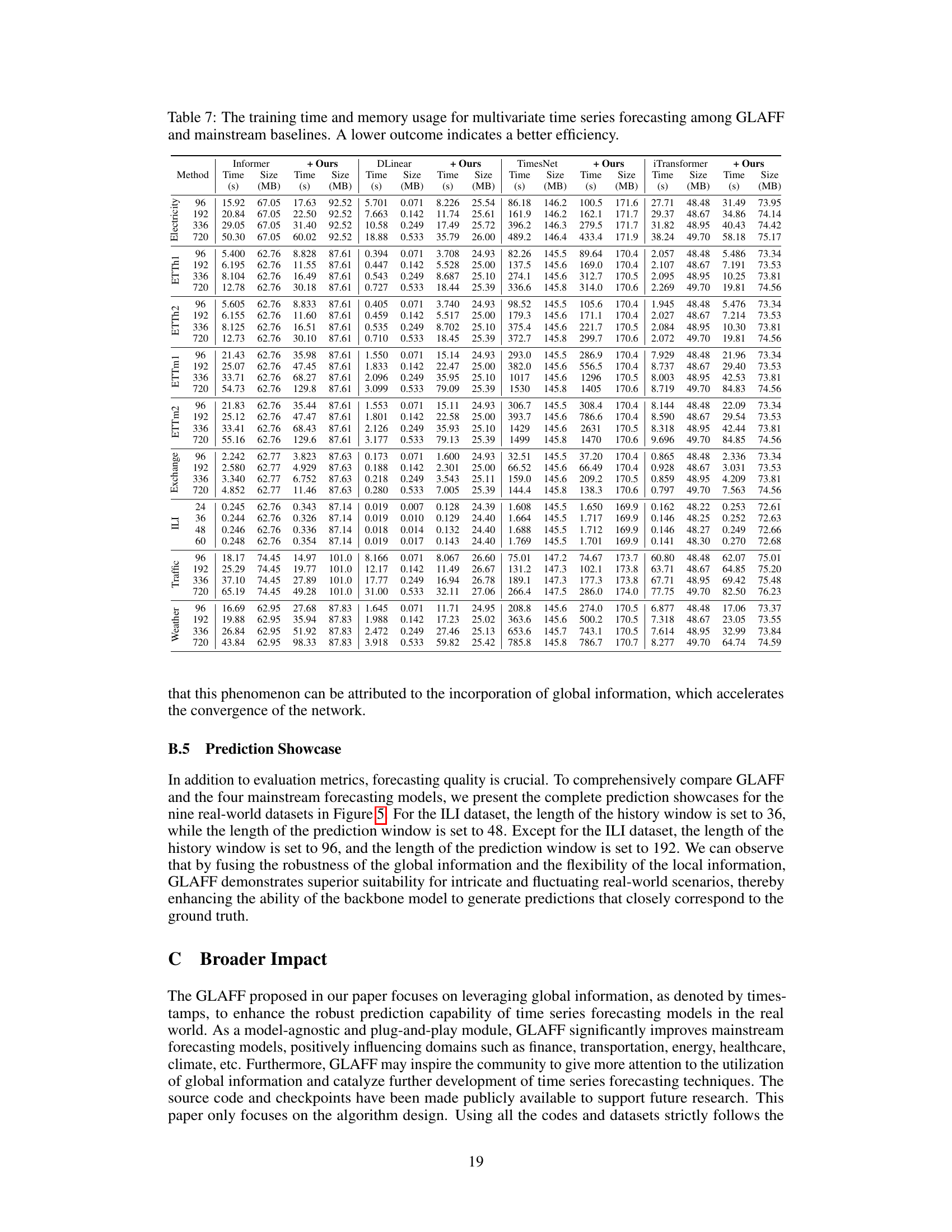
More visual insights#
More on figures

🔼 The figure illustrates the overall architecture of the Global-Local Adaptive Fusion Framework (GLAFF). GLAFF is a plug-and-play module that works with any time series forecasting backbone. It consists of three main parts: 1. Attention-based Mapper: This component processes the timestamps (S and T) to generate global information in the form of initial mappings (X and Y). It uses an attention mechanism to capture dependencies between timestamps. 2. Robust Denormalizer: This component adjusts the initial mappings (X and Y ) to account for data drift by inverse normalizing them to X and Y using quantile deviation. 3. Adaptive Combiner: This component dynamically combines the global information (Y) and the local prediction from the backbone model (Y) to produce the final prediction (Y). The weight of the combination is adjusted based on the difference between the final mapping (X) and the actual observations (X) in the history window. The inputs are the history observations (X), history timestamps (S), future timestamps (T). The output is the prediction (Y).
read the caption
Figure 2: The overall architecture of GLAFF mainly consists of three primary components: Attention-based Mapper, Robust Denormalizer, and Adaptive Combiner.
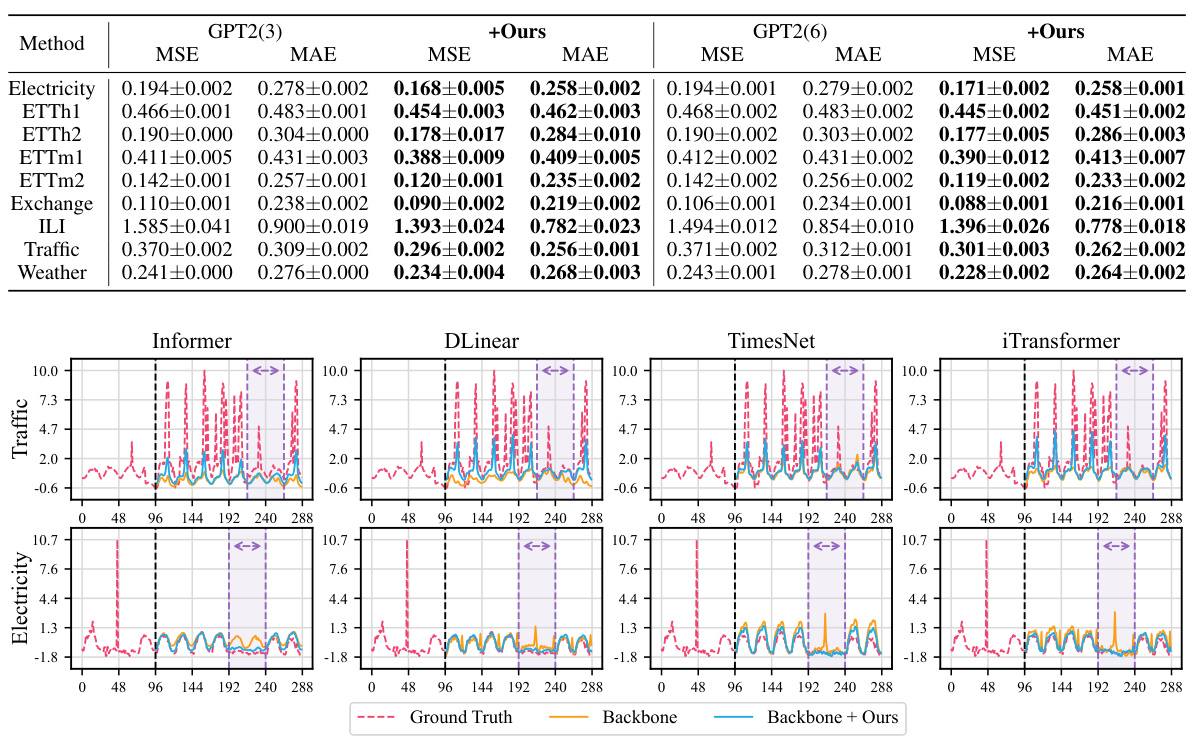
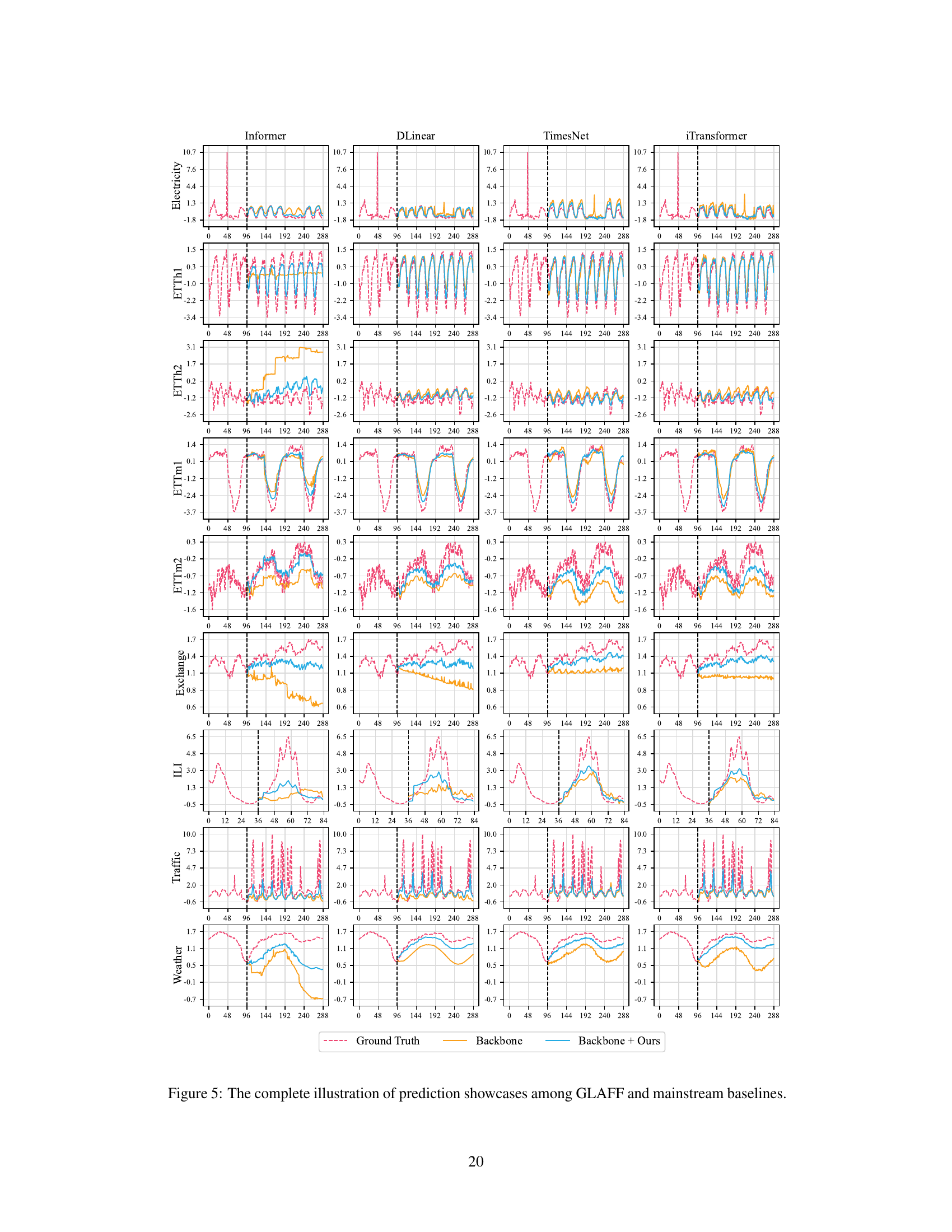
🔼 This figure visualizes the prediction results of four mainstream time series forecasting models (Informer, DLinear, TimesNet, and iTransformer) and their enhanced versions with the proposed GLAFF method on the Traffic and Electricity datasets. It demonstrates the improved prediction accuracy and robustness of GLAFF, especially when handling anomalies in the data (e.g., holidays impacting traffic volume or short circuits affecting electricity consumption). The plots show the ground truth, the predictions from the base models alone, and the predictions from the models enhanced with GLAFF. This allows for a visual comparison of the performance improvements achieved by GLAFF in different scenarios.
read the caption
Figure 3: The illustration of prediction showcases among GLAFF and mainstream baselines.
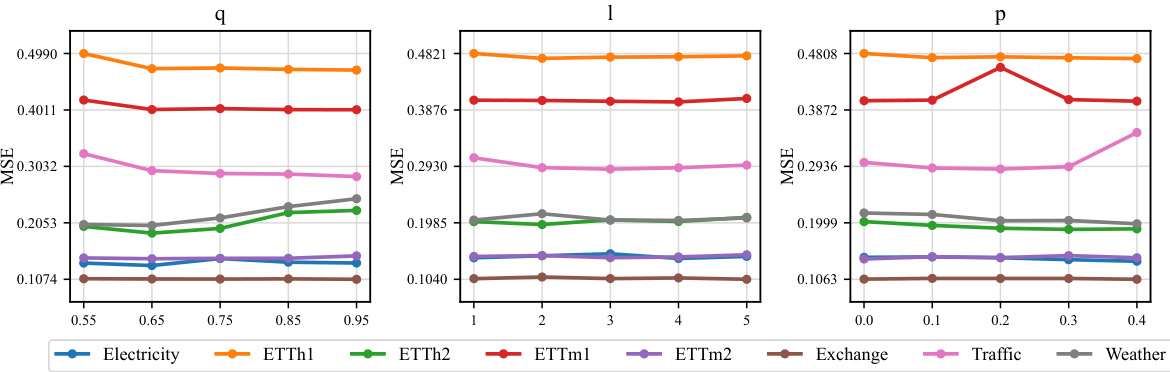
🔼 This figure presents the results of a hyperparameter analysis for the GLAFF model. It shows how different values for the quantile (q) in the Robust Denormalizer, the number of attention blocks (l) in the Attention-based Mapper, and the dropout proportion (p) in the Attention-based Mapper affect the model’s performance, specifically the Mean Squared Error (MSE). The results are shown separately for several datasets to highlight how dataset characteristics influence the effect of each hyperparameter.
read the caption
Figure 4: The forecasting errors for multivariate time series of hyperparameter analysis among different configurations for GLAFF. A lower outcome indicates a better prediction.

🔼 This figure provides a visual comparison of the prediction results from GLAFF and four mainstream time series forecasting models (Informer, DLinear, TimesNet, and iTransformer) across several datasets. The plots show the ground truth values, the predictions made by each baseline model, and the predictions generated after integrating GLAFF into each model. The purpose is to visually demonstrate how GLAFF enhances the performance of the baseline models, particularly in handling anomalies and variations in the time series data.
read the caption
Figure 3: The illustration of prediction showcases among GLAFF and mainstream baselines.
More on tables

🔼 This ablation study analyzes the impact of removing each component of the GLAFF framework on the prediction performance using the iTransformer backbone. It compares the original GLAFF with variants that exclude the backbone, attention mechanism, robust denormalization, or adaptive combiner. The results show the importance of each component and how they contribute to overall performance.
read the caption
Table 3: The forecasting errors for multivariate time series of ablation study among GLAFF and variants. A lower outcome indicates a better prediction. The best results are highlighted in bold.
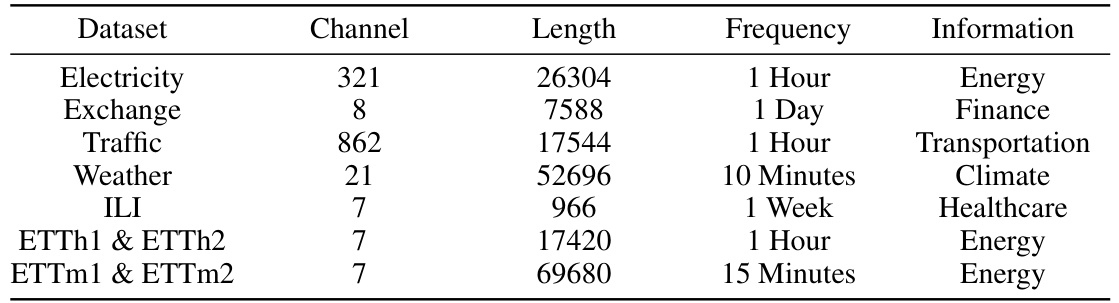
🔼 This table presents a summary of the characteristics of the nine datasets used in the paper’s experiments. For each dataset, it shows the number of channels (variables), the total length of the time series, the frequency of data points (sampling rate), and a brief description of the information contained within the dataset.
read the caption
Table 4: The statistics of each dataset. Channel represents the variate number of each dataset. Length indicates the total number of time points. Frequency denotes the sampling interval of time points.

🔼 This table presents the Mean Squared Error (MSE) and Mean Absolute Error (MAE) for nine different multivariate time series datasets using four common forecasting models (Informer, DLinear, TimesNet, iTransformer) and their versions enhanced with the proposed GLAFF method. Lower MSE and MAE values indicate better forecasting performance. The best results for each dataset and forecasting model are highlighted in bold, demonstrating GLAFF’s improvement in accuracy across various models and datasets.
read the caption
Table 1: The forecasting errors for multivariate time series among GLAFF and mainstream baselines. A lower outcome indicates a better prediction. The best results are highlighted in bold.

🔼 This table presents a comparison of forecasting error metrics (MSE and MAE) for various time series forecasting models (Informer, DLinear, TimesNet, iTransformer) across multiple datasets (Electricity, Exchange, Traffic, Weather, ILI, and four ETT datasets) and with/without the proposed GLAFF framework. The results show the improvement provided by integrating GLAFF with each baseline model.
read the caption
Table 1: The forecasting errors for multivariate time series among GLAFF and mainstream baselines. A lower outcome indicates a better prediction. The best results are highlighted in bold.

🔼 This table presents a comparison of forecasting error metrics (Mean Squared Error (MSE) and Mean Absolute Error (MAE)) for several multivariate time series datasets. The models compared are several mainstream forecasting models (Informer, DLinear, TimesNet, iTransformer) and their respective variants enhanced with the proposed GLAFF framework. Lower values indicate better performance. The table shows results for different prediction horizons (96, 192, 336, 720) across multiple datasets.
read the caption
Table 1: The forecasting errors for multivariate time series among GLAFF and mainstream baselines. A lower outcome indicates a better prediction. The best results are highlighted in bold.
Full paper#