↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Dimensionality reduction (DR) is vital for data analysis, with neighborhood embedding (NE) methods forming the foundation of many modern techniques. However, existing NE algorithms struggle with large datasets and incremental updates. Parametric methods, which utilize neural networks, address these scalability issues but often compromise local structure preservation, a key weakness highlighted in the paper. This is attributed to insufficient repulsive forces on negative data pairs and an unsuitable loss function.
To tackle these challenges, the researchers introduce ParamRepulsor. This novel parametric method incorporates hard negative mining, identifying and emphasizing challenging negative pairs, and uses a loss function optimized for the parametric context. This results in significantly improved local structure preservation, without sacrificing the fidelity of global structure representation. ParamRepulsor outperforms existing parametric methods, and even approaches the performance of top non-parametric methods, demonstrating considerable advancements in the field.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in dimensionality reduction and related fields. It highlights a critical performance discrepancy between parametric and non-parametric methods, demonstrating that parametrization can hinder local structure preservation. The proposed method, ParamRepulsor, offers a novel solution to this limitation, paving the way for more adaptable and effective dimensionality reduction techniques, particularly for large, dynamically updated datasets.
Visual Insights#

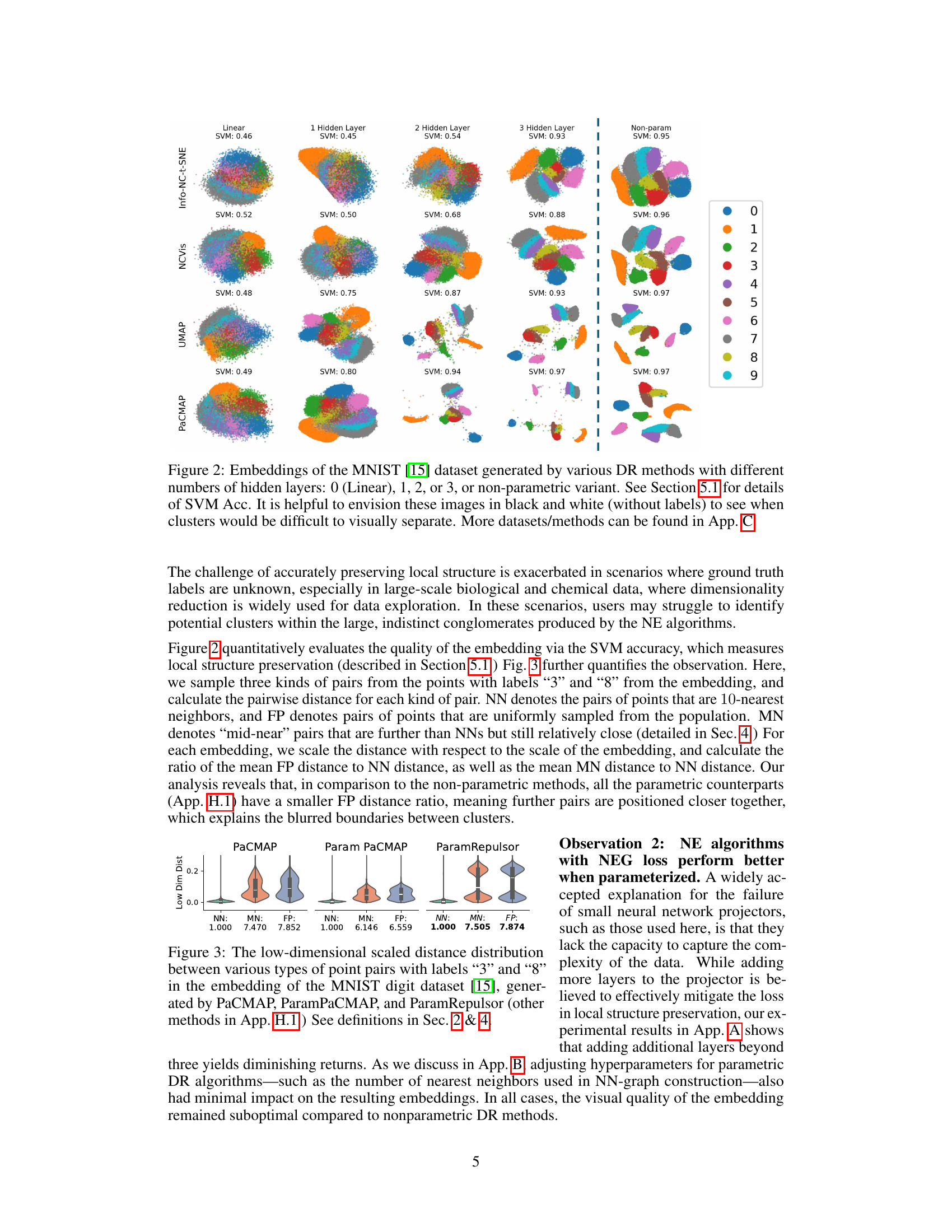
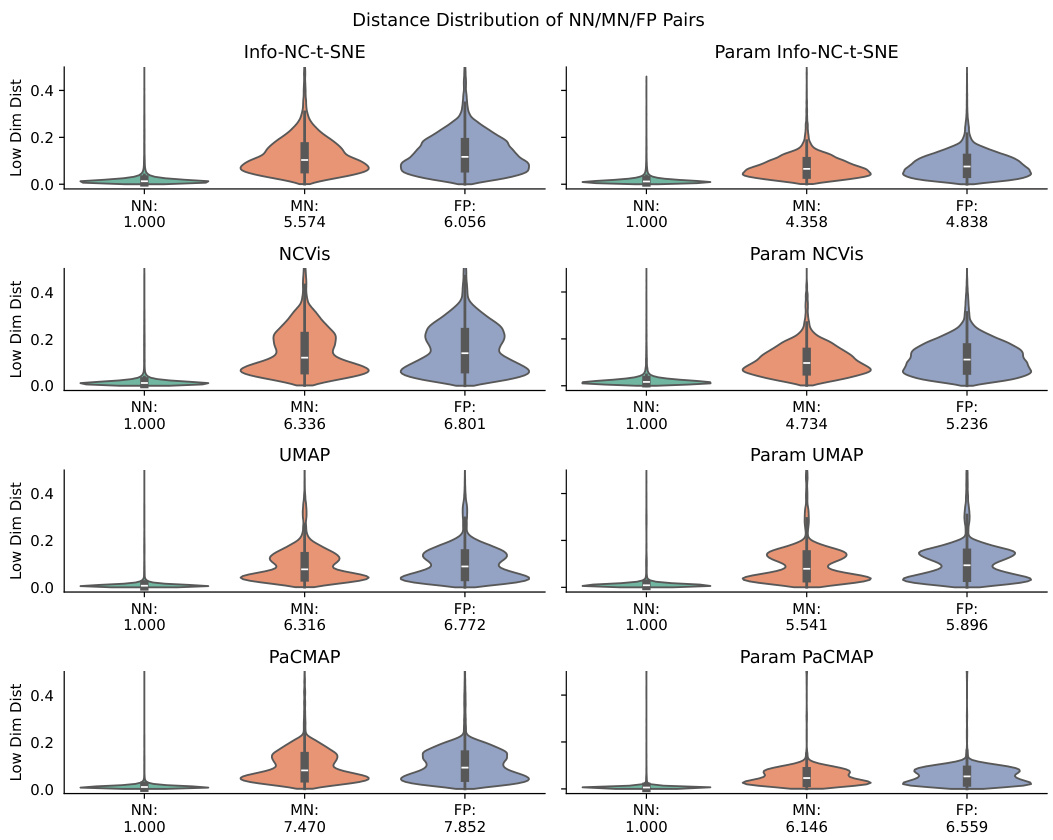
This figure compares the dimensionality reduction results of several parametric and non-parametric methods on the MNIST dataset. The top row shows the results of non-parametric methods (Info-NC-t-SNE, NCVis, UMAP, PaCMAP), while the bottom row shows the results of their parametric counterparts. The figure demonstrates that parametric methods struggle to preserve the local structure of the dataset compared to their non-parametric counterparts. The authors’ proposed method, ParamRepulsor, is shown in the bottom-right corner and achieves superior local structure preservation.
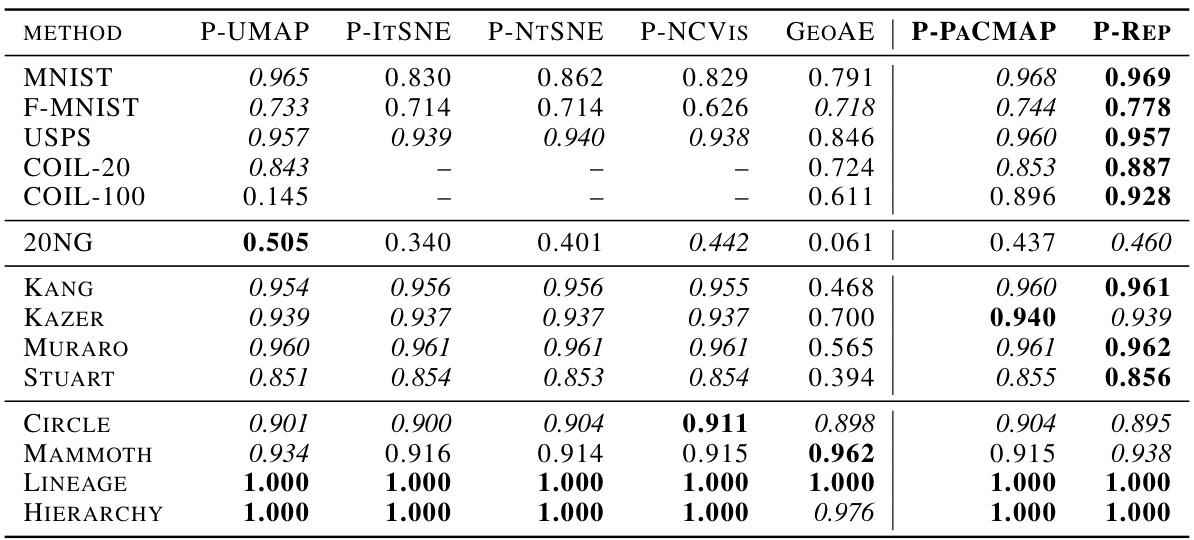
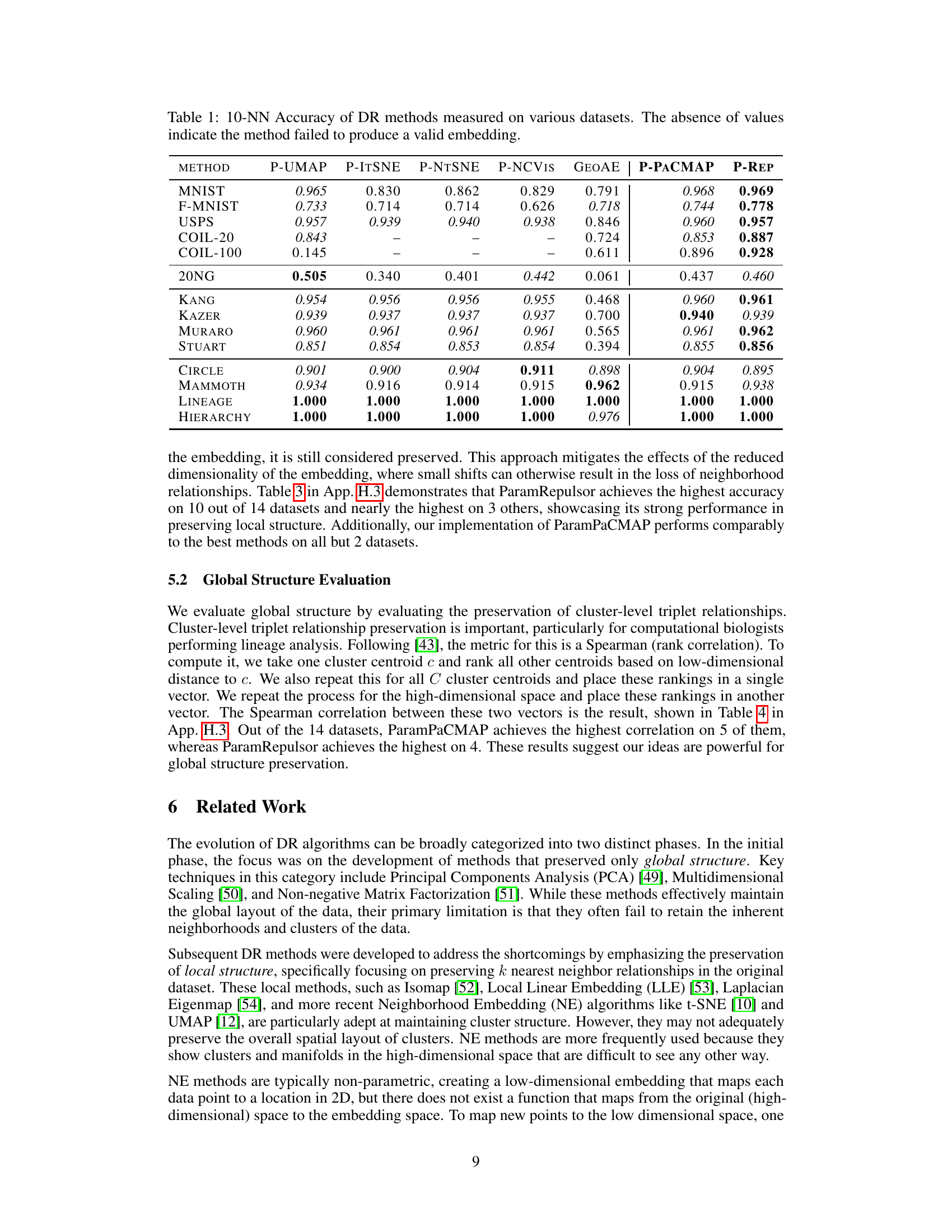
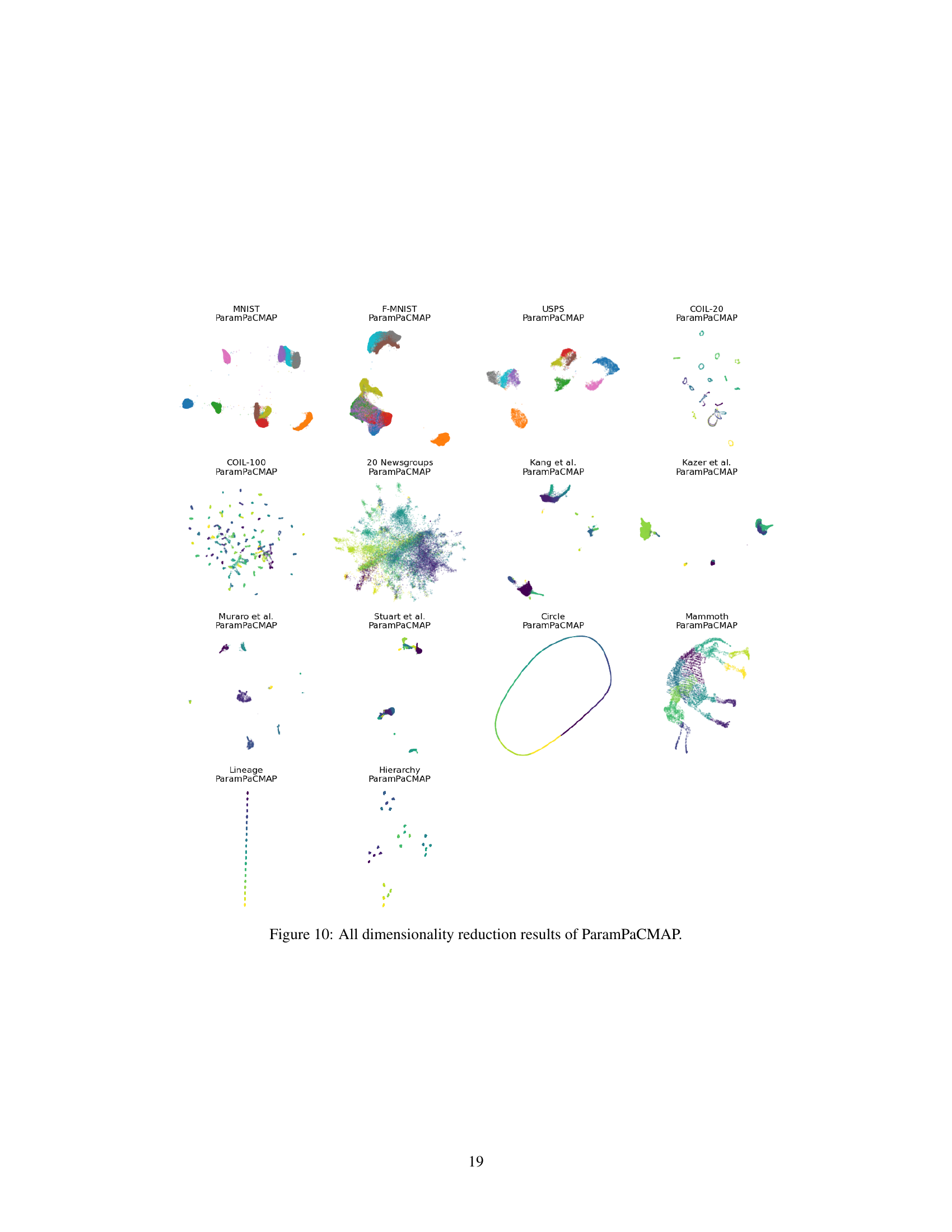
This table presents the 10-Nearest Neighbor (10-NN) accuracy for different dimensionality reduction (DR) methods across a variety of datasets. The 10-NN accuracy is a measure of how well the DR methods preserve the local structure of the data. A higher 10-NN accuracy indicates better preservation of local structure. The absence of values for certain methods and datasets suggests that those methods failed to produce a valid low-dimensional embedding for those datasets.
In-depth insights#
Param. DR Effects#
The section on ‘Param. DR Effects’ would likely explore how the parametrization of dimensionality reduction (DR) algorithms impacts their performance, especially concerning the trade-off between preserving global and local data structures. Parametric methods, using neural networks, offer generalization to unseen data, a significant advantage over non-parametric techniques. However, the analysis would likely reveal that parametrization can compromise the preservation of fine-grained local structures, despite maintaining global fidelity. This is a crucial finding, potentially explaining why, despite their popularity, parametric methods sometimes underperform their non-parametric counterparts in certain visualization tasks. A key aspect of this analysis may be determining whether parametrization’s negative effects on local structure are more pronounced with specific loss functions or neural network architectures. The study would likely offer specific insights into these details, leading to a more nuanced understanding of the strengths and limitations of parametric DR methods and guiding the development of improved techniques.
Hard Negative Mining#
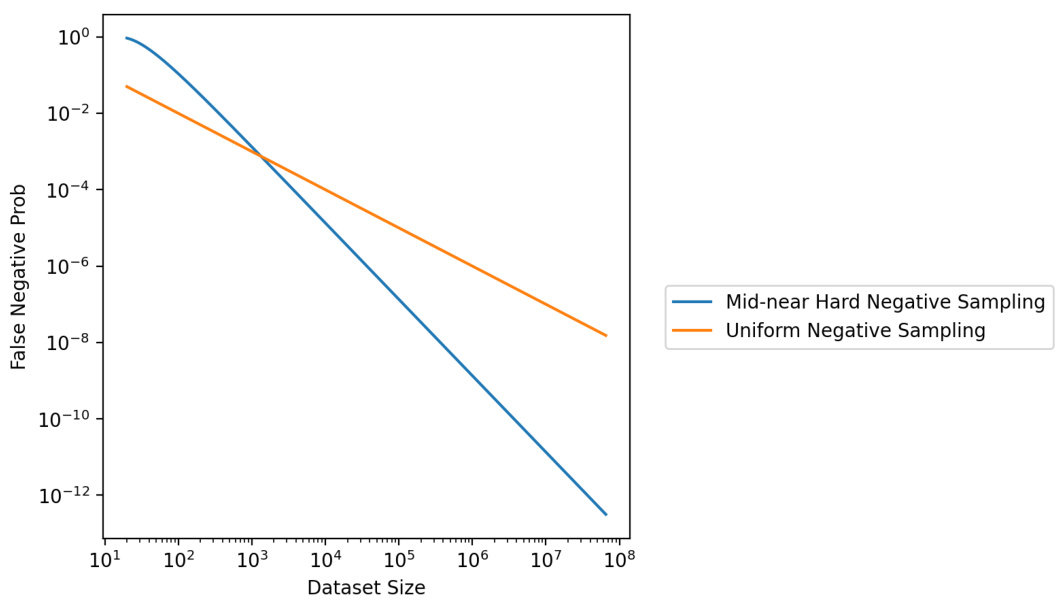
Hard negative mining is a crucial technique in contrastive learning and dimensionality reduction, particularly effective when dealing with parametric methods. It aims to improve the discrimination ability of a model by focusing on those negative samples that are most similar to positive samples. These ‘hard negatives’ pose the greatest challenge for the model, as they lie close to the decision boundary. By explicitly including these hard negatives during training, the model is forced to learn more robust representations and improve its ability to distinguish between similar yet distinct data points. This is particularly important for dimensionality reduction, where the goal is to maintain local structure while mapping high-dimensional data to a lower dimension. The effectiveness of hard negative mining relies on efficient sampling strategies to identify and utilize hard negatives without being computationally prohibitive. The choice of loss function and the interaction with the parametric model are also key factors that influence the final outcome.
Param. Method Limits#
The heading ‘Param. Method Limits’ suggests an exploration of the shortcomings and inherent constraints within parametric dimensionality reduction (DR) methods. The discussion likely centers on how parametrization, while offering generalization benefits, may hinder the preservation of fine-grained local details crucial for accurate data visualization and analysis. A key aspect is the trade-off between preserving global structure (the overall relationships within the data) and local structure (the proximity of individual data points). Parametric methods, due to their reliance on function approximation, might struggle to capture intricate, local patterns. Another limitation might involve the influence of the loss function chosen, which can affect the balance between repulsive and attractive forces between data points. The analysis may also reveal that negative sampling strategies, commonly used in parametric methods, are less effective at repelling negative pairs than non-parametric alternatives. Overall, this section likely provides insights into why despite their strengths, parametric DR methods often require careful consideration and selection to ensure that important local information is not lost during the dimensionality reduction process.
Local Structure Focus#
The concept of “Local Structure Focus” in dimensionality reduction methods centers on preserving the neighborhood relationships within data. High-dimensional data often obscures the underlying local structure, making it challenging to visualize clusters. Effective dimensionality reduction techniques should maintain local neighborhood information in the reduced dimensional space. This is crucial for accurate visualization and data analysis, enabling easier identification of clusters and revealing intricate relationships between data points. Failure to preserve local structure can lead to misleading visualizations and inaccurate interpretations. The methods discussed in this section utilize techniques like k-NN accuracy and SVM accuracy to quantitatively evaluate the preservation of local structure, providing a rigorous assessment of the methods’ ability to capture local neighborhood information effectively. The choice of loss function (e.g. NEG vs. InfoNCE) also significantly impacts the preservation of local structure in parameterized methods. Hard Negative Mining emerges as a crucial technique to improve local structure preservation by focusing on separating difficult-to-distinguish data points, enhancing the clarity and accuracy of the final representation.
Future Research#
Future research directions stemming from this work could involve exploring alternative loss functions beyond NEG to further enhance local structure preservation in parametric dimensionality reduction. Investigating different neural network architectures, such as convolutional networks, could improve the model’s ability to capture complex data relationships. Addressing the computational cost of the proposed method, particularly for large datasets, is crucial for broader applicability. A comprehensive evaluation of different negative sampling strategies beyond hard negative mining, including exploring methods that adaptively select negative samples based on the model’s current performance, warrants further investigation. Finally, developing a theoretical framework to better understand the relationship between parametric and non-parametric methods is needed to guide future algorithmic innovations in dimensionality reduction.
More visual insights#
More on figures
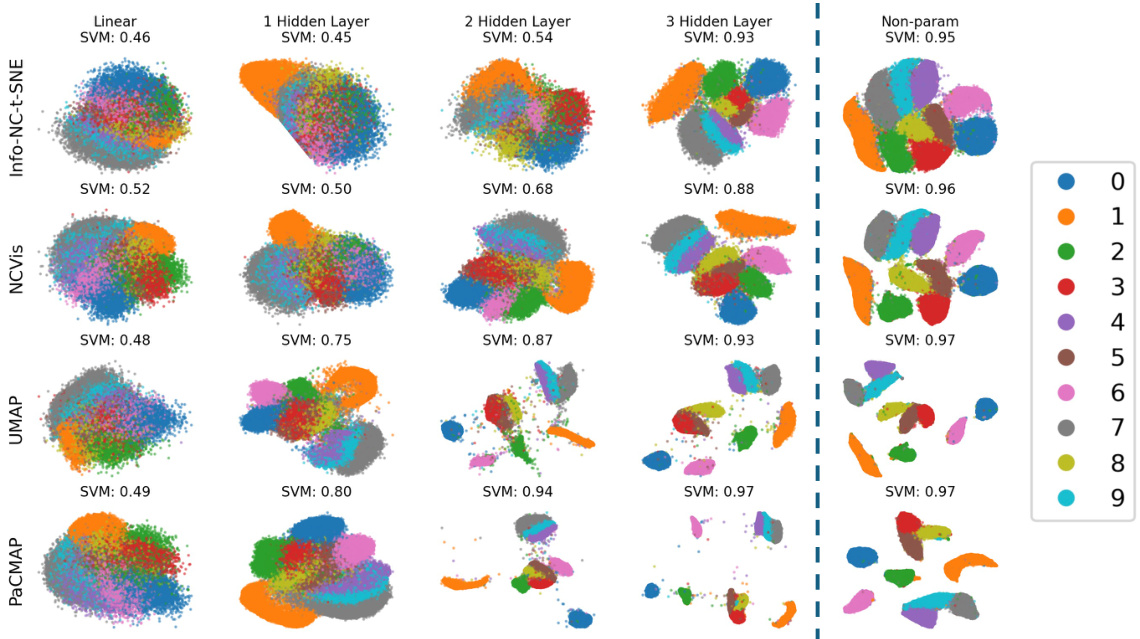
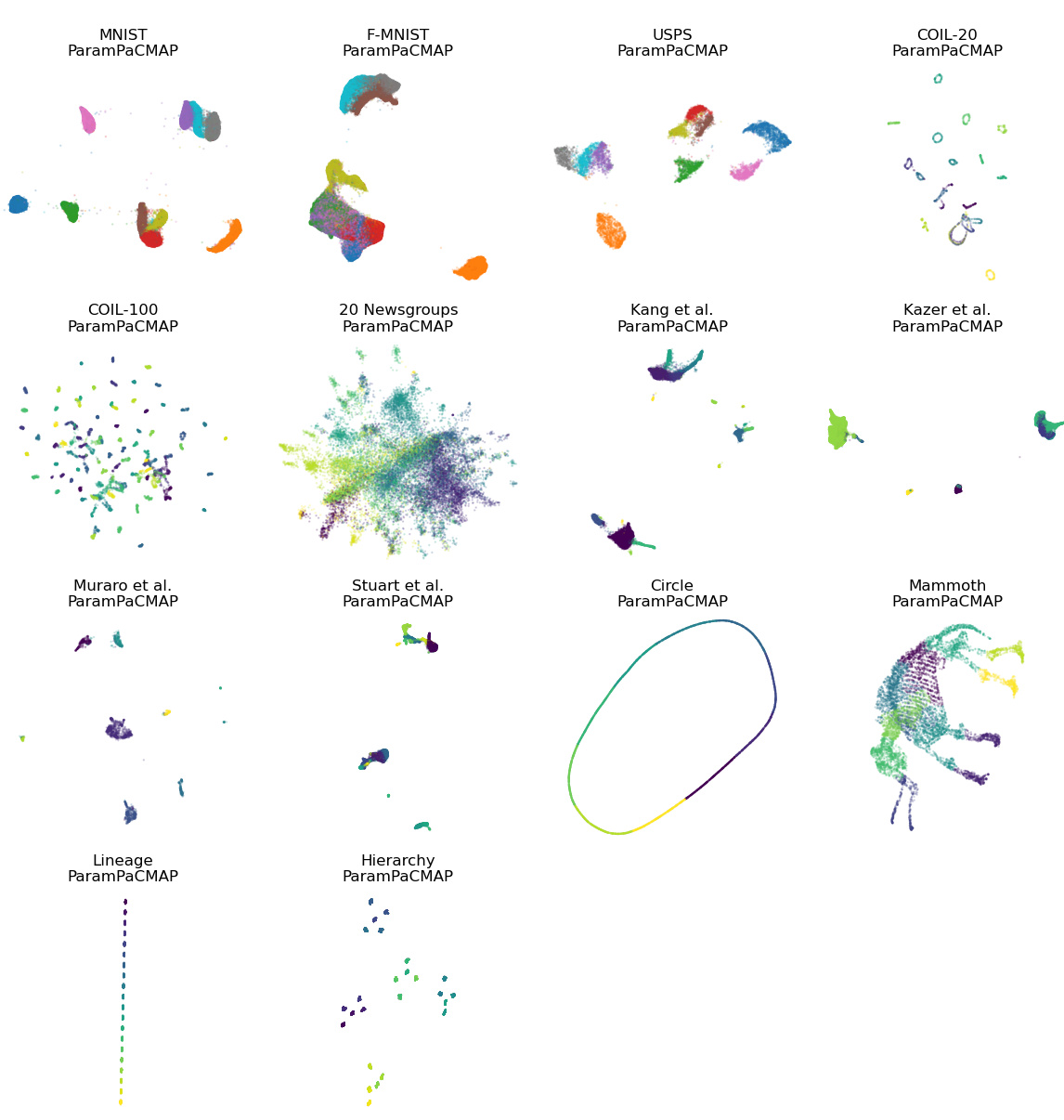
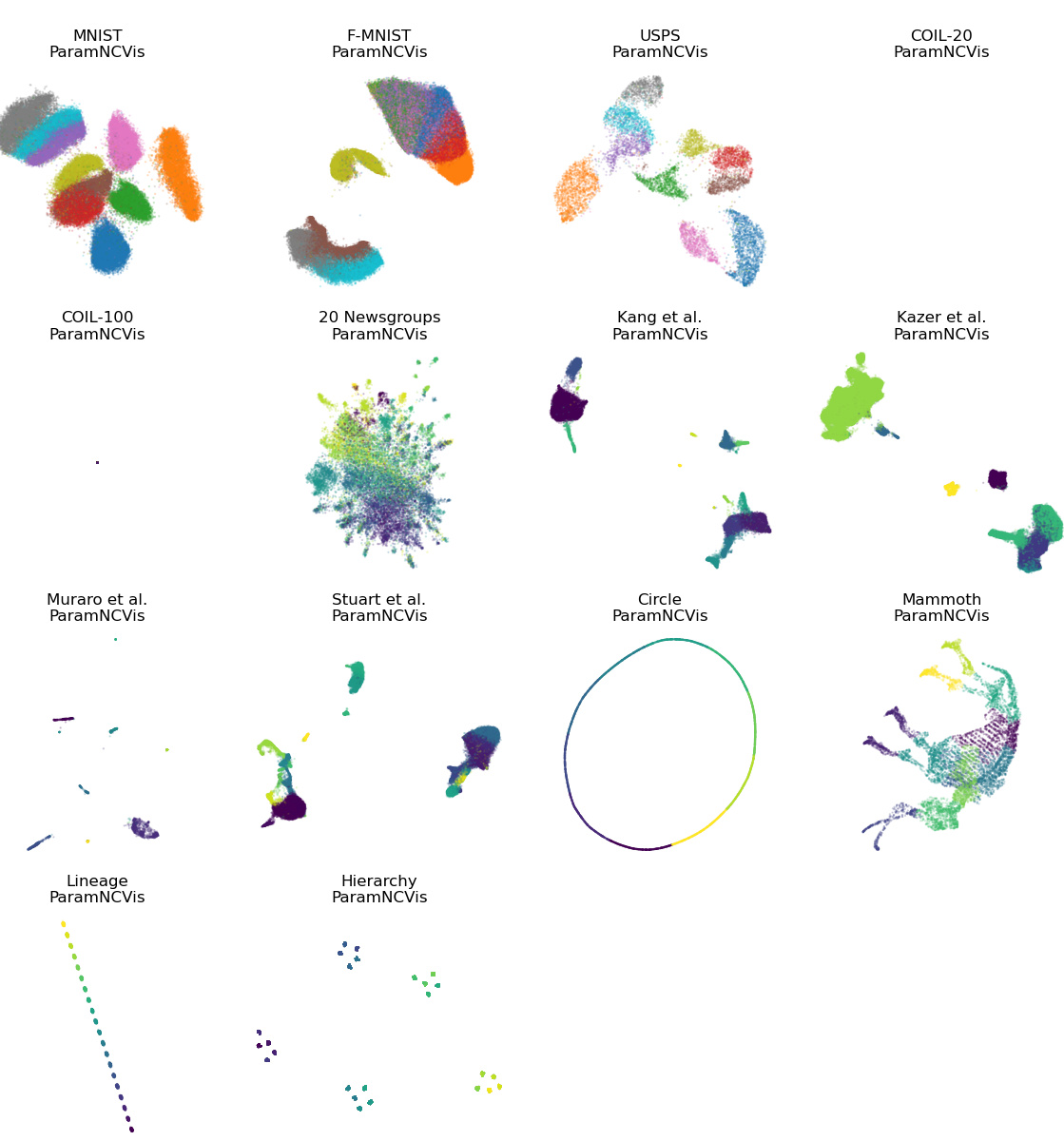
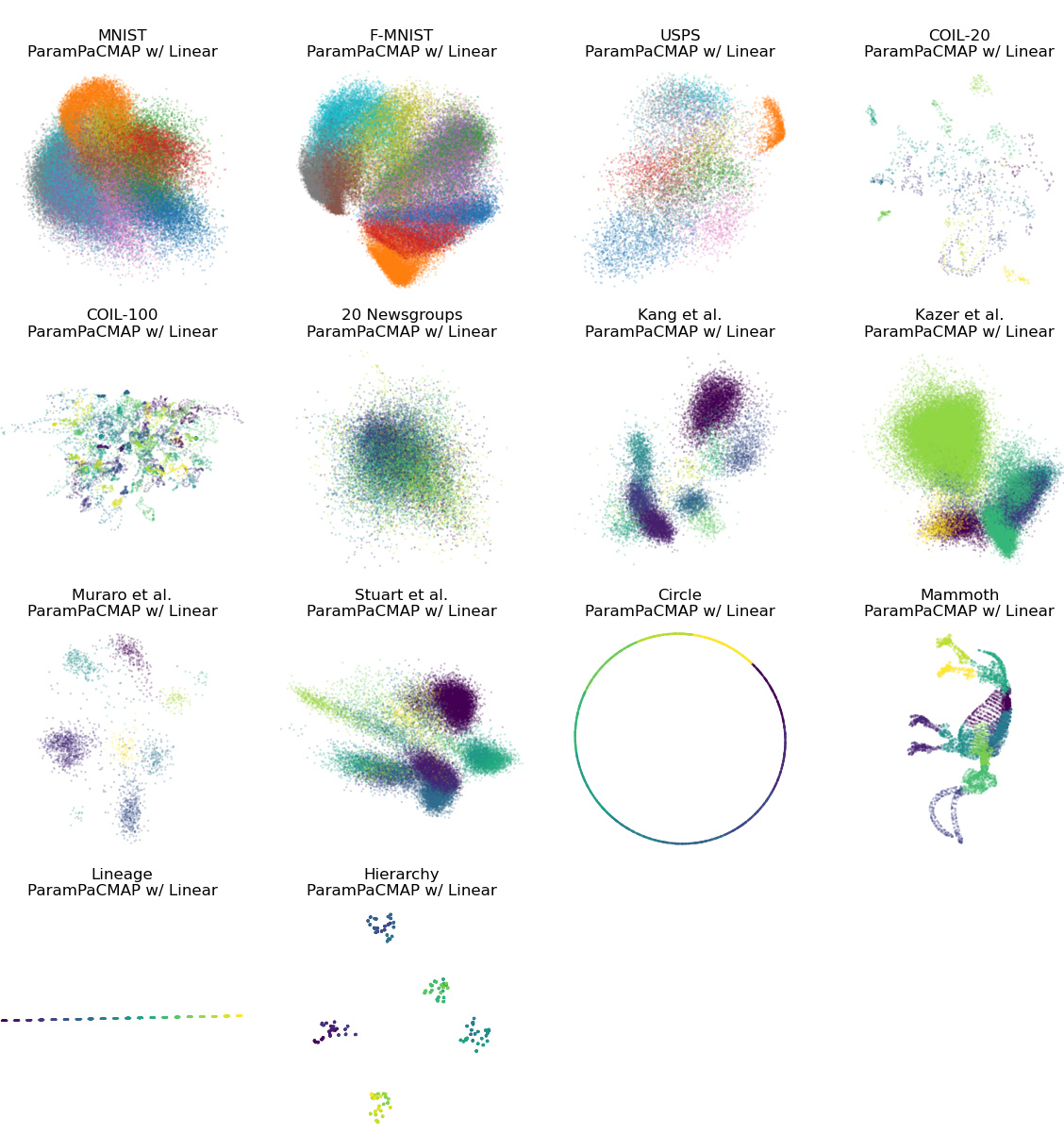
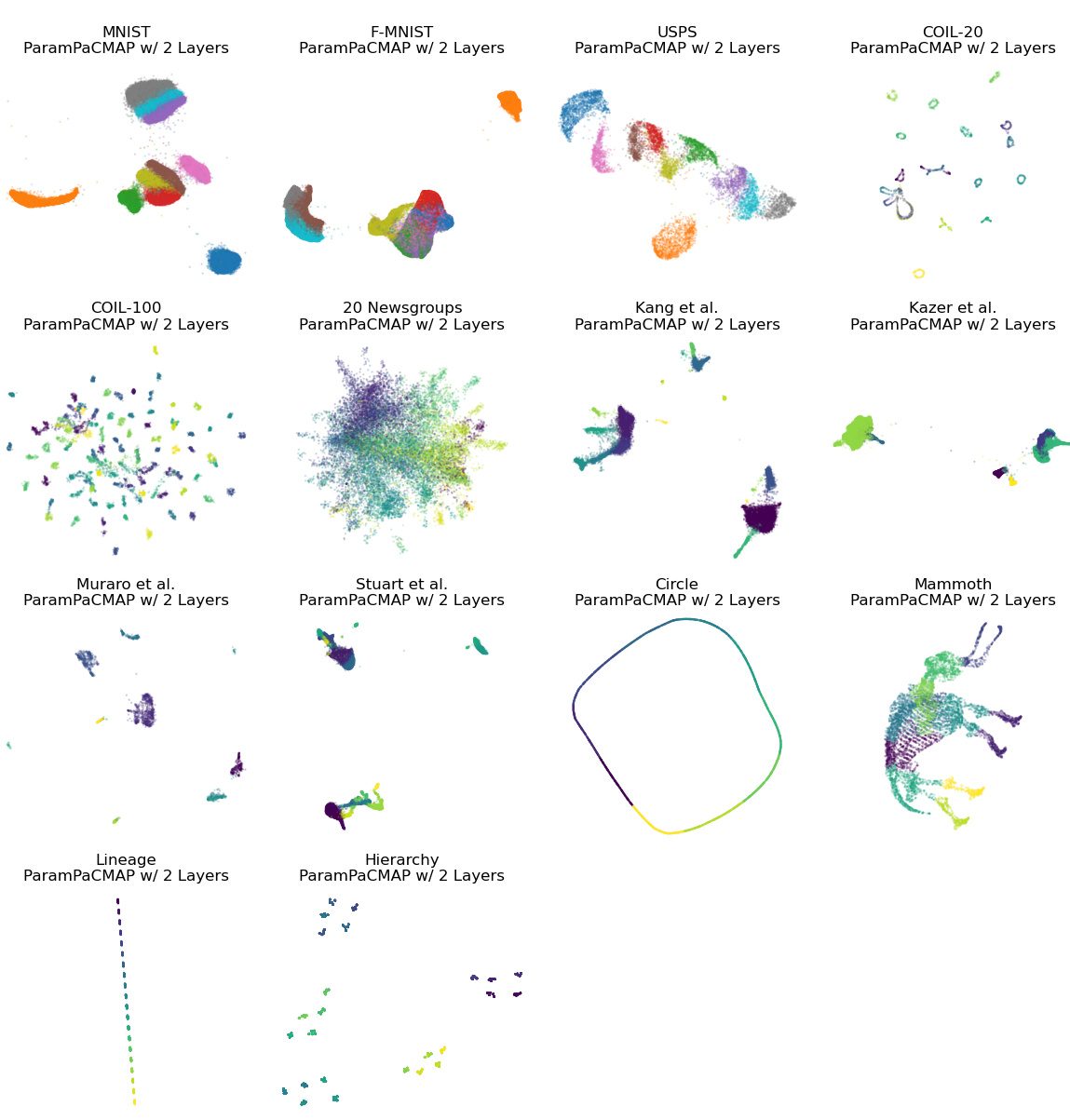
This figure shows the results of dimensionality reduction on the MNIST dataset using various methods. It compares parametric methods (with varying numbers of hidden layers in a neural network) against a non-parametric method. The SVM accuracy (a measure of local structure preservation) is provided for each embedding. The visualization highlights how parametric methods struggle to preserve the distinct separation of clusters compared to the non-parametric approach, particularly with fewer hidden layers.

This figure compares the performance of various dimensionality reduction methods on the MNIST dataset. The top row shows the results of non-parametric methods, while the bottom row shows the results of parametric methods. The figure demonstrates that parametric methods fail to preserve the local structure of the dataset as well as non-parametric methods. The authors’ proposed method, ParamRepulsor, addresses this issue and achieves state-of-the-art performance in local structure preservation.

This figure shows the impact of applying Hard Negative Mining (HNM) to the ParamRepulsor algorithm. The MNIST dataset is used. Different plots show the resulting embeddings with varying coefficients applied to the repulsive force of mid-near pairs, which are considered hard negatives. The circles highlight how clusters are separated better when the coefficient increases, indicating improved local structure preservation while still maintaining the general global structure.

This figure shows an experiment on the MNIST dataset to test the effect of increasing the number of hidden layers in the neural network projector for three different dimensionality reduction methods (Info-NC-t-SNE, UMAP, and PaCMAP). The results indicate that increasing the number of layers beyond three provides minimal improvement in local structure preservation, while the global structure remains largely unaffected.
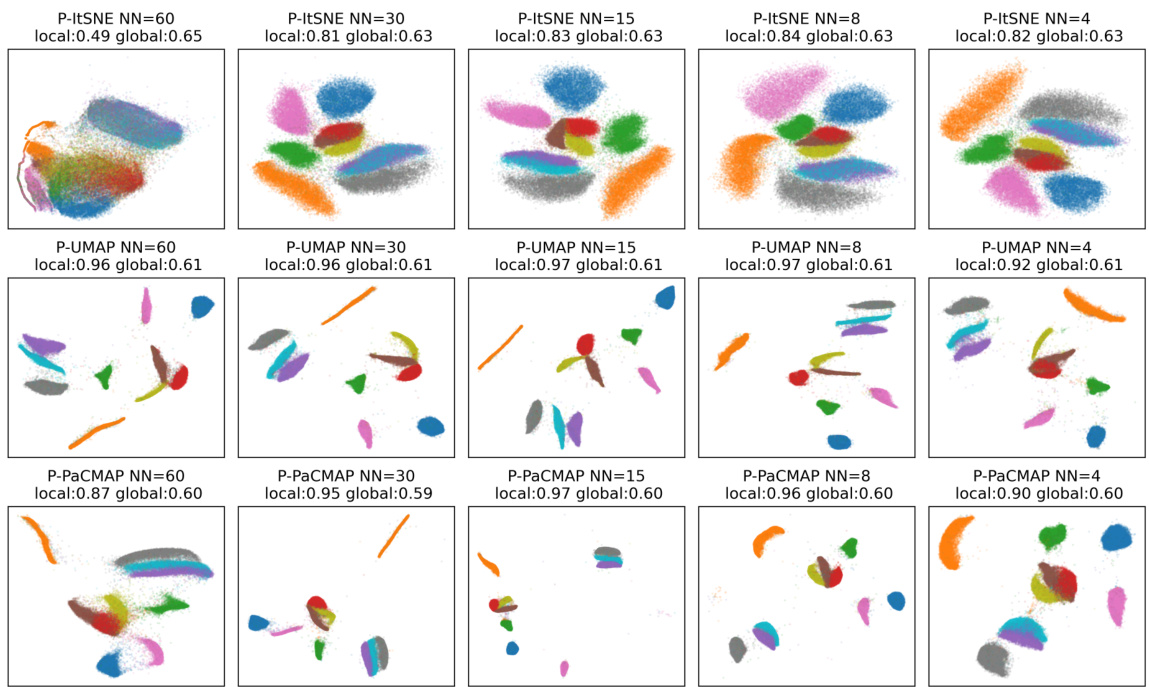
This figure compares the performance of different dimensionality reduction (DR) methods on the MNIST dataset. The top row shows the results of several non-parametric methods, while the bottom row shows the results of their parametric counterparts. The results show that the parametric methods fail to preserve the local structure of the data, meaning they struggle to accurately represent the relationships between nearby data points. In contrast, the authors’ new method, ParamRepulsor, is shown to significantly improve the preservation of local structure in parametric DR methods, suggesting that their improvements address a significant weakness in existing methods. Hard Negative Mining is highlighted as a key component of their improved approach.

This figure compares the performance of various dimensionality reduction methods on the MNIST dataset. The top row shows the results of non-parametric methods, which preserve local structure well. The bottom row displays the results of parametric methods, which fail to preserve the local structure, showing blurred cluster boundaries. The authors’ proposed method, ParamRepulsor, is shown to significantly improve local structure preservation compared to other parametric approaches, effectively resolving this shortcoming through a technique called Hard Negative Mining.

This figure compares the performance of several dimensionality reduction (DR) methods on the MNIST dataset. The top row shows the results of non-parametric methods, while the bottom row shows the results of parametric methods. The figure demonstrates that parametric methods fail to preserve the local structure of the dataset as well as non-parametric methods. The authors introduce a new parametric method called ParamRepulsor that addresses this issue by incorporating Hard Negative Mining.

This figure compares the performance of parametric and non-parametric dimensionality reduction methods on the MNIST dataset. The top row shows the results of several non-parametric methods, while the bottom row shows the results of their parametric counterparts. It demonstrates that parametric methods struggle to preserve the local structure of the data compared to non-parametric methods. The authors’ proposed method, ParamRepulsor, significantly improves the local structure preservation in parametric methods.
This figure compares the performance of parametric and non-parametric dimensionality reduction methods on the MNIST dataset. The top row shows the results of several well-known non-parametric methods (Info-NC-t-SNE, NCVis, UMAP, PaCMAP), while the bottom row shows the results of their parametric counterparts. The visualization clearly demonstrates that the parametric methods fail to preserve the local structure of the data (the distinct clusters of handwritten digits are blurred together), whereas the non-parametric methods maintain better local structure preservation. The authors’ proposed method, ParamRepulsor, is shown in the bottom-right, successfully addressing the local structure preservation issue present in other parametric methods.
This figure compares the performance of various dimensionality reduction methods on the MNIST dataset. The top row shows non-parametric methods, while the bottom row shows parametric methods. The results demonstrate that parametric methods fail to preserve the local structure of the data as well as the non-parametric methods. ParamRepulsor, a new method developed by the authors, is shown to significantly improve local structure preservation in parametric dimensionality reduction methods.

This figure compares the performance of several dimensionality reduction methods on the MNIST dataset. The top row shows the results of non-parametric methods (t-SNE, NCVis, UMAP, PaCMAP), while the bottom row shows the results of their parametric counterparts. The results demonstrate that parametric methods struggle to preserve the local structure of the data, while the proposed method (ParamRepulsor) improves this significantly by incorporating Hard Negative Mining.
This figure compares the performance of various dimensionality reduction methods on the MNIST dataset. The top row shows results from non-parametric methods (t-SNE, NCVis, UMAP, PaCMAP), demonstrating good preservation of local data structure. The bottom row shows results from parametric versions of the same algorithms, revealing a significant loss of local structure. The last column displays the results of the authors’ proposed method, ParamRepulsor, which shows improved local structure preservation compared to other parametric approaches.

This figure compares the dimensionality reduction results of several parametric and non-parametric methods on the MNIST dataset. It shows that non-parametric methods (top row) preserve local data structure better than parametric methods (bottom row). The authors’ proposed method, ParamRepulsor, significantly improves the local structure preservation of the parametric approach.
This figure compares dimensionality reduction results on the MNIST dataset using various parametric and non-parametric methods. The top row shows the results of non-parametric methods, which effectively preserve local structure, while the bottom row shows the results of parametric methods, which fail to preserve local structure. The authors’ proposed method, ParamRepulsor, is shown in the bottom right and addresses the shortcomings of other parametric methods by preserving both global and local structure.
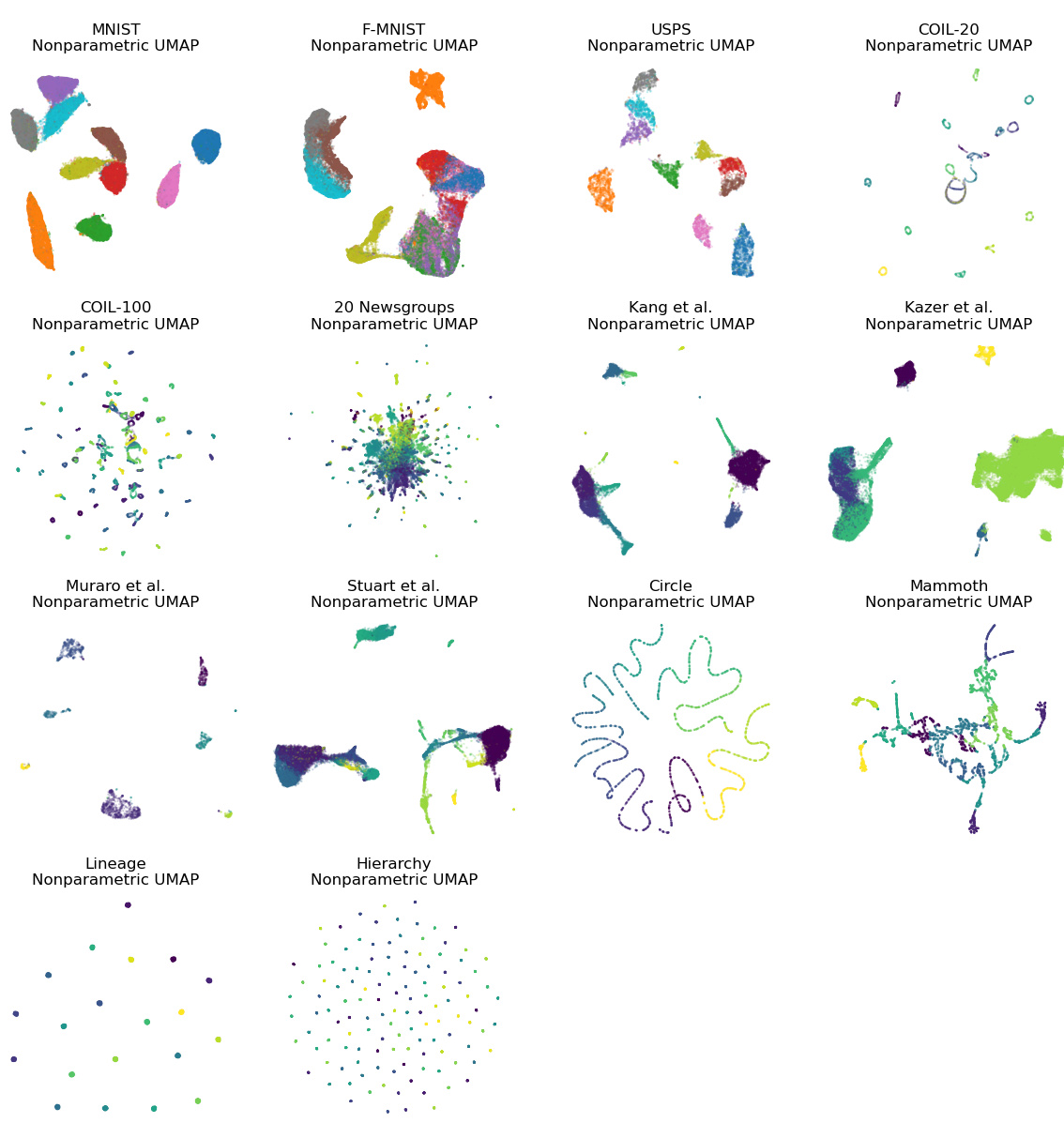
This figure compares the performance of various dimensionality reduction methods on the MNIST dataset. The top row shows the results of non-parametric methods, while the bottom row shows the results of parametric methods. The figure demonstrates that parametric methods struggle to preserve the local structure of the data, while non-parametric methods are much better at preserving this structure. The authors’ new method, ParamRepulsor, is shown to significantly improve the performance of parametric methods in preserving local structure.

This figure compares the performance of different dimensionality reduction methods on the MNIST dataset. The top row shows the results of several non-parametric methods, demonstrating good preservation of local data structure (clusters). The bottom row shows the results of their parametric counterparts, revealing a significant loss of local structure, resulting in blurry clusters. The final column showcases the results of the authors’ proposed method, ParamRepulsor, which successfully recovers the local structure while maintaining global structure, outperforming other parametric methods. Hard Negative Mining is highlighted as the key improvement.
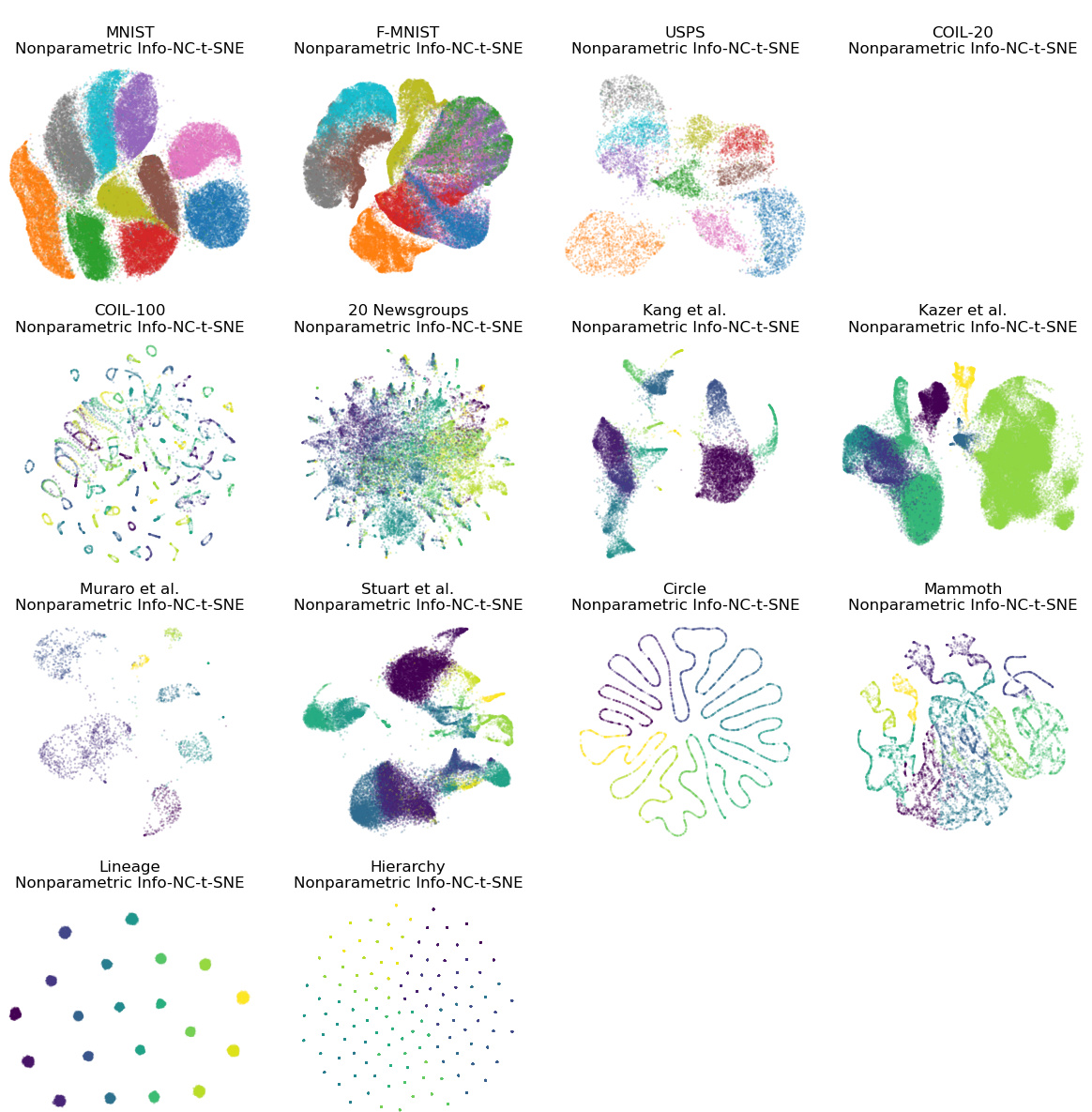
This figure compares the performance of parametric and non-parametric dimensionality reduction methods on the MNIST dataset. The top row shows the results of several established non-parametric methods, while the bottom row displays the results of their parametric counterparts. The visualization clearly demonstrates that parametric methods struggle to preserve the local structure of the data compared to their non-parametric equivalents. The authors’ proposed method, ParamRepulsor, is shown to significantly improve local structure preservation within the parametric methods.

This figure compares the performance of various dimensionality reduction methods on the MNIST dataset. The top row shows the results of non-parametric methods (t-SNE, NCVis, UMAP, PaCMAP), which preserve local structure well. The bottom row shows the results of their parametric counterparts, which fail to preserve local structure. ParamRepulsor, a new method introduced in the paper, is shown to address the shortcomings of parametric methods and achieve results closer to the non-parametric methods.
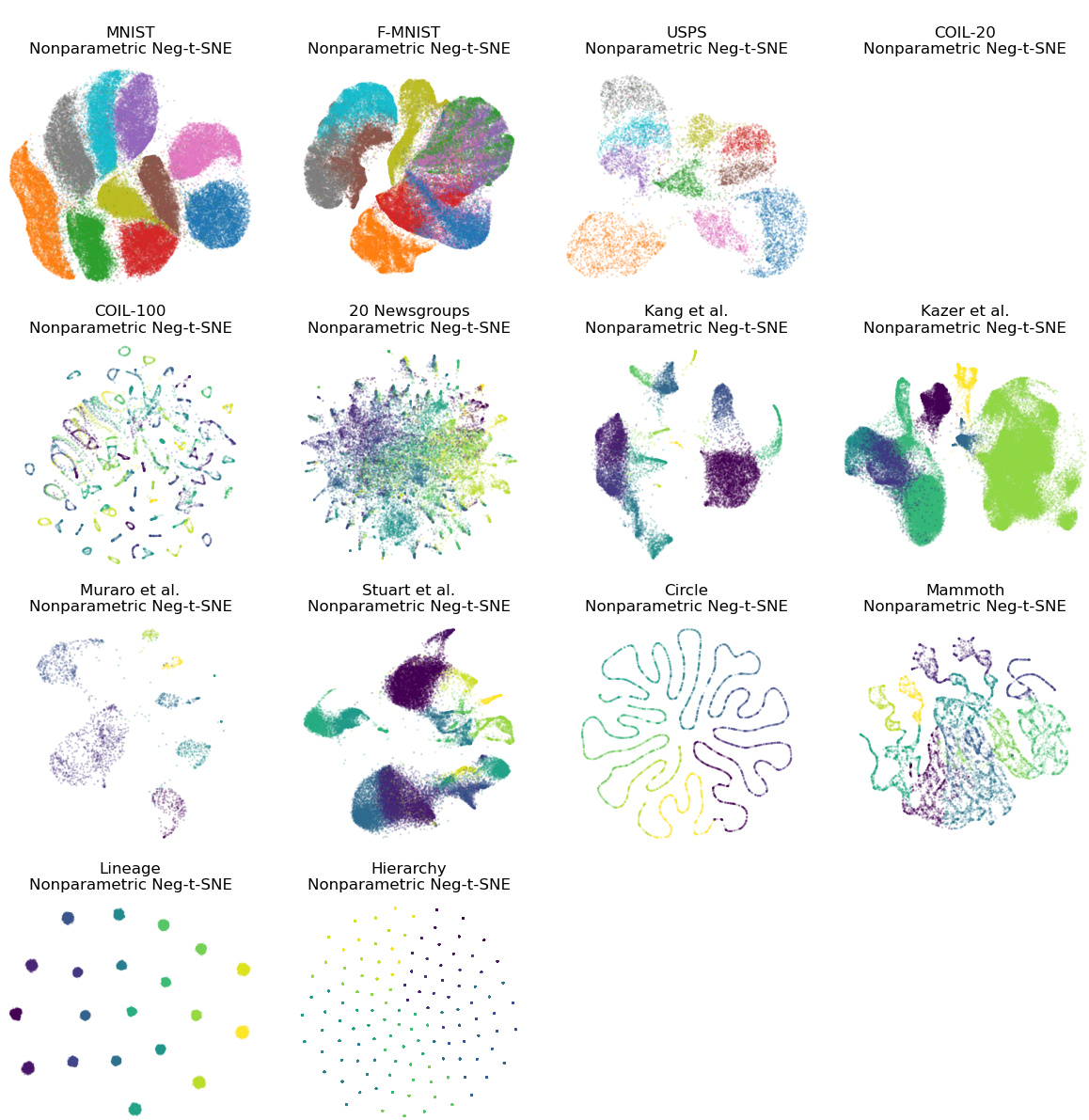
This figure compares the performance of various dimensionality reduction (DR) methods on the MNIST dataset. The top row shows the results of non-parametric methods (t-SNE, NCVis, UMAP, PaCMAP), demonstrating good preservation of local data structure. The bottom row shows the results of their parametric counterparts, which fail to maintain local structure as effectively. The figure highlights that the authors’ new method, ParamRepulsor, significantly improves local structure preservation in the parametric setting.
This figure compares the performance of various dimensionality reduction methods on the MNIST dataset. The top row shows the results of non-parametric methods, while the bottom row shows the results of parametric methods. The figure demonstrates that parametric methods, which are generally preferred for their ability to generalize to unseen data, fail to preserve the local structure of the data as well as non-parametric methods. The authors’ proposed method, ParamRepulsor, is shown to significantly improve upon the performance of existing parametric methods.
This figure compares the performance of various dimensionality reduction (DR) methods on the MNIST dataset. The top row shows the results of non-parametric methods (t-SNE, NCVis, UMAP, PaCMAP), which are known to preserve local structure well. The bottom row shows the results of parametric versions of the same methods. The parametric methods fail to maintain the clear separation and local structure present in the non-parametric versions, demonstrating a key weakness of parametric approaches. The final column showcases the results of ParamRepulsor, the authors’ proposed method. ParamRepulsor successfully recovers the local structure, achieving results comparable to the non-parametric techniques.

This figure compares the performance of various dimensionality reduction methods on the MNIST dataset. The top row shows non-parametric methods, which preserve local structure well. The bottom row shows parametric methods, which fail to preserve local structure as effectively. The authors’ proposed method, ParamRepulsor, is shown in the bottom right and significantly improves local structure preservation compared to other parametric methods.
More on tables

This table presents the 10-Nearest Neighbor accuracy for various dimensionality reduction (DR) methods across multiple datasets. The 10-NN accuracy is a measure of a DR algorithm’s ability to preserve local structure in the data. Higher accuracy indicates better preservation of local structure. The absence of values indicates that the particular DR method failed to produce a valid low-dimensional embedding for that dataset.
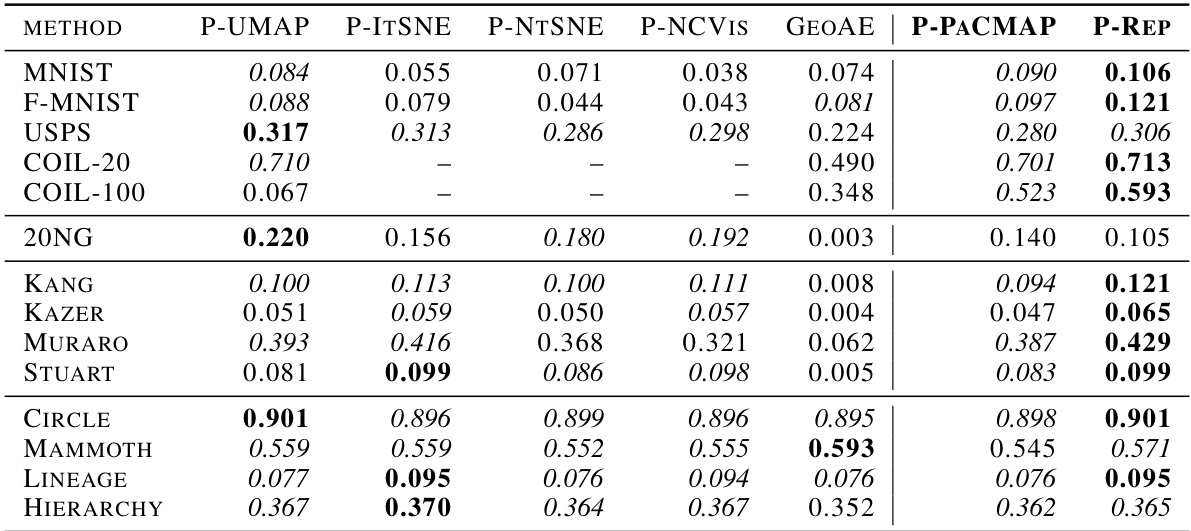
This table presents the ratio of 30-nearest neighbors preserved in the low-dimensional embedding compared to the high-dimensional space for various dimensionality reduction (DR) methods. A higher ratio indicates better preservation of local neighborhood structure. The methods compared include both parametric and non-parametric versions of several algorithms on a variety of datasets, showing the impact of parametrization on local structure preservation.
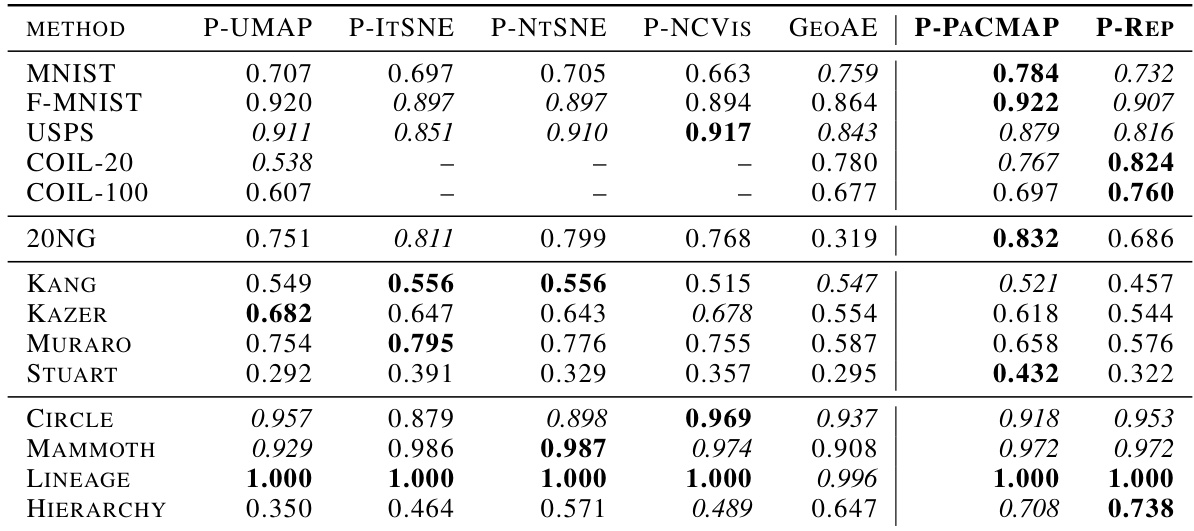
This table presents the 10-Nearest Neighbor accuracy for various dimensionality reduction methods across a range of datasets. The 10-NN accuracy is a measure of how well the methods preserve local structure in the low-dimensional embedding. Higher values indicate better preservation of local structure. The absence of values indicates that the method failed to produce a valid embedding for that particular dataset.

This table presents the SVM accuracy achieved by various dimensionality reduction methods on 14 different datasets. The SVM accuracy serves as a metric for evaluating the methods’ ability to preserve local structure in the low-dimensional embeddings. A higher accuracy indicates better preservation of local structure. The absence of values suggests that the corresponding method failed to generate a valid embedding for that specific dataset.
Full paper#