Graph Neural Networks Need Cluster-Normalize-Activate Modules

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with Graph Neural Networks (GNNs). It introduces a novel, plug-and-play module (CNA) that effectively addresses the oversmoothing issue, significantly improving GNN accuracy and efficiency. This opens exciting new avenues for designing deeper and more expressive GNN architectures, impacting various applications in machine learning on graphs.

Visual Insights

#

This figure visualizes the evolution of node embeddings during the training process of a graph neural network (GNN) on the Cora dataset. It compares the performance of a baseline GNN model to one using the proposed Cluster-Normalize-Activate (CNA) modules. The top row shows the baseline model’s node embeddings at epochs 1, 50, and 100. The bottom row shows the same for the model with CNA modules. Each point represents a node, and the color indicates its class label. The visualization helps to demonstrate how CNA improves the separation of node embeddings belonging to different classes, thus mitigating the problem of oversmoothing.

This table presents the results of graph classification experiments comparing the performance of GNNs with and without CNA modules. It shows that across four different GNN architectures (GCN, GraphSAGE, TransformerConv, and GAT), incorporating CNA consistently leads to a significant increase in accuracy. The improvement is substantial and consistent across all the tested models.

In-depth insights

#

GNN Oversmoothing

#

Graph Neural Networks (GNNs), while powerful for graph-structured data, suffer from oversmoothing. Oversmoothing is a phenomenon where, as the network deepens, node feature representations converge to a single point, hindering the model’s ability to discriminate between nodes and limiting its expressiveness. This convergence is particularly detrimental for complex tasks requiring the capture of high-level relationships between nodes. The paper tackles this challenge by proposing Cluster-Normalize-Activate (CNA) modules. These modules introduce a novel inductive bias to combat oversmoothing, leveraging clustering to maintain feature diversity and enabling the use of substantially deeper networks. CNA’s effectiveness is demonstrated through extensive experiments, showing improved accuracy on node classification and property prediction tasks compared to state-of-the-art baselines while simultaneously using significantly fewer parameters. The methodology suggests a practical approach to address a fundamental limitation of GNNs, paving the way for more complex and powerful GNN architectures.

CNA Module Design

#

The core of the proposed method lies in the innovative design of the Cluster-Normalize-Activate (CNA) module. This module tackles the oversmoothing issue prevalent in deep Graph Neural Networks (GNNs) by introducing a three-step process. First, a clustering mechanism groups nodes with similar feature representations, effectively forming ‘super-nodes’. Second, a normalization step stabilizes training and prevents feature collapse within each cluster. Finally, individual learnable activation functions are applied to each cluster, enhancing the model’s expressiveness and preventing the homogenization of node features. The use of rational activations is particularly noteworthy, offering powerful non-linearity while maintaining computational efficiency. The design cleverly combines unsupervised learning (clustering) with learnable parameters (activation functions) to create an adaptive and flexible module suitable for integration into various existing GNN architectures, improving accuracy and depth without substantial increases in parameters. The strategic combination of these steps provides a principled approach to overcoming limitations of traditional activation functions in GNNs, significantly enhancing their representational capacity and generalization ability.

CNA Effectiveness

#

The effectiveness of Cluster-Normalize-Activate (CNA) modules hinges on their ability to mitigate oversmoothing in deep Graph Neural Networks (GNNs) while enhancing representational power. CNA’s multi-step process, involving clustering nodes with similar features, normalizing within clusters, and applying distinct activation functions to each cluster, is crucial. Empirical results across diverse datasets and GNN architectures demonstrate improved accuracy in node classification, regression, and graph classification tasks. The effectiveness is particularly pronounced in deeper networks, where oversmoothing is a significant problem. Key to CNA’s success is the combination of these steps, as ablation studies reveal that removing any single step diminishes performance. Although the paper doesn’t delve into theoretical guarantees, the experimental evidence strongly suggests that CNA’s impact stems from preventing feature convergence and preserving node distinctiveness throughout training, leading to more expressive and accurate GNN models. Furthermore, CNA demonstrably enhances model compactness, achieving comparable or better performance with fewer parameters compared to state-of-the-art alternatives. This combination of improved accuracy, efficiency, and robustness makes CNA a promising and potentially transformative module for future GNN architectures.

Parameter Efficiency

#

Parameter efficiency is a crucial aspect of machine learning model development, especially for resource-constrained applications or large-scale deployments. The paper investigates this by introducing Cluster-Normalize-Activate (CNA) modules. The core idea is to reduce the number of learnable parameters without sacrificing performance. CNA achieves this by creating clusters of nodes with similar features, normalizing them individually, and then applying distinct activation functions to each cluster. This modular approach allows for learning more expressive representations with fewer parameters compared to existing methods. The empirical evaluation showcases that GNNs with CNA modules consistently outperform baseline GNNs across various datasets and tasks, demonstrating the practical benefits of this approach. This compactness is particularly beneficial when dealing with large graphs, where memory constraints can significantly impact model training and inference.

Future GNN Research

#

Future Graph Neural Network (GNN) research should prioritize addressing the limitations of current models. Overcoming oversmoothing and undersmoothing remains crucial, potentially through more sophisticated activation functions or novel architectural designs that dynamically control information flow. Developing more efficient training methods is essential, especially for very large graphs, which may involve exploring techniques such as graph sparsification or distributed training. Improving expressivity is key, perhaps by incorporating inductive biases based on domain knowledge or developing new types of aggregation and message-passing mechanisms that capture more nuanced relationships within the graph data. Finally, further investigation into theoretical frameworks to better understand the capabilities and limitations of GNNs is needed to guide future development.

More visual insights

#

More on figures

This figure compares the standard activation function (ReLU) with the proposed Cluster-Normalize-Activate (CNA) module. The top row shows a standard GNN, where after each aggregation and update step, the ReLU function is applied to all nodes uniformly. This leads to oversmoothing in deeper networks, where node features converge to a single point. The bottom row illustrates the CNA module. After aggregation and update, nodes are clustered into groups (shown by different colors). Then, each cluster has its features normalized separately. Finally, a distinct learned activation function is applied to each cluster. This process helps to maintain the distinction between node features and prevents oversmoothing, even with deeper networks.

This figure illustrates the three steps of the Cluster-Normalize-Activate (CNA) module. First, the node features are clustered into groups. Then, each cluster’s features are normalized independently. Finally, a separate activation function is applied to each cluster. The figure visually shows the process using different colored nodes representing different clusters and demonstrates how the CNA module transforms the node features layer by layer.

The figure displays the accuracy of various GNN architectures (GAT, GCN, GraphSAGE, and TransformerConv) with and without the CNA module on the Cora and CiteSeer datasets. It shows how the accuracy of standard GNNs decreases significantly with increasing depth due to oversmoothing. In contrast, GNNs with CNA maintain high accuracy even at greater depths, demonstrating CNA’s effectiveness in mitigating oversmoothing.

The figure shows the accuracy of different GNN architectures (GAT, GCN, GraphSAGE) with and without CNA modules on Cora and CiteSeer datasets as the number of layers increases. It demonstrates that CNA helps limit oversmoothing and maintain high accuracy even with deeper networks, outperforming other methods.

This heatmap shows the sensitivity analysis of the hyperparameters: the number of hidden features and the number of clusters per layer on the Cora dataset using GCN. The color in each cell represents the accuracy achieved with the corresponding hyperparameter setting. It illustrates that the model is robust to the choice of hyperparameters and performs best with moderate numbers of features and clusters.

More on tables

This table presents the normalized mean squared error (NMSE) results for different GNN models on two multiscale node regression datasets: Chameleon and Squirrel. It compares the performance of various GNN models (GCN, GAT, PairNorm, GCNII, G2-GCN, G2-GAT, and Trans.Conv) with and without the proposed CNA module. Lower NMSE values indicate better performance. The results show that adding the CNA module consistently improves the performance of the TransformerConv model on both datasets, significantly reducing the NMSE.

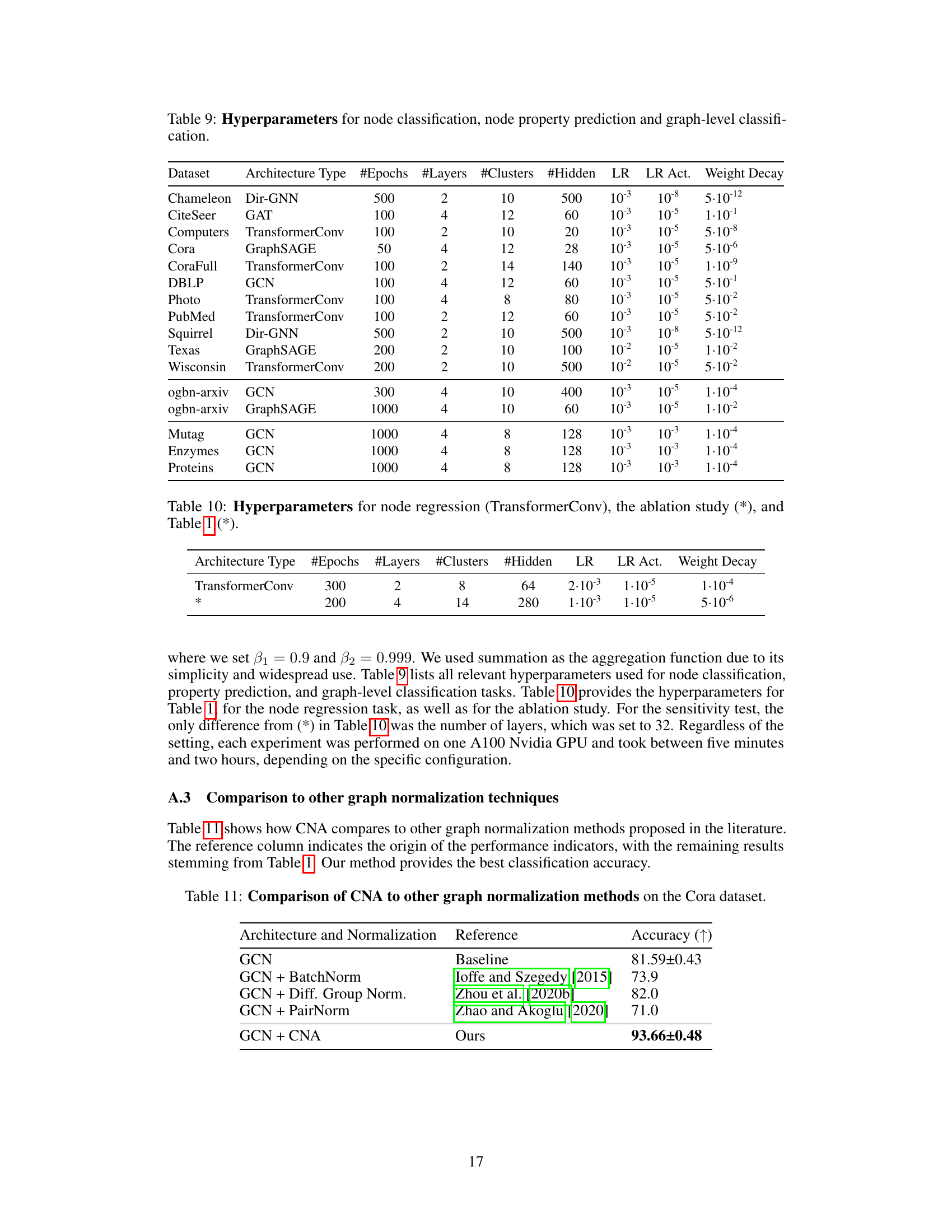
This table compares the performance of the proposed CNA method against state-of-the-art results reported on Papers with Code for eleven node classification datasets. It shows that CNA achieves better accuracy than the best-performing methods on eight out of the eleven datasets, significantly outperforming others on datasets such as Cora and CiteSeer.

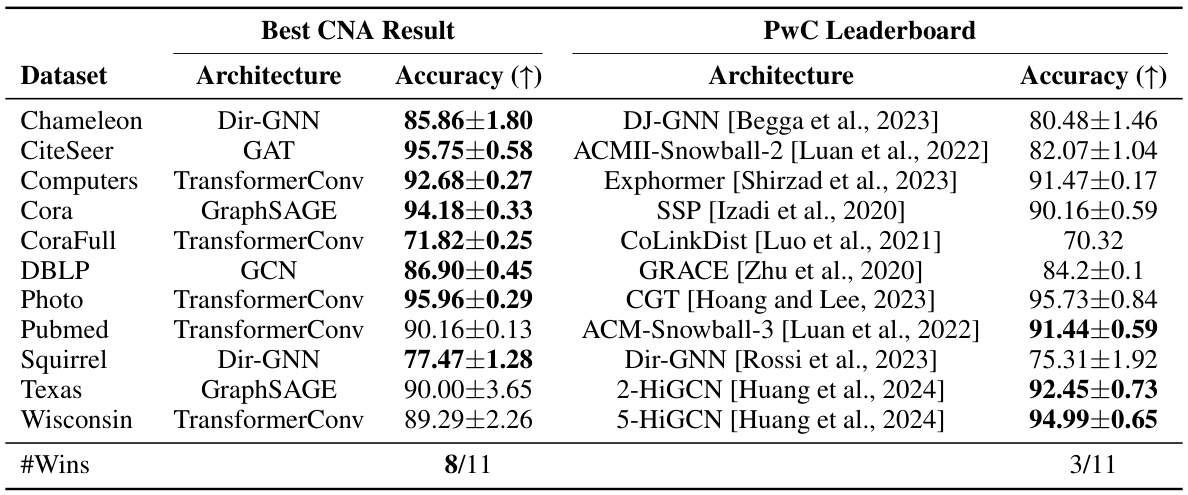
This table and figure compare the performance and the number of parameters of various GNN models, including those enhanced with CNA modules, on the ogbn-arxiv dataset. The results show that CNA enables the creation of smaller models that achieve comparable or better accuracy than larger, more complex models.

This table presents the characteristics of the datasets used in the paper’s experiments to evaluate the CNA module. For each dataset, it lists the number of nodes, edges, features, classes, the node homophily ratio, and whether the classes are balanced. It also notes which datasets were used for node classification, node property prediction, and regression tasks.

This table presents information about the graph-level datasets used to evaluate the Cluster-Normalize-Activate (CNA) modules. For each dataset, the number of graphs, average number of nodes, average number of edges, number of features, number of classes, and whether the classes are balanced are shown. This helps understand the characteristics of the datasets used for evaluating the effectiveness of CNA in graph-level classification tasks.

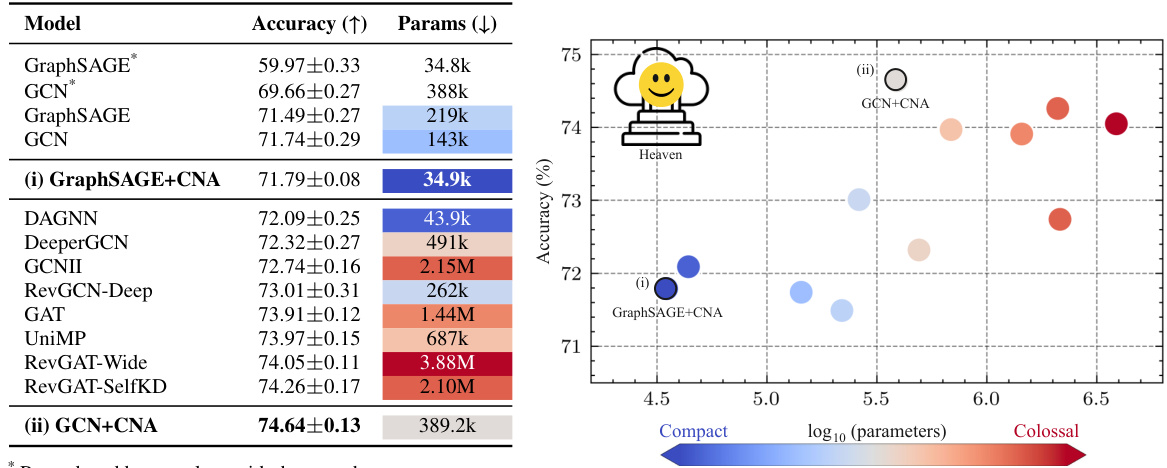
This table lists the hyperparameters used for node classification, node property prediction, and graph-level classification tasks in the paper’s experiments. It includes details such as the architecture type, number of epochs, number of layers, number of clusters, number of hidden units, learning rate, learning rate for activation function, and weight decay for each dataset used in the experiments. These hyperparameters were tuned for optimal performance on each task and dataset.

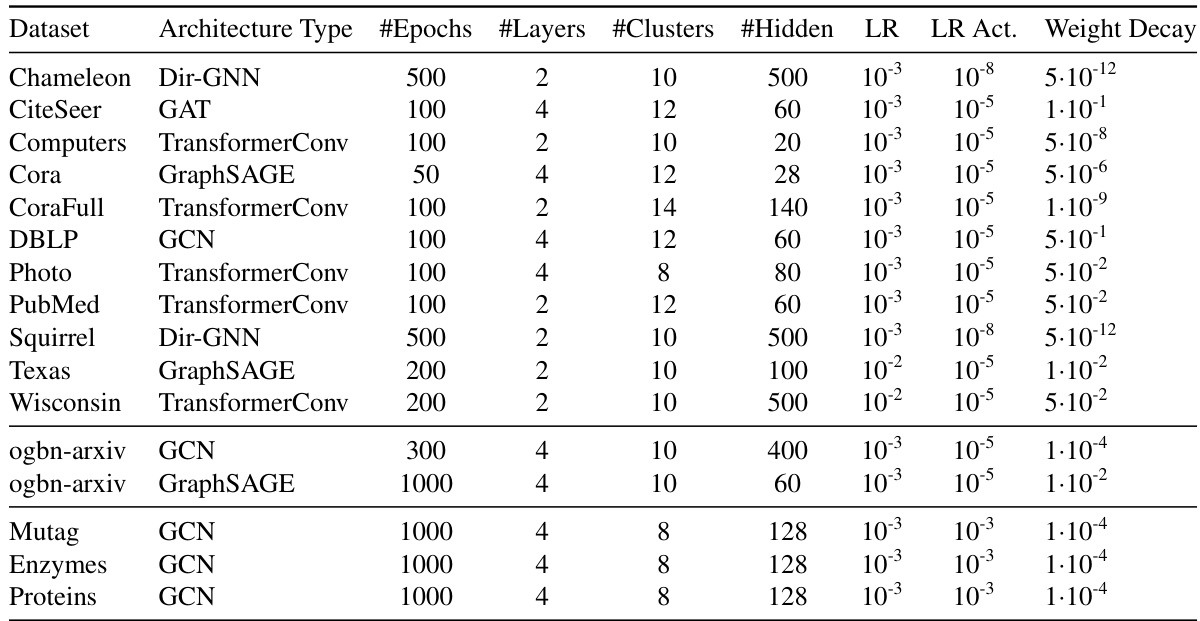
This table presents the hyperparameters used for node regression using the TransformerConv architecture and for the ablation study. The ablation study uses a different number of layers (4) and hidden units (280) compared to the main TransformerConv setup (2 layers and 64 hidden units). The values include the number of epochs, number of layers, number of clusters, number of hidden units, learning rate (LR), activation learning rate (LR Act.), and weight decay. The ‘*’ denotes entries that deviate from the main setup.

This table presents a comparison of different graph neural network (GNN) architectures on the Cora dataset. The ‘Baseline’ column shows the accuracy achieved by each architecture without the proposed Cluster-Normalize-Activate (CNA) module. The ‘CNA’ column shows the improvement in accuracy when the CNA module is added. The results demonstrate that the CNA module consistently improves the accuracy across all architectures tested on the Cora dataset.

Full paper

#