AdjointDEIS: Efficient Gradients for Diffusion Models

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in machine learning and generative models because it introduces AdjointDEIS, a novel and efficient method for training diffusion models. It offers a significant improvement in computational efficiency and memory usage, which directly tackles a major obstacle in training large, complex generative models. The improved efficiency enables researchers to explore more complex architectures and guided image generation tasks with diffusion models which have proven to be state-of-the-art on numerous tasks and will likely continue to for some time.

Visual Insights

#

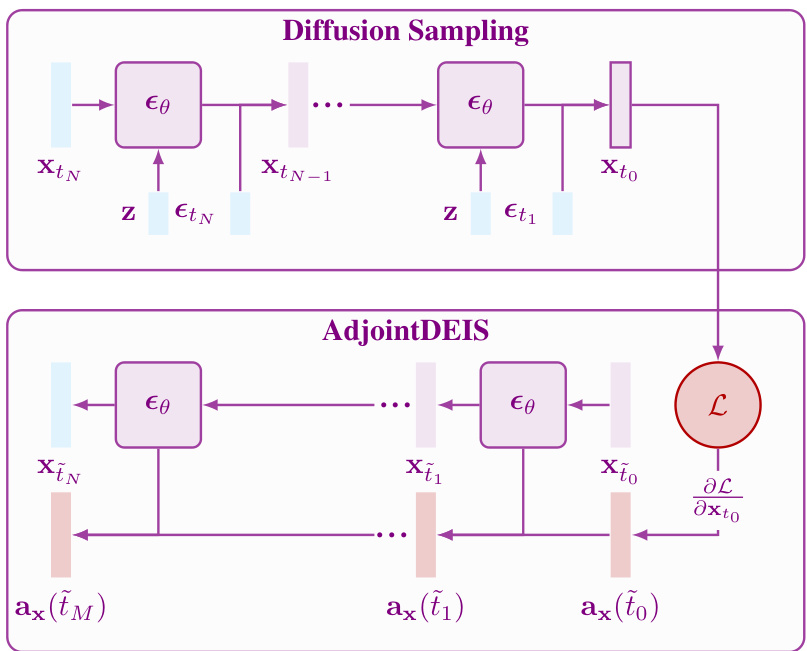
This figure illustrates the AdjointDEIS method for solving the continuous adjoint equations in diffusion models. It shows two parts: diffusion sampling and AdjointDEIS. The diffusion sampling part depicts the forward process of generating samples from noise by iteratively applying a neural network (εθ) at different timesteps (tN to t0). The AdjointDEIS part shows the backward process of computing gradients (∂x(ti)) by applying the AdjointDEIS solver. These gradients are used to optimize the initial latent representation (xN) to achieve a desired output. The number of timesteps are different for sampling (N) and AdjointDEIS (M).

This table presents the effectiveness of various face morphing attacks against three different face recognition (FR) systems. It compares the performance of several morphing techniques, including traditional methods (Webmorph, MIPGAN-I, MIPGAN-II), previous diffusion-model-based attacks (DiM-A, Fast-DiM, Morph-PIPE), and the proposed AdjointDEIS method. The results are presented in terms of MMPMR (Mated Morph Presentation Match Rate) at a 0.1% False Match Rate (FMR). The NFE (number of forward evaluations) provides a measure of the computational cost of each attack. Lower NFE values indicate a more efficient attack, while higher MMPMR values suggest greater vulnerability of the FR systems.

In-depth insights

#

AdjointDEIS: Gradient Flow

#

AdjointDEIS, in the context of gradient flow within diffusion models, presents a novel approach to efficiently compute gradients. Instead of relying on memory-intensive backpropagation, it leverages continuous adjoint equations. This method is particularly beneficial for diffusion models that utilize stochastic differential equations (SDEs), where handling injected noise during sampling adds complexity. AdjointDEIS tackles this by simplifying the continuous adjoint equations into a simple ordinary differential equation (ODE), resulting in significantly faster and more efficient gradient calculation. The use of exponential integrators further enhances this efficiency. The key contribution lies in bespoke ODE solvers tailored to the specific structure of diffusion SDEs, guaranteeing convergence order and providing a powerful technique for guided generation and optimization in diffusion models. This method showcases an advantage over traditional backpropagation techniques for various tasks that depend on gradients.

Diffusion ODE/SDE Solver

#

The core of diffusion models lies in their ability to generate data samples by reversing a diffusion process. This reversal is achieved using either an ODE (ordinary differential equation) or an SDE (stochastic differential equation) solver. Choosing between ODE and SDE solvers involves a trade-off: ODE solvers are generally faster but might not capture the full nuances of the diffusion process. SDE solvers, while slower, often provide better sample quality, particularly in high-dimensional spaces. The efficiency and accuracy of these solvers significantly impact the overall performance and scalability of diffusion models. Developing novel and efficient solvers for diffusion ODEs and SDEs, particularly ones that handle the injected noise from the diffusion term effectively, is crucial for improving the speed and quality of diffusion-based generative models. The use of continuous adjoint equations in conjunction with specially designed solvers, as discussed in the paper, promises to enhance the training process by enabling more efficient gradient calculation for model optimization. The selection of solver ultimately depends on the specific application and the desired balance between computational cost and sample quality.

Face Morphing Attacks

#

Face morphing attacks, a severe threat to facial recognition systems, involve generating synthetic images that blend features from multiple individuals. These morphed faces can deceive authentication systems, leading to identity theft, security breaches, and potentially even more serious consequences. The research paper delves into this critical area by exploring the use of diffusion models, state-of-the-art generative models, to create highly realistic face morphs. The authors propose a novel technique, AdjointDEIS, to efficiently train these models, improving the speed and quality of the morphing process. This new method tackles the computational challenges involved in optimizing such models, potentially enabling the creation of more sophisticated and harder-to-detect face morphs. The paper presents compelling experimental results on face morphing, demonstrating the technique’s potential. However, it also acknowledges the potential for misuse and advocates for responsible use of this research. The ability to create realistic morphed images necessitates further research into robust countermeasures, as such technology could have severe implications for security and privacy.

Conditional Info Schedule

#

The concept of ‘Conditional Info Schedule’ in diffusion models is crucial for controlled generation. It allows for dynamic adjustments to the guidance signal during the denoising process, unlike static conditioning. This dynamic control enables complex manipulation of the generated output by strategically varying the guidance, for example, gradually blending two different concepts or progressively focusing on specific features. Careful design of the scheduling is vital; inappropriate schedules can lead to artifacts or incoherent outputs. The timing and nature of the schedule will depend on the specific application. For instance, a linear schedule might be adequate for simple transitions, whereas a more intricate schedule might be necessary for highly detailed or intricate results. Therefore, research into optimal scheduling strategies is important for maximizing the effectiveness of this technique in image generation, text-to-image synthesis, and other diffusion model applications.

Future Research Paths

#

Future research could explore several promising directions. Extending AdjointDEIS to higher-order solvers and rigorously analyzing their convergence properties would enhance efficiency and accuracy. Investigating the application of AdjointDEIS to other diffusion model architectures beyond those studied in this paper is crucial for broader applicability. A particularly interesting area is applying AdjointDEIS to models employing different noise schedules or diffusion processes, potentially leading to even greater efficiency gains. Exploring the theoretical implications of the simplified adjoint equations for diffusion SDEs could yield new insights into the optimization landscape of diffusion models. Finally, developing robust and efficient methods for handling conditional information that changes dynamically during the generative process would significantly improve the quality and controllability of generated content.

More visual insights

#

More on figures

This figure shows a successful face morphing attack generated using the AdjointDEIS method. It visually demonstrates the technique’s ability to create a realistic-looking morphed face image (b) that combines features from two original faces (a) and (c). This illustrates the effectiveness of AdjointDEIS in guided generation for face morphing tasks. The FRLL dataset was used for this experiment.

This figure shows an example of a face morphing attack generated using the AdjointDEIS method. The top row displays the original identity image (a), followed by a sequence of morphed faces generated using the AdjointDEIS technique, and finally the target identity (b). This illustrates the algorithm’s ability to smoothly interpolate between two facial identities while maintaining a degree of realism.

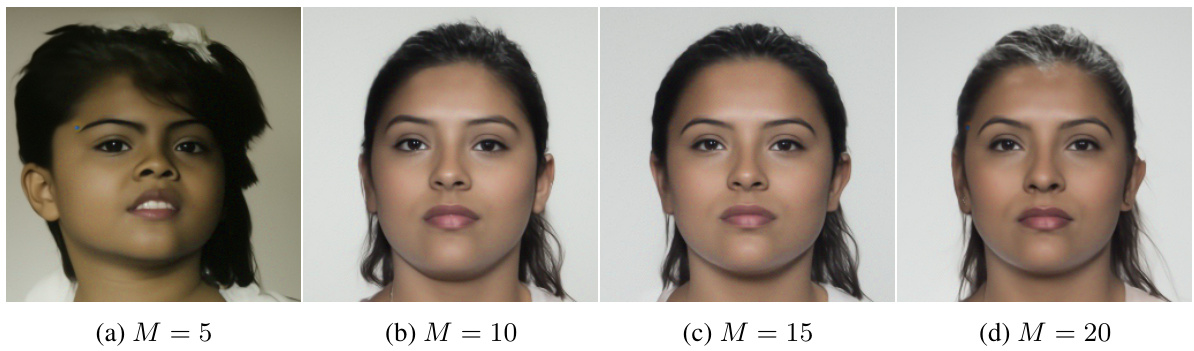
This figure shows the results of face morphing using the AdjointDEIS method with varying numbers of discretization steps (M). It demonstrates how the quality of the generated morphed face improves as the number of steps increases from 5 to 20. The figure visually represents the impact of the discretization step size on the accuracy and detail of the generated morphs.

This figure shows three morphed faces generated using the AdjointDEIS method with different learning rates (η = 0.01, η = 0.1, and η = 1). The number of discretization steps (M) was kept constant at 20, and the ODE variant of AdjointDEIS was used. The purpose is to illustrate the impact of the learning rate on the quality of the generated morphed face. A larger learning rate leads to less accurate gradients and a lower quality result.

This figure shows two morphed faces generated using the AdjointDEIS method with different numbers of sampling steps (N). The left image (a) uses N=20 steps, while the right image (b) uses N=50 steps. This illustrates the impact of the number of sampling steps on the quality and detail of the generated morphed face. More sampling steps generally lead to higher-quality results.

More on tables

This table shows the impact of the number of discretization steps (M) used in the AdjointDEIS algorithm on the performance of face morphing attacks. The results are measured by the MMPMR metric (Mated Morph Presentation Match Rate) at a False Match Rate (FMR) of 0.1% across three different Face Recognition (FR) systems: AdaFace, ArcFace, and ElasticFace. As the number of discretization steps decreases, the performance of the morphing attack also decreases. This indicates that using a sufficient number of steps in the AdjointDEIS solver is crucial for achieving high performance in generating effective morphed faces.

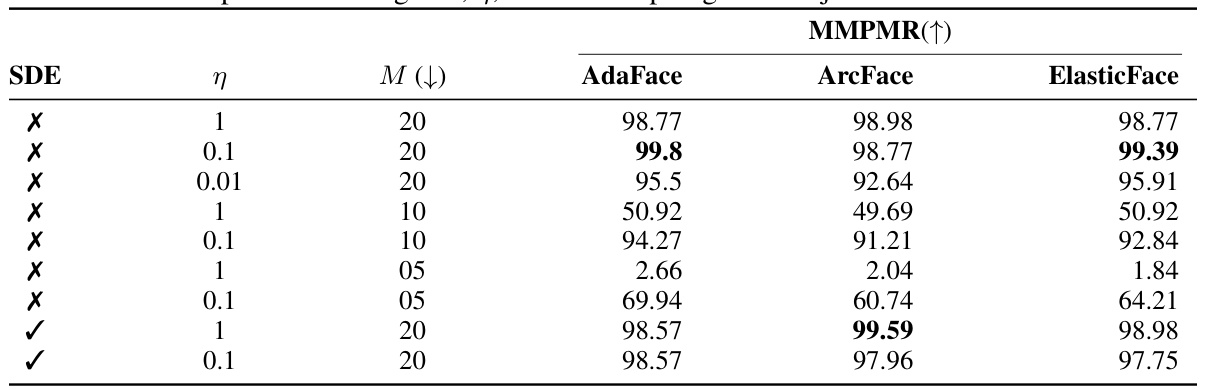
This table presents the results of experiments evaluating the effect of different learning rates (η) on the performance of the AdjointDEIS method for face morphing. It shows the MMPMR (Mated Morph Presentation Match Rate) achieved using different learning rates with varying numbers of discretization steps (M) for both ODE and SDE variants of the AdjointDEIS algorithm. A higher MMPMR indicates better performance in creating successful morphs. The False Match Rate (FMR) was kept constant at 0.1%.

This table compares several training-free guided diffusion methods. The comparison is based on whether each method solves for diffusion ODEs or SDEs, optimizes the initial latent state (xT), and/or optimizes the conditional information (z, θ). It highlights the differences in approach and capabilities among various techniques.

This table compares AdjointDPM and AdjointDEIS methods by highlighting key differences in their discretization domain (whether they operate over (\rho) or (\lambda)), solver type (black box ODE solver vs. custom solver), handling of closed-form SDE coefficients, interoperability with existing samplers, decoupled ODE schedules, and support for SDEs. AdjointDEIS offers advantages in several aspects, including its use of custom solvers and support for SDEs.

Full paper

#