TL;DR#
High-dimensional data analysis often faces challenges due to storage and computational costs. Existing methods, like random projection, tackle this by reducing data dimensionality, but often lead to significant information loss and suboptimal storage efficiency. The paper focuses on improving approximate nearest neighbor search, where preserving relative distances between data points is key, but reducing the bit size of data is also crucial. The main issue addressed is how to better compress point sets to minimize storage space without excessive information loss, particularly for applications requiring high accuracy in distance approximation.
The researchers propose a novel nonlinear compression method using deep random features (a composition of multiple random feature mappings). They rigorously prove that, under certain conditions, this approach requires fewer bits than linear methods for preserving pairwise distances up to a small error. The method maps data points directly to a discrete cube, thus eliminating the extra step of converting sketches into bits for storage. Experiments with synthetic and real-world datasets demonstrate that this method outperforms existing techniques for a specific range of distances and parameters, suggesting its potential value for applications where high-accuracy, compact representations are crucial.
Key Takeaways#
Why does it matter?#
This paper is significant as it presents a novel method for compressing high-dimensional datasets while preserving crucial distance information, a critical need in various data analysis applications. It offers a unique nonlinear approach which outperforms linear methods in certain scenarios, opening new avenues in data storage and efficient similarity search. Its findings could directly impact diverse fields, making it highly relevant to researchers working in dimensionality reduction, nearest neighbor search, and efficient data representation.
Visual Insights#

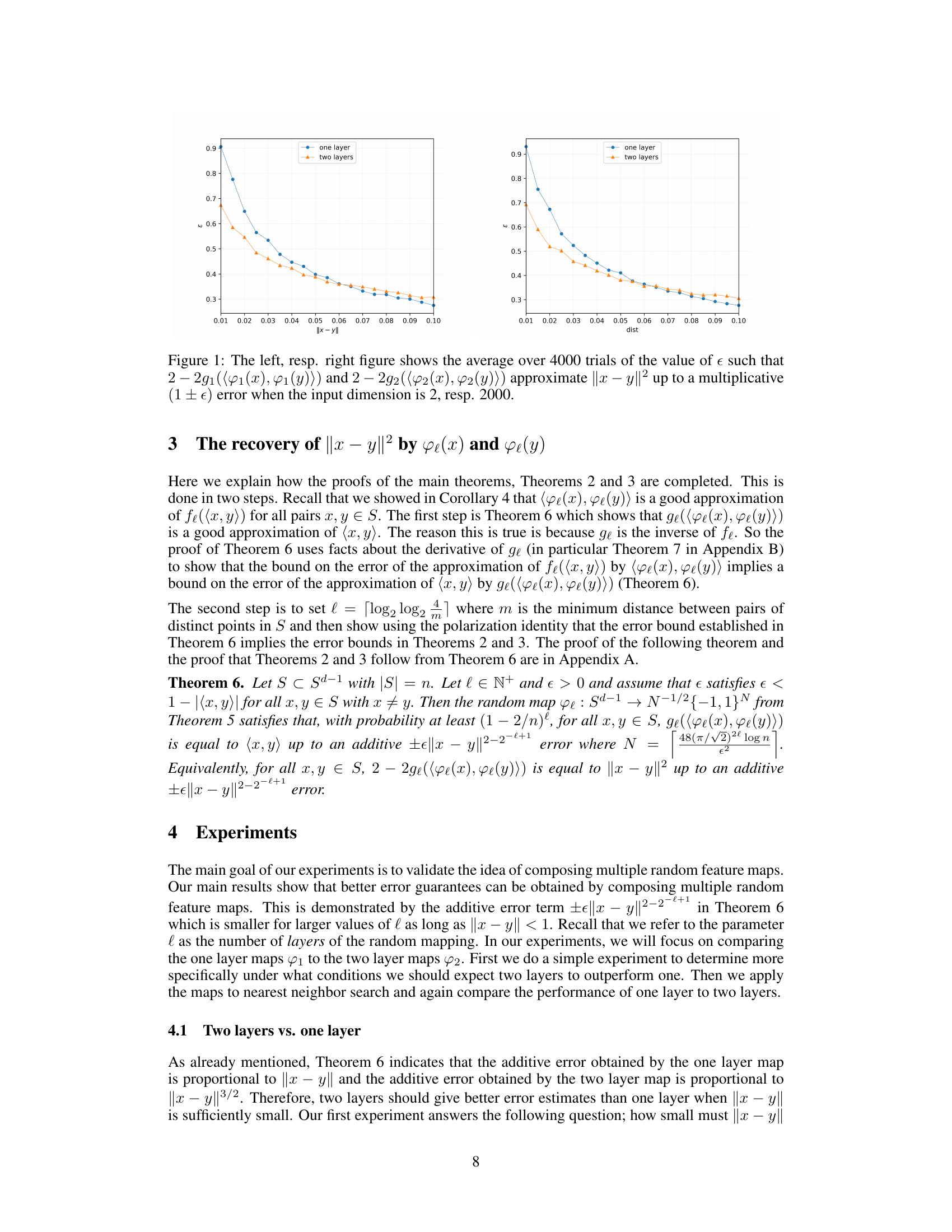
🔼 This figure compares the performance of one-layer and two-layer random feature maps in approximating pairwise squared distances. The left panel shows the results for a 2-dimensional input space, while the right panel shows results for a much higher dimensional input space (2000). The x-axis represents the true squared distance between pairs of points, and the y-axis represents the multiplicative error such that the approximated squared distance is within (1±) of the true value. The results are averages over 4000 trials.
read the caption
Figure 1: The left, resp. right figure shows the average over 4000 trials of the value of such that 2 – 2g1((φ1(x), φ1(y))) and 2 – 2g2((φ2(x), φ2(y))) approximate ||x − y||2 up to a multiplicative (1 ± ) error when the input dimension is 2, resp. 2000.
In-depth insights#
Deep Random Feat.#
The heading ‘Deep Random Feat.’ likely refers to a novel method using deep learning combined with random projections for dimensionality reduction. This approach combines the strengths of both techniques: the ability of random projections to preserve distances while reducing dimensionality, and the capacity of deep learning models to learn complex, non-linear mappings. The ‘deep’ aspect suggests multiple layers in the architecture, potentially improving approximation accuracy of distances in the compressed space. A key advantage may be the potential to map data directly into a discrete representation (like a binary code), simplifying storage and reducing computational costs. However, challenges may include increased computational complexity during training of the deep network and the careful selection of network architecture and hyperparameters to balance performance and computational efficiency. The success of this method depends on whether it can achieve comparable or better performance compared to existing dimensionality reduction techniques, while offering advantages in terms of space or time complexity.
Bit-efficient Sketch#
Bit-efficient sketching techniques are crucial for managing high-dimensional data, especially when storage and computational resources are limited. The core idea is to represent a dataset with a smaller sketch that preserves key information like pairwise distances, while minimizing the number of bits required. Random projections are often used, but they may not be optimal in terms of bit efficiency. New approaches, such as those using deep random features, aim to improve upon this by leveraging nonlinear mappings that directly project data into a discrete space (like the hypercube), bypassing the need for additional quantization steps. These methods demonstrate improvements in bit-efficiency in certain scenarios, particularly when the distances between points are not uniformly distributed. However, limitations exist; the efficiency gains depend on data characteristics and the choice of parameters. Further exploration of bit-efficient sketches could explore new mappings, error-correcting codes and adaptive quantization strategies to develop sketches suitable for various real-world applications.
Nonlinear Map#
The concept of a “Nonlinear Map” in the context of this research paper likely refers to a function that transforms data points in a non-linear fashion, mapping high-dimensional data to a lower-dimensional space. Unlike linear dimensionality reduction techniques (like PCA), nonlinear maps can capture more complex relationships and structures within the data. The paper explores the use of such maps, potentially to compress high-dimensional point sets while preserving key information about their Euclidean distances. This compression is achieved by cleverly designed compositions of random feature mappings, creating a deep neural-network-like architecture. The theoretical contribution likely focuses on proving that these carefully constructed nonlinear maps achieve the desired level of compression and accuracy with high probability, offering advantages over existing methods. The choice of nonlinearity and its composition are crucial to maintaining accuracy and reducing the bit representation of the sketch. Experimental evaluation likely demonstrates the effectiveness of this approach in tasks such as nearest neighbor search, comparing its performance and storage requirements to both linear and other nonlinear compression methods.
NN Search App.#
The heading ‘NN Search App.’ suggests an application of the research paper’s core methodology to nearest neighbor (NN) search. This is a significant application area because NN search is computationally expensive in high dimensions. The paper likely demonstrates how their proposed method, possibly involving deep random features for Euclidean distance compression, improves the efficiency of NN search. Key aspects to consider include the algorithm’s scalability, its ability to handle high-dimensional data, and a comparison of its performance against existing NN search algorithms or techniques. The results may show a reduction in computational complexity or storage requirements, potentially making NN search feasible for larger datasets or higher dimensions than previously possible. Specific metrics for evaluation would likely include search time, accuracy (precision and recall), and the overall effectiveness in finding true nearest neighbors. The application section would likely showcase experimental results on benchmark datasets, illustrating the practical benefits of the proposed compression method in an NN search context. Analyzing this section critically requires attention to dataset selection, evaluation metrics, and comparison against appropriate baselines to assess the true performance gains.
Future Directions#
Future research could explore several promising avenues. Improving the efficiency of the deep random feature maps is crucial, potentially through algorithmic optimizations or exploring alternative architectures. Extending the theoretical analysis to a broader range of datasets beyond those on or near the unit sphere is needed, along with relaxing constraints on the minimum pairwise distance. Investigating the impact of different activation functions and their interaction with the number of layers could enhance the accuracy and efficiency. Finally, applications to other machine learning tasks that leverage approximate distance information, such as clustering or dimensionality reduction, warrant further exploration. The potential impact is significant, with the capacity for improved speed and storage efficiency in many machine learning applications.
More visual insights#
More on figures
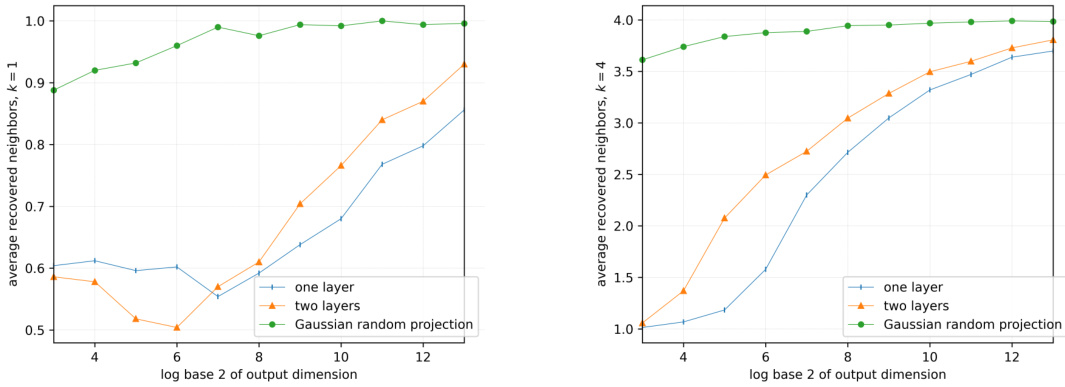
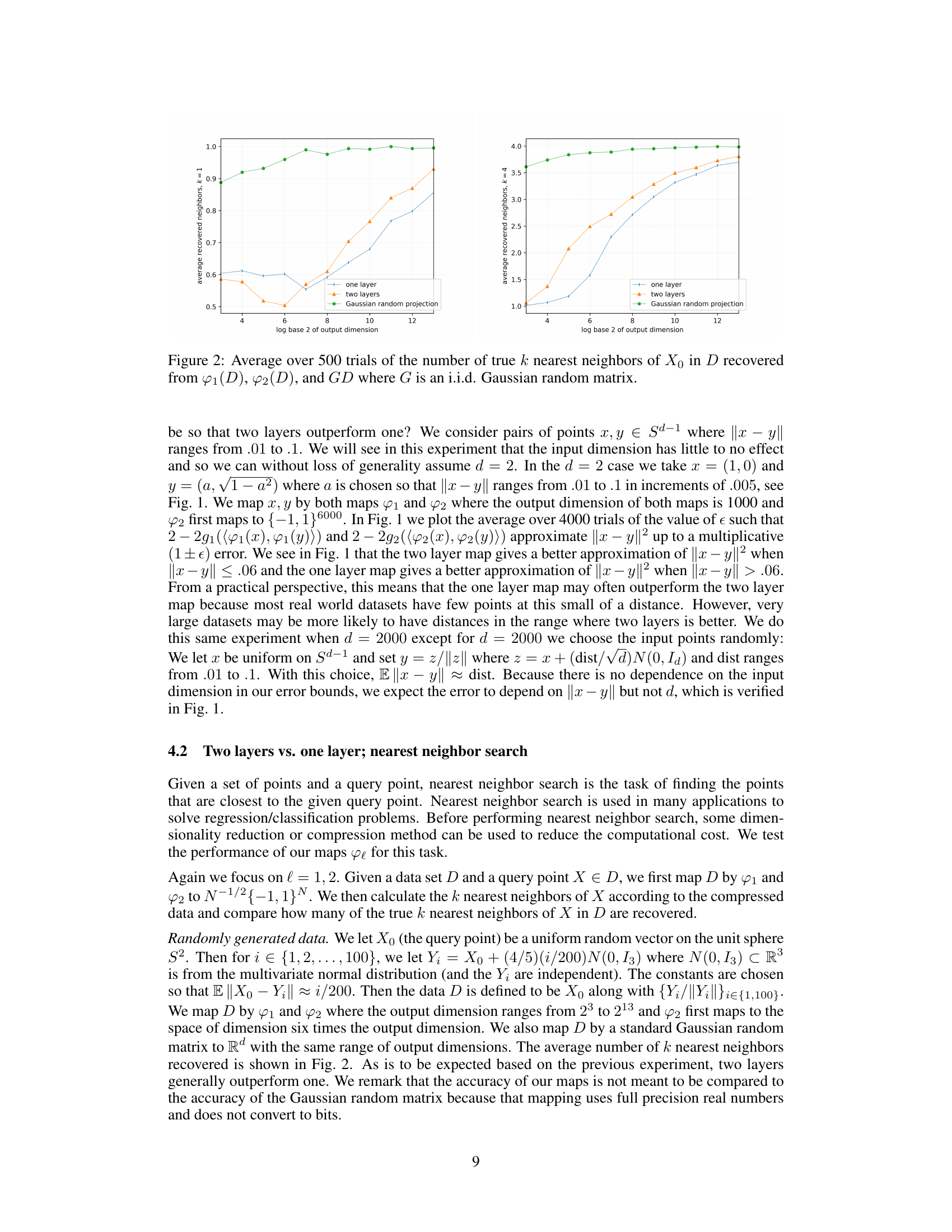
🔼 The figure shows the result of an experiment to compare the performance of one-layer and two-layer random feature maps to a standard Gaussian random projection for nearest neighbor search. The x-axis represents the output dimension (log base 2). The y-axis shows the average number of true k-nearest neighbors recovered. The experiment uses randomly generated data and evaluates performance for k=1 and k=4.
read the caption
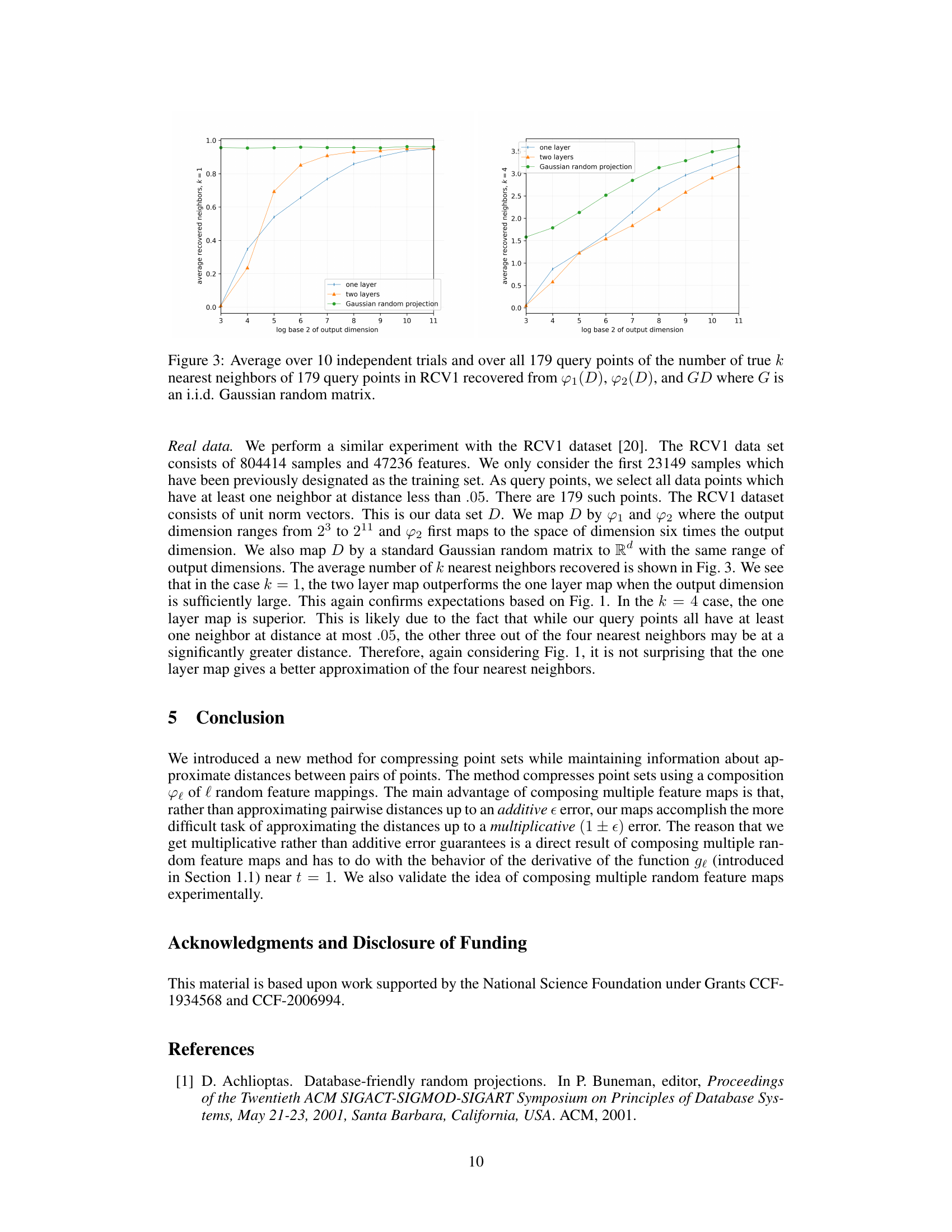
Figure 2: Average over 500 trials of the number of true k nearest neighbors of X0 in D recovered from φ1(D), φ2(D), and GD where G is an i.i.d. Gaussian random matrix.

🔼 This figure shows the result of an experiment to compare the performance of one-layer and two-layer random feature maps for nearest neighbor search. The experiment uses randomly generated data in 3 dimensions. For each output dimension, 500 trials were conducted and the average number of correctly recovered nearest neighbors was calculated for both one-layer and two-layer maps. The results are compared to a standard Gaussian random projection. The experiment considers k=1 and k=4 nearest neighbors.
read the caption
Figure 2: Average over 500 trials of the number of true k nearest neighbors of X0 in D recovered from φ1(D), φ2(D), and GD where G is an i.i.d. Gaussian random matrix.
Full paper#