TL;DR#
Current large language models (LLMs) utilize chain-of-thought prompting to enhance reasoning capabilities. However, the performance of these models significantly degrades when presented with noisy rationales (Noisy-R), which contain irrelevant or inaccurate reasoning steps. This paper addresses the challenges of noisy rationales. Existing robust methods like self-correction and self-consistency show limited efficacy.
To tackle the problem, this paper proposes a novel method, Contrastive Denoising with Noisy Chain-of-Thought (CD-CoT), which enhances LLMs’ denoising-reasoning capabilities by contrasting noisy rationales with a clean one. CD-CoT demonstrates improved accuracy and denoising capabilities compared to existing methods. The authors provide the NoRa dataset to evaluate LLM reasoning robustness under noisy rationales.
Key Takeaways#
Why does it matter?#
This paper is crucial because it reveals a significant vulnerability of LLMs to noisy rationales in chain-of-thought prompting, a widely used technique in AI. It introduces a new dataset and method to address this, opening new avenues for research on LLM robustness and reliability and influencing the development of more trustworthy AI systems.
Visual Insights#

🔼 This figure shows examples of noisy questions and noisy rationales used in the paper’s experiments. The left-hand side demonstrates examples where the provided context includes irrelevant information (base-10 arithmetic) that is not relevant to solving the actual base-9 math problem. The right-hand side displays examples where the rationales contain irrelevant or inaccurate reasoning steps, again interfering with the correct solution of the base-9 problem. Both illustrate the challenges posed by noisy data in chain-of-thought prompting.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

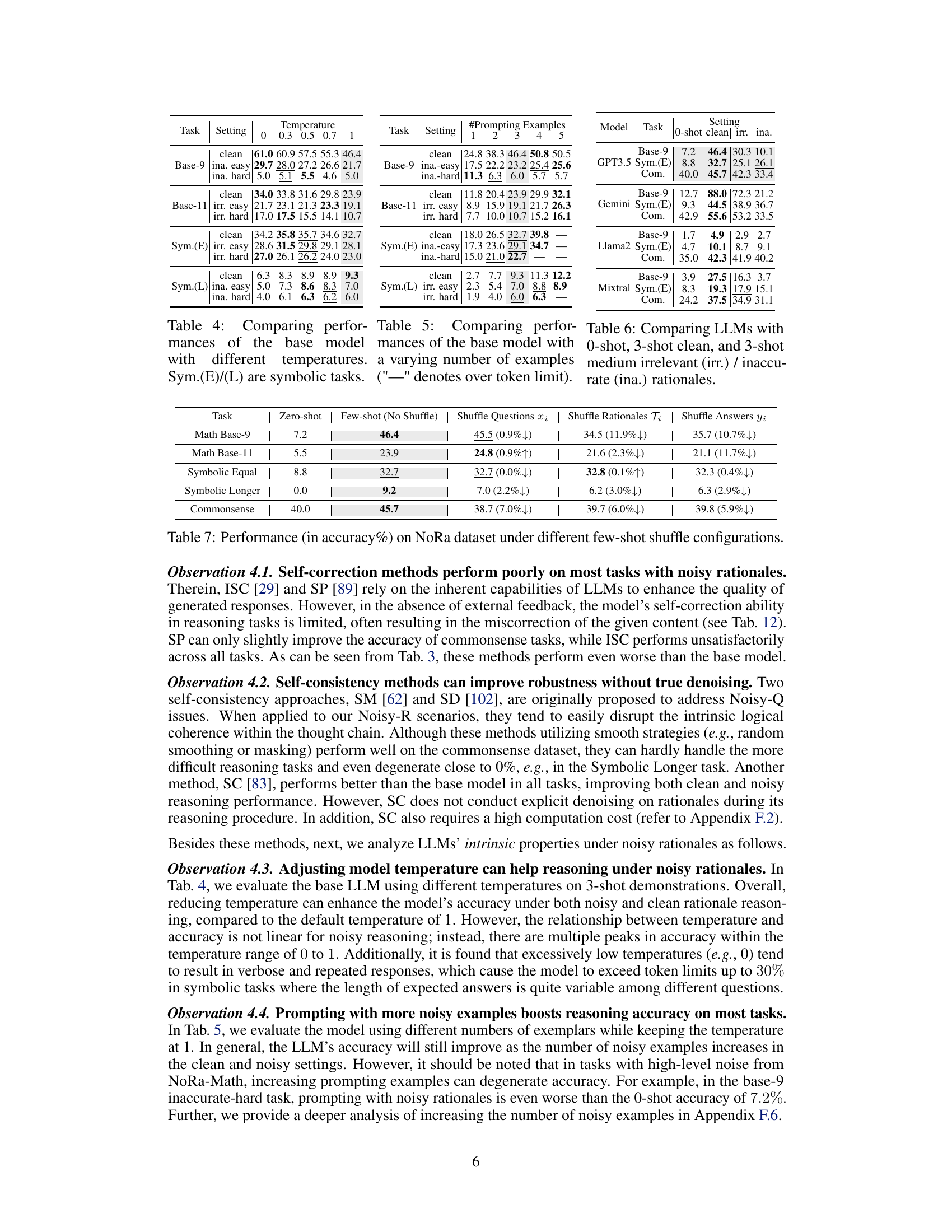
🔼 This table presents the accuracy results of different LLMs (GPT-3.5, and others) on the NoRa dataset. It shows accuracy scores under three different conditions: clean rationales, irrelevant rationales, and inaccurate rationales for three difficulty levels (easy, medium, hard). The results reveal how well each model performs in the presence of noisy rationales (irrelevant or inaccurate reasoning steps). Base models and models with various robustness methods are compared for analysis. The bold numbers highlight the highest accuracies for each condition.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
In-depth insights#
Noisy Rationale Problem#
The “Noisy Rationale Problem” highlights a critical weakness in chain-of-thought prompting for large language models (LLMs). Noisy rationales, containing irrelevant or inaccurate reasoning steps within training examples, significantly hinder LLM performance. This contrasts with the common focus on noisy questions, demonstrating that rationale quality is equally crucial for reliable reasoning. The problem’s practical relevance stems from the prevalence of noisy rationales in real-world datasets, including crowd-sourced and automatically generated data. Existing robustness methods such as self-correction and self-consistency show limited effectiveness against noisy rationales, underscoring the need for new approaches. The challenge demands external supervision, but this must be readily available and minimally intrusive. This issue necessitates further research into robust methods and better dataset creation practices to address the inherent fragility of LLMs to noisy rationales within the chain-of-thought framework.
CD-CoT Method#
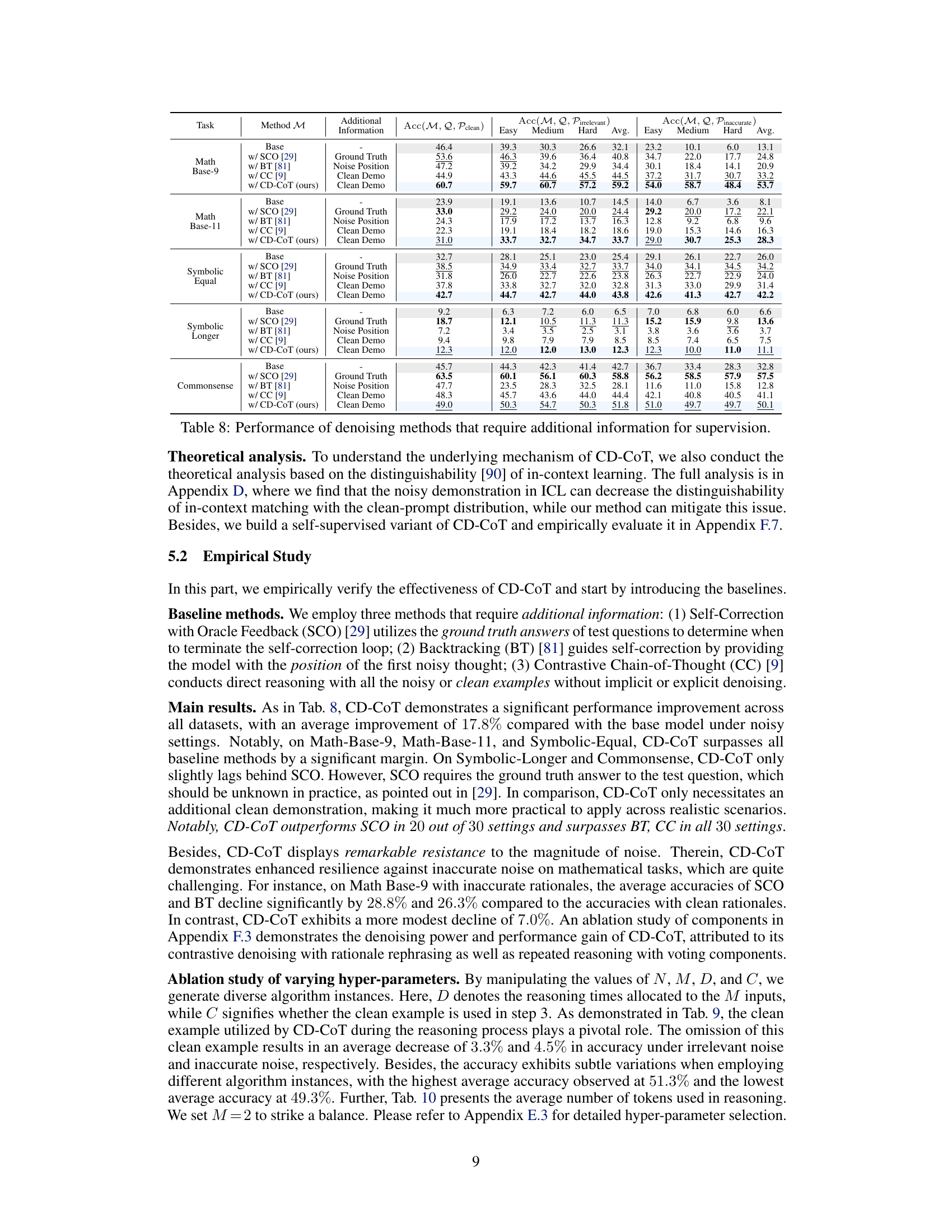
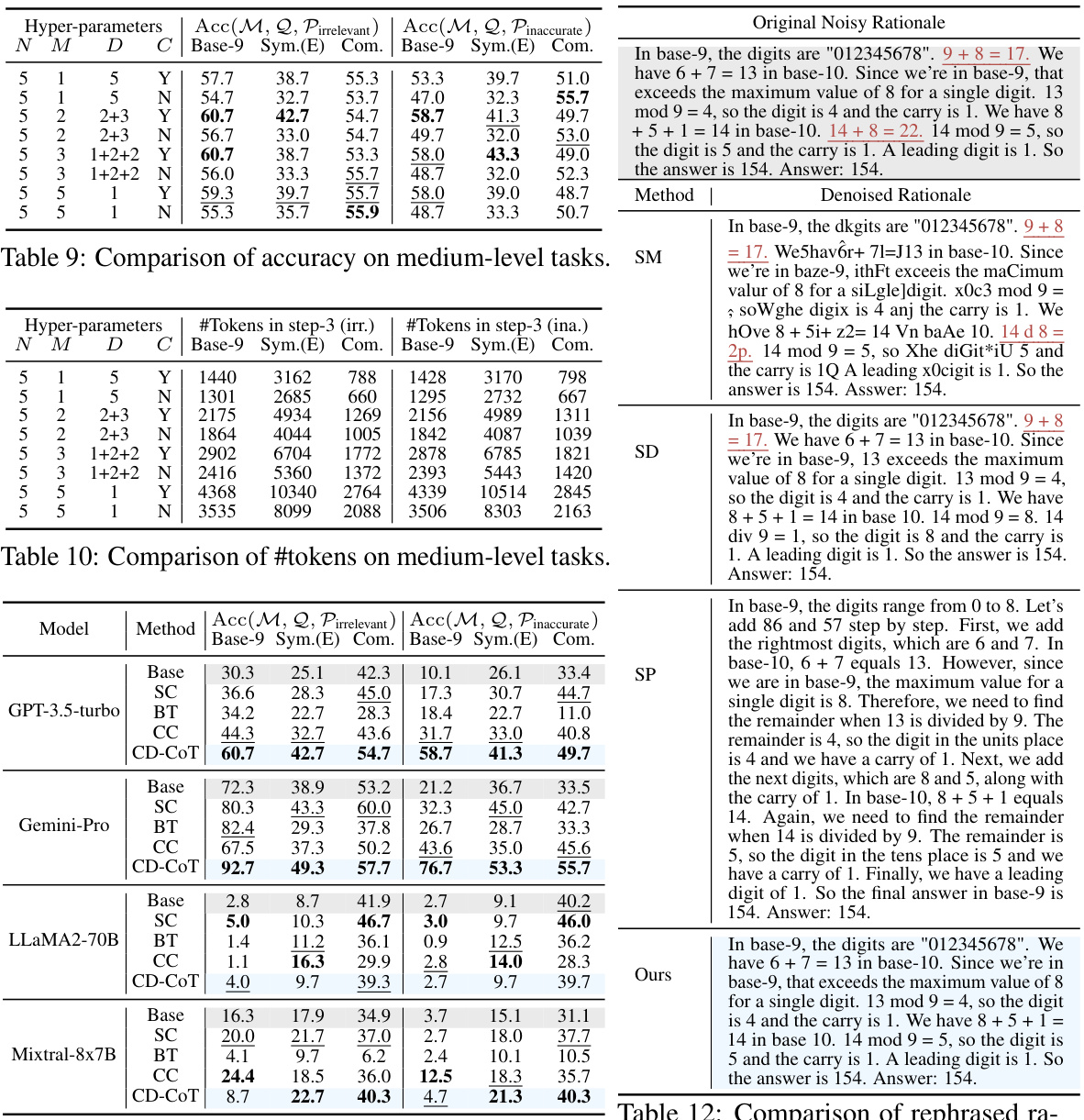
The core of this research paper revolves around a novel method called CD-CoT (Contrastive Denoising with noisy Chain-of-Thought), designed to enhance the robustness of large language models (LLMs) when faced with noisy rationales during chain-of-thought prompting. CD-CoT tackles the challenge of noisy rationales by employing a contrastive learning approach. Instead of relying solely on the LLM’s intrinsic denoising capabilities, which prove limited in the presence of noise, CD-CoT leverages the availability of at least one clean rationale example. This clean example is used as a baseline for comparison against noisy rationales, allowing the model to discern and rectify irrelevant or inaccurate reasoning steps. The method involves a multi-step process: rephrasing noisy rationales, selecting the most promising candidates, exploring diverse reasoning paths, and ultimately voting on the most likely answer. This approach, grounded in a principle of exploration and exploitation, allows CD-CoT to significantly improve upon baselines methods, demonstrating enhanced denoising and reasoning capabilities, and achieving an average improvement of 17.8% in accuracy.
LLM Robustness#
The research explores Large Language Model (LLM) robustness, particularly focusing on chain-of-thought prompting’s vulnerability to noisy rationales. The core finding reveals a significant performance drop in LLMs when presented with examples containing irrelevant or inaccurate reasoning steps. This highlights a critical gap in current research, as most studies assume clean demonstrations. The study introduces NoRa, a comprehensive benchmark dataset tailored to evaluate this robustness against various reasoning tasks and noise levels. The findings demonstrate that existing robust methods, like self-correction and self-consistency, offer limited efficacy against the challenges posed by noisy rationales. This necessitates external supervision, leading to the proposal of CD-CoT, a contrastive denoising method significantly improving LLM performance in noisy scenarios. CD-CoT leverages the contrast between noisy and clean rationales to enhance LLMs’ ability to denoise and reason effectively. The research also analyzes the impact of different noise types and levels, and the number of noisy examples on model performance, uncovering valuable insights into the inherent vulnerabilities of LLMs. The study concludes by emphasizing the need for further research to improve LLM robustness, suggesting the exploration of external knowledge bases and multi-modal data integration.
Noisy Rationale Dataset#
A Noisy Rationale dataset is a valuable resource for evaluating the robustness of large language models (LLMs). It addresses a critical gap in existing benchmarks by focusing on the quality of the rationales, or intermediate reasoning steps, within prompting examples. Unlike datasets focused solely on noisy inputs or outputs, this dataset allows researchers to specifically assess LLMs’ ability to handle irrelevant or inaccurate reasoning steps embedded within otherwise correctly formatted prompts. This is crucial because real-world data often contains such noise, making the ability to filter and correct for such noise a key aspect of reliable LLM performance. The dataset’s design, which allows for controlled introduction of noise into rationales, enables nuanced analysis of LLMs’ strengths and weaknesses in handling noisy rationales. Such insights are vital for enhancing LLM robustness and developing effective countermeasures against the detrimental effects of noisy data. The creation of this type of dataset also highlights the importance of carefully considering not just the correctness of input and output but also the quality and reliability of the intermediate steps in the reasoning process used by LLMs.
Future Work#
Future research could explore several promising avenues. Improving the robustness of LLMs against noisy rationales is paramount, potentially through techniques like contrastive learning or incorporating external knowledge bases. Developing self-supervised methods that reduce reliance on clean rationale annotations would significantly enhance practicality. Exploring diverse prompting strategies and investigating their impact on model performance under noisy conditions could yield valuable insights. Expanding the NoRa dataset to encompass more diverse reasoning tasks and modalities (such as incorporating visual data) is vital to broaden the evaluation scope and better reflect real-world scenarios. Finally, further theoretical analysis of the inherent vulnerabilities of LLMs under noisy rationales is needed to guide the development of more robust algorithms and architectures.
More visual insights#
More on figures

🔼 This figure displays the accuracy achieved by GPT-3.5 across three different prompting scenarios: zero-shot (no examples), three clean examples, and three examples with noisy rationales. The noisy examples were further divided into two categories: those containing irrelevant information and those with inaccurate information. The results clearly demonstrate that noisy rationales significantly reduce the accuracy of GPT-3.5. The introduction of irrelevant information reduces accuracy by 1.4%-19.8% compared to the clean examples, while inaccurate information causes a much more significant drop, of 2.2%-40.4%. In contrast, the proposed CD-CoT method shows significant improvement in robustness against noisy rationales.
read the caption
Figure 2: Results of GPT-3.5 with 0-shot, 3-shot clean rationales, and 3-shot noisy rationales: Both inaccurate and irrelevant rationales degenerate performance significantly, while the proposed CD-CoT improves robustness against noisy rationales.

🔼 This figure illustrates the chain-of-thought (CoT) process with noisy rationales. It shows how a language model can recover a clean chain of reasoning (chain 1) from a noisy chain (chain 3) by using a clean chain (chain 2) as guidance. Chain 3 contains both clean (T(i)) and noisy thoughts (f(i)). The model learns to separate clean and noisy reasoning steps from the examples to get the correct answers.
read the caption
Figure 3: Chain modeling of the noisy rationale problem: Recovering chain (3) from chain (1) with the guidance of chain (2). From question Xi to answer yi, the rationale of chain (3) includes clean thoughts T() and noisy thoughts (i).

🔼 This figure shows examples of the two types of noisy inputs used in the Noisy Rationales dataset. The left side demonstrates noisy questions that include irrelevant or inaccurate base-10 information, while the right side shows noisy rationales that contain irrelevant or inaccurate reasoning steps, both leading to incorrect solutions in a base-9 calculation problem.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of both noisy questions and noisy rationales. The noisy questions contain irrelevant information (base-10 calculations) which is misleading when the test question is actually about base-9. The noisy rationales include irrelevant or inaccurate reasoning steps within the otherwise correct examples. This highlights the core problem that the paper investigates: how robust are large language models when prompted with noisy rationales in a chain-of-thought prompting setting?
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples from the NoRa dataset, highlighting the difference between inputs with clean rationales and inputs with noisy rationales. The noisy rationales contain irrelevant or inaccurate reasoning steps. The examples illustrate the challenge of chain-of-thought prompting when dealing with noisy rationales. Each input consists of three examples and a test question, focusing on base-9 calculation.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of noisy questions and rationales used in the paper’s experiments. The top half shows examples with noisy questions where irrelevant base-10 information is included alongside a base-9 calculation problem. The bottom half shows examples with noisy rationales, where irrelevant or inaccurate reasoning steps are presented within the example rationales, still leading to the correct answer. The goal is to evaluate how well large language models handle these types of noisy inputs when using chain-of-thought prompting.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of noisy questions and rationales used in the paper. Each example includes three question-rationale-answer triplets followed by a test question. The noisy examples contain irrelevant or inaccurate reasoning steps (rationales) that are designed to mislead the language model. The test question, however, is similar in structure to the examples, allowing for an evaluation of the model’s robustness to noisy rationales. The example illustrates a math problem involving base-9 arithmetic, yet the provided rationales mistakenly include calculations based on base-10, demonstrating the concept of noisy rationales.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows the performance of GPT-3.5 language model on the NoRa dataset under different conditions. The 0-shot results (no examples) show a baseline. The ‘Clean’ bars show performance when the model is prompted with three examples with correct rationales. ‘Irrelevant’ and ‘Inaccurate’ bars show performance when noisy rationales (irrelevant or inaccurate reasoning steps) are present in the examples. The figure shows that both irrelevant and inaccurate rationales lead to lower accuracy. The bars labeled ‘Irrelevant (with CD-CoT)’ and ‘Inaccurate (with CD-CoT)’ demonstrate the improvement in accuracy achieved by the proposed CD-CoT method, which is designed to improve robustness against noisy rationales.
read the caption
Figure 2: Results of GPT-3.5 with 0-shot, 3-shot clean rationales, and 3-shot noisy rationales: Both inaccurate and irrelevant rationales degenerate performance significantly, while the proposed CD-CoT improves robustness against noisy rationales.

🔼 This figure shows the accuracy of GPT-3.5 on three different tasks from the NoRa dataset. The accuracy is shown for three different conditions: 0-shot (no examples), 3-shot with clean rationales, and 3-shot with noisy rationales (both irrelevant and inaccurate). The results show that the presence of noisy rationales significantly decreases the accuracy of GPT-3.5, while the proposed CD-CoT method improves the robustness of the model to noisy rationales.
read the caption
Figure 2: Results of GPT-3.5 with 0-shot, 3-shot clean rationales, and 3-shot noisy rationales: Both inaccurate and irrelevant rationales degenerate performance significantly, while the proposed CD-CoT improves robustness against noisy rationales.

🔼 This figure displays the performance of GPT-3.5 under different prompting conditions. The x-axis shows four different categories: 0-shot, clean rationales, irrelevant rationales and inaccurate rationales. Each bar represents the average accuracy across multiple reasoning tasks. The results indicate a significant drop in accuracy when using noisy rationales compared to clean rationales. The proposed CD-CoT method shows improved robustness to noisy rationales.
read the caption
Figure 2: Results of GPT-3.5 with 0-shot, 3-shot clean rationales, and 3-shot noisy rationales: Both inaccurate and irrelevant rationales degenerate performance significantly, while the proposed CD-CoT improves robustness against noisy rationales.

🔼 This figure shows examples of noisy questions and rationales used in the paper’s experiments. The left side shows a standard prompt with clean questions and rationales while the right side shows a prompt with noisy rationales. Noisy rationales include irrelevant or factually incorrect information that is designed to mislead large language models (LLMs). The examples shown are addition problems in base 9; however, the rationales include unnecessary information from base 10 calculations that are designed to confuse the model. This highlights the core research challenge of the paper; demonstrating the impact of noisy rationales on LLM performance.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of noisy questions and noisy rationales. The left side displays examples with noisy questions containing irrelevant information about base-10 calculations, while the right side shows examples with noisy rationales. Both types of noise are designed to mislead the model, while maintaining a correct final answer. The aim is to test the robustness of large language models when faced with these types of noisy input. Each example includes three prompting examples and one test question which requires base-9 calculation.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of noisy questions and noisy rationales used in the paper. The examples are designed to highlight the challenge of robust reasoning in chain-of-thought prompting when the provided rationale contains irrelevant or inaccurate information. Each example consists of three question-rationale-answer triplets followed by a test question. The test questions are all base-9 calculations, while the examples in the noisy questions and rationales include extraneous and misleading base-10 information, making it challenging for language models to correctly solve the test questions.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of both noisy questions and noisy rationales. The top half demonstrates examples with noisy questions, where extra information about base-10 calculations is included, even though the task is to solve a problem in base-9. The bottom half shows examples with noisy rationales, where incorrect or irrelevant reasoning steps are provided within the solution. In both scenarios, this extra information is meant to make it more difficult for a language model to determine the correct answer to the base-9 question.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of noisy questions and noisy rationales used in the paper’s experiments. The left side shows examples with noisy questions (containing irrelevant base-10 information, while the questions themselves are about base-9 calculations). The right side shows examples with noisy rationales (containing irrelevant or inaccurate reasoning steps). The purpose is to demonstrate the type of noisy data the language models are tested on.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of both noisy questions and noisy rationales. The noisy questions contain irrelevant or inaccurate information that can mislead the model. The noisy rationales also contain irrelevant or inaccurate reasoning steps in the chain of thought, which can also cause the model to give wrong answers. The examples shown involve base-9 arithmetic, where the presence of base-10 information acts as noise. The figure highlights the problem of robust reasoning under noisy conditions, which is the core problem addressed in the paper.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of noisy questions and noisy rationales, which are the focus of the paper. The top half displays examples where the input questions contain irrelevant base-10 information while the problem to be solved is actually in base-9. The bottom half shows examples where the rationales (reasoning steps) provided are noisy, including both irrelevant and inaccurate information, although they still lead to the correct answer. This highlights the challenge the authors address: how to make language models robust to noisy rationales during chain-of-thought prompting.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.

🔼 This figure shows examples of noisy questions and noisy rationales used in the paper’s experiments. It highlights the difference between inputs with clean questions/rationales and those with noisy ones, where irrelevant or incorrect information is added to the rationales. This illustrates the core challenge the paper addresses: how well language models perform when the training examples (demonstrations) contain noisy rationales.
read the caption
Figure 1: Exemplars of noisy questions [68] and noisy rationales (our new research problem). Each input includes three prompting examples and one test question. Notably, the test question asks about base-9 calculation, while the misguiding base-10 information is given in noisy questions or rationales.
More on tables
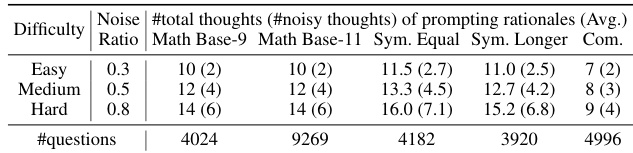
🔼 This table presents the statistics of the NoRa dataset, categorized by task difficulty (Easy, Medium, Hard) and noise ratio (0.3, 0.5, 0.8). It shows the average number of total thoughts and noisy thoughts within the prompting rationales for each task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense) and the number of questions in each category.
read the caption
Table 2: Statistics of NoRa dataset.
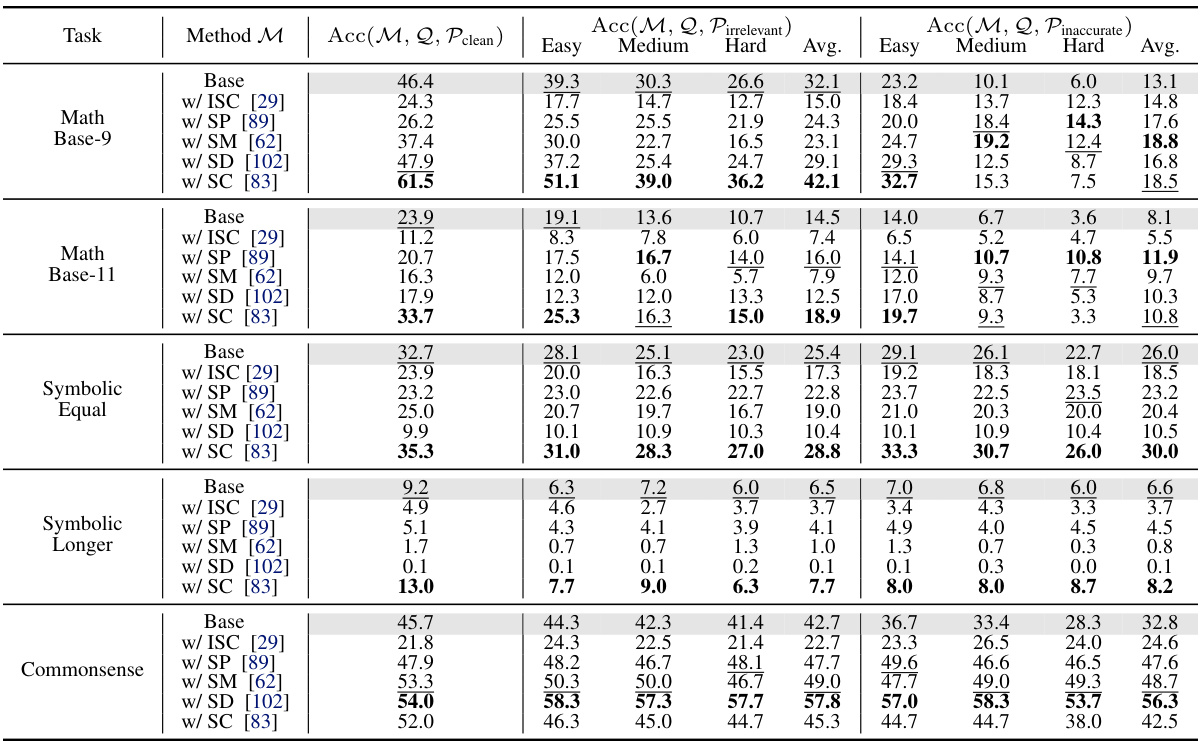
🔼 This table presents the accuracy results of different language models and robust methods on the NoRa dataset. It compares the performance using 3-shot prompting examples with clean rationales, irrelevant rationales (noise), and inaccurate rationales (noise). The table highlights the best and second-best performance for each model and noise condition, and the base model’s performance is shown in gray for comparison.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
🔼 This table presents the accuracy results of several LLMs and reasoning methods on the NoRa dataset, broken down by task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense) and noise type (clean, irrelevant, inaccurate). The table shows the accuracy of each model under each condition (Base model, various robustness methods). The best accuracy for each condition is bolded, and the second-best is underlined. The gray highlighting indicates baseline performance using the base model. This allows comparison of the impact of different noise types on model performance and the effectiveness of different robustness techniques.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the performance of language models on the NoRa dataset under various few-shot shuffle configurations. The configurations involve shuffling the questions (xi), rationales (Ti), or answers (yi) within the prompting examples. The table shows the accuracy (%) for each task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense) under each shuffle configuration, along with the percentage change compared to the ‘Few-shot (No Shuffle)’ condition. This allows for assessing the impact of shuffling different components of the prompting examples on model performance, revealing whether LLMs rely heavily on the exact mappings between questions, rationales, and answers.
read the caption
Table 7: Performance (in accuracy%) on NoRa dataset under different few-shot shuffle configurations.
🔼 This table presents the accuracy results of several LLMs and reasoning methods on the NoRa dataset. The accuracy is evaluated under three different conditions: clean rationales, irrelevant rationales, and inaccurate rationales. For each condition, the accuracy is reported for different difficulty levels (easy, medium, hard) across three tasks: mathematical reasoning, symbolic reasoning and commonsense reasoning. The best and second best results are highlighted for each task and condition. The baseline performance of the base LLM (without additional methods) is also shown in gray.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
🔼 This table presents the accuracy of several LLMs and reasoning methods on the NoRa dataset when using 3-shot prompting examples with clean, irrelevant, and inaccurate rationales. The results show the performance of a baseline model and several methods aimed at improving robustness against noisy rationales, assessing their effectiveness across different types of noise and difficulty levels. The bold numbers represent the best performance for each condition, and underlined numbers indicate the second-best.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy results of several LLMs on the NoRa dataset using different types of rationales (clean, irrelevant, and inaccurate) in 3-shot prompting experiments. It compares the performance of a base LLM (GPT-3.5-turbo) with several other LLMs and methods designed to enhance robustness (ISC, SP, SM, SD, SC) against noisy rationales across three different tasks (Math, Symbolic, Commonsense). The accuracy is shown separately for easy, medium, and hard difficulty levels for each type of rationale, and the average accuracy across all difficulty levels is also provided. Bold numbers highlight the best performance among the compared methods.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy of various LLMs and reasoning methods on the NoRa dataset when using 3-shot prompting examples with different types of rationales (clean, irrelevant, and inaccurate). The results are categorized by task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense), difficulty level (Easy, Medium, Hard), and method. The best and second-best accuracy results for each setting are highlighted in bold and underlined, respectively, and the base model accuracy is highlighted in gray to facilitate comparison. The table allows for an assessment of the robustness of different LLMs and reasoning strategies to noisy rationales.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
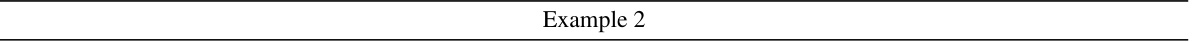
🔼 This table presents the accuracy results of various language models and reasoning methods on the NoRa dataset. It shows the performance under three conditions: clean rationales, irrelevant rationales, and inaccurate rationales, across three difficulty levels (easy, medium, hard) for each of the three reasoning tasks (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense). The best-performing method for each condition is highlighted in bold, while the second-best is underlined. The results for the base model (without any additional method) are shown in gray for comparison.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy results of several LLMs and reasoning methods on the NoRa dataset. The accuracy is evaluated under three conditions: clean rationales, irrelevant rationales, and inaccurate rationales. The table shows the average accuracy across different difficulty levels (Easy, Medium, Hard) for each task type (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense). The best and second-best results for each condition are highlighted in bold and underlined, respectively. The baseline model results (Base) are shown in gray for comparison. This table helps to understand the robustness of LLMs and reasoning methods in dealing with noisy rationales.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy of different language models and reasoning methods on the NoRa dataset. It shows the performance across three conditions: using clean rationales, irrelevant rationales, and inaccurate rationales. The results are broken down by task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense) and difficulty level (Easy, Medium, Hard). The best accuracy for each condition is highlighted in bold. The table helps to assess the robustness of different LLMs and methods when presented with noisy rationales.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy of several LLMs and reasoning methods on the NoRa dataset, categorized by task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense), method (Base, w/ ISC, w/ SP, w/ SM, w/ SD, w/ SC, w/SCO, w/BT, w/CC, w/ CD-CoT), and rationale type (clean, irrelevant, inaccurate). The accuracy is shown for ‘Easy’, ‘Medium’, and ‘Hard’ difficulty levels for each task. Bold numbers indicate the highest accuracy for a given task and rationale type, and underlined numbers show the second highest accuracy. The table highlights the significant drop in accuracy for LLMs when presented with irrelevant or inaccurate rationales compared to clean rationales.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the results of evaluating several language models and reasoning methods on the NoRa dataset. It shows the accuracy of each method on three different types of rationales (clean, irrelevant, and inaccurate) across three difficulty levels (easy, medium, hard) for three different reasoning tasks (Math Base-9, Math Base-11, Symbolic Equal). The gray rows highlight the baseline performance of the main LLM used in the study.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy results of several LLMs and reasoning methods on the NoRa dataset. It compares the performance on three different types of rationales: clean, irrelevant, and inaccurate. The table helps to understand the impact of noisy rationales on the accuracy of different LLMs and the effectiveness of existing robust methods. The results are shown for three difficulty levels (Easy, Medium, Hard) within each task type.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy of several LLMs and robust methods on the NoRa dataset, broken down by three types of rationales: clean, irrelevant, and inaccurate. It shows the performance of the base model (GPT-3.5-turbo) and five different baseline methods (ISC, SP, SM, SD, SC) across different difficulty levels (Easy, Medium, Hard) for three reasoning tasks (Math Base-9, Math Base-11, Symbolic Equal). The best and second-best results for each condition are highlighted.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy results of various LLMs and reasoning methods on the NoRa dataset. Different prompting example types are compared: clean, irrelevant, and inaccurate rationales. The table shows the accuracy for each method across different difficulty levels (easy, medium, hard) for each task type (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense). The best results for each task and difficulty are highlighted.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
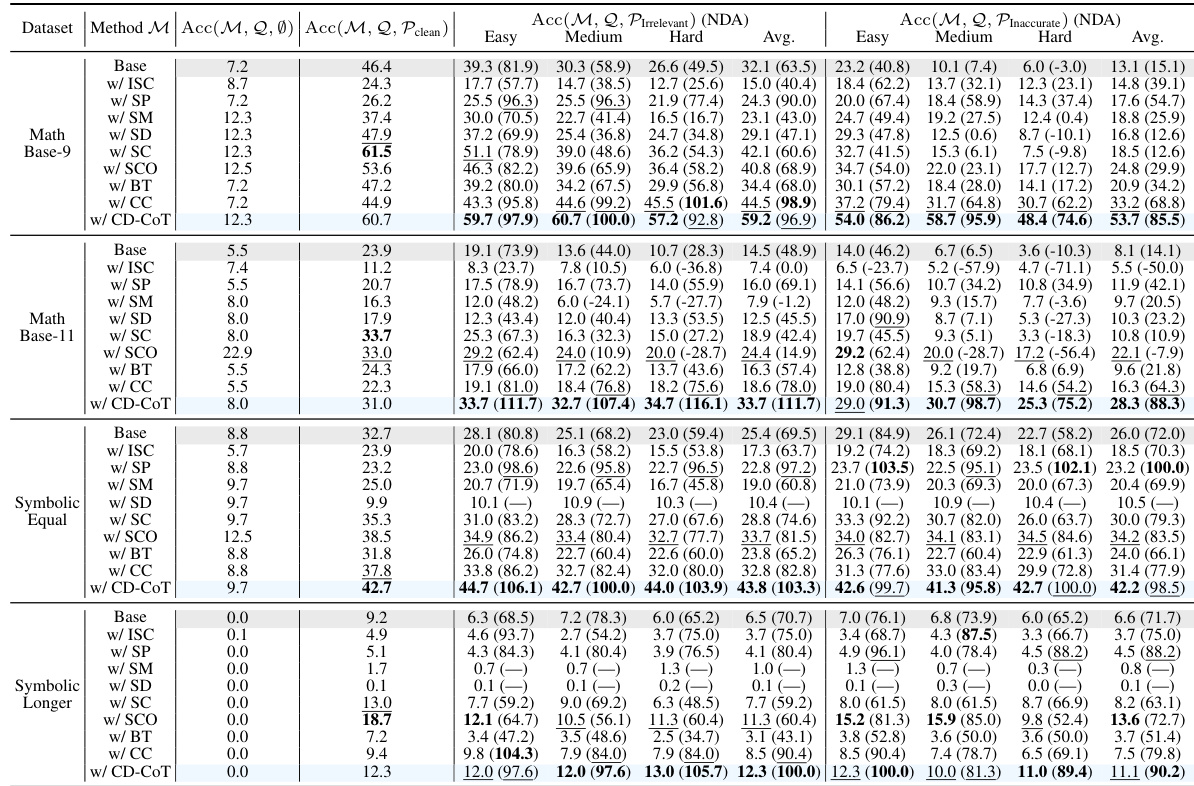
🔼 This table presents the accuracy results of different LLMs and robust methods on the NoRa dataset. It shows the accuracy of each method under three conditions: clean rationales, irrelevant rationales, and inaccurate rationales. The results are broken down by task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, and Commonsense) and difficulty level (Easy, Medium, Hard). The best performing method for each task and condition is highlighted in bold.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
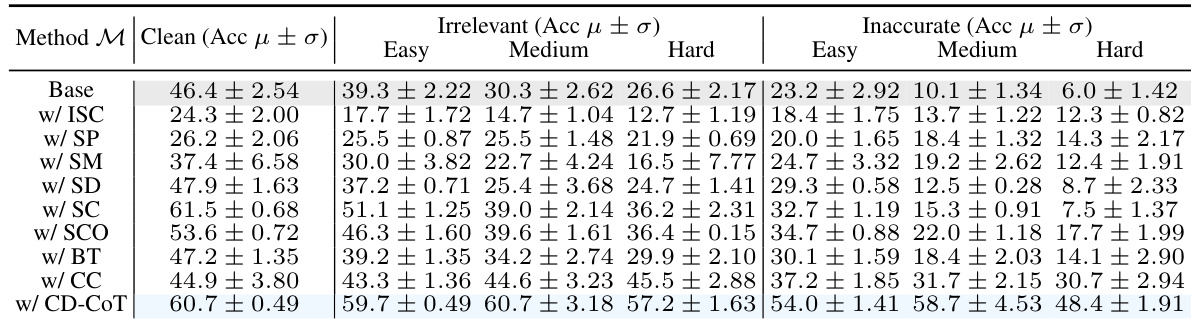
🔼 This table presents the results of evaluating several LLMs and robust methods on the NoRa dataset. It shows the accuracy of each model on three types of rationales (clean, irrelevant, and inaccurate) for three difficulty levels (easy, medium, hard) across three tasks. The bold numbers indicate the best performance for each scenario, and the underlined numbers indicate the second-best. The table highlights the significant performance drop of all models when using noisy rationales, demonstrating their vulnerability to noise. The gray highlights show the baseline performance of the Base model.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
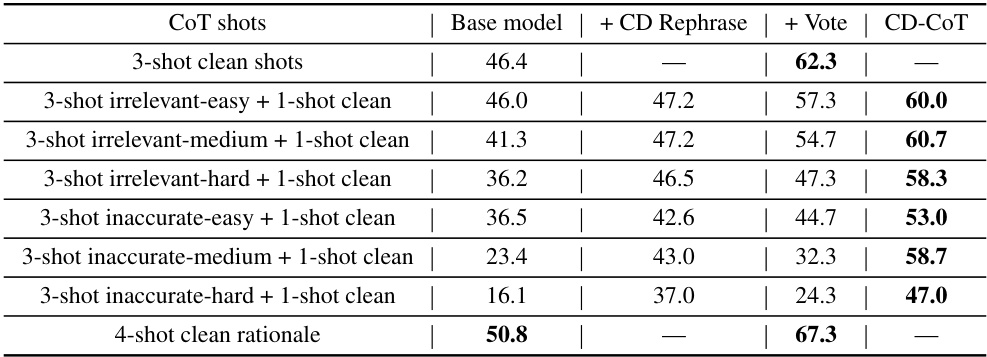
🔼 This table presents the accuracy of different language models and reasoning methods on the NoRa dataset. It shows the performance for each model under three conditions: clean rationales, irrelevant rationales, and inaccurate rationales. The results are broken down by difficulty level (easy, medium, hard) and task type (math, symbolic, commonsense). The best results are highlighted in bold, and the second-best are underlined. Base model results are shown in gray for comparison.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy of various LLMs and reasoning methods on the NoRa dataset when prompted with 3-shot examples. The results are categorized by task type (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense), rationale type (clean, irrelevant, inaccurate), and method (Base, w/ISC, w/SP, w/SM, w/SD, w/SC, w/SCO, w/BT, w/CC, w/CD-CoT). The boldface numbers indicate the best performance for each condition, while the underlined numbers indicate the second-best performance. The results for the Base model (without any additional methods) are highlighted in gray to facilitate comparison.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
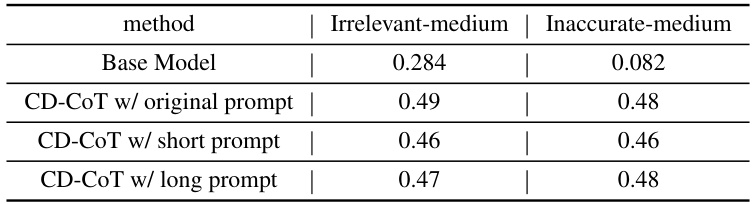
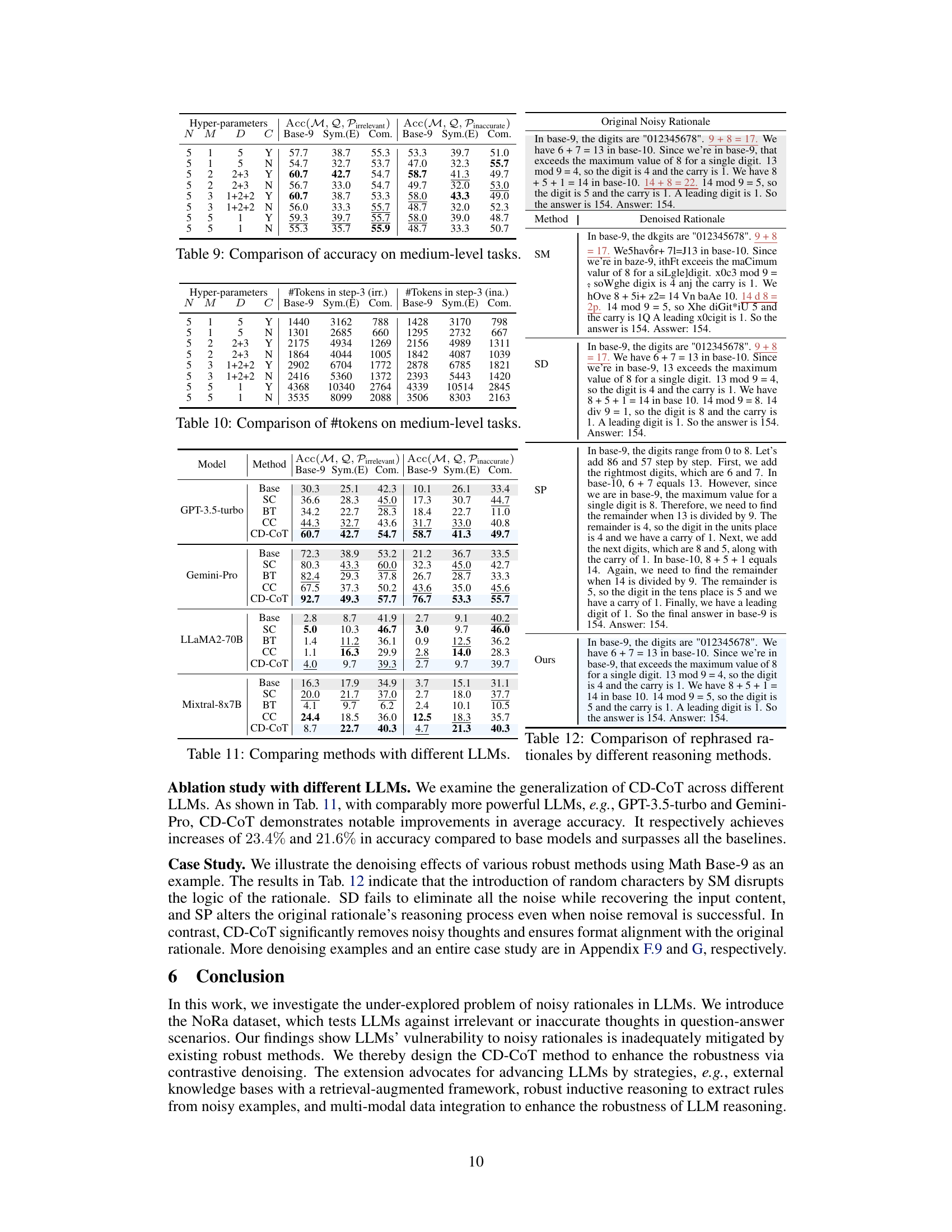
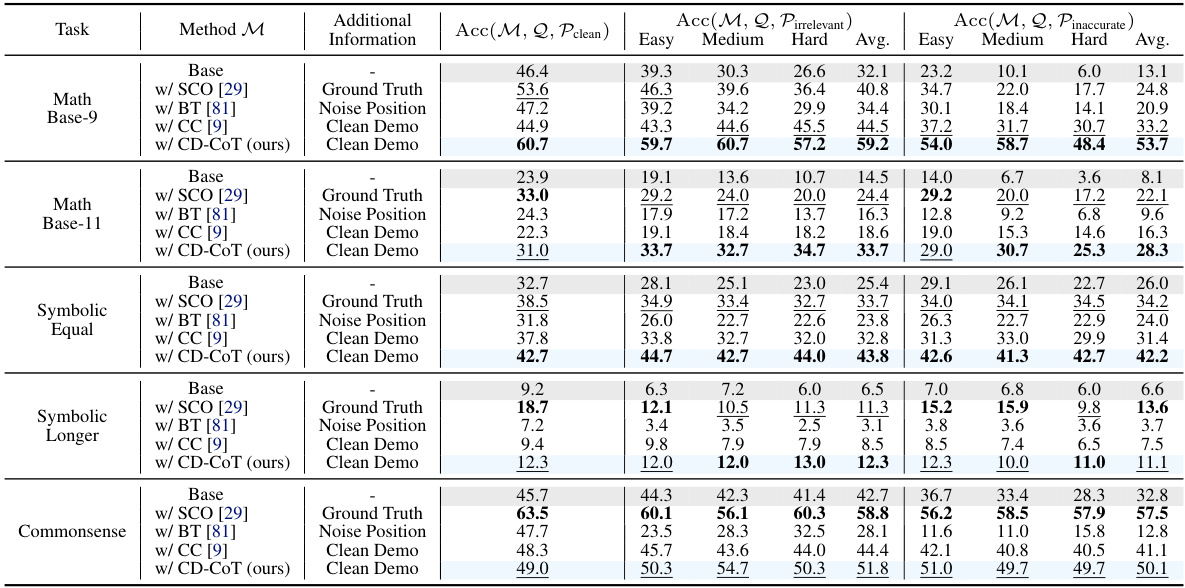
🔼 This table presents the results of an ablation study conducted to evaluate the impact of using different prompts on the performance of the CD-CoT method. Three different prompts were tested: the original prompt, a shorter prompt, and a longer prompt. The results show that the performance of CD-CoT is only marginally influenced by the choice of prompt. The table shows the NDA scores for both irrelevant and inaccurate medium-level noise.
read the caption
Table 35: Ablation study of different prompts in CD-CoT.
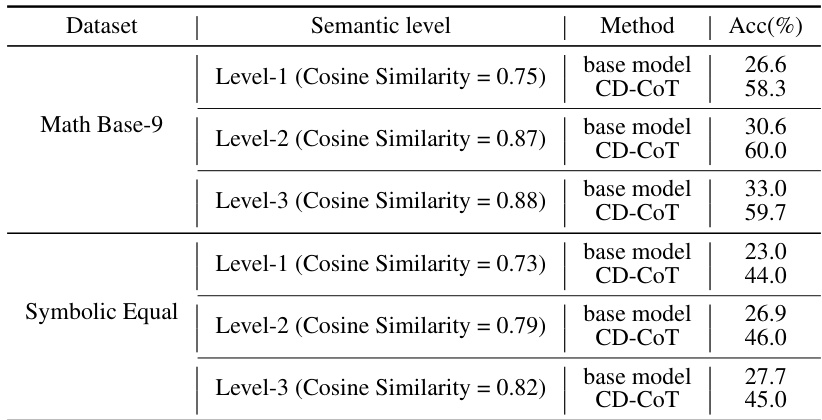
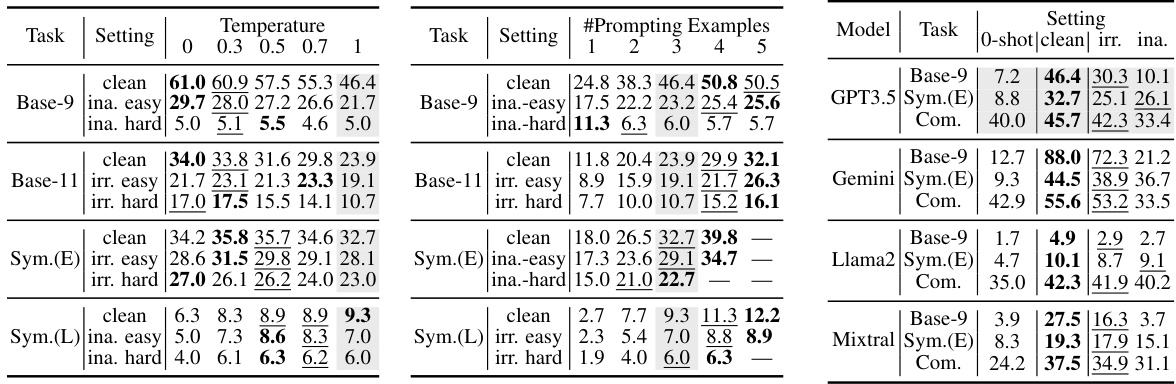
🔼 This table presents the accuracy results of several denoising methods on the NoRa dataset. It compares the performance of various methods across different reasoning tasks (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense) and difficulty levels (Easy, Medium, Hard). Each method’s performance is evaluated under three conditions: (1) clean rationales, (2) irrelevant rationales, and (3) inaccurate rationales. The table also shows the type of additional information required by each method, such as ground truth, noise position, or a clean demonstration. The aim is to compare the effectiveness of these methods in handling noisy rationales and highlight the advantages and disadvantages of each approach in terms of accuracy and the need for additional information.
read the caption
Table 8: Performance of denoising methods that require additional information for supervision.

🔼 This table presents the accuracy of different language models and reasoning methods on the NoRa dataset. It shows the accuracy for three types of rationales (clean, irrelevant, and inaccurate) across three difficulty levels (easy, medium, hard) for two mathematical tasks (Base-9, Base-11), and two symbolic tasks (Equal, Longer), and a commonsense task. The baseline model’s performance with clean rationales is presented for comparison. Bold numbers highlight the best performance among all methods for that task and rationale type, while underlined numbers show the second-best performance.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
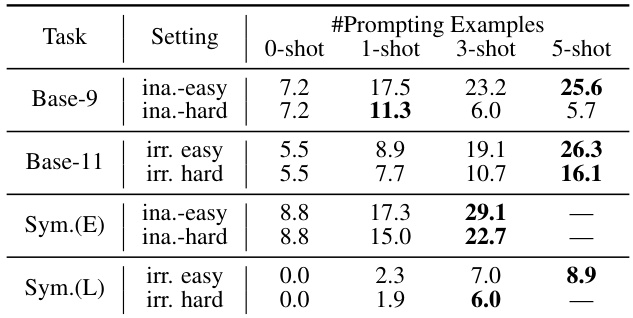
🔼 This table presents the accuracy results of different language models on the NoRa dataset under three different few-shot shuffle configurations: shuffling questions, shuffling rationales, and shuffling answers. The purpose is to investigate whether LLMs heavily rely on the exact mapping between questions, rationales, and answers in few-shot prompting scenarios. It is observed that shuffling the mappings degrades the reasoning performance but still performs better than without prompting. This suggests that LLMs may not rely heavily on the exact mapping but learn abstract information from demonstrations.
read the caption
Table 7: Performance (in accuracy%) on NoRa dataset under different few-shot shuffle configurations.

🔼 This table presents the breakdown of results from experiments comparing 0-shot, 1-shot, and 3-shot prompting scenarios, categorizing outcomes based on whether the model answered correctly (C) or wrongly (W) at each stage. It analyzes the transitions in model accuracy across different numbers of noisy examples.
read the caption
Table 41: Results partition of (0-shot, 1-shot, 3-shot).
🔼 This table presents the accuracy results of several LLMs and reasoning methods on the NoRa dataset. Three different types of rationales are used: clean, irrelevant, and inaccurate. The accuracy for each model and type of rationale is shown for three difficulty levels (Easy, Medium, Hard). The Base model’s accuracy for clean rationales is highlighted in gray to provide a clear benchmark for comparison. The best and second-best results are indicated in bold and underlined, respectively.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

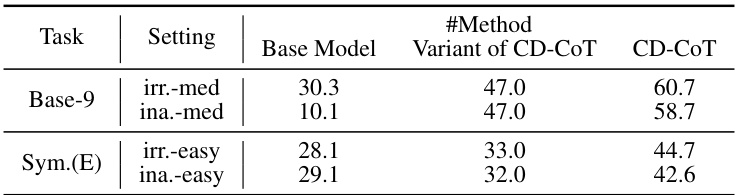
🔼 This table presents the accuracy of several denoising methods across different reasoning tasks and noise levels on the NoRa dataset. The methods include self-correction with oracle feedback (SCO), backtracking (BT), contrastive chain-of-thought (CC), and the proposed contrastive denoising with noisy chain-of-thought (CD-CoT). The table shows the performance (accuracy) for each method on tasks with clean rationales, irrelevant noise, and inaccurate noise. The ‘Additional Information’ column indicates the type of extra information each method needs. It highlights the relative performance improvements of the proposed CD-CoT method compared to other methods.
read the caption
Table 8: Performance of denoising methods that require additional information for supervision.

🔼 This table presents the accuracy results of various LLMs and robust methods on the NoRa dataset. It compares the performance of these models when using clean rationales, irrelevant rationales, and inaccurate rationales. The results are broken down by task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense) and difficulty level (Easy, Medium, Hard). The table highlights the best and second-best performing models for each condition and indicates the base model’s performance for comparison.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy results of different language models and reasoning methods on the NoRa dataset. It shows the performance of each model when prompted with clean rationales, irrelevant rationales, and inaccurate rationales. The table highlights the best-performing method for each condition and uses boldface and underlines to indicate the top two performers. The gray highlighting indicates baseline performance.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the results of evaluating several language models on the NoRa dataset, specifically focusing on their ability to perform robust reasoning when presented with noisy rationales (clean, irrelevant, inaccurate). The accuracy of each model is reported for three difficulty levels (Easy, Medium, Hard) across three reasoning tasks. The use of bold and underlined font helps highlight the best and second-best performing models. The gray highlighting draws attention to the base model’s performance for comparison.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy results of different language models and reasoning methods on the NoRa dataset, categorized by task (Math-Base9, Math-Base11, Symbolic-Equal, Symbolic-Longer, Commonsense), method used (Base, w/ ISC, w/ SP, w/ SM, w/ SD, w/ SC), and type of rationale (clean, irrelevant, inaccurate). The accuracy is given as a percentage for each task difficulty level (Easy, Medium, Hard). The best and second-best results are highlighted, and the Base model results are shaded gray for easy comparison.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.

🔼 This table presents the accuracy results of several LLMs and robust methods on the NoRa dataset, categorized by task (Math-Base9, Math-Base11, Symbolic-Equal, Symbolic-Longer, Commonsense), method, and type of rationale (clean, irrelevant, inaccurate). The accuracy is shown for easy, medium, and hard difficulty levels for each task and type of rationale, providing a comprehensive evaluation of LLM robustness against noisy rationales. Boldface numbers indicate the best performance for each category, while underlined numbers show the second-best.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
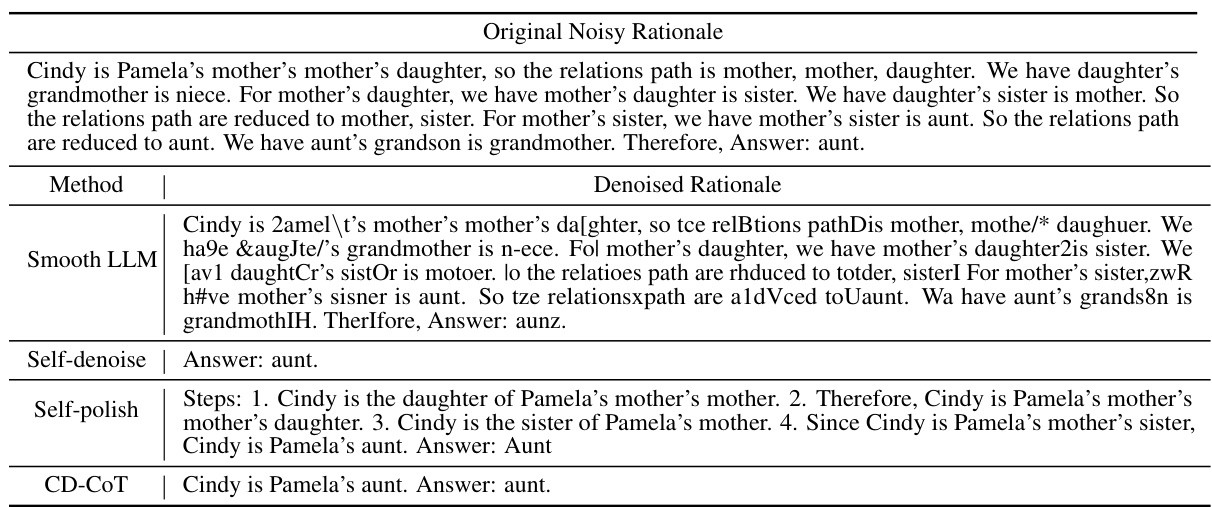
🔼 This table presents the accuracy of different language models and reasoning methods on the NoRa dataset when using 3-shot prompting examples with different types of rationales: clean, irrelevant, and inaccurate. The results are categorized by task (Math Base-9, Math Base-11, Symbolic Equal, Symbolic Longer, Commonsense) and difficulty level (Easy, Medium, Hard). The table highlights the best performing model for each scenario and indicates the second-best results. It also shows a comparison to a base model’s performance. The gray highlights indicate the base model’s results.
read the caption
Table 3: Reasoning accuracy on NoRa dataset with 3-shot prompting examples with clean, irrelevant, or inaccurate rationales. The boldface numbers mean the best results, while the underlines numbers indicate the second-best results. Note the referenced results of Base model are highlighted in gray.
Full paper#