TL;DR#
Diffusion models are powerful generative models but often struggle with slow sampling. Diffusion bridge models, designed for coupled data distributions (e.g., image-to-image translation), further exacerbate this issue due to their complex sampling process. The high computational cost hinders their practical applications. This research introduces Consistency Diffusion Bridge Models (CDBMs) to tackle this problem.
The core of CDBMs lies in learning the consistency function of the probability flow ordinary differential equation (PF-ODE) within diffusion bridges. This allows for direct prediction of the solution at a starting step, significantly reducing the number of network evaluations required during sampling. Two training paradigms (consistency bridge distillation and consistency bridge training) are proposed, enhancing the flexibility of CDBMs across different model designs. Experiments demonstrate that CDBMs achieve a 4x to 50x speedup compared to baseline diffusion bridge models, while maintaining or even improving visual quality.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on generative models and especially diffusion models. It presents significant advancements in sampling efficiency, a major bottleneck in the practical application of these models. The proposed method offers a faster and more efficient approach with improved visual quality, opening new avenues for various downstream tasks and applications. The unified framework is particularly valuable for broader adoption and further research.
Visual Insights#
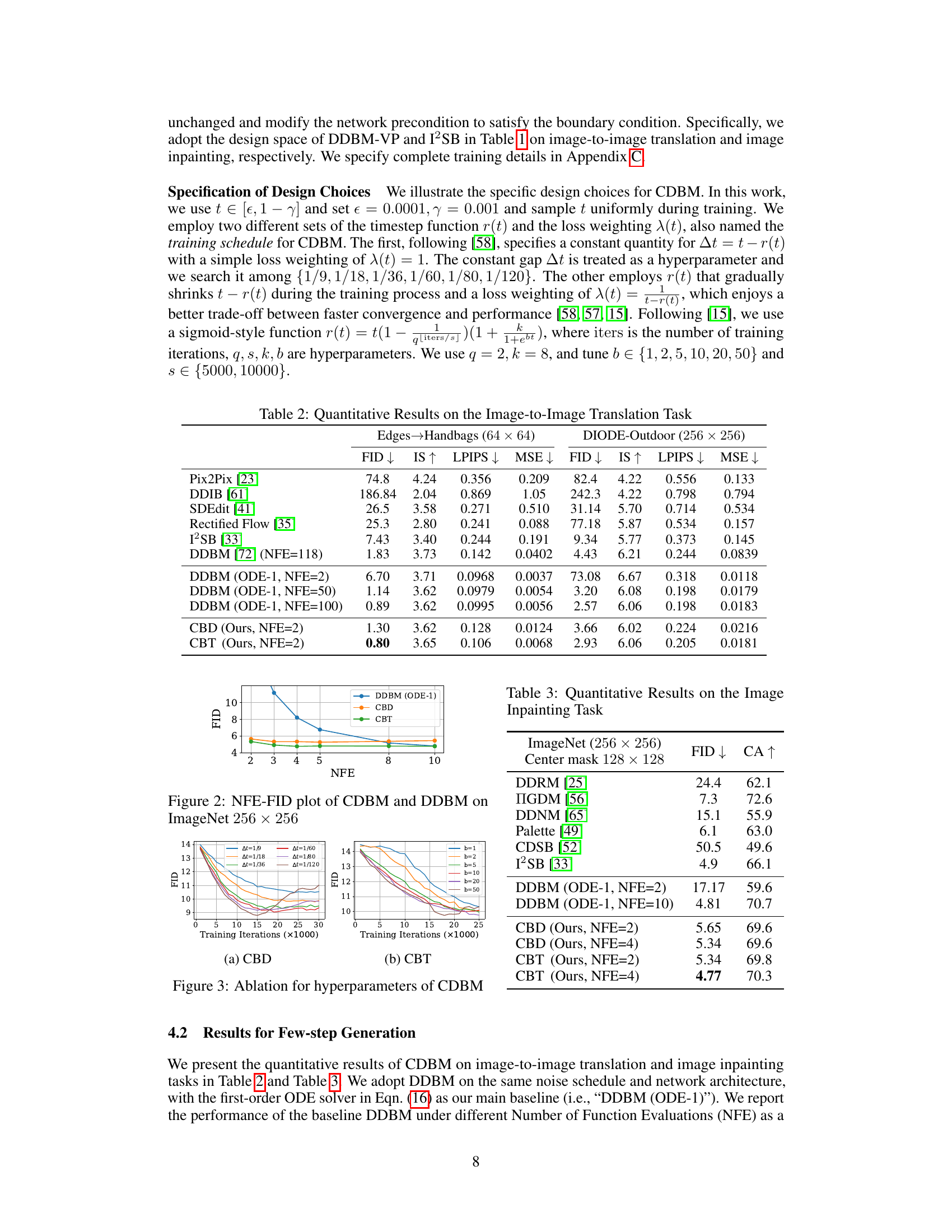
🔼 This figure illustrates the core idea of the proposed Consistency Diffusion Bridge Models (CDBMs). It compares the traditional diffusion models’ probability flow ordinary differential equation (PF-ODE) with the PF-ODE of diffusion bridges. The key difference is that diffusion bridges have fixed endpoints (start and end data points), unlike diffusion models which start from pure noise. Because of this singularity at the end point, the diffusion bridge PF-ODE is only well-defined before the end time, T. The figure shows how CDBMs use this PF-ODE, requiring an initial step (one-step posterior sampling) to get a point before the singularity, and then using a consistency function to predict the final result directly.
read the caption
Figure 1: Illustration of consistency models (CMs) on PF-ODEs of diffusion models and our proposed consistency diffusion bridge models (CDBMs) building on PF-ODEs of diffusion bridges. Different from diffusion models, the PF-ODE of diffusion bridge is only well defined in t < T due to the singularity induced by the fixed terminal endpoint. To this end, a valid input for CDBMs is some xt for t

🔼 This table compares the design spaces of four different diffusion bridge models: Brownian Bridge, I2SB, DDBM, and Bridge-TTS. It details the noise schedule parameters (T, f(t), g²(t), αt, σt, ρt, etc.) for each model, highlighting their differences in how these parameters are defined and calculated. It also shows the parameterization used by the neural network Fθ to predict the data, illustrating the design choices for each model.
read the caption
Table 1: Specifications of design spaces in different diffusion bridges. The details of network parameterization are in Appendix B.4 due to space limit.
In-depth insights#
Bridge ODE Solver#
The concept of a ‘Bridge ODE Solver’ within the context of diffusion models is crucial for efficient sampling. It represents a specialized numerical method designed to solve the ordinary differential equation (ODE) that governs the reverse-time diffusion process in diffusion bridge models. Unlike standard ODE solvers, a Bridge ODE solver must handle the boundary conditions inherent to diffusion bridges, where the process is constrained to start and end at specific points. This necessitates an algorithm robust to potential singularities or numerical instability that might arise near the boundary. The efficiency and accuracy of such a solver are critical since repeated ODE solves are necessary during sampling, making a highly efficient and precise Bridge ODE solver paramount for the practical application of this advanced generative modeling technique. The choice of solver directly influences sampling speed and sample quality, highlighting the importance of designing or selecting an algorithm well-suited to the mathematical characteristics of bridge ODEs.
Consistency Models#
Consistency models, a significant advancement in diffusion models, address the slow sampling speed inherent in traditional approaches. They achieve this by learning a consistency function that directly predicts the solution of a probability-flow ordinary differential equation (PF-ODE) at a target timestep, bypassing the iterative denoising process. This one-step generation drastically reduces computational cost, improving sampling efficiency by orders of magnitude. The core idea is to predict the final denoised image directly from a noisy input, eliminating the need for multiple network evaluations. While initially developed for standard diffusion models, their application to diffusion bridge models offers exciting potential for improved performance in tasks involving coupled data distributions. Consistency models offer a powerful alternative to traditional diffusion model sampling, promising faster generation times and potentially better image quality with the same computational resources.
DDBM Efficiency#
The efficiency of Denoising Diffusion Bridge Models (DDBMs) is a critical factor determining their practical applicability. DDBMs, while powerful for tasks involving coupled data distributions, suffer from the computational burden of their sampling process, often requiring hundreds of network evaluations for decent sample quality. This high computational cost significantly hinders their deployment in resource-constrained environments or real-time applications. Therefore, improving DDBM efficiency is paramount. The core challenge lies in accelerating the sampling process while maintaining or improving the quality of generated samples. Strategies to address this efficiency bottleneck often center on developing faster sampling algorithms or approximating the underlying stochastic process more efficiently. Approaches leveraging consistency models, as explored in the provided paper, offer a promising path towards this goal by directly learning a consistency function that can predict the solution of the probability flow ordinary differential equation, thereby drastically reducing the number of network evaluations required for sampling.
Unified Design#
A unified design in the context of a research paper, likely focusing on machine learning or a related field, suggests a standardization or harmonization of different approaches, models, or techniques. This would aim to create a more consistent and streamlined workflow, making it easier to compare results, reproduce experiments, and improve the overall efficiency of the research process. A key benefit is improved modularity, allowing components from various methods to be combined more easily. This often involves defining a common interface or framework that simplifies the interaction between different parts of a system. Such a framework could simplify the process of experimentation and model development. However, achieving a truly unified design can be challenging, requiring careful consideration of trade-offs and potentially some loss of specialized functionality found in more niche or specialized approaches. The success of a unified design often depends on the acceptance and adoption within the research community, which could be limited by existing workflows, the diversity of different approaches, and a lack of standardized formats. Therefore, a unified design represents a significant step toward improved collaboration and efficiency in research, but its practicality and acceptance are dependent on community buy-in and the inherent complexities of the problem domain.
Future Work#
The ‘Future Work’ section of a research paper on consistency diffusion bridge models could explore several promising avenues. Extending the framework to handle more complex data modalities beyond images, such as video or 3D point clouds, would be a significant step. Investigating the theoretical properties of CDBMs more rigorously is crucial, especially concerning their stability and convergence. Addressing the numerical instability inherent in consistency models is also important, potentially through improved ODE solvers or alternative optimization techniques. Exploring the use of different neural network architectures and noise schedules is also warranted to investigate the generalizability of the approach. Finally, a thorough evaluation on a wider range of downstream tasks, beyond image translation and inpainting, such as image generation and editing, is needed to confirm its effectiveness and versatility. Investigating connections to other generative models would be beneficial, potentially leading to novel hybrid approaches. In addition, a detailed investigation into the ethical implications of improved efficiency in generating high-quality synthetic media should be included.
More visual insights#
More on figures
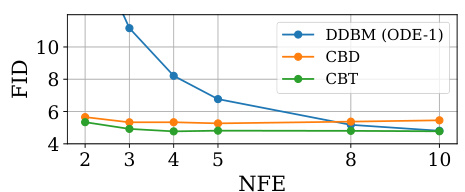
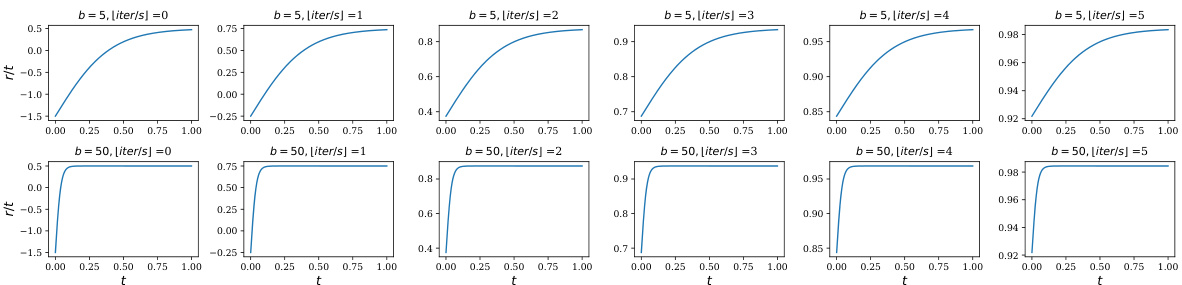
🔼 This figure shows the ablation study for the hyperparameters of CDBM (Consistency Diffusion Bridge Models) on the ImageNet dataset. The ablation study focuses on the impact of different settings for the hyperparameters on model performance. Specifically, it examines the effect of two sets of timestep functions, r(t), and loss weighting functions, λ(t), which govern the training schedule of the CDBM. The first uses a constant timestep interval (∆t) and a constant loss weighting of 1, while the second employs a variable timestep interval that gradually shrinks during training and a loss weighting of tλ(t). The results are visualized as FID (Fréchet Inception Distance) plots against training iterations for different hyperparameter choices. The figure helps in determining the optimal combination of hyperparameters for better performance in CDBM.
read the caption
Figure 3: Ablation for hyperparameters of CDBM
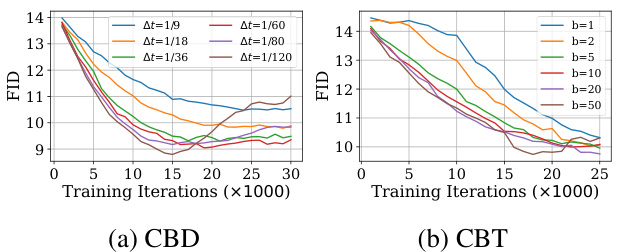
🔼 This figure shows the ablation study for the hyperparameters of CDBM on ImageNet 256x256. It presents two subfigures, one for CBD (consistency bridge distillation) and one for CBT (consistency bridge training). Each subfigure displays FID (Fréchet Inception Distance) curves across different training iterations for various hyperparameter settings. The CBD subfigure demonstrates the impact of different constant time step intervals (Δt) on the training process. The CBT subfigure showcases the effect of different values of the hyperparameter ‘b’ in a sigmoid-style training schedule on training performance. The results help to determine the optimal hyperparameter settings for better performance in the training of CDBM.
read the caption
Figure 3: Ablation for hyperparameters of CDBM

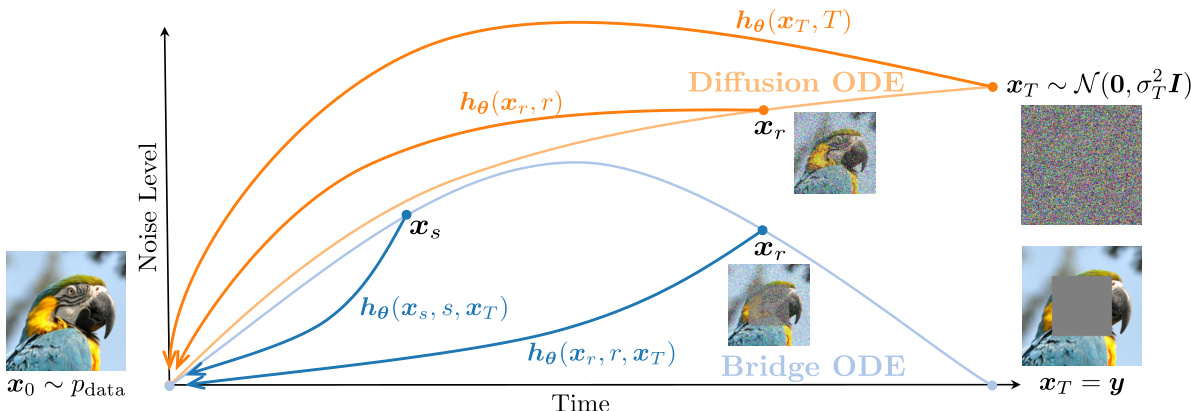
🔼 This figure demonstrates the qualitative comparison of image generation results between the baseline DDBM (Denoising Diffusion Bridge Models) and the proposed CDBM (Consistency Diffusion Bridge Models) across three different tasks: image-to-image translation (Edges to Handbags), image-to-image translation (DIODE-Outdoor), and image inpainting (ImageNet). It visually shows the improved sample quality and reduced blurring artifacts achieved by CDBM with significantly fewer function evaluations (NFEs).
read the caption
Figure 4: Qualitative demonstration between DDBM and CDBM.

🔼 This figure shows an example of semantic interpolation using CDBMs. Semantic interpolation is a technique that allows for the generation of intermediate samples between two given samples, representing a smooth transition in the semantic space. The figure visually demonstrates this capability by showing a sequence of images that smoothly transition between two distinct input images. This highlights the ability of CDBMs to not only generate samples but also to manipulate and control the semantic content of those samples.
read the caption
Figure 5: Example semantic interpolation result with CDBMs.
🔼 This figure illustrates the core idea of the proposed Consistency Diffusion Bridge Models (CDBMs). It compares the probability flow ordinary differential equations (PF-ODEs) of standard diffusion models and diffusion bridge models. The key difference is that diffusion bridges have fixed endpoints, leading to a singularity at the end of the process (time T). CDBMs address this by learning a consistency function that directly predicts the solution at a starting step (t<T), overcoming the singularity issue and thus enabling more efficient sampling. A single step posterior sampling is used to obtain a starting point for CDBMs.
read the caption
Figure 1: Illustration of consistency models (CMs) on PF-ODEs of diffusion models and our proposed consistency diffusion bridge models (CDBMs) building on PF-ODEs of diffusion bridges. Different from diffusion models, the PF-ODE of diffusion bridge is only well defined in t < T due to the singularity induced by the fixed terminal endpoint. To this end, a valid input for CDBMs is some xt for t

🔼 This figure presents a qualitative comparison of image generation results between the baseline DDBM model and the proposed CDBM model. It visually demonstrates the improved sample quality achieved by CDBM, particularly in reducing blurring artifacts, even when using significantly fewer network function evaluations (NFEs). The figure showcases several image-to-image translation examples across different conditions and resolutions, highlighting the visual advantages of CDBM.
read the caption
Figure 4: Qualitative demonstration between DDBM and CDBM.

🔼 This figure presents a qualitative comparison of image generation results between the baseline DDBM (Denoising Diffusion Bridge Model) and the proposed CDBM (Consistency Diffusion Bridge Model) for image-to-image translation and image inpainting tasks. It visually showcases the improved sample quality and reduced artifacts achieved by CDBM, particularly when using a limited number of function evaluations (NFEs). The figure demonstrates that CDBM produces visually superior samples with the same or fewer function evaluations compared to DDBM.
read the caption
Figure 4: Qualitative demonstration between DDBM and CDBM.

🔼 This figure qualitatively compares the image generation results of DDBM and CDBM on different image-to-image translation and image inpainting tasks. It showcases that CDBM achieves better visual quality with fewer function evaluations than DDBM.
read the caption
Figure 4: Qualitative demonstration between DDBM and CDBM.

🔼 The figure illustrates the core idea of the paper: applying consistency models to diffusion bridge models. It shows how a consistency model directly predicts the solution of a probability flow ordinary differential equation (PF-ODE) at a certain starting timestep given any points in the ODE trajectory, improving the sampling efficiency of diffusion bridges. The figure also highlights the difference between the PF-ODEs of diffusion models and diffusion bridges, emphasizing that the PF-ODE of diffusion bridges is only well defined for t < T due to the singularity at T, which affects the input of consistency models.
read the caption
Figure 1: Illustration of consistency models (CMs) on PF-ODEs of diffusion models and our proposed consistency diffusion bridge models (CDBMs) building on PF-ODEs of diffusion bridges. Different from diffusion models, the PF-ODE of diffusion bridge is only well defined in t < T due to the singularity induced by the fixed terminal endpoint. To this end, a valid input for CDBMs is some xt for t < T, which is typically obtained by one-step posterior sampling with a coarse estimation of x with an initial network evaluation.

🔼 This figure shows a qualitative comparison of image generation results between the baseline DDBM model and the proposed CDBM model. It visually demonstrates that CDBM produces higher-quality images with less blurring, especially when using fewer function evaluations (NFEs). The improvement in visual quality highlights the effectiveness of CDBM in enhancing the sampling efficiency and image generation quality of diffusion bridge models.
read the caption
Figure 4: Qualitative demonstration between DDBM and CDBM.

🔼 This figure presents a qualitative comparison of the image generation results between the baseline DDBM (Denoising Diffusion Bridge Models) and the proposed CDBM (Consistency Diffusion Bridge Models) methods. It visually showcases the improved image quality and reduced artifacts achieved by CDBM, particularly noticeable in finer details and sharper results, when compared to DDBM with the same number of function evaluations (NFEs). The images across multiple image translation and inpainting tasks demonstrate the effectiveness of the proposed CDBM approach.
read the caption
Figure 4: Qualitative demonstration between DDBM and CDBM.

🔼 This figure illustrates the difference between consistency models applied to diffusion models and consistency diffusion bridge models. It highlights that the probability flow ordinary differential equation (PF-ODE) of diffusion bridges is only well-defined before the terminal time T, due to a singularity at the endpoint. This necessitates a different approach for CDBMs, using one-step posterior sampling to obtain a valid input before applying the consistency function.
read the caption
Figure 1: Illustration of consistency models (CMs) on PF-ODEs of diffusion models and our proposed consistency diffusion bridge models (CDBMs) building on PF-ODEs of diffusion bridges. Different from diffusion models, the PF-ODE of diffusion bridge is only well defined in t < T due to the singularity induced by the fixed terminal endpoint. To this end, a valid input for CDBMs is some xt for t < T, which is typically obtained by one-step posterior sampling with a coarse estimation of xT with an initial network evaluation.

🔼 This figure shows a qualitative comparison of the image generation results between DDBM and CDBM on three different image-to-image translation tasks. The results demonstrate that CDBM produces comparable or better image quality than DDBM using significantly fewer network function evaluations (NFEs). This highlights CDBM’s improved sampling efficiency.
read the caption
Figure 4: Qualitative demonstration between DDBM and CDBM.

🔼 This figure illustrates the core idea of the paper: using consistency models to speed up the sampling process of diffusion bridge models. It shows how consistency models predict the solution of the probability flow ordinary differential equation (PF-ODE) directly, avoiding the iterative process of standard diffusion models. The figure highlights the difference in the PF-ODE for diffusion models versus diffusion bridge models, emphasizing the singularity issue in the latter and how the proposed method addresses this.
read the caption
Figure 1: Illustration of consistency models (CMs) on PF-ODEs of diffusion models and our proposed consistency diffusion bridge models (CDBMs) building on PF-ODEs of diffusion bridges. Different from diffusion models, the PF-ODE of diffusion bridge is only well defined in t < T due to the singularity induced by the fixed terminal endpoint. To this end, a valid input for CDBMs is some xt for t < T, which is typically obtained by one-step posterior sampling with a coarse estimation of xT with an initial network evaluation.

🔼 This figure demonstrates the diversity of samples generated by the deterministic ODE sampler when starting from different points in the distribution qT-γ(xT-γ|xT~qT(xT|x0,xT=y)). It showcases that despite the deterministic nature of the ODE solver, variations in the starting point lead to a range of different plausible output images.
read the caption
Figure 10: Demonstration of sample diversity of the deterministic ODE sampler.

🔼 This figure compares the image inpainting results of CDBM and I2SB on ImageNet dataset (256x256 resolution) for the same condition. It shows that CDBM achieves comparable or better quality inpainting compared to I2SB using significantly fewer function evaluations (NFEs). Note that the CDBM model used here differs from the publicly available I2SB checkpoint.
read the caption
Figure 11: Qualitative comparison between CDBM and I2SB baseline on ImageNet 256 × 256. Note that here the base model of CDBM is different from the officially released checkpoint of I2SB we used for evaluation.
More on tables
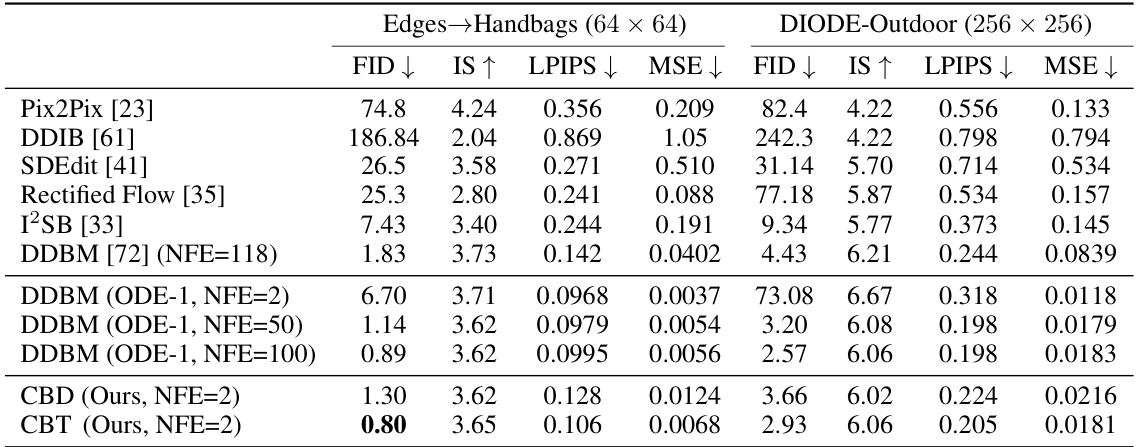
🔼 This table presents a quantitative comparison of different models on two image-to-image translation tasks: Edges→Handbags (64x64 resolution) and DIODE-Outdoor (256x256 resolution). The metrics used for comparison include FID (Fréchet Inception Distance), IS (Inception Score), LPIPS (Learned Perceptual Image Patch Similarity), and MSE (Mean Squared Error). The table shows the performance of various models, including baselines (Pix2Pix, DDIB, SDEdit, Rectified Flow, I2SB, and DDBM), as well as the proposed CDBM models (CBD and CBT) with different numbers of function evaluations (NFE). Lower FID and LPIPS values, and higher IS values indicate better performance.
read the caption
Table 2: Quantitative Results on the Image-to-Image Translation Task
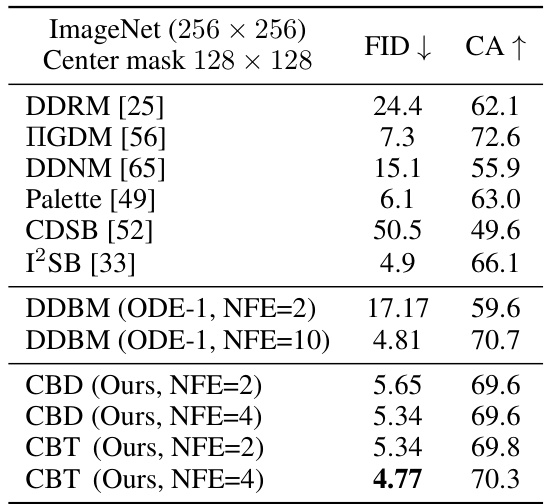
🔼 This table presents a quantitative comparison of different image inpainting methods on the ImageNet dataset. The metrics used are FID (Fréchet Inception Distance), a measure of the visual quality and diversity of generated images; and CA (Classifier Accuracy), which assesses how well the inpainted images are classified compared to ground truth images using a pre-trained ResNet50 classifier. The results show the FID and CA scores for various methods, including the proposed CDBM (Consistency Diffusion Bridge Model) at different number of function evaluations (NFE). Lower FID scores indicate higher image quality, while higher CA scores show better image classification accuracy.
read the caption
Table 3: Quantitative Results on the Image Inpainting Task

🔼 This table compares the design choices for various diffusion bridge models, including noise schedule, prediction target, network parameterization, and precondition. It highlights the unified design space proposed in the paper, which allows for flexible integration of consistency models into DDBMs. Note that the details of the network parameterization are deferred to Appendix B.4 due to space limitations in the main paper.
read the caption
Table 1: Specifications of design spaces in different diffusion bridges. The details of network parameterization are in Appendix B.4 due to space limit.
Full paper#