TL;DR#
Vision Transformers (ViTs) have achieved remarkable success in computer vision, but their theoretical understanding, especially regarding generalization when overfitting, remains limited. This paper addresses this gap by focusing on the phenomenon of benign overfitting, where models generalize well despite perfectly memorizing the training data. Prior research on the optimization and generalization of ViTs often employs simplified settings, hindering a comprehensive understanding of their complex behavior.
To overcome these limitations, the study uses a simplified two-layer ViT model with softmax attention and a novel theoretical framework based on feature learning theory. By carefully analyzing the training dynamics in three distinct phases, they characterize the optimization process and establish a sharp condition (dependent on the data’s signal-to-noise ratio) that distinguishes benign from harmful overfitting. The theoretical findings are verified through experimental simulation, offering crucial insights into ViTs’ behavior and highlighting the importance of the signal-to-noise ratio in ensuring successful generalization.
Key Takeaways#
Why does it matter?#
This paper is crucial because it’s the first to theoretically characterize benign overfitting in Vision Transformers (ViTs), a phenomenon where models generalize well despite memorizing training data. This deepens our understanding of ViTs’ generalization capabilities and offers valuable insights for improving their performance and robustness. The sharp conditions established can guide future research in designing more effective ViTs.
Visual Insights#

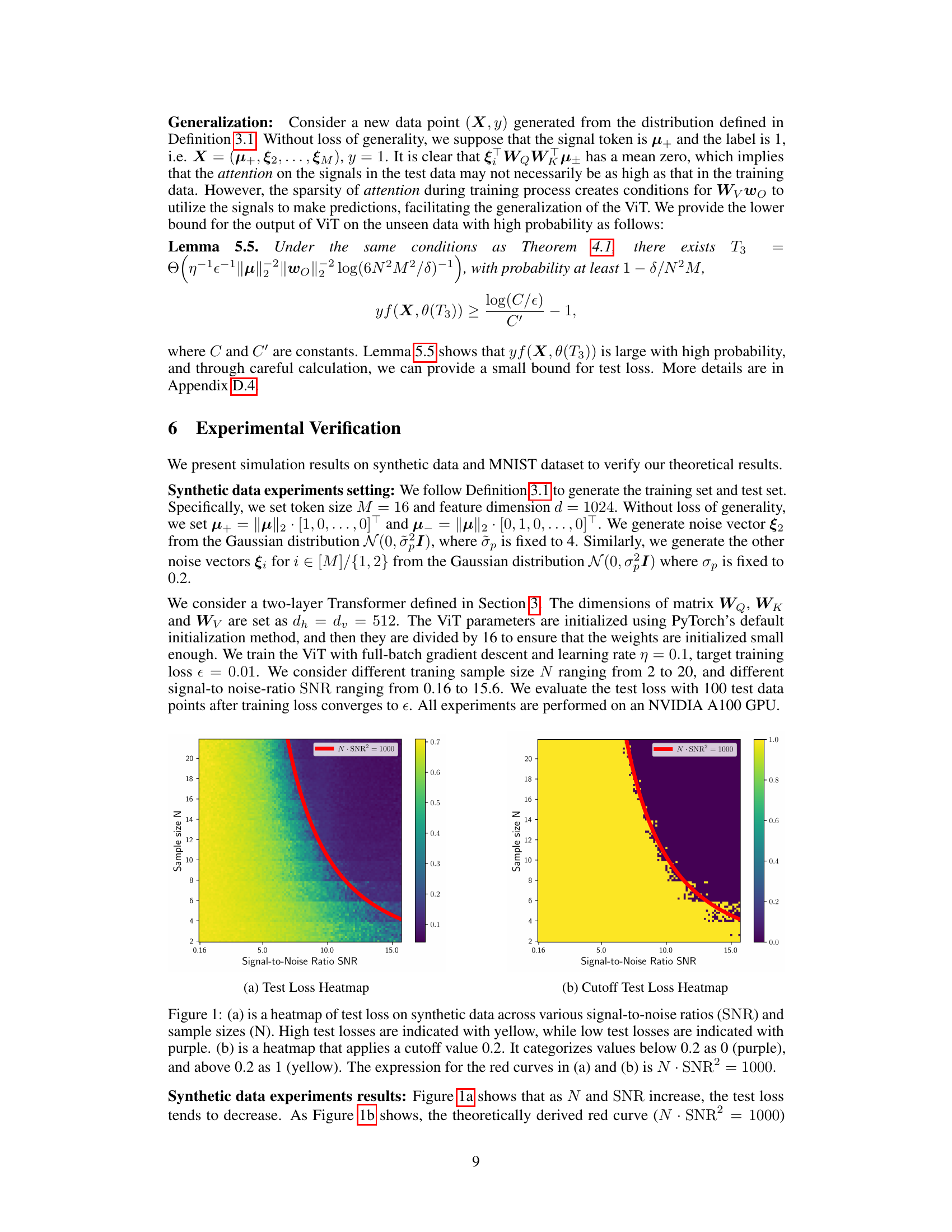
🔼 This figure shows the test loss results from experiments on synthetic data with varying sample sizes (N) and signal-to-noise ratios (SNR). The heatmaps visualize the relationship between these parameters and test loss. A cutoff at a test loss of 0.2 helps to highlight the transition between benign and harmful overfitting regimes; the red curve represents the theoretical boundary N*SNR^2 = 1000 separating the two regimes.
read the caption
Figure 1: (a) is a heatmap of test loss on synthetic data across various signal-to-noise ratios (SNR) and sample sizes (N). High test losses are indicated with yellow, while low test losses are indicated with purple. (b) is a heatmap that applies a cutoff value 0.2. It categorizes values below 0.2 as 0 (purple), and above 0.2 as 1 (yellow). The expression for the red curves in (a) and (b) is N · SNR² = 1000.

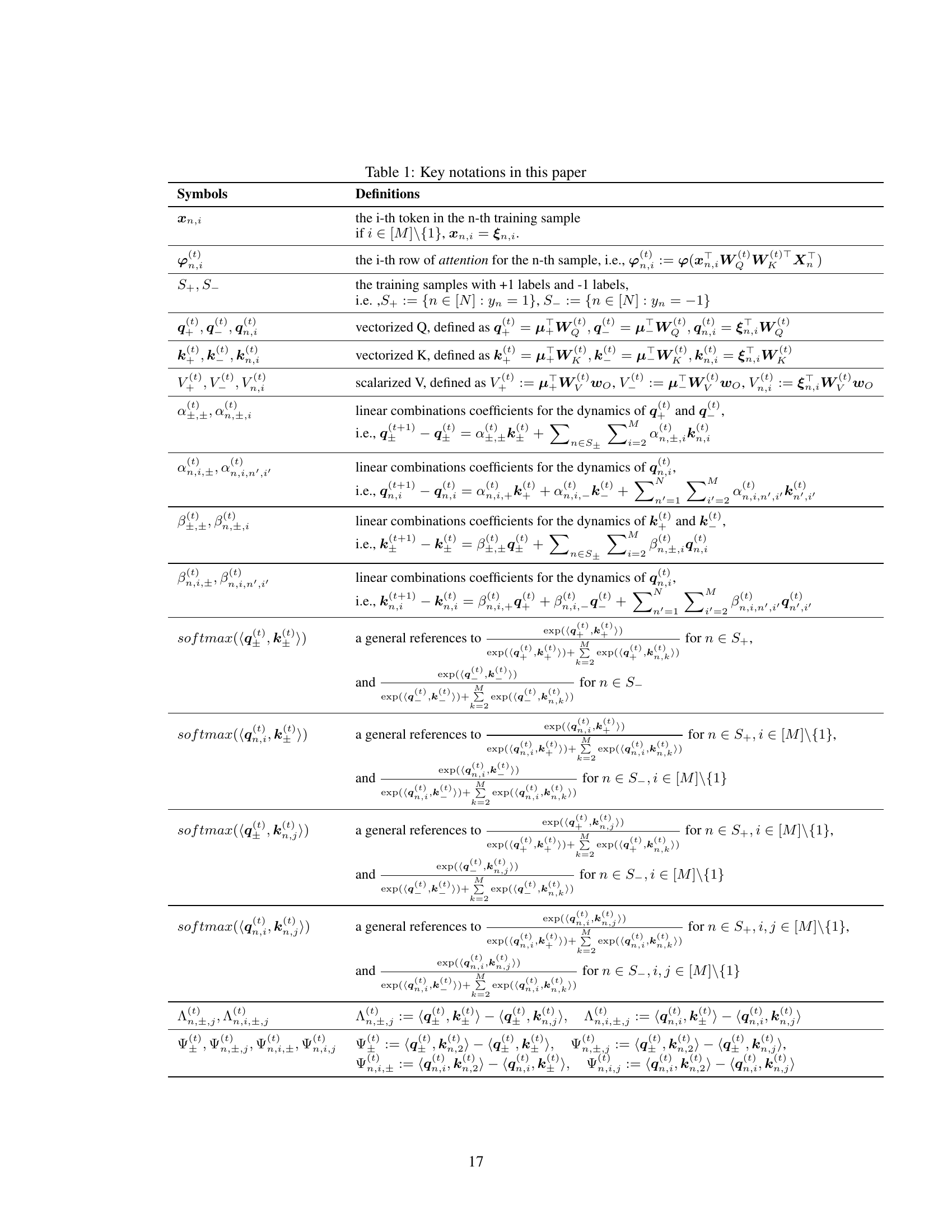
🔼 This table lists key notations used in the paper. It defines symbols for various components of the Vision Transformer model (tokens, attention matrices, vectorized representations, etc.) and describes the mathematical notations used to analyze the model’s training dynamics and optimization.
read the caption
Table 1: Key notations in this paper
In-depth insights#
ViT Overfitting#
Vision Transformers (ViTs) have shown remarkable success in various computer vision tasks. However, their susceptibility to overfitting, especially when trained on limited datasets, remains a significant concern. Understanding the dynamics of ViT overfitting is crucial for improving generalization and robustness. This involves analyzing how the model’s parameters adapt during training, leading to memorization of training data rather than learning generalizable features. Investigating different regularization techniques, architectural modifications, and data augmentation strategies to mitigate overfitting in ViTs is essential. Furthermore, theoretical analysis is needed to provide a comprehensive understanding of ViT overfitting, identifying factors contributing to it and establishing conditions for benign versus harmful overfitting. Research into benign overfitting scenarios is key, where overfitting does not impair generalization performance. This requires exploring different aspects of the training process, such as optimization algorithms, loss functions, and data distributions. The ultimate goal is to develop strategies that enable ViTs to achieve optimal performance on unseen data while minimizing the risks associated with overfitting.
Training Dynamics#
The study of “Training Dynamics” in the context of Vision Transformers (ViTs) reveals crucial insights into their optimization and generalization capabilities. The paper characterizes three distinct phases in the training process. These phases demonstrate unique optimization behaviors linked to the self-attention mechanism. The initial phase focuses on signal extraction, while the latter phase is characterized by the model’s response to both signals and noise. The model’s ability to generalize, a phenomenon known as benign overfitting, is studied in-depth. A sharp separation condition is established, separating the regimes of benign and harmful overfitting based on the signal-to-noise ratio in the data. The theoretical analysis is verified by experimental simulations, which show a sharp transition between the two regimes, reinforcing the importance of the signal-to-noise ratio in determining the model’s generalization performance. The novel methodology employed overcomes challenges posed by the non-linearity of the softmax function and the interdependent nature of transformer weights, allowing for a detailed theoretical analysis of a complex architecture and providing valuable guidance for training ViTs effectively.
Sharp Condition#
The concept of a “Sharp Condition” in a research paper usually refers to a precisely defined boundary or threshold that distinguishes between two significantly different behaviors or regimes. In the context of a machine learning study, a sharp condition might delineate the boundary between successful generalization (benign overfitting) and poor generalization (harmful overfitting) for a model. The sharpness implies a lack of ambiguity in the condition. A small change in the parameters or data characteristics that satisfy the condition could lead to a drastically different outcome. This makes the condition particularly interesting for theoretical analysis. It implies a fundamental shift in the model’s behavior as the condition is crossed. A sharp condition would be contrasted with a gradual or fuzzy transition where a shift in behavior occurs over a range of values rather than at a single point. For example, a sharp condition could involve a specific signal-to-noise ratio, model size, or data distribution parameter, where even small deviations from that point will cause the model’s performance to change substantially. In a research paper, establishing a sharp condition is a strong theoretical contribution as it provides clear-cut criteria to understand the system and its behavior rather than simply stating trends or qualitative observations.
Theoretical Analysis#
A theoretical analysis of a vision transformer (ViT) model would likely involve several key aspects. First, defining a tractable data model is crucial. This might involve simplifying the image data into a more manageable representation, potentially assuming a specific structure or distribution for the input features. This simplification allows the researchers to perform mathematical analysis. Next, analyzing the training dynamics is key, and it would focus on how the weights of the network evolve over time in response to the training data, based on the optimization algorithm and model architecture. Here, the analysis might include simplifying the attention mechanism and softmax activation to obtain analytical results. Furthermore, a generalization analysis would investigate the model’s ability to perform well on unseen data after training. Establishing bounds on test error would provide quantitative guarantees about the model’s performance on unseen data. Finally, the analysis might use tools from statistical learning theory or information theory to connect various properties of the ViT and its performance. The signal-to-noise ratio in the data is also a likely factor, impacting the model’s capability to generalize.
Future Work#
The paper’s conclusion suggests several promising avenues for future research. Extending the analysis to more complex transformer architectures beyond the two-layer model is crucial for broader applicability. The current model’s simplified structure, while enabling rigorous analysis, limits its generalizability to real-world scenarios. Investigating the role of different activation functions and attention mechanisms is important for understanding the training dynamics and generalization behavior in various settings. Exploring the influence of different initialization methods and loss functions is warranted for a thorough investigation of the benign overfitting phenomenon. Additionally, empirical validation on larger-scale vision datasets like ImageNet would significantly strengthen the theoretical findings. Finally, connecting this work’s theoretical insights to practical applications, such as improving the robustness and efficiency of training larger vision transformers, presents a compelling area of future work.
More visual insights#
More on figures

🔼 This figure shows the test loss of a two-layer vision transformer on synthetic data with different sample sizes (N) and signal-to-noise ratios (SNR). The heatmaps in (a) and (b) visualize the relationship between N, SNR, and test loss. A cutoff of 0.2 is applied in (b) to clearly distinguish between low and high test loss. The red curve represents the theoretical boundary (N * SNR^2 = 1000) separating the regions of benign and harmful overfitting.
read the caption
Figure 1: (a) is a heatmap of test loss on synthetic data across various signal-to-noise ratios (SNR) and sample sizes (N). High test losses are indicated with yellow, while low test losses are indicated with purple. (b) is a heatmap that applies a cutoff value 0.2. It categorizes values below 0.2 as 0 (purple), and above 0.2 as 1 (yellow). The expression for the red curves in (a) and (b) is N · SNR² = 1000.

🔼 This figure shows the test loss results on synthetic data across various sample sizes (N) and signal-to-noise ratios (SNR). The heatmap in (a) visualizes the test loss, with yellow representing high loss and purple representing low loss. A cutoff value of 0.2 is applied in (b), categorizing losses below 0.2 as 0 (purple) and above 0.2 as 1 (yellow). The red curve represents N · SNR² = 1000, indicating the theoretical boundary between benign and harmful overfitting regimes.
read the caption
Figure 1: (a) is a heatmap of test loss on synthetic data across various signal-to-noise ratios (SNR) and sample sizes (N). High test losses are indicated with yellow, while low test losses are indicated with purple. (b) is a heatmap that applies a cutoff value 0.2. It categorizes values below 0.2 as 0 (purple), and above 0.2 as 1 (yellow). The expression for the red curves in (a) and (b) is N · SNR2 = 1000.
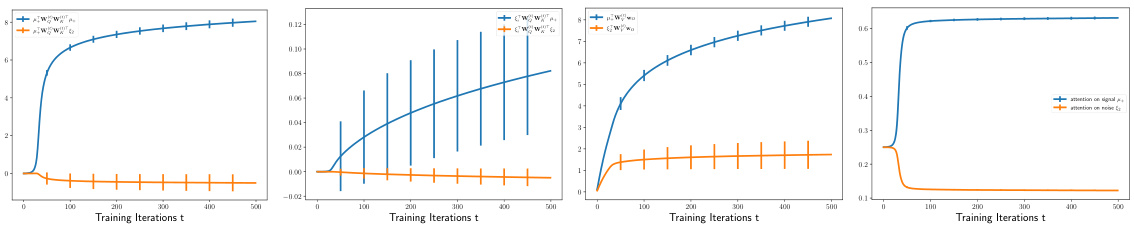
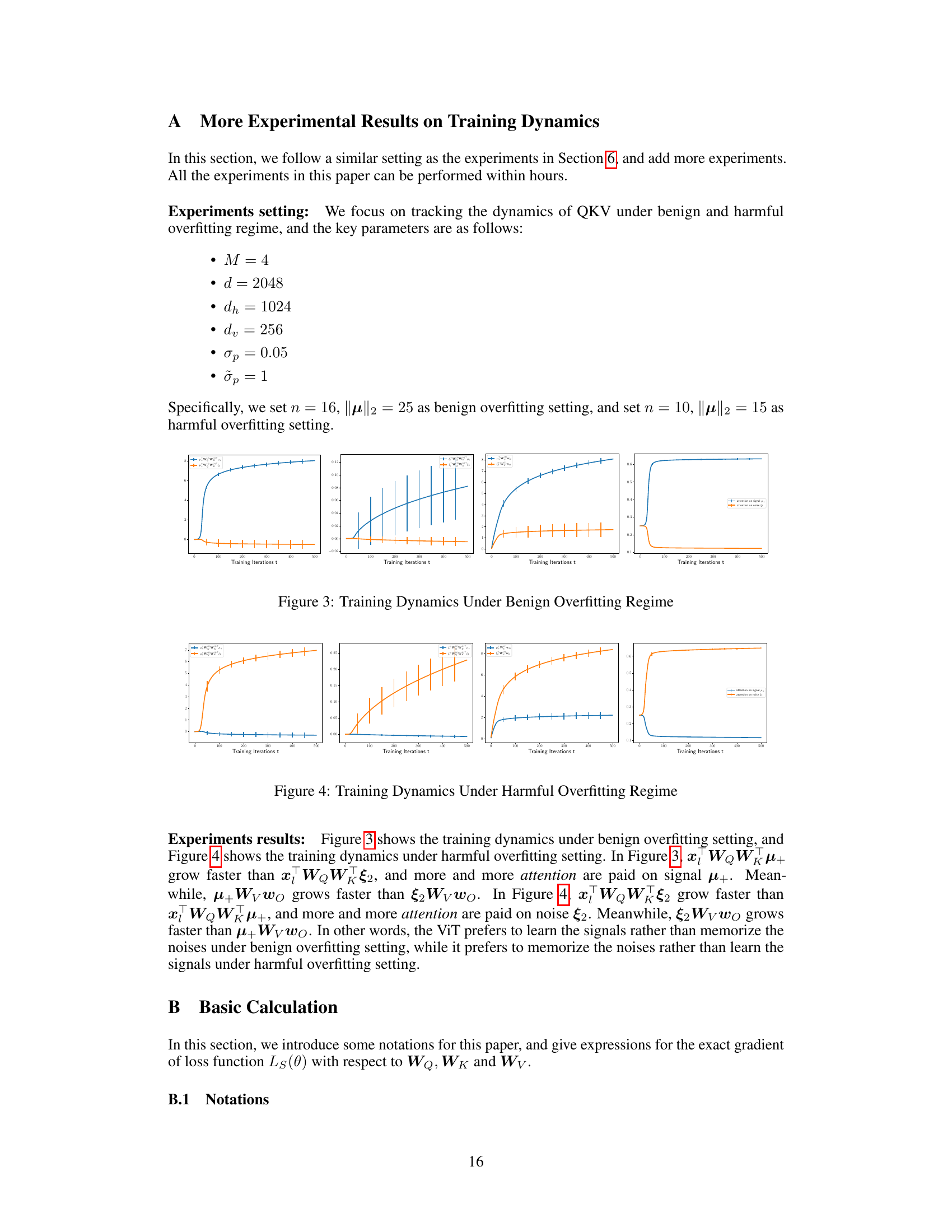
🔼 This figure shows the training dynamics of the weights of the two-layer transformer model under the benign overfitting regime. Four subfigures display the training dynamics of the query (WQ), key (WK), and value (WV) matrices and the linear layer weight vector (wo), along with their 2-sigma error bars. The plots illustrate how the weights evolve over training iterations, demonstrating a clear separation between the dynamics of weights that focus on signal tokens versus those focusing on noise tokens. In the benign overfitting scenario, the model is able to successfully generalize well despite overfitting to training data, which is indicated by the small test error that remains low throughout the training.
read the caption
Figure 3: Training Dynamics Under Benign Overfitting Regime
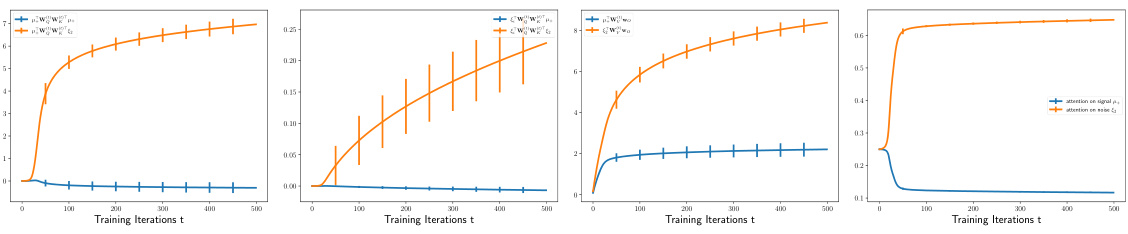
🔼 The figure shows the training dynamics of a vision transformer under a benign overfitting regime. It displays the evolution of several key quantities over training iterations. Notably, the attention paid to signal tokens increases significantly, while the attention given to noise tokens decreases. The model’s ability to correctly learn signals is clearly depicted by the trend of the curves.
read the caption
Figure 3: Training Dynamics Under Benign Overfitting Regime
Full paper#