↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large Language Models (LLMs) are computationally expensive. A common approach to reduce this cost is pruning, removing less important parameters. Existing LLM pruning methods typically apply uniform pruning across all layers, limiting their effectiveness. Furthermore, existing layerwise methods often rely on heuristics, potentially leading to suboptimal performance. This paper addresses these issues by developing a more sophisticated approach.
This paper introduces AlphaPruning, a novel layer-wise pruning method. It leverages “Heavy-Tailed Self-Regularization (HT-SR)” theory, analyzing the distribution of weight matrix eigenvalues to determine optimal pruning ratios for each layer. Experiments show AlphaPruning outperforms existing methods, achieving significantly higher sparsity (80% in LLaMA-7B) while preserving model accuracy. The work also demonstrates the generalizability of the method by integrating it with other LLM compression techniques and extending it to Computer Vision (CV) models. The code is open-sourced.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on LLM optimization and efficiency. It introduces a novel, theoretically-grounded approach to layer-wise pruning, achieving significantly higher sparsity levels than previously possible while maintaining performance. This opens exciting avenues for reducing the computational cost and memory footprint of LLMs, making them more accessible for broader applications and resource-constrained settings. The proposed method’s generalizability across various architectures and its integration with other compression techniques further enhance its significance.
Visual Insights#
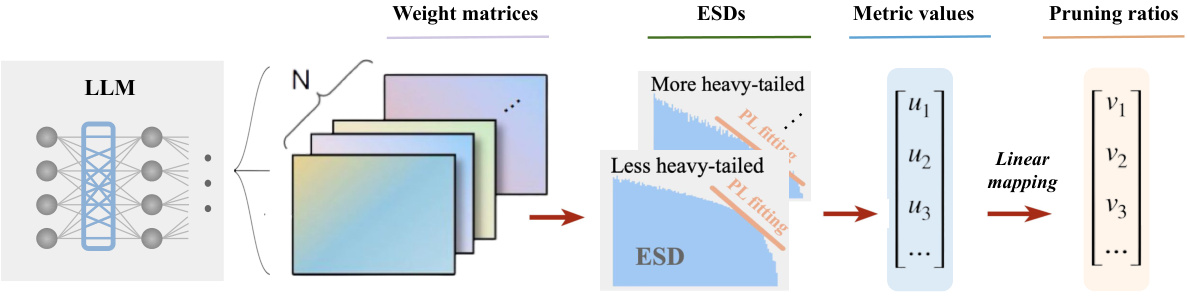
This figure illustrates the AlphaPruning pipeline, a post-training layer-wise pruning method for LLMs. It shows three main stages: 1) ESD analysis of the weight matrices in each layer of the LLM to assess their heavy-tailed properties (measured by the HT exponent); 2) PL fitting to quantify the heavy-tailedness of each layer’s ESD; 3) A linear mapping function that transforms the layer-wise quality metrics (derived from PL fitting) into layer-wise pruning ratios, which are then applied to prune the LLM.

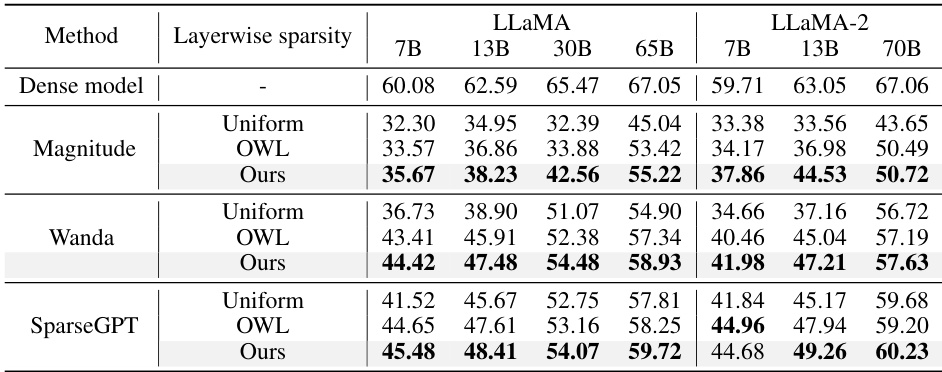
This table compares the performance of different metrics (shape vs. scale) for allocating layer-wise sparsity in LLMs. It shows the WikiText perplexity and average accuracy across seven zero-shot tasks when using various metrics in conjunction with three different intra-layer pruning methods (Magnitude, Wanda, and SparseGPT). The results demonstrate the superiority of shape metrics, particularly PL_Alpha_Hill, for guiding sparsity allocation.
In-depth insights#
HT-SR in LLM Pruning#
The application of Heavy-Tailed Self-Regularization (HT-SR) theory to Large Language Model (LLM) pruning offers a novel, theoretically-grounded approach to enhance the effectiveness of pruning strategies. HT-SR focuses on the shape of the empirical spectral densities (ESDs) of weight matrices within LLMs. The theory posits that well-trained layers exhibit heavy-tailed ESDs, indicating stronger correlations among weights and signifying higher quality. By leveraging this insight, AlphaPruning, a method introduced in this paper, allocates pruning ratios based on layer-wise ESD shape metrics. This theoretically-principled method moves beyond heuristic-based layerwise pruning, achieving improved results compared to uniform pruning and existing non-uniform approaches. Importantly, AlphaPruning demonstrates the power of shape metrics over scale metrics in guiding effective sparsity allocation. This finding highlights a new perspective on LLM pruning. The success of AlphaPruning in achieving high sparsity levels (e.g., 80% in LLaMA-7B) while maintaining reasonable performance underscores the potential of HT-SR theory in optimizing LLM compression.
AlphaPruning Method#
The AlphaPruning method presents a novel approach to layer-wise pruning of large language models (LLMs). It leverages Heavy-Tailed Self-Regularization (HT-SR) theory, analyzing the empirical spectral densities (ESDs) of weight matrices to determine layer-wise pruning ratios. Unlike uniform pruning strategies, AlphaPruning allocates sparsity based on the shape of ESDs, specifically utilizing the Hill estimator to quantify the heavy-tailed nature. This principled approach ensures that well-trained layers with strong correlations among weight matrix elements (indicated by lower PL_Alpha_Hill values) are pruned less aggressively. AlphaPruning’s key innovation is its theoretically-grounded layer-wise sparsity allocation, moving beyond heuristic methods and offering superior performance compared to existing LLM pruning techniques. This is demonstrated through empirical results showing that it effectively reduces perplexity and maintains reasonable performance even at high sparsity levels (80% in the case of LLaMA-7B), achieving a first in LLM pruning.
Sparsity Allocation#
The core of the AlphaPruning method lies in its novel approach to sparsity allocation. Instead of uniformly distributing sparsity across all layers, which limits the overall pruning potential, AlphaPruning leverages the Heavy-Tailed Self-Regularization (HT-SR) theory. This theory reveals a significant variability in the “prunability” of different layers within a large language model (LLM), as determined by the shape of their weight matrices’ empirical spectral densities (ESDs). AlphaPruning uses a theoretically-principled approach by employing shape metrics, specifically the power-law exponent of the fitted ESD, as a measure of layer quality. Layers with more pronounced heavy-tailed ESDs, indicative of higher quality and robustness, are allocated less sparsity, preserving their valuable information. This layer-wise sparsity allocation strategy surpasses uniform methods by achieving higher overall sparsity levels while maintaining reasonable performance. The superior performance of AlphaPruning’s approach is shown to be robust, generalizable across different LLM architectures, and it can be integrated with other compression methods.
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims and hypotheses presented in the introduction. A robust empirical results section should begin with a clear description of the experimental setup, including the datasets used, the evaluation metrics, and the baseline methods compared against. It’s critical to present results clearly and systematically, often using tables and figures to visualize the findings. Key aspects to consider are the statistical significance of the results, ensuring that observed differences are not due to random chance. The discussion should go beyond simply reporting the numbers; it needs to interpret the results in the context of the paper’s hypotheses, pointing out successes, failures, and any unexpected outcomes. Furthermore, a good empirical results section will address potential limitations, such as dataset biases or model specificities, and suggest avenues for future work.
Future of Pruning#
The future of pruning neural networks hinges on several key areas. Developing more sophisticated algorithms that move beyond simple magnitude-based pruning is crucial. This includes exploring methods that consider the network’s architecture, the importance of individual connections for specific tasks, and the broader context of the network’s learned representations. Integrating pruning with other compression techniques, such as quantization and knowledge distillation, will become increasingly important to maximize efficiency gains. Addressing the challenge of fine-tuning pruned models while maintaining or improving performance is another critical area, and research into methods that require minimal or no retraining are highly desired. Finally, theoretical understanding will play a vital role. Advancing our theoretical understanding of how pruning affects network learning dynamics will facilitate the development of more robust and effective algorithms. This requires the use of advanced mathematical tools and rigorous testing to develop a predictive theory of pruning.
More visual insights#
More on figures

This figure compares the performance of LLaMA-7B and LLaMA-13B models pruned using the Wanda method with different sparsity levels. The x-axis represents the sparsity percentage (how many parameters were removed), and the y-axis shows the WikiText validation perplexity, a measure of how well the model predicts the next word in a sequence. Lower perplexity indicates better performance. The figure shows that AlphaPruning consistently outperforms the uniform sparsity approach across different sparsity levels for both models.
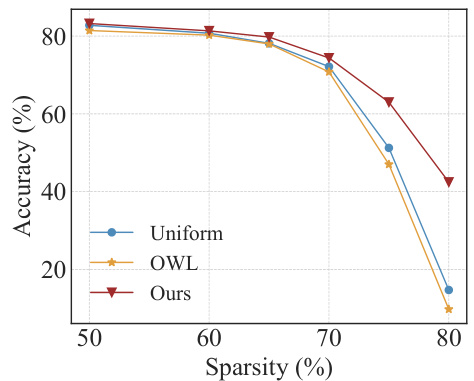
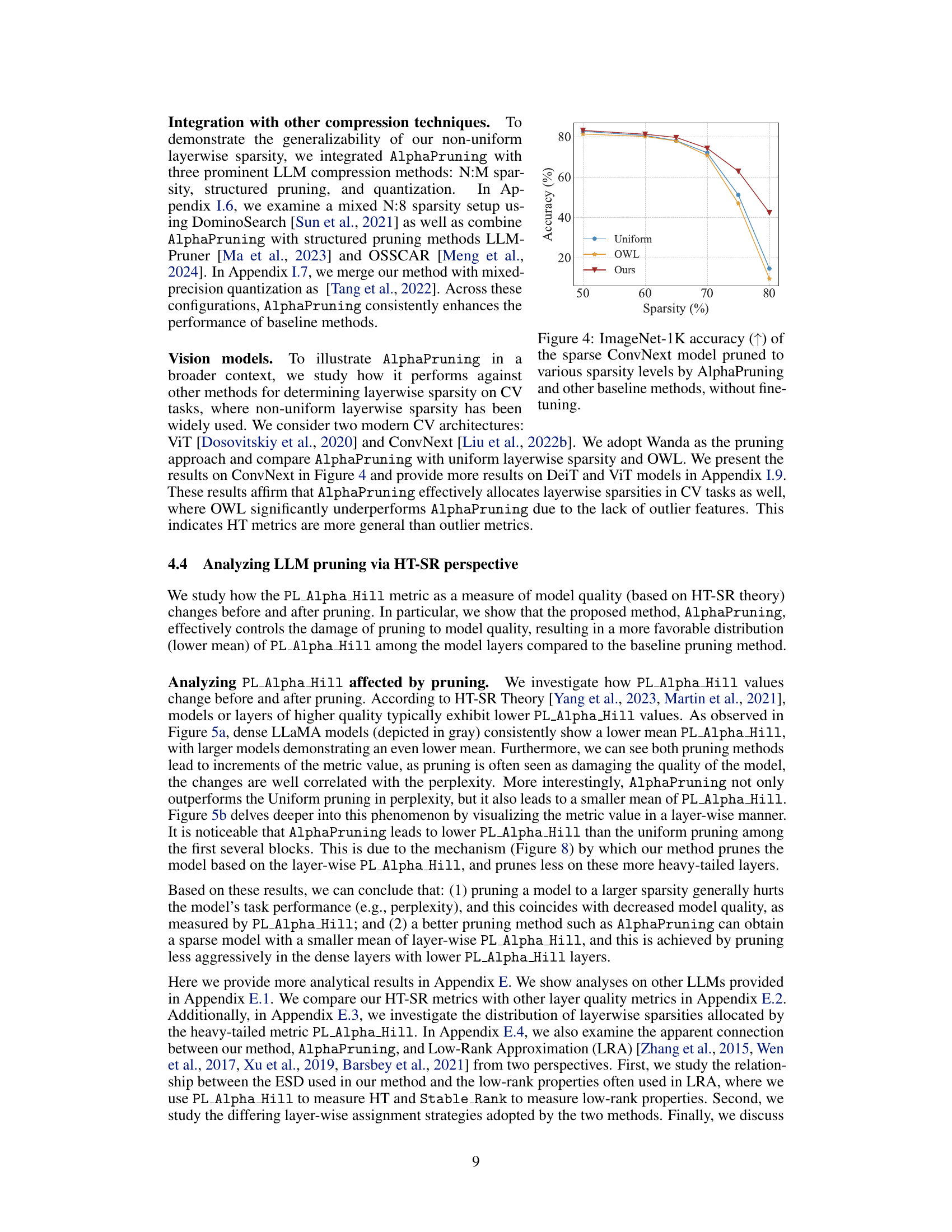
This figure compares the performance of AlphaPruning against other baseline methods in pruning a ConvNext model on the ImageNet-1K dataset. The x-axis represents the sparsity level (percentage of weights removed), and the y-axis shows the ImageNet-1K accuracy. The results demonstrate the superior performance of AlphaPruning in maintaining accuracy even at high sparsity levels, outperforming uniform sparsity and OWL methods.
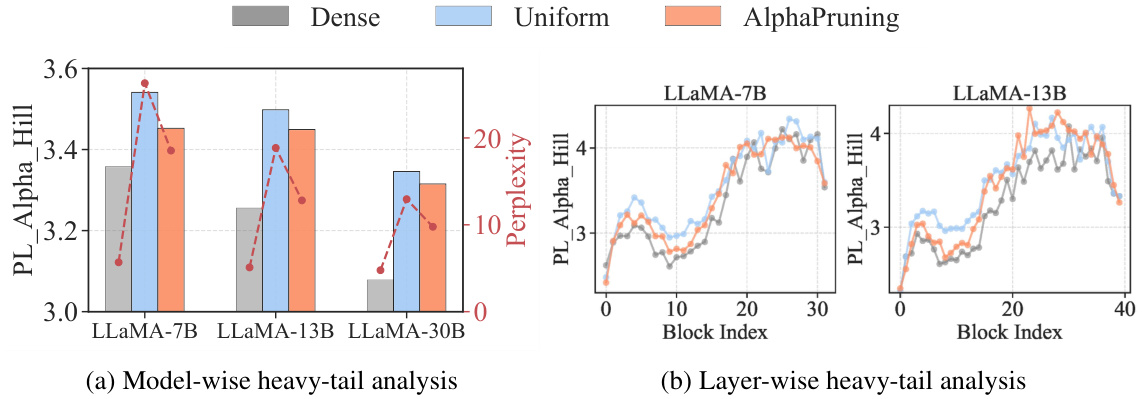
This figure shows the results of analyzing the heavy-tailed self-regularization (HT-SR) properties of LLMs before and after pruning using both uniform and AlphaPruning methods. Subfigure (a) compares the average PL_Alpha_Hill metric (a measure of model quality) and perplexity across different LLM sizes (7B, 13B, 30B parameters). It demonstrates that AlphaPruning maintains better model quality (lower PL_Alpha_Hill) compared to uniform pruning, resulting in lower perplexity. Subfigure (b) provides a layer-wise analysis of the PL_Alpha_Hill metric for LLaMA-7B and LLaMA-13B models, showing AlphaPruning’s more targeted pruning approach.
This figure shows a comparison of the heavy-tailed metric PL_Alpha_Hill and the WikiText validation perplexity before and after applying uniform pruning and AlphaPruning. Subfigure (a) provides a model-wise comparison, averaging the PL_Alpha_Hill across all layers for each model. The dashed line shows the perplexity, while the histogram displays the PL_Alpha_Hill distribution. Subfigure (b) offers a layer-wise comparison, with the PL_Alpha_Hill averaged across all matrices within each LLM layer. The lower the PL_Alpha_Hill, the better the model quality according to HT-SR theory.

This figure compares the layer-wise sparsity distributions obtained from AlphaPruning and OWL methods. Both methods show a general trend of lower sparsity in earlier layers and higher sparsity in later layers, which is intuitive given the typical importance of early layers in LLMs. However, AlphaPruning shows a more fine-grained distribution with more distinct differences in sparsity between adjacent layers compared to OWL.
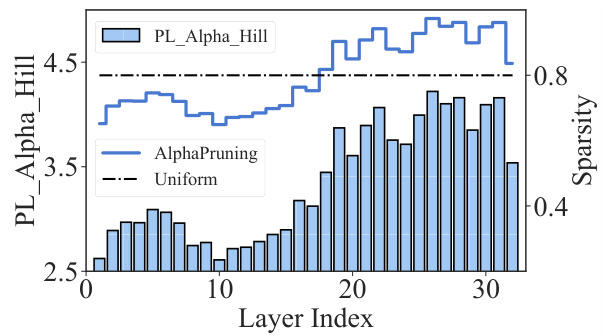
This figure compares the heavy-tailed metric PL_Alpha_Hill and the WikiText validation perplexity before and after pruning using uniform pruning and AlphaPruning methods. Panel (a) shows model-wide comparison by averaging PL_Alpha_Hill across all layers, demonstrating that AlphaPruning maintains better model quality than uniform pruning, as reflected by lower perplexity and PL_Alpha_Hill values. Panel (b) provides a layer-wise analysis showing that AlphaPruning preserves the quality of model layers more effectively.
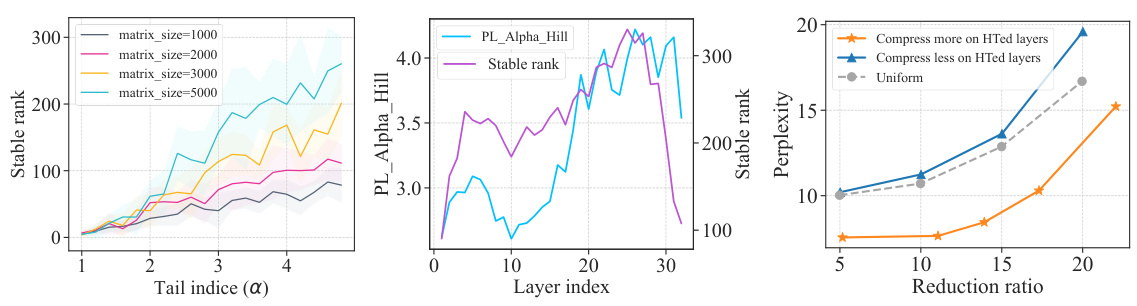
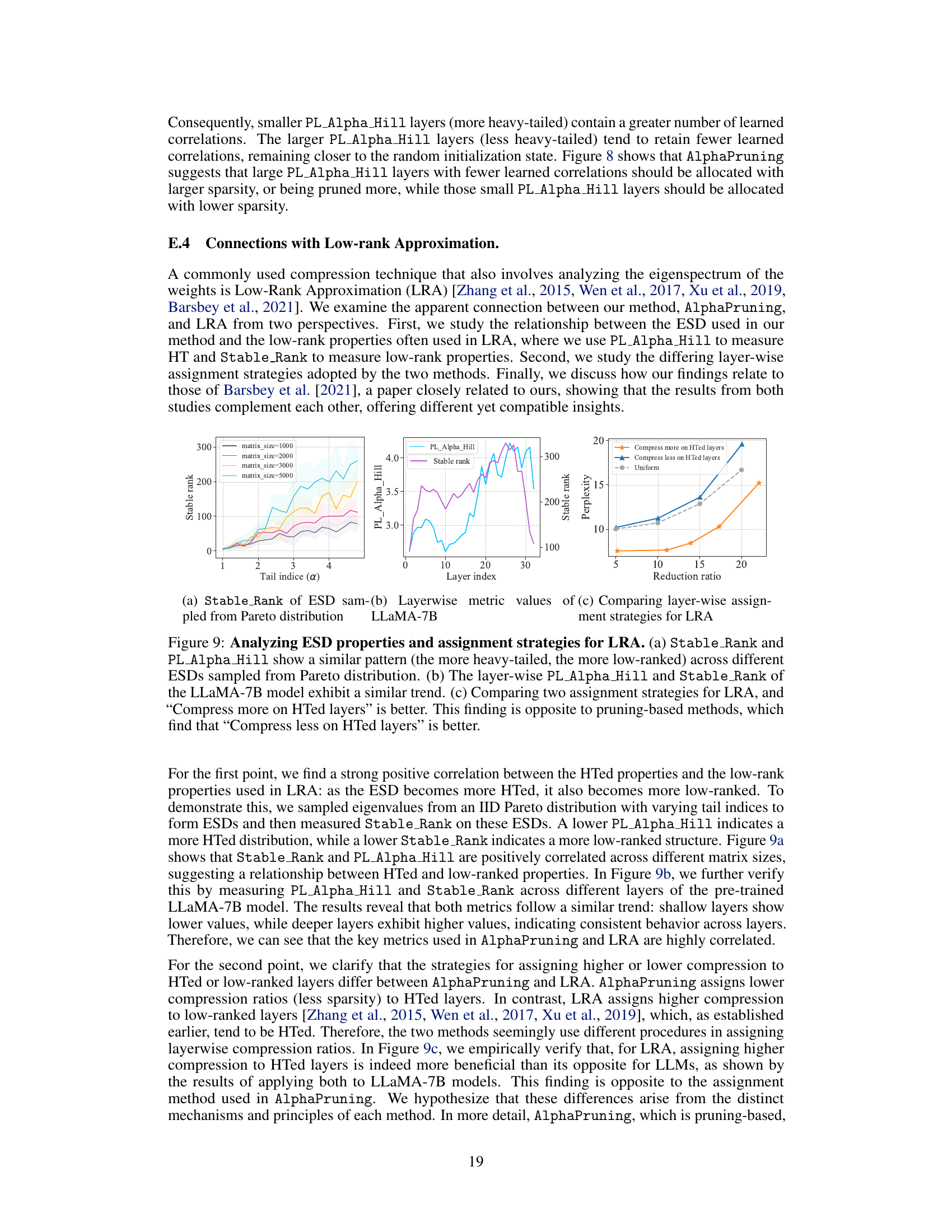
This figure compares the heavy-tailed (HT) properties and low-rank properties of weight matrices in LLMs. It shows a strong positive correlation between these properties: more heavy-tailed matrices are also more low-ranked. The figure further explores layer-wise patterns in these properties within the LLaMA-7B model, demonstrating a similarity between heavy-tailed and low-rank structures across layers. Finally, the figure contrasts two LRA assignment strategies, revealing that prioritizing compression on heavier-tailed layers yields superior results, contrasting with the findings of pruning-based methods.
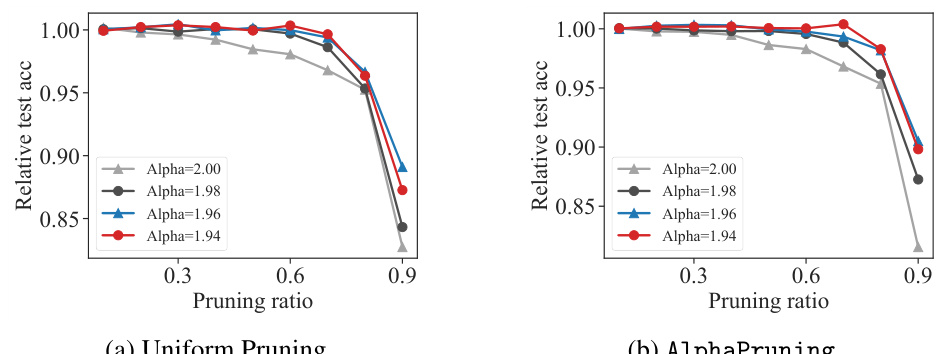
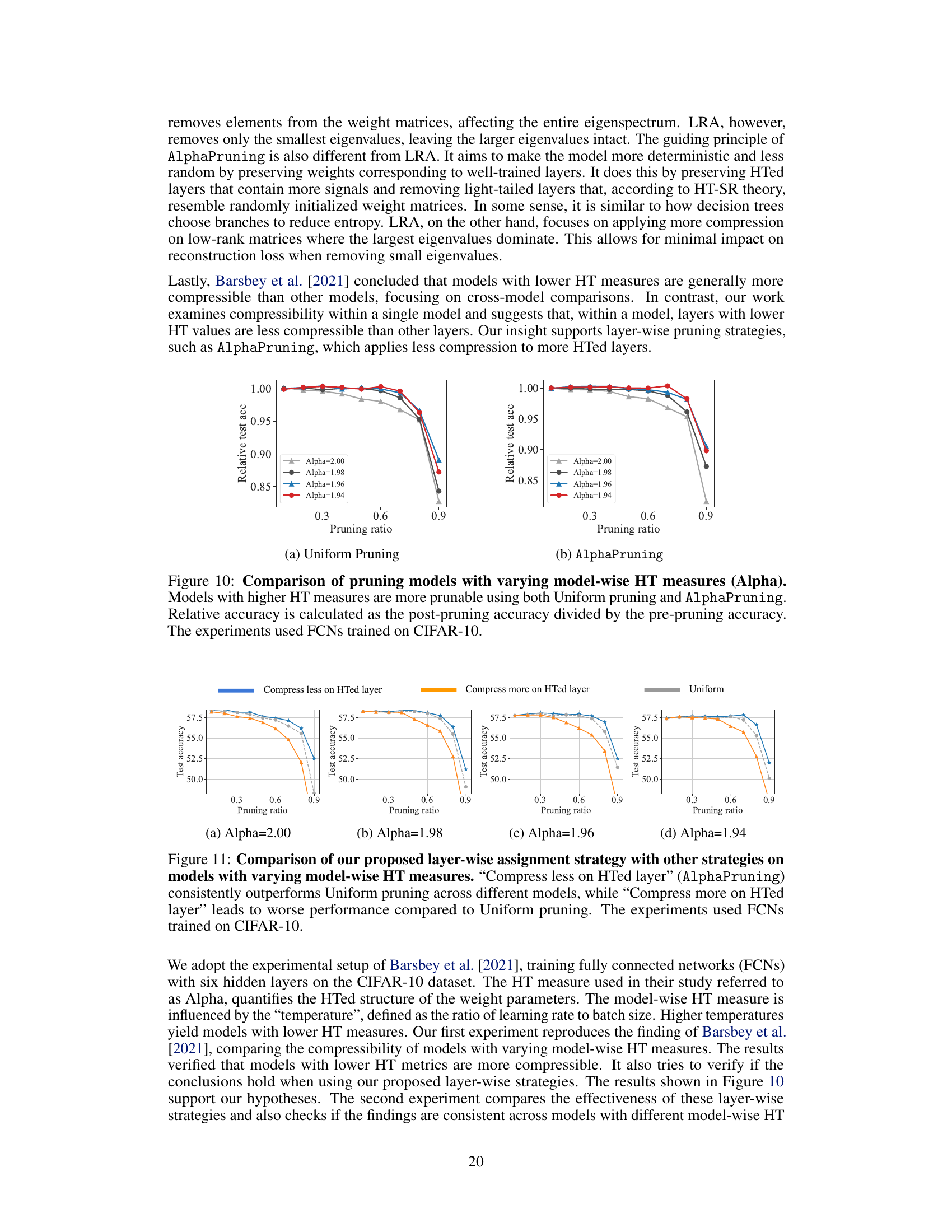
This figure shows the results of an experiment comparing the performance of two pruning methods (uniform pruning and AlphaPruning) on fully connected neural networks (FCNs) trained on the CIFAR-10 dataset. The x-axis represents the pruning ratio, and the y-axis shows the relative test accuracy (post-pruning accuracy / pre-pruning accuracy). Different colored lines represent FCNs with varying heavy-tailed (HT) measures (Alpha), a metric used to characterize the heavy-tailedness of the weight matrix eigenspectrum, which is related to the model’s training quality and generalization capabilities. The results demonstrate that models with higher HT measures are generally more prunable, meaning that a larger fraction of their parameters can be removed without significant performance degradation, using both uniform and AlphaPruning methods.

This figure shows the result of comparing two pruning strategies (uniform pruning and AlphaPruning) on fully connected networks (FCNs) trained with different model-wise heavy-tailed (HT) measures (Alpha). The x-axis represents the pruning ratio and the y-axis represents the relative test accuracy, calculated by dividing the post-pruning test accuracy by the pre-pruning test accuracy. The results demonstrate that models with higher HT measures are more easily pruned using both uniform and AlphaPruning methods. The experiments were conducted using FCNs and the CIFAR-10 dataset.
This figure compares the layer-wise sparsity distributions produced by AlphaPruning and OWL. Both methods show a general trend of lower sparsity in earlier layers and higher sparsity in later layers, but AlphaPruning demonstrates a more nuanced distribution. AlphaPruning’s distribution is more granular, with more noticeable differences in sparsity between consecutive layers, suggesting a more refined allocation of sparsity based on the model’s structure and training characteristics.
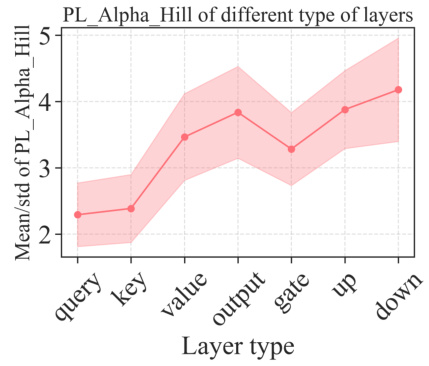
This figure analyzes the heavy-tailed self-regularization (HT-SR) metric PL_Alpha_Hill and its correlation with the WikiText validation perplexity before and after pruning using uniform pruning and AlphaPruning. It shows that AlphaPruning not only outperforms uniform pruning in terms of perplexity but also leads to a more favorable distribution (lower mean) of PL_Alpha_Hill among the layers, minimizing the damage caused by pruning.

This figure shows the pipeline of AlphaPruning, a post-training layer-wise pruning method. It consists of three main steps: 1) analyzing the empirical spectral densities (ESDs) of all weight matrices in the base large language model (LLM), 2) fitting power laws (PL) to the ESDs to obtain layer-wise metric values (representing the heavy-tailed exponent), and 3) using these metric values to linearly map the layer-wise pruning ratios. The diagram visually depicts the flow of information from the weight matrices through ESD analysis and PL fitting to the final pruning ratios allocated to each layer.

This figure illustrates the pipeline of AlphaPruning, a post-training layer-wise pruning method. It starts with analyzing the empirical spectral densities (ESDs) of the weight matrices of a large language model (LLM). Then, power-law (PL) fitting is used to extract metric values that represent the heavy-tailed property of each layer. Finally, a linear mapping function applies these metric values to determine layer-wise pruning ratios, which means each layer of the LLM is pruned with a different ratio.
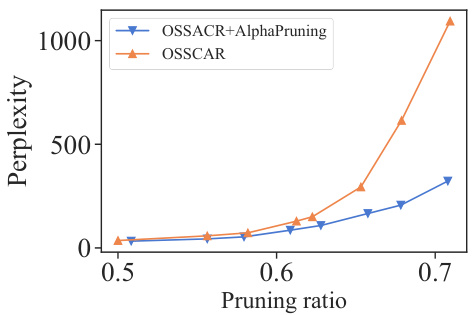
This figure compares the performance of OSSCAR with and without AlphaPruning. OSSCAR is a structured pruning method that prunes parameters within specific layers (linear sublayer of multi-head attention and second sublayer of the feed-forward network). AlphaPruning allocates sparsity non-uniformly across layers, while OSSCAR uses uniform pruning. The x-axis represents the pruning ratio (fraction of pruned parameters relative to the total number in the specified layers), and the y-axis is the perplexity of the OPT-6.7B model evaluated on WikiText. Lower perplexity indicates better performance. The graph shows that AlphaPruning combined with OSSCAR consistently achieves lower perplexity than OSSCAR alone across different pruning ratios, demonstrating its effectiveness in improving the performance of this structured pruning method.
More on tables
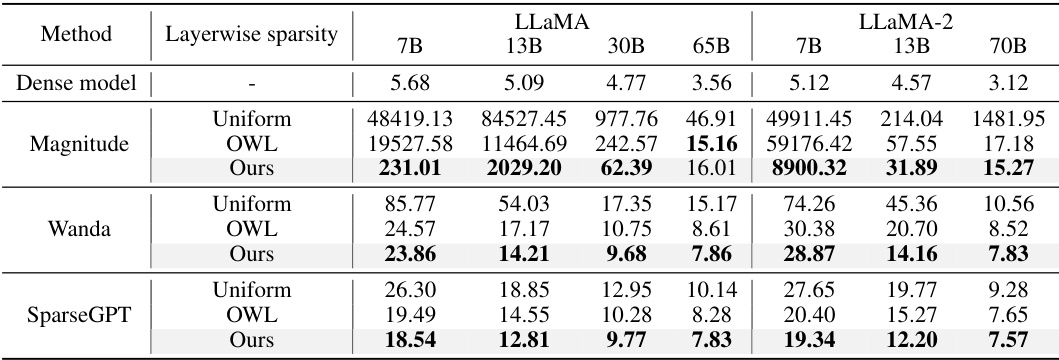
This table compares the WikiText validation perplexity of LLaMA and LLaMA-2 models pruned to 70% sparsity using different methods. The methods compared include AlphaPruning (the proposed method), uniform layerwise sparsity, and OWL (a state-of-the-art non-uniform sparsity allocation method). Each of these methods is combined with three different intra-layer pruning techniques: Magnitude, Wanda, and SparseGPT. Lower perplexity scores indicate better model performance.
This table shows the WikiText validation perplexity for different LLMs (LLaMA and LLaMA-2) pruned to 70% sparsity using different methods. The methods compared are AlphaPruning (the proposed method), uniform layerwise sparsity, and OWL (a state-of-the-art non-uniform sparsity allocation method). Each of these sparsity allocation methods is combined with three different intra-layer pruning techniques: Magnitude, Wanda, and SparseGPT. Lower perplexity values indicate better performance.

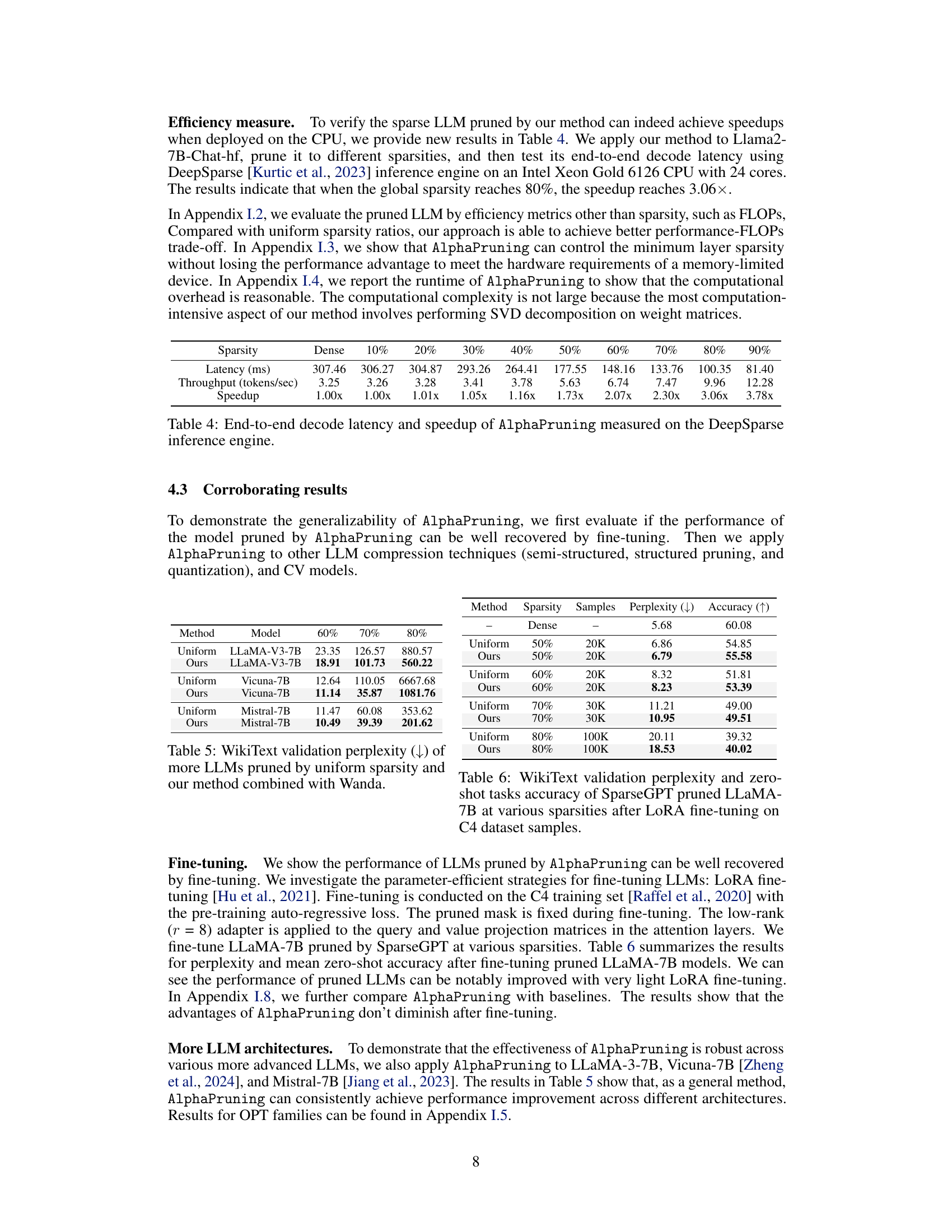
This table presents the results of measuring the end-to-end decode latency and speedup of the AlphaPruning method on the DeepSparse inference engine. The results show the decode latency and speedup at various sparsity levels (from 10% to 90%). The speedup is calculated relative to the dense model (1.00x). The table demonstrates that AlphaPruning achieves significant speedups at higher sparsity levels, reaching a 3.06x speedup at 80% sparsity.
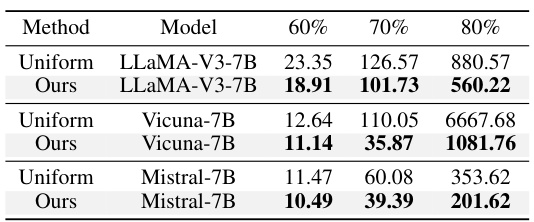
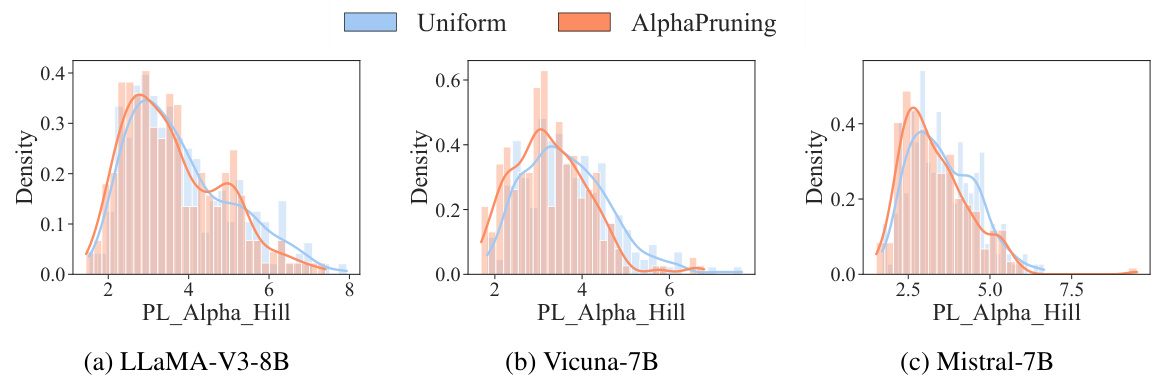
This table compares the performance of AlphaPruning against uniform sparsity and OWL on various LLMs. The perplexity (a measure of how well a model predicts text) is shown for different levels of sparsity (60%, 70%, 80%), for each of the models listed (LLaMA-V3-7B, Vicuna-7B, and Mistral-7B). Lower perplexity indicates better performance after pruning. The results demonstrate that AlphaPruning consistently outperforms the other methods, especially at higher sparsity levels.

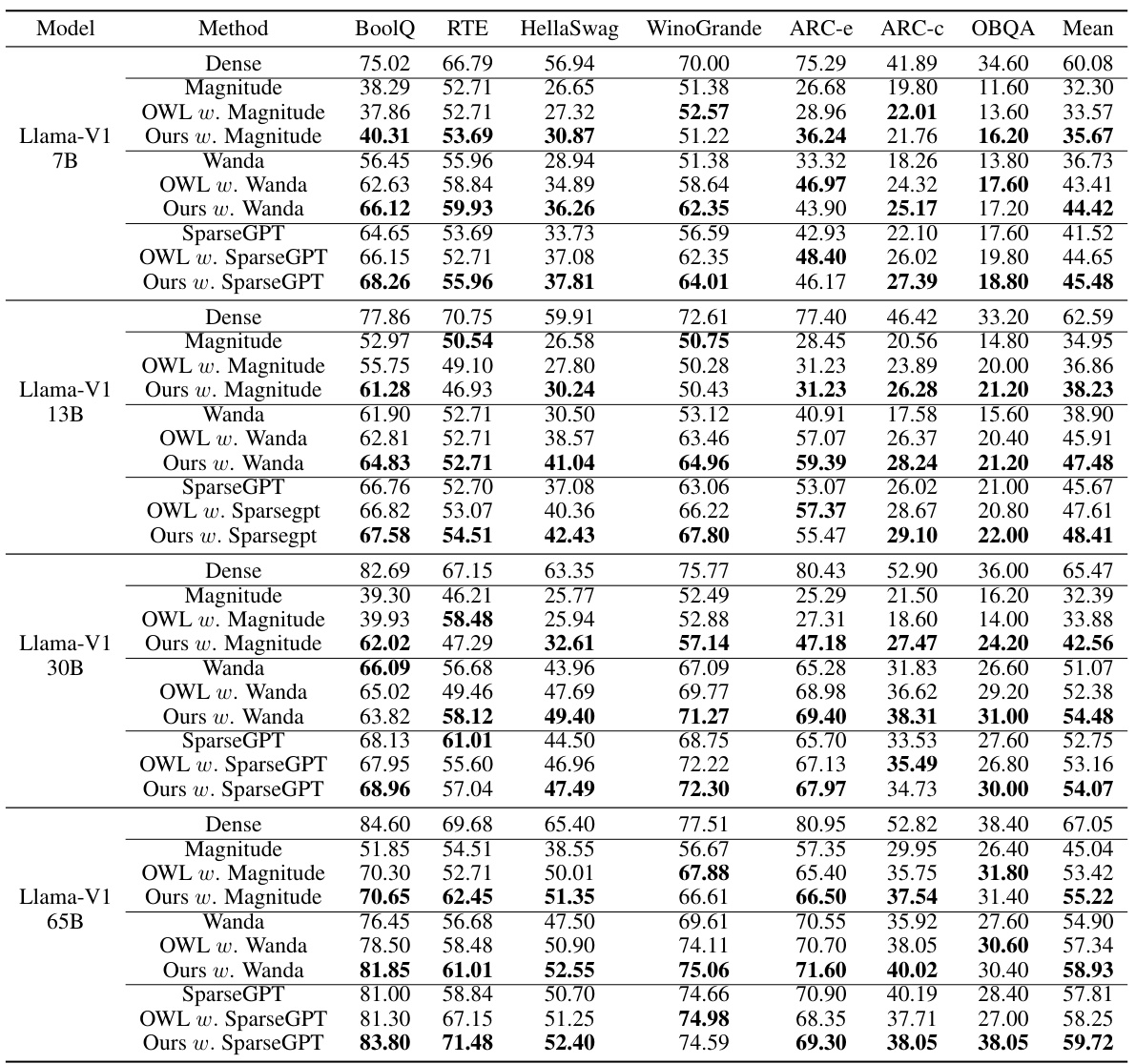
This table compares the WikiText validation perplexity and accuracy of several LLMs pruned using uniform sparsity and AlphaPruning, both combined with the Wanda pruning method. It demonstrates the effectiveness of AlphaPruning across various model sizes and architectures, showing that it consistently improves perplexity (lower is better) and often increases accuracy (higher is better) at high sparsity levels (60%, 70%, 80%). The results highlight the generalizability of AlphaPruning.

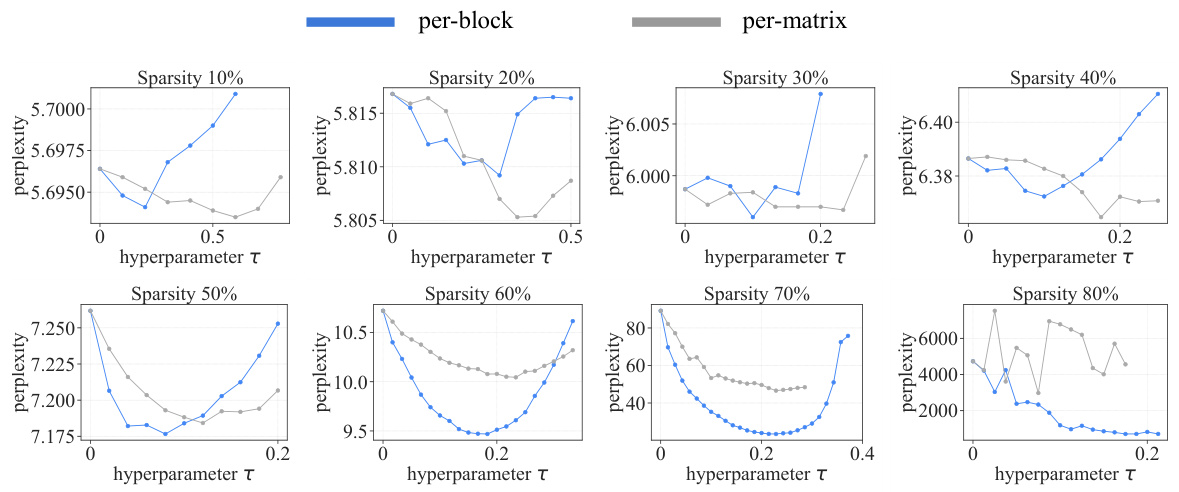
This table compares the perplexity results of LLaMA-7B pruned to 70% sparsity using four different sparsity allocation methods: Uniform, Per-matrix, Per-block, and Mixed. The perplexity is measured using the WikiText validation set. Each sparsity allocation method is combined with three different pruning methods: Magnitude, Wanda, and SparseGPT. The table highlights the superior performance of the proposed ‘Mixed’ method.
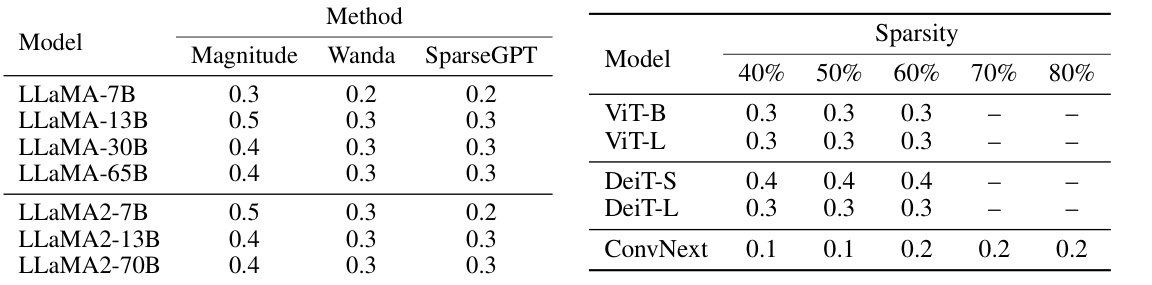
This table shows the hyperparameter settings used in the experiments. The left part shows the optimal τ values used for the experiments in Section 4.2, which were obtained through a small hyperparameter sweep. The right part shows the optimal τ values used for the experiments in Section 4.3 involving Vision Transformers, which were also obtained via a hyperparameter sweep. The experiments in section 4.2 involve language models, while the experiments in section 4.3 involve vision models, and the different hyperparameter ranges reflect differences in model architectures and tasks.
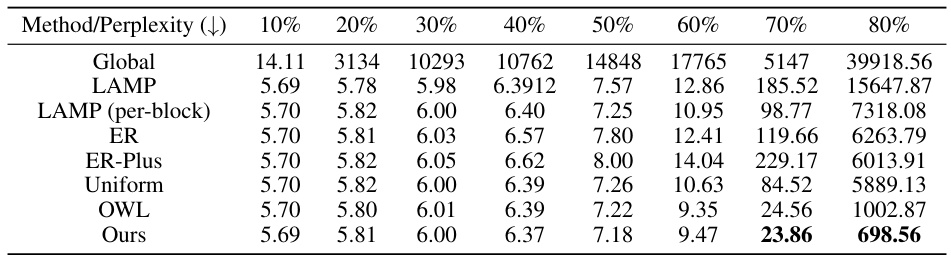
This table presents the WikiText validation perplexity results for the LLaMA-7B model pruned using different layer-wise sparsity allocation methods at various global sparsity levels (10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%). The methods compared include Uniform, Global, LAMP, ER, ER-Plus, OWL, and the proposed AlphaPruning method. Lower perplexity values indicate better performance. The table highlights that AlphaPruning consistently achieves lower perplexity than other methods, particularly at higher sparsity levels.
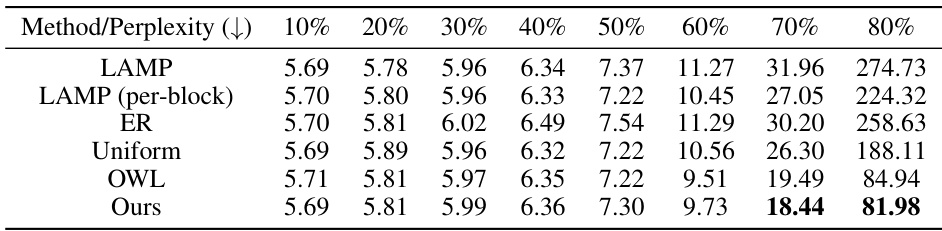
This table compares the WikiText validation perplexity of pruned LLaMA and LLaMA-2 models at 70% sparsity using different methods. The methods compared include AlphaPruning (the proposed method), uniform layerwise sparsity, and OWL. Each of these is combined with three different intra-layer pruning techniques (Magnitude, Wanda, and SparseGPT). Lower perplexity values indicate better model performance after pruning.

This table compares the performance of various heavy-tailed self-regularization (HT-SR) metrics for allocating layer-wise sparsity in LLMs. It uses WikiText perplexity and average accuracy across seven zero-shot tasks to evaluate the effectiveness of different metrics when pruning the LLaMA-7B model to 70% sparsity. The results highlight that shape metrics generally outperform scale metrics, with PL_Alpha_Hill showing the best performance.
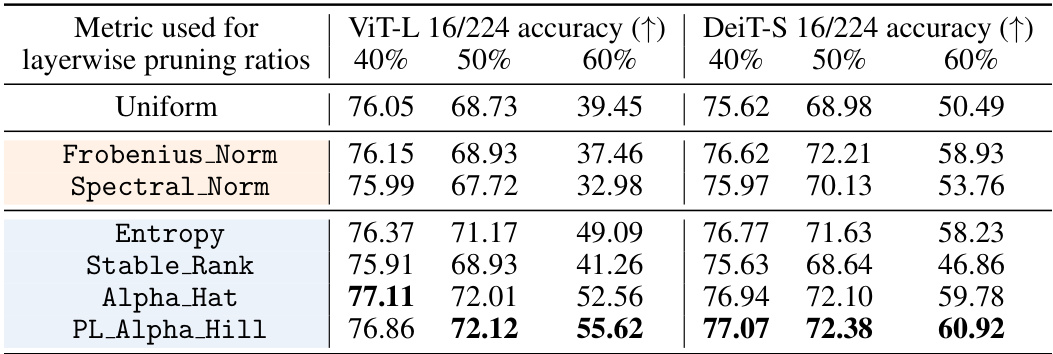
This table compares the performance of various heavy-tailed self-regularization (HT-SR) metrics for guiding layer-wise sparsity allocation in Large Language Models (LLMs). It uses WikiText perplexity and average accuracy across seven zero-shot tasks to evaluate the effectiveness of different metrics (shape vs. scale). The results demonstrate that shape metrics significantly outperform scale metrics in assigning layer-wise sparsity, with PL_Alpha_Hill showing the best performance.

This table compares the performance of various heavy-tailed self-regularization (HT-SR) metrics in assigning layer-wise sparsity for Large Language Models (LLMs). It uses WikiText perplexity and accuracy across seven zero-shot tasks to evaluate the performance of LLaMA-7B model pruned to 70% sparsity using different metrics. The results demonstrate that shape metrics generally outperform scale metrics, with PL_Alpha_Hill being the most effective metric.
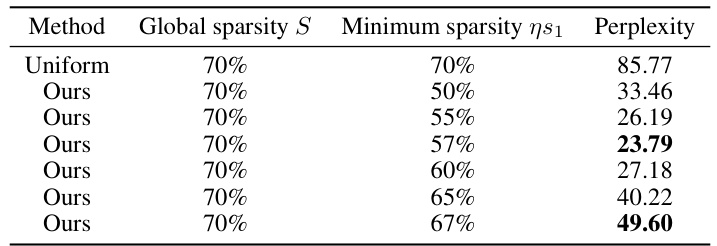
This table shows the results of adjusting the minimum sparsity while maintaining the global sparsity at 70%. It compares the WikiText validation perplexity achieved by the AlphaPruning method with different minimum sparsity levels (50%, 55%, 57%, 60%, 65%, 67%) to the Uniform method’s perplexity. The results highlight that AlphaPruning consistently achieves lower perplexity even when the minimum sparsity is increased, demonstrating its robustness and effectiveness in controlling the minimum layer sparsity for memory-limited hardware.

This table compares different metrics for allocating layerwise sparsity in LLMs. It shows that shape metrics, which describe the shape of the ESDs of the weight matrices, outperform scale metrics, which measure the size of the ESDs. The PL_Alpha_Hill metric performs the best. The experiment is conducted on the LLaMA-7B model with 70% sparsity, measuring both WikiText validation perplexity and average accuracy across seven zero-shot tasks.

This table compares the perplexity results of OPT models (OPT-125M, OPT-350M, OPT-2.7B, and OPT-6.7B) pruned using two methods: uniform sparsity and the proposed AlphaPruning method combined with magnitude-based pruning. The perplexity scores are provided for 40% and 50% sparsity levels. Lower perplexity values indicate better model performance after pruning.

This table compares the perplexity of OPT models (OPT-125M, OPT-350M, OPT-2.7B, OPT-6.7B) pruned using two different methods: uniform sparsity and the proposed AlphaPruning method combined with Wanda and SparseGPT. For each model, perplexity is shown at 70% sparsity. The results demonstrate that AlphaPruning, when combined with Wanda and SparseGPT, generally yields lower perplexity scores compared to using a uniform sparsity allocation strategy, indicating that the proposed method is more effective at preserving model performance during pruning.

This table compares the performance of different sparsity allocation methods for pruning LLaMA-7B using the Wanda pruning technique. The methods compared are uniform sparsity, and the proposed AlphaPruning method which uses a mixed N:8 sparsity strategy. The results are reported for different sparsity levels (4:8, 3:8, 2:8) and indicate the WikiText validation perplexity for each scenario. The table demonstrates that AlphaPruning outperforms uniform sparsity allocation across various sparsity levels, leading to significant performance improvements.

This table compares the performance of applying AlphaPruning with LLM Pruner on the WikiText and Penn Treebank datasets at different sparsity levels (20%, 40%, 60%, 80%). It shows that AlphaPruning consistently improves the model’s performance in terms of lower perplexity across various sparsity levels when compared against uniform pruning strategies.

This table compares the WikiText validation perplexity of pruned LLaMA and LLaMA-2 models at 70% sparsity using different layerwise sparsity allocation methods. The methods compared are AlphaPruning (the proposed method), uniform layerwise sparsity, and OWL (a state-of-the-art non-uniform method). Each of these sparsity allocation methods was combined with three different intra-layer pruning techniques: Magnitude, Wanda, and SparseGPT. Lower perplexity values indicate better model performance after pruning.

This table compares the WikiText validation perplexity of pruned LLaMA and LLaMA-2 models at 70% sparsity using different methods. The methods compared are AlphaPruning (the proposed method), uniform layerwise sparsity, and OWL (a state-of-the-art non-uniform sparsity allocation method). Each of these methods is combined with three different intra-layer pruning techniques (Magnitude, Wanda, and SparseGPT) to thoroughly evaluate their effectiveness. Lower perplexity values indicate better model performance.

This table compares the performance of different heavy-tailed self-regularization (HT-SR) metrics for allocating layer-wise sparsity in large language models (LLMs). It shows that shape metrics, which capture the shape of the empirical spectral density (ESD) of weight matrices, generally outperform scale metrics (e.g., matrix norms) in determining layer importance for pruning. The best performing shape metric is PL_Alpha_Hill. The experiment uses LLaMA-7B model with 70% sparsity, and it is evaluated using WikiText perplexity and accuracy across seven zero-shot tasks.
This table compares the performance of different heavy-tailed self-regularization (HT-SR) metrics for allocating layer-wise sparsity in large language models (LLMs). It shows WikiText perplexity and average accuracy across seven zero-shot tasks when pruning a LLaMA-7B model to 70% sparsity using various metrics in conjunction with different intra-layer pruning methods. The results demonstrate that shape metrics generally outperform scale metrics, with PL_Alpha_Hill being the most effective.

This table presents the WikiText validation perplexity results for LLaMA and LLaMA-2 models after pruning to 70% sparsity using different methods. The table compares the performance of AlphaPruning against uniform sparsity and OWL (a state-of-the-art non-uniform sparsity allocation method) combined with three different intra-layer pruning techniques: Magnitude, Wanda, and SparseGPT. Lower perplexity values indicate better model performance after pruning.
Full paper#