TL;DR#
Private online learning, crucial for applications needing both accuracy and data protection, faces challenges in balancing privacy and regret (cumulative loss compared to the best model). Existing techniques struggle to attain optimal performance in high-privacy settings, often resulting in significantly increased regret. This necessitates improved algorithms.
This research introduces a novel transformation, termed L2P, that effectively translates lazy (low-switching) online learning algorithms into their differentially private counterparts. Applying L2P to existing lazy algorithms yields significantly improved regret bounds for both online prediction from experts and online convex optimization. These improved bounds are nearly optimal for a natural class of algorithms, showcasing the approach’s efficiency. The new transformation, therefore, offers a powerful tool for building state-of-the-art private online learning systems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and online learning. It presents a novel transformation improving the state-of-the-art regret bounds for differentially private online prediction from experts and online convex optimization, opening new avenues for future research in high-privacy regimes and providing a valuable tool for designing private algorithms. The tight lower bounds further enhance its significance by guiding future algorithm designs within the limited-switching framework. The work’s practical implications extend to various applications where privacy is paramount, such as personalized recommendations and healthcare.
Visual Insights#
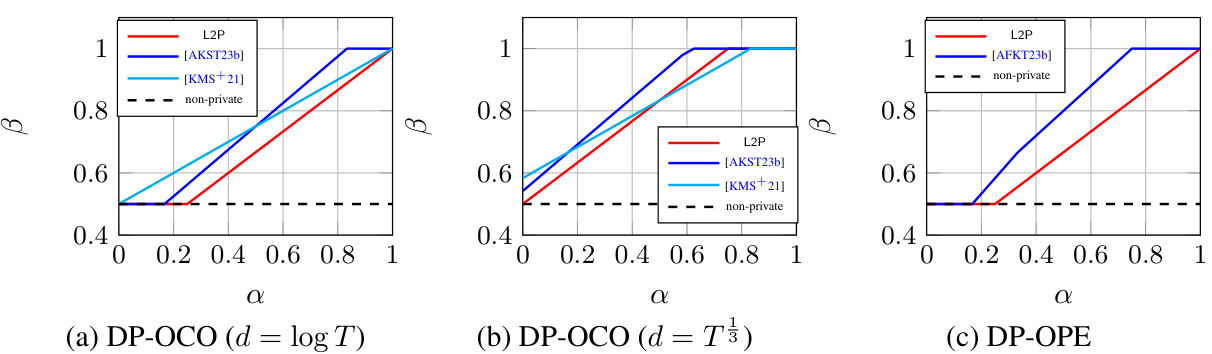
🔼 This figure compares the regret bounds of different differentially private online learning algorithms (L2P, [AKST23b], [KMS+21]) against the non-private regret bound. The x-axis represents the privacy parameter (ε = T-α), and the y-axis represents the exponent of the regret (Tβ). Each subplot shows the results for a specific problem (DP-OCO with different dimensionality d and DP-OPE). The figure illustrates how the proposed L2P algorithm achieves better regret bounds compared to the prior work in the high-privacy regime.
read the caption
Figure 1: Regret bounds for (a) DP-OCO with d = poly log(T), (b) DP-OCO with d = T1/3 and (c) DP-OPE with d = T. We denote the privacy parameter ε = T-α and regret Tβ, and plot β as a function of α (ignoring logarithmic factors).

🔼 This table compares the regret bounds achieved by prior work and the proposed work for differentially private online prediction from experts (DP-OPE) and differentially private online convex optimization (DP-OCO). The regret is a measure of the algorithm’s performance compared to the best possible outcome in hindsight. The table shows that the new algorithms significantly improve upon the state-of-the-art, especially in the high-privacy regime where ε is small.
read the caption
Table 1: Regret for approximate (ε, δ)-DP algorithms. For readability, we omit logarithmic factors that depend on T and 1/δ.
Full paper#



















