TL;DR#
Prior-data fitted networks (PFNs) offer a promising approach to tabular classification, leveraging in-context learning for strong performance. However, current PFNs struggle with large datasets, limiting their applicability. Existing scaling methods like sketching and fine-tuning proved inadequate, failing to achieve comparable accuracy to traditional methods like boosted trees.
TuneTables tackles this limitation by introducing a novel prompt-tuning strategy. It compresses large datasets into smaller, learned contexts, significantly enhancing PFN scalability and performance. Extensive experiments demonstrate TuneTables’ superior performance across various datasets, outperforming other algorithms while optimizing fewer parameters and improving inference speed. Furthermore, it showcases potential as an interpretability tool and for bias mitigation.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with tabular data because it presents TuneTables, a novel method that significantly improves the performance of prior-data fitted networks (PFNs) on large datasets. This addresses a key limitation of existing PFNs and opens new avenues for research in parameter-efficient fine-tuning and context optimization strategies, particularly relevant in the context of growing interest in parameter-efficient and bias-mitigating approaches in machine learning.
Visual Insights#

🔼 This figure illustrates the TuneTables method, a novel prompt-tuning technique for prior-data fitted networks (PFNs). It compares TuneTables to the original TabPFN approach, highlighting key differences and advantages. TuneTables uses prompt tuning on a pre-trained TabPFN to create compact, learned embeddings representing large datasets. This leads to improved performance and faster inference times. The figure also showcases TuneTables’ additional capabilities in bias mitigation and interpretability.
read the caption
Figure 1: TuneTables: a novel prompt-tuning technique for prior-data fitted networks. TuneTables performs prompt tuning on a pre-trained prior-fitted network (TabPFN) to distill real-world datasets into learned embeddings, allowing for stronger performance and faster inference time than TabPFN in many cases. TuneTables also expands the capabilities of pre-trained PFNs; by way of example, we demonstrate its effectiveness for bias mitigation, and as an interpretability tool.

🔼 This table presents a comparison of TuneTables against 19 other state-of-the-art algorithms for tabular classification on 98 datasets. The metrics used for comparison include mean accuracy, mean rank (based on accuracy), mean Z-score (normalized accuracy across datasets), standard deviation of Z-scores, median Z-score, and number of wins (datasets where the algorithm outperformed others). The table highlights TuneTables’ strong performance, achieving the highest mean rank and a significant number of wins.
read the caption
Table 1: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm's normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.
In-depth insights#
TuneTables: Overview#
TuneTables offers a novel approach to optimizing prior-data fitted networks (PFNs) for tabular classification. It addresses the scalability limitations of existing PFNs like TabPFN, significantly improving performance on large datasets. The core innovation is a parameter-efficient fine-tuning strategy, prompt tuning, that compresses large datasets into a smaller learned context. This allows TuneTables to achieve competitive accuracy with significantly faster inference times compared to traditional methods. Furthermore, the learned context can be leveraged for interpretability and bias mitigation, enhancing the practical utility of PFNs. The approach is evaluated extensively, demonstrating state-of-the-art results across numerous datasets and algorithms. The open-sourcing of the code and results is a significant contribution, enabling broad adoption and further research.
Prompt Tuning PFNs#
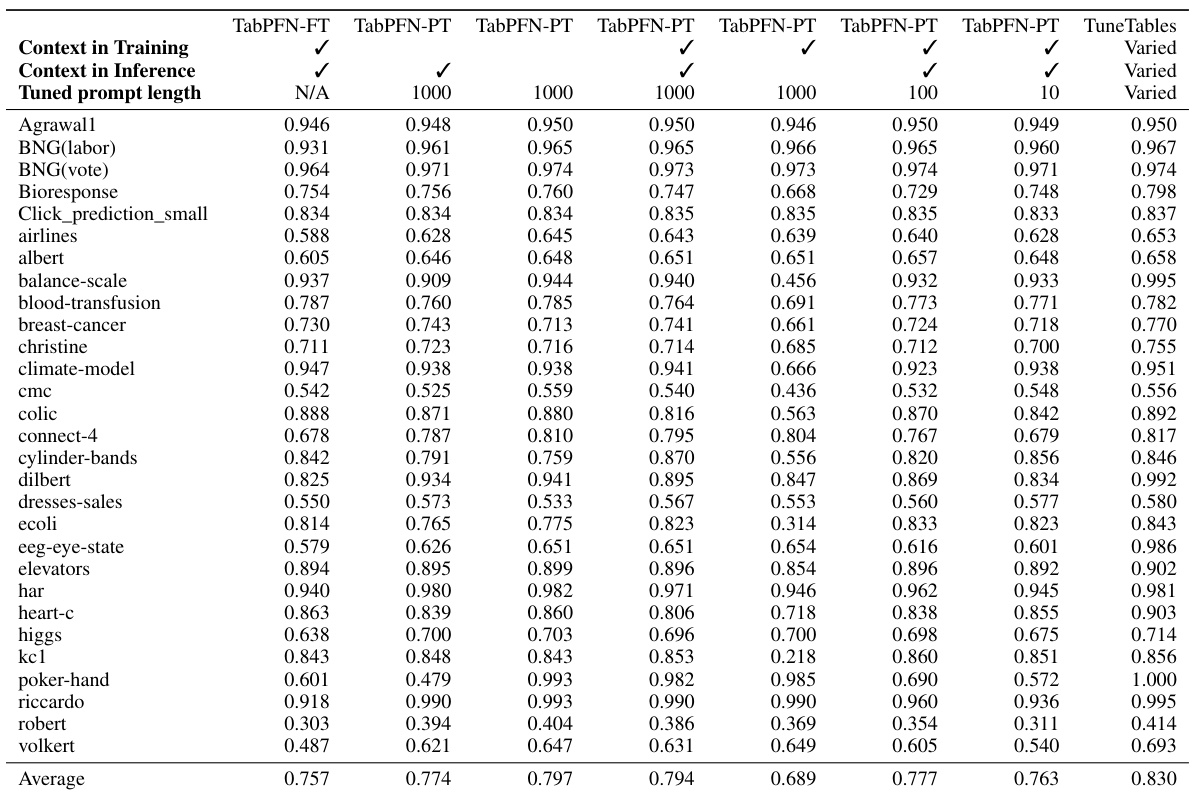
Prompt tuning, a technique borrowed from large language models (LLMs), offers a novel approach to enhance Prior-Data Fitted Networks (PFNs). Instead of extensive retraining, prompt tuning modifies the input embeddings of a pre-trained PFN, effectively creating a learned context that adapts the network to new tasks. This approach is particularly attractive for PFNs due to their inherent reliance on in-context learning. By tuning a smaller set of parameters, prompt tuning achieves parameter-efficiency, allowing for quicker adaptation and potentially mitigating overfitting. The effectiveness of prompt tuning on PFNs is an open research area requiring careful exploration of prompt designs, tuning methods, and their impact on model performance and generalization. Furthermore, combining prompt tuning with techniques like sketching and feature selection could yield scalable solutions for large tabular datasets, where PFNs traditionally face limitations.
Bias Mitigation#
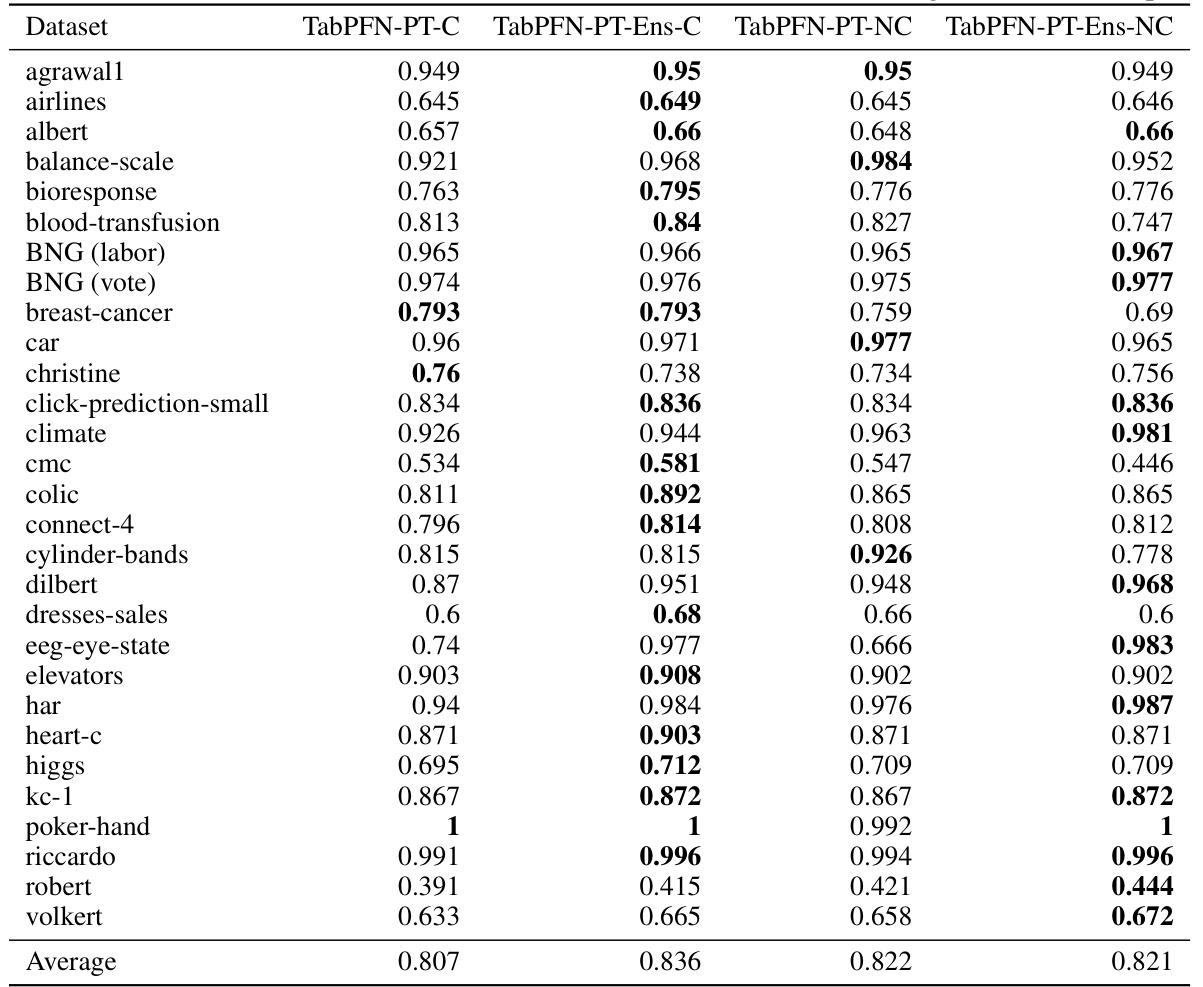
The section on Bias Mitigation in this research paper explores a novel approach to address algorithmic bias in tabular classification. The core idea is to leverage prompt tuning within a pre-trained prior-data fitted network (PFN) to learn a compressed representation of the data. This distilled representation, acting as a learned context, is then utilized during inference to generate predictions. The strategy directly addresses the limitations of existing PFNs, which struggle with large datasets. The methodology allows for multi-objective optimization, meaning the system can be fine-tuned not only to enhance accuracy but simultaneously to mitigate biases by optimizing fairness objectives (e.g., demographic parity). This innovative approach presents a parameter-efficient technique, modifying only a small subset of the original model parameters and allowing for potentially faster inference times. The method’s effectiveness is demonstrated empirically, suggesting TuneTables, as the method is called, can serve as both a high-performing classifier and a valuable tool for improving fairness and interpretability in PFNs.
Scalability Methods#
Addressing scalability in machine learning models, particularly for tabular data, is crucial. This involves tackling challenges related to computational resources, memory limitations, and the size of datasets. Effective scalability methods often employ techniques such as data subsampling, which involves selecting a representative subset of the data for training and inference; feature selection, focusing on a smaller set of the most relevant features; and parameter-efficient fine-tuning, which optimizes a minimal subset of parameters in a pre-trained model, instead of training from scratch. Context optimization strategies, which involve compressing large datasets into smaller learned contexts, offer significant improvements. The choice of scalability method depends on the specific problem and model, requiring careful consideration of trade-offs between accuracy, computational cost, and memory usage. Hybrid approaches, combining multiple techniques, may yield the best results.
Future Research#
The authors suggest several promising avenues for future research. Parameter-efficient fine-tuning, using techniques like LoRA or QLoRA, could significantly improve PFNs by reducing the number of parameters updated during fine-tuning, thereby enhancing efficiency and scalability. Furthermore, exploring sparse mixture-of-experts PFNs leveraging router networks, inspired by advancements in LLMs, is proposed to improve model performance and efficiency. Extending TuneTables to handle more complex data modalities and applying the prompt-tuning framework to other machine learning tasks are additional exciting prospects. A deeper investigation into bias mitigation strategies, going beyond demographic parity, is crucial, particularly to explore the subtle interactions between fairness and accuracy. Lastly, the authors advocate for developing more sophisticated techniques for evaluating and comparing model performance in large-scale tabular datasets given the computational cost of these evaluations.
More visual insights#
More on figures

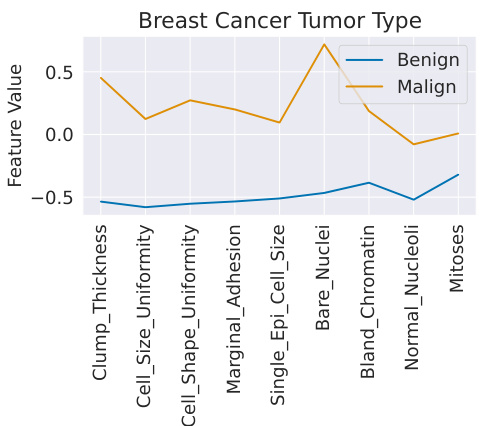
🔼 This figure shows a critical difference plot comparing TuneTables to 18 other state-of-the-art tabular classification algorithms across 98 datasets. The algorithms are ranked by their average accuracy rank. Algorithms with statistically insignificant differences in performance are connected by a horizontal line. TuneTables achieves the highest average rank, indicating superior overall performance.
read the caption
Figure 2: TuneTables and state-of-the-art tabular models. A critical difference plot according to mean accuracy rank across the 98 datasets in Table 1 of [51]. Algorithms which are not significantly different (p > 0.05) are connected with a horizontal black bar. TuneTables achieves the highest mean rank of any algorithm.

🔼 This figure compares the performance of TuneTables, CatBoost, and TabPFNs3000 across datasets with varying sizes and number of features. The left panel shows that TabPFNs3000, while strong on smaller datasets, underperforms CatBoost on larger ones. The middle and right panels demonstrate that TuneTables consistently outperforms TabPFNs3000 across the datasets and is competitive with CatBoost, addressing the scalability limitations of TabPFNs3000.
read the caption
Figure 3: TuneTables addresses TabPFN's limitations. (Left) Motivating example (using the subset of [51]on which both CatBoost and TabPFNs3000 report results): TabPFNs3000 is best on small datasets, but when scaled past 3000 datapoints and 100 features, TabPFNs3000 significantly underperforms. (Middle) CatBoost vs. TuneTables on LARGESCALETABLES: By contrast, TuneTables is competitive with CatBoost on all datasets, mitigating the limitations of TabPFN. (Right) TabPFNs3000 vs. TuneTables on LARGESCALETABLES : TuneTables outperforms TabPFNs3000 on datasets with a high number of datapoints or features. The colorbar on the y axis represents the comparative change in per-dataset accuracy between two algorithms (A: blue, B: red). Positive numbers represent the absolute gain in accuracy of B w.r.t. A, negative numbers represent the absolute gain in accuracy of A w.r.t. BΒ.
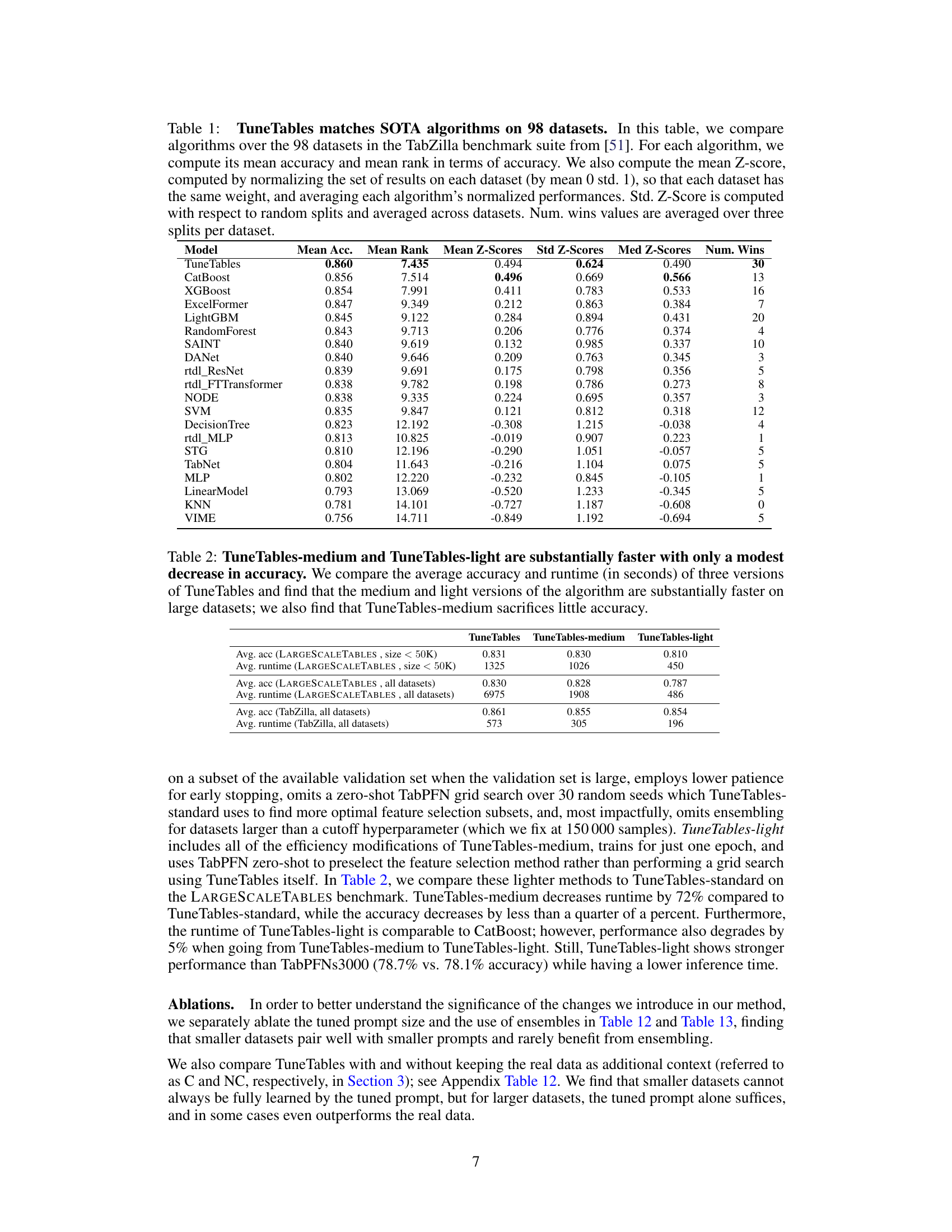
🔼 This figure shows a two-example prompt dataset for the breast cancer dataset. The two examples, one benign and one malignant, are used as a minimal context for the TabPFN model. The plot visually demonstrates that the malignant example has higher values for all features compared to the benign example, suggesting that high feature values are associated with malignancy. This highlights TuneTables’ ability to extract discriminative features even from a tiny dataset.
read the caption
Figure 4: Dataset with high accuracies from just two datapoints. Shown is a two-example prompt dataset for the breast cancer dataset [78]. Malign class example has higher values for all features than benign class.

🔼 This figure shows a critical difference plot comparing the performance of TuneTables against 18 other state-of-the-art tabular classification algorithms across 98 datasets. The algorithms are ranked by their mean accuracy rank. Algorithms with statistically insignificant differences in performance are connected by horizontal bars. The plot highlights TuneTables’ superior average performance compared to the other algorithms.
read the caption
Figure 2: TuneTables and state-of-the-art tabular models. A critical difference plot according to mean accuracy rank across the 98 datasets in Table 1 of [51]. Algorithms which are not significantly different (p > 0.05) are connected with a horizontal black bar. TuneTables achieves the highest mean rank of any algorithm.
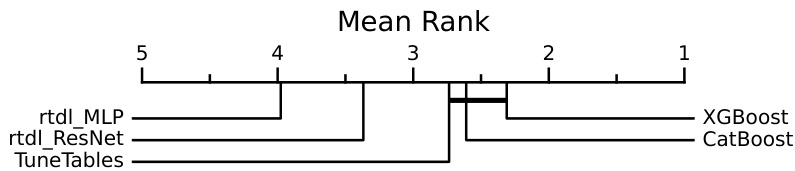
🔼 This figure compares the performance of TuneTables against other state-of-the-art tabular classification models across 98 datasets using a critical difference plot. The plot visually shows the mean accuracy rank of each algorithm, indicating TuneTables’ superior performance in achieving the highest average rank compared to its competitors. Algorithms with statistically insignificant differences in performance are linked by horizontal bars.
read the caption
Figure 2: TuneTables and state-of-the-art tabular models. A critical difference plot according to mean accuracy rank across the 98 datasets in Table 1 of [51]. Algorithms which are not significantly different (p > 0.05) are connected with a horizontal black bar. TuneTables achieves the highest mean rank of any algorithm.
🔼 This figure shows a critical difference plot comparing TuneTables to other state-of-the-art tabular classification models across 98 datasets. The plot displays the mean accuracy rank of each algorithm, with statistically insignificant differences (p > 0.05) indicated by horizontal bars connecting the algorithms. TuneTables is shown to have the highest average ranking, demonstrating superior performance compared to other methods.
read the caption
Figure 2: TuneTables and state-of-the-art tabular models. A critical difference plot according to mean accuracy rank across the 98 datasets in Table 1 of [51]. Algorithms which are not significantly different (p > 0.05) are connected with a horizontal black bar. TuneTables achieves the highest mean rank of any algorithm.

🔼 This figure illustrates the TuneTables method, which enhances prior-data fitted networks (PFNs) by using prompt tuning. It shows how TuneTables improves performance and speed compared to the original TabPFN. The image also highlights additional benefits of the technique such as bias mitigation and interpretability.
read the caption
Figure 1: TuneTables: a novel prompt-tuning technique for prior-data fitted networks. TuneTables performs prompt tuning on a pre-trained prior-fitted network (TabPFN) to distill real-world datasets into learned embeddings, allowing for stronger performance and faster inference time than TabPFN in many cases. TuneTables also expands the capabilities of pre-trained PFNs; by way of example, we demonstrate its effectiveness for bias mitigation, and as an interpretability tool.
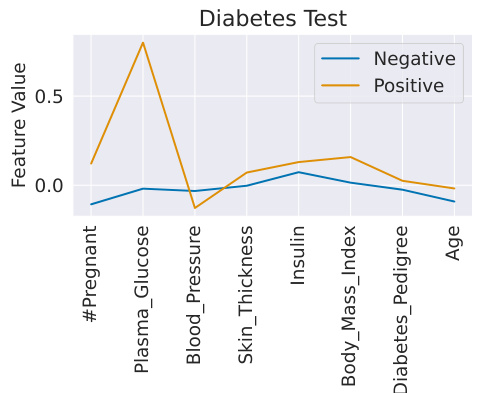
🔼 This figure shows a two-example prompt dataset for the breast cancer dataset. It demonstrates that TuneTables can achieve high accuracy using just two datapoints as context, effectively summarizing the dataset’s key discriminative features. Notably, the malign class example exhibits higher values across all features compared to the benign class, highlighting the importance of these features for classification.
read the caption
Figure 4: Dataset with high accuracies from just two datapoints. Shown is a two-example prompt dataset for the breast cancer dataset [78]. Malign class example has higher values for all features than benign class.
More on tables

🔼 This table presents a comparison of TuneTables against 19 other state-of-the-art algorithms on 98 tabular datasets. It shows the mean accuracy, mean rank, mean Z-score (normalized accuracy), standard deviation of Z-scores, median Z-score, and the number of times each algorithm achieved the highest accuracy across the datasets. The results highlight TuneTables’ superior performance.
read the caption
Table 2: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm's normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.

🔼 This table presents the results of multi-objective optimization experiments using prompt tuning to mitigate predictive bias. It compares the performance of TabPFN and TuneTables across four datasets (Adult, Speeddating, Compas, NLSY) in terms of accuracy (Acc) and demographic parity (DP). Two TuneTables variations are shown: one optimized for accuracy alone and another optimized for both accuracy and demographic parity. The results show that TuneTables generally improves over TabPFN in terms of both accuracy and fairness.
read the caption
Table 3: TuneTables significantly improves accuracy and demographic parity. In these multi-objective optimization experiments, we consider prompt tuning for mitigating predictive bias, comparing TabPFN to TuneTables, tuning for accuracy alone vs. accuracy and demographic parity. TuneTables improves over TabPFN with respect to both objectives.

🔼 This table compares TuneTables to 19 other state-of-the-art tabular classification algorithms on 98 datasets. The metrics used for comparison include mean accuracy, mean rank, mean z-score (a normalized measure of accuracy across all datasets), standard deviation of z-scores, median z-score, and the number of times each algorithm achieved the highest accuracy (wins). The results show TuneTables outperforms the other algorithms on average across all datasets.
read the caption
Table 1: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm’s normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.

🔼 This table presents the hyperparameter settings used for TuneTables and TabPFNs3000 across different dataset sizes. It shows how certain hyperparameters like batch size, real data quantity, ensemble size, and tuned prompt dimensions are adjusted depending on whether the dataset has less than or more than 2000 samples. The table also details the epoch numbers, warmup strategies, sequence length per batch, early stopping criteria, learning rates, validation frequencies, maximum validation set sizes during training, optimizers used, loss functions, and the methods for selecting tuned prompt labels.
read the caption
Table 5: TuneTables and TabPFNs3000 hyperparameter configurations based on number of samples.
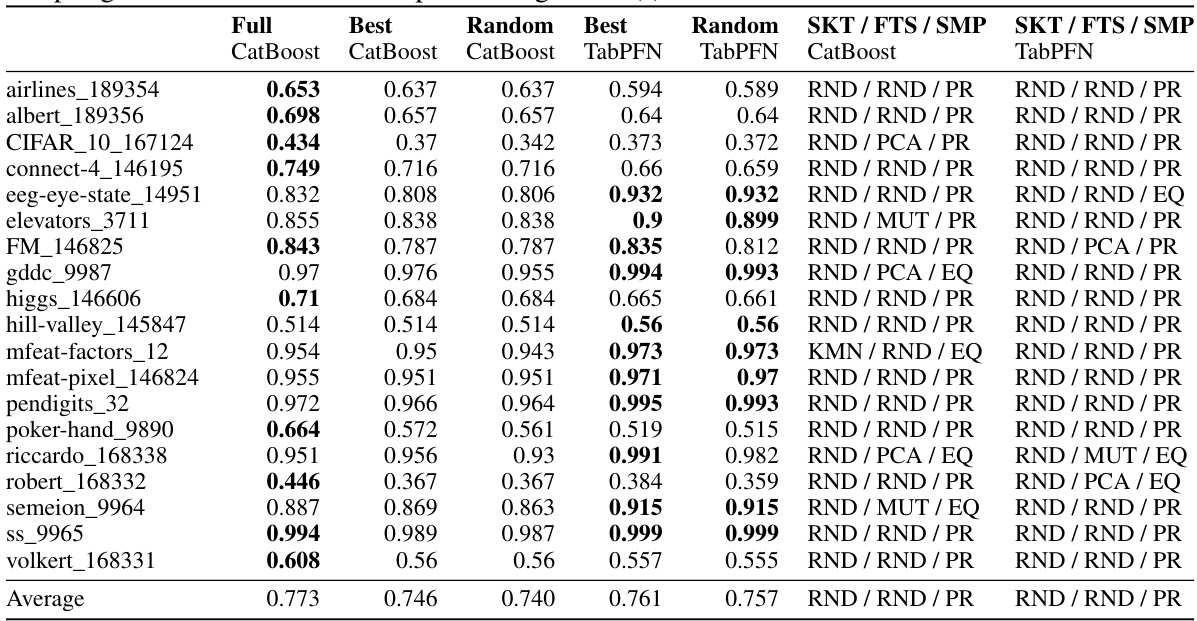
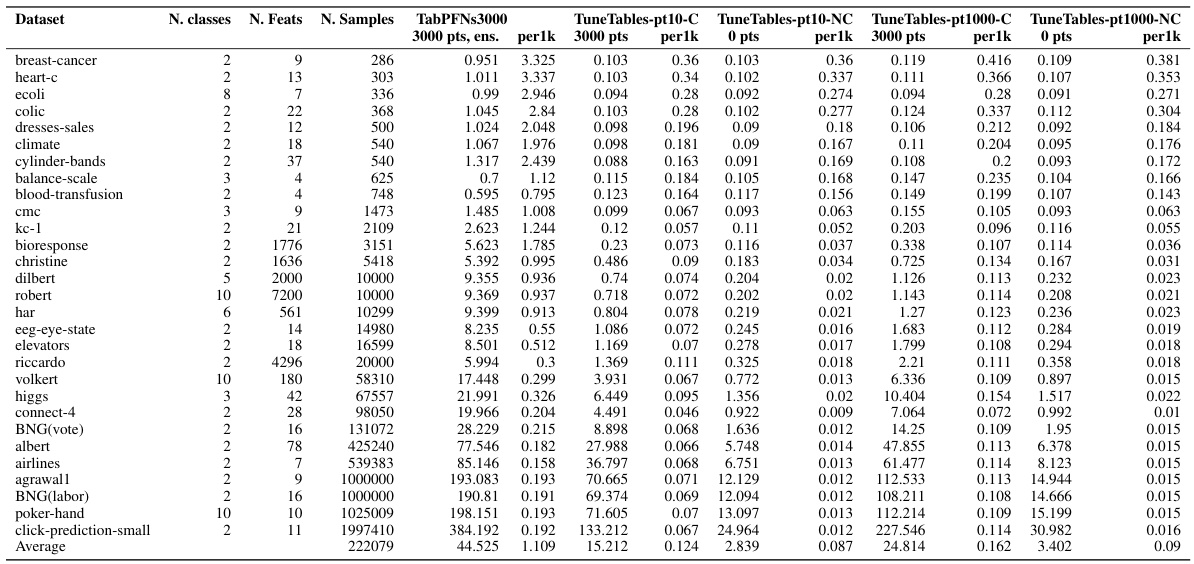
🔼 This table compares the performance of TabPFN and CatBoost on a subset of datasets from [51], focusing on those with many features or samples. It investigates the impact of different sketching (subsampling), feature selection, and sampling strategies on both models’ accuracy. The results show that random sampling often suffices, while PCA and mutual information improve feature selection performance when many features are present. The table highlights the best methods for each strategy and indicates the best-performing model for each dataset.
read the caption
Table 6: Comparative performance of TabPFN and CatBoost with sketching, feature selection, and sampling methods. On a distinct subset of the datasets in [51] selected to emphasize datasets with many features or many samples, we compare CatBoost and TabPFNs3000. When both models are limited to 3000 samples, TabPFNs3000 performs better on 12 of 17 datasets where significant differences exist. When CatBoost is allowed access to the entire training data, the win rate is identical. In most cases, random sample selection is sufficient for optimal performance. Both models benefit from PCA and mutual information dimension reduction when the feature space is large. The columns labeled SKT / FTS / SMP list the best performing method for sketching, feature subsampling and label-aware sketching technique, respectively. Label-aware sketching refers to a strategy where we either sample instances proportionate to their labels, or we oversample minority classes with replacement to create a class-balanced distribution. While the choice of label-aware sketching strategy is often impactful (and we use it in TuneTables), and the choice of feature subselection method can be important for some datasets, in all but one case, no sketching method we test outperforms random sampling. Bold indicates the best-performing model(s).
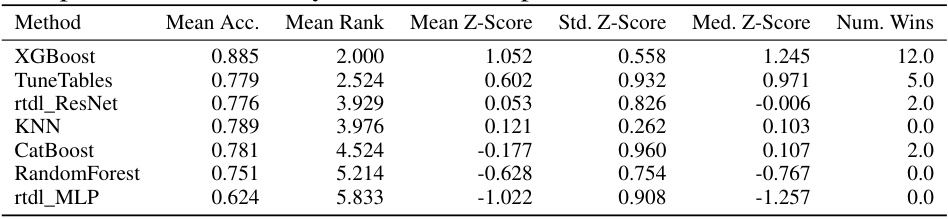
🔼 This table compares the performance of TuneTables and other algorithms on datasets with a large number of classes. It shows that TuneTables outperforms other algorithms in terms of mean accuracy, mean rank, mean Z-score, and number of wins, demonstrating its effectiveness in handling datasets with more classes than those used during its pretraining.
read the caption
Table 7: Comparison of algorithms on datasets with a large number of classes. TuneTables can effectively handle datasets with more classes than the ones used for pretraining, which was not possible with TabPFN. For each algorithm, we compute its mean test accuracy, and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm's normalized performances. We see that TuneTables performs the best across all performance-oriented metrics. Fractional num. wins values are averaged over three splits per dataset, and reflect the presence of multi-way ties on certain splits.
🔼 This table presents a comparison of TuneTables’ performance against 19 other state-of-the-art algorithms on a benchmark suite of 98 tabular datasets. The comparison uses several metrics: mean accuracy, mean rank, mean Z-score (normalized accuracy across datasets), standard deviation of Z-scores, median Z-score, and the number of times each algorithm achieved the best accuracy on a dataset. This provides a comprehensive overview of TuneTables’ performance relative to existing methods on a diverse set of tabular classification problems.
read the caption
Table 1: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm's normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.

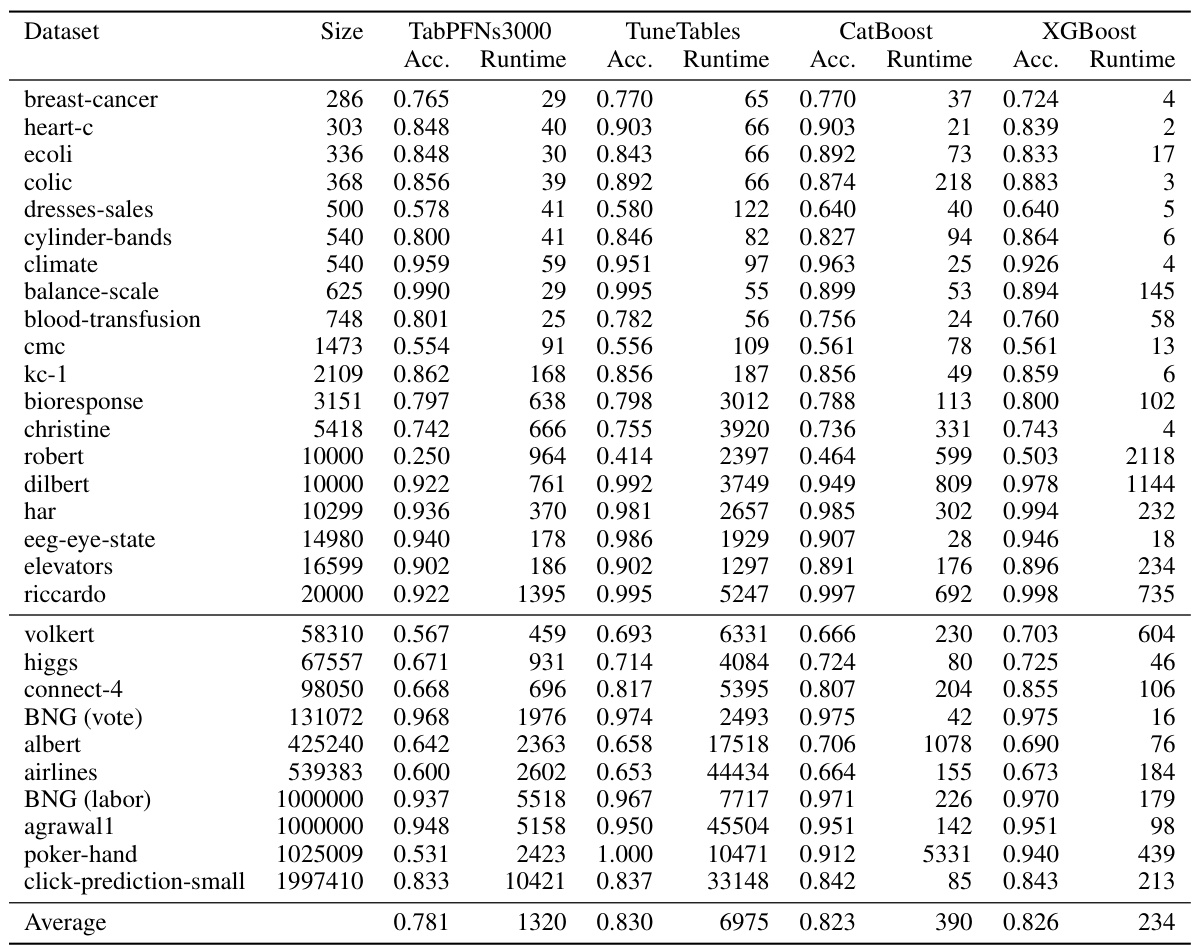
🔼 This table compares TuneTables against four other neural network models on a subset of the LARGESCALETABLES benchmark. It shows mean accuracy, median accuracy, mean rank, median rank, mean Z-score, median Z-score, and the number of wins for each model. The Z-score is a normalized metric that accounts for dataset variations. TuneTables demonstrates the highest performance across most metrics.
read the caption
Table 9: Comparison of neural nets on LARGESCALETABLES. We compare TuneTables to other prominent deep learning methods for tabular data on the 17 datasets in LARGESCALETABLES for which all algorithms reported results. For each algorithm, we compute its different metrics of accuracy and rank. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm’s normalized performances. We see that TuneTables performs the best across all performance-oriented metrics. Fractional num. wins values are averaged over three splits per dataset, and reflect the presence of multi-way ties on certain splits.
🔼 This table presents a comparison of TuneTables’ performance against 19 other state-of-the-art algorithms across 98 datasets from the TabZilla benchmark. The table shows mean accuracy, rank (lower is better), mean and standard Z-scores (across datasets), and the number of wins for each algorithm across all datasets. Z-scores are used to account for variance in dataset difficulty. The results demonstrate TuneTables’ superior performance in terms of average accuracy and the number of datasets where it outperforms other methods.
read the caption
Table 1: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm's normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.

🔼 This table compares TuneTables to 19 other algorithms (including three GBDTs and 11 neural networks) on 98 datasets from the TabZilla benchmark. The table shows mean accuracy, mean rank, Z-scores (both mean and standard deviation), median Z-score, and the number of wins for each algorithm. The results demonstrate TuneTables’s performance compared to state-of-the-art algorithms.
read the caption
Table 1: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm's normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.
🔼 This table compares the performance of TabPFN and CatBoost on a subset of datasets from the TabZilla benchmark, focusing on datasets with many features or samples. It investigates the impact of different sketching (subsampling), feature selection, and sampling methods on both models’ accuracy. The results show that random sampling is often sufficient, while PCA and mutual information feature selection improve performance when dealing with high-dimensional data. The table highlights the best-performing methods for each combination of techniques.
read the caption
Table 6: Comparative performance of TabPFN and CatBoost with sketching, feature selection, and sampling methods. On a distinct subset of the datasets in [51] selected to emphasize datasets with many features or many samples, we compare CatBoost and TabPFNs3000. When both models are limited to 3000 samples, TabPFNs3000 performs better on 12 of 17 datasets where significant differences exist. When CatBoost is allowed access to the entire training data, the win rate is identical. In most cases, random sample selection is sufficient for optimal performance. Both models benefit from PCA and mutual information dimension reduction when the feature space is large. The columns labeled SKT / FTS / SMP list the best performing method for sketching, feature subsampling and label-aware sketching technique, respectively. Label-aware sketching refers to a strategy where we either sample instances proportionate to their labels, or we oversample minority classes with replacement to create a class-balanced distribution. While the choice of label-aware sketching strategy is often impactful (and we use it in TuneTables), and the choice of feature subselection method can be important for some datasets, in all but one case, no sketching method we test outperforms random sampling. Bold indicates the best-performing model(s).
🔼 This table presents a comparison of TuneTables’ performance against 19 other state-of-the-art algorithms on 98 tabular datasets. The metrics used for comparison include mean accuracy, mean rank, mean Z-score, standard deviation of Z-scores, median Z-score, and the number of times each algorithm achieved the best performance. The Z-score normalization helps to account for variations in dataset difficulty. This allows for a more fair comparison of algorithm performance across different types of tabular data.
read the caption
Table 1: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm's normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.
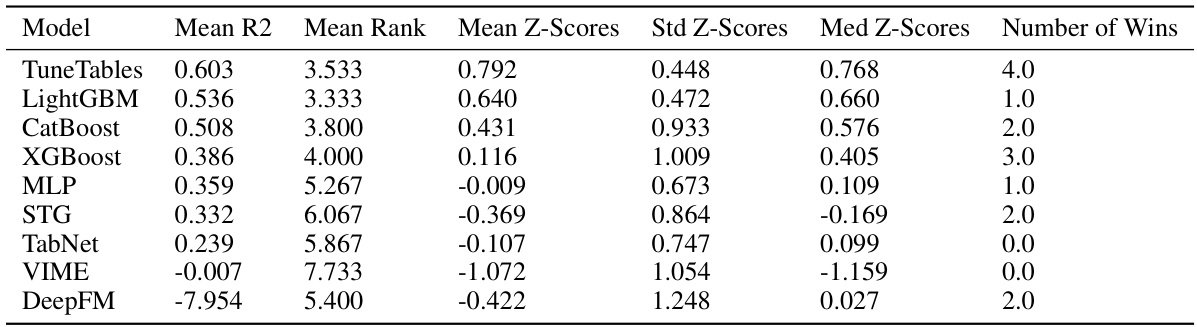
🔼 This table presents a comparison of TuneTables’ performance against 19 other state-of-the-art algorithms on 98 tabular datasets from the TabZilla benchmark. The comparison uses multiple metrics including mean accuracy, mean rank (based on accuracy), mean Z-score (a normalized accuracy score), standard deviation of the Z-score, median Z-score, and the number of times each algorithm achieved the best accuracy. This provides a comprehensive overview of TuneTables’ performance relative to other methods.
read the caption
Table 1: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm's normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.

🔼 This table compares the performance of TuneTables against other state-of-the-art algorithms on 19 datasets from the LARGESCALETABLES benchmark with a maximum of 50,000 samples. It provides a comprehensive performance comparison using several metrics including mean accuracy, runtime, rank, Z-score (both mean and standard deviation), and the number of wins. The Z-score normalization helps to account for variations in dataset difficulty by ensuring each dataset has the same weight in the overall score.
read the caption
Table 15: TuneTables matches SOTA algorithms on small and medium-sized datasets. In this table, we compare algorithms over 19 datasets in LARGESCALETABLES with at most 50 000 samples. For each algorithm, we compute its mean accuracy, mean runtime, and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm’s normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Fractional num. wins values are averaged over three splits per dataset, and reflect the presence of multi-way ties on certain splits. This table is similar to Table 1, but the benchmark is LARGESCALETABLES, and the search spaces for XGBoost and CatBoost are expanded to include more trees.

🔼 This table presents a comparison of TuneTables against 19 other state-of-the-art algorithms on 98 tabular datasets from the TabZilla benchmark. It shows the mean accuracy, mean rank (lower is better), mean Z-score (normalized performance across datasets), standard deviation of Z-scores, median Z-score and the number of times each algorithm achieved the best accuracy across the datasets. This allows for a comprehensive comparison of performance, accounting for dataset variations and providing a statistical measure of significance.
read the caption
Table 1: TuneTables matches SOTA algorithms on 98 datasets. In this table, we compare algorithms over the 98 datasets in the TabZilla benchmark suite from [51]. For each algorithm, we compute its mean accuracy and mean rank in terms of accuracy. We also compute the mean Z-score, computed by normalizing the set of results on each dataset (by mean 0 std. 1), so that each dataset has the same weight, and averaging each algorithm’s normalized performances. Std. Z-Score is computed with respect to random splits and averaged across datasets. Num. wins values are averaged over three splits per dataset.
Full paper#