TL;DR#
Adaptive Risk Control (ARC) is a valuable tool for reliable online decision-making, but it can distribute reliability unevenly across different data subpopulations, potentially causing unfair outcomes. This paper addresses this limitation by introducing Localized Adaptive Risk Control (L-ARC), which focuses on achieving statistical risk guarantees that are localized to specific subpopulations.
L-ARC updates a threshold function within a reproducing kernel Hilbert space, where the kernel determines the level of localization. The theoretical analysis demonstrates a trade-off between localization of risk guarantees and convergence speed. Empirical results from various applications showcase L-ARC’s effectiveness in producing prediction sets with improved fairness and reliability across different subpopulations.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel online calibration scheme that improves the fairness and reliability of predictive models. It addresses the limitations of existing methods by providing localized statistical risk control guarantees, which are crucial for high-stakes applications where fairness across diverse subgroups is essential. This work opens up new avenues for research in online calibration and reliable decision-making across various domains.
Visual Insights#

🔼 This figure shows the calibration of a tumor segmentation model using both ARC and L-ARC methods. Two datasets (Kvasir and Larib) are used, and L-ARC demonstrates superior performance across both, unlike ARC which favors one dataset over the other.
read the caption
Figure 1: Calibration of a tumor segmentation model via ARC [Angelopoulos et al., 2024a] and the proposed localized ARC, L-ARC. Calibration data comprises images from multiple sources, namely, the Kvasir data set [Jha et al., 2020] and the ETIS-LaribPolypDB data set [Silva et al., 2014]. Both ARC and L-ARC achieve worst-case deterministic long-term risk control in terms of false negative rate (FNR). However, ARC does so by prioritizing Kvasir samples at the detriment of the Larib data source, for which the model has poor FNR performance. In contrast, L-ARC can yield uniformly satisfactory performance for both data subpopulations.
In-depth insights#
Localized Risk#
The concept of “Localized Risk” in the context of adaptive risk control signifies a significant departure from traditional methods. Instead of focusing on overall risk reduction, it emphasizes achieving risk control within specific subpopulations or regions of the input space. This is particularly crucial in scenarios where fairness and equitable performance across diverse groups are paramount. By tailoring risk management to particular segments, the approach addresses the potential for unfairness inherent in some global risk minimization strategies. For example, in medical imaging, localized risk control can ensure that a model performs well in identifying tumors across various patient demographic groups, not just those who are most represented in the dataset. The key innovation lies in its ability to localize guarantees in the input space, allowing the model to adapt more effectively to heterogeneity and offer enhanced risk control. This necessitates careful consideration of the choice of weighting functions and kernel functions, which dictate the degree of localization and ultimately the trade-off between localized guarantees and convergence speed. The theoretical analysis likely explores the trade-offs involved and provides guarantees on the long-term and localized statistical risk control performance.
L-ARC Algorithm#
The L-ARC algorithm presents a novel approach to online calibration, enhancing the fairness and reliability of prediction sets. Unlike traditional ARC, which uses a single scalar threshold, L-ARC employs a threshold function updated within a reproducing kernel Hilbert space (RKHS). This allows for localized risk control, addressing the uneven distribution of risk guarantees across different subpopulations that can occur with ARC. The choice of RKHS kernel dictates the degree of localization and affects the trade-off between the speed of convergence to the target risk and the precision of localized risk guarantees. Theoretical guarantees demonstrate the convergence of the cumulative risk to a neighborhood of the target loss level and provide asymptotic localized statistical risk guarantees. The algorithm demonstrates efficacy in tasks such as image segmentation, electricity demand forecasting, and beam selection, showcasing its adaptability and improved performance over standard ARC in addressing conditional risk control. A key challenge is the increase in memory requirements due to the online adaptation of the threshold function within the RKHS; however, the paper also explores memory-efficient variants of the algorithm.
Empirical Tests#
A robust empirical testing section would systematically evaluate the proposed Localized Adaptive Risk Control (L-ARC) algorithm. It should begin by clearly defining the metrics used to assess performance, such as long-term risk, marginal coverage, and conditional coverage across various subgroups. The experiments should involve diverse datasets and tasks to demonstrate the generalizability of L-ARC. Comparisons with existing methods, like standard ARC and potentially other online calibration techniques, are crucial to highlight L-ARC’s improvements. Furthermore, the analysis should explore the impact of key hyperparameters on L-ARC’s performance and provide visualizations such as graphs and tables that clearly illustrate the results. A discussion on the statistical significance of the findings is also essential for a convincing evaluation. Finally, an examination of the algorithm’s computational efficiency and scalability is important, along with any challenges encountered during implementation. Overall, a thorough empirical evaluation section strengthens the paper significantly.
Future Work#
The paper on Localized Adaptive Risk Control (L-ARC) concludes by suggesting several avenues for future research. A key area is improving the memory efficiency of L-ARC, which currently scales linearly with the number of data points. Addressing this limitation, perhaps through techniques like online kernel approximations or selective memory updating, is crucial for practical applications involving large datasets. Another important direction is exploring different kernel functions and their impact on localization and convergence speed. A more comprehensive theoretical analysis of the trade-offs between localization level and other performance metrics is warranted. Furthermore, investigating the applicability of L-ARC beyond the specific tasks demonstrated (electricity demand forecasting, tumor segmentation, beam selection) would strengthen its impact. Extending L-ARC to handle non-i.i.d data or more complex forms of feedback would further enhance its robustness and adaptability to real-world scenarios. Finally, a deeper study into the impact of hyperparameter tuning on L-ARC’s performance, particularly regarding the regularization parameter and learning rate, could optimize its practical effectiveness.
Memory Limits#
The concept of ‘Memory Limits’ in the context of online machine learning algorithms, particularly those focused on adaptive risk control, is critical. The core challenge is balancing the need for accurate, localized risk control with the computational constraints imposed by limited memory. Algorithms like Localized Adaptive Risk Control (L-ARC) update a threshold function within a Reproducing Kernel Hilbert Space (RKHS). However, maintaining the entire history of past observations and associated model parameters necessitates ever-increasing memory. This poses a scalability problem, as the model’s size grows linearly with the number of time steps. Strategies for mitigating memory limits include approximation techniques where the model’s memory footprint is kept under control. This might involve truncating the history of observations used to update the model, leading to a trade-off between accuracy and memory efficiency. The optimal approach would involve carefully balancing the memory constraints with the performance metrics of the algorithm. Investigating alternative data structures, or model compression techniques could potentially improve scalability, but may also compromise the desired level of localized risk control accuracy.
More visual insights#
More on figures
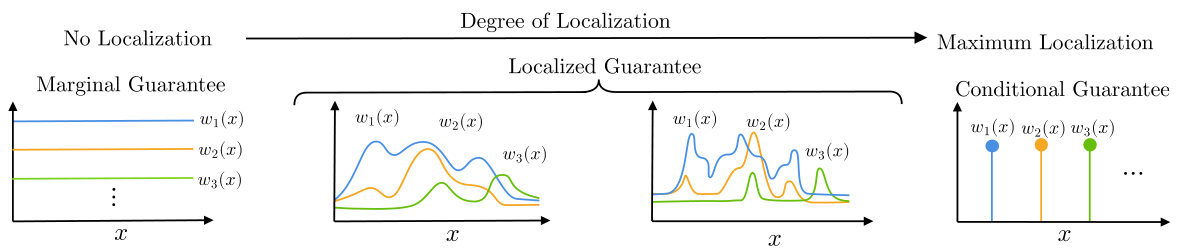
🔼 This figure illustrates the concept of localized guarantees in L-ARC. The x-axis represents the input space (covariates X). Different panels show how the choice of reweighting function influences the level of localization in the statistical risk guarantee. The leftmost panel shows constant reweighting functions (no localization), resulting in a marginal guarantee. The rightmost panel shows maximally localized reweighting functions (Dirac delta functions), achieving a conditional guarantee. The middle panel shows intermediate levels of localization.
read the caption
Figure 2: The degree of localization in L-ARC is dictated by the choice of the reweighting function class W via the marginal-to-conditional guarantee (9). At the leftmost extreme, we illustrate constant reweighting functions, for which marginal guarantees are recovered. At the rightmost extreme, reweighting with maximal localization given by Dirac delta functions for which the criterion (9) corresponds to a conditional guarantee. In between the two extremes lie function sets W with an intermediate level of localization yielding localized guarantees.

🔼 The figure displays the long-term coverage and average miscoverage error for ARC and L-ARC algorithms on the Elec2 dataset. The left panel shows the long-term coverage for ARC and L-ARC with different values of localization parameter ’l’. The right panel shows the average miscoverage error, broken down by day of the week (weekdays vs weekends) and marginalized over all days. It illustrates the impact of the localization parameter on the algorithm’s performance.
read the caption
Figure 3: Long-term coverage (left) and average miscoverage error (right), marginalized and conditioned on weekdays and weekends, for ARC and L-ARC with varying values of the localization parameter l on the Elec2 dataset.

🔼 This figure displays the results of applying ARC and L-ARC to a tumor segmentation task. The left panel shows the false negative rate (FNR) over time for both algorithms, demonstrating convergence to the target FNR. The center panel shows the average FNR across different datasets (Kvasir, CVC-ClinicDB, CVC-ColonDB, CVC-300, ETIS-LaribPolypDB), highlighting the improved fairness of L-ARC across data subpopulations. The right panel presents the average mask sizes, illustrating how L-ARC adjusts the size to manage FNR across subpopulations.
read the caption
Figure 4: Long-term FNR (left), average FNR across different data sources (center), and average mask size across different data sources (right) for ARC and L-ARC with varying values of the localization parameter l for the task of tumor segmentation [Fan et al., 2020].

🔼 This figure compares the performance of three different algorithms (ARC, Mondrian ARC, and L-ARC) for beam selection in a wireless network. The left-top panel shows the long-term risk achieved by each algorithm as a function of time. The left-bottom panel shows the average beam set size used by each algorithm as a function of the target risk. The right panel shows a heatmap of the signal-to-noise ratio (SNR) across the deployment area for each algorithm. The heatmaps show that L-ARC achieves a more uniform SNR level across the deployment area compared to the other two algorithms.
read the caption
Figure 5: Long-term risk (left-top), average beam set size (left-bottom), and SNR level across the deployment area (right) for ARC, Mondrian ARC, and L-ARC. The transmitter is denoted as a green circle and obstacles to propagation are shown as grey rectangles.
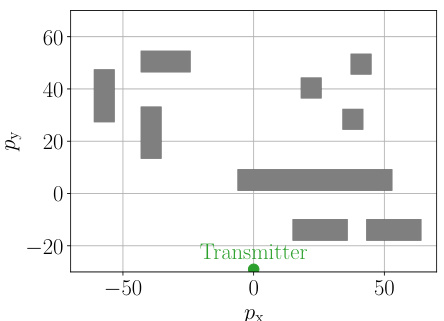
🔼 This figure illustrates the simulation setup used for the beam selection experiment in the paper. A single transmitter (shown as a green circle) is located in an urban environment with multiple buildings (grey rectangles). Receivers are uniformly distributed across the area. This setup simulates a real-world scenario where signal propagation is affected by obstacles, reflecting the complexity of beam selection in wireless networks.
read the caption
Figure 6: Network deployment assumed in the simulations. A single transmitter (green circle) communicates with receivers that are uniformly distributed in a scene containing multiple buildings (grey rectangles).

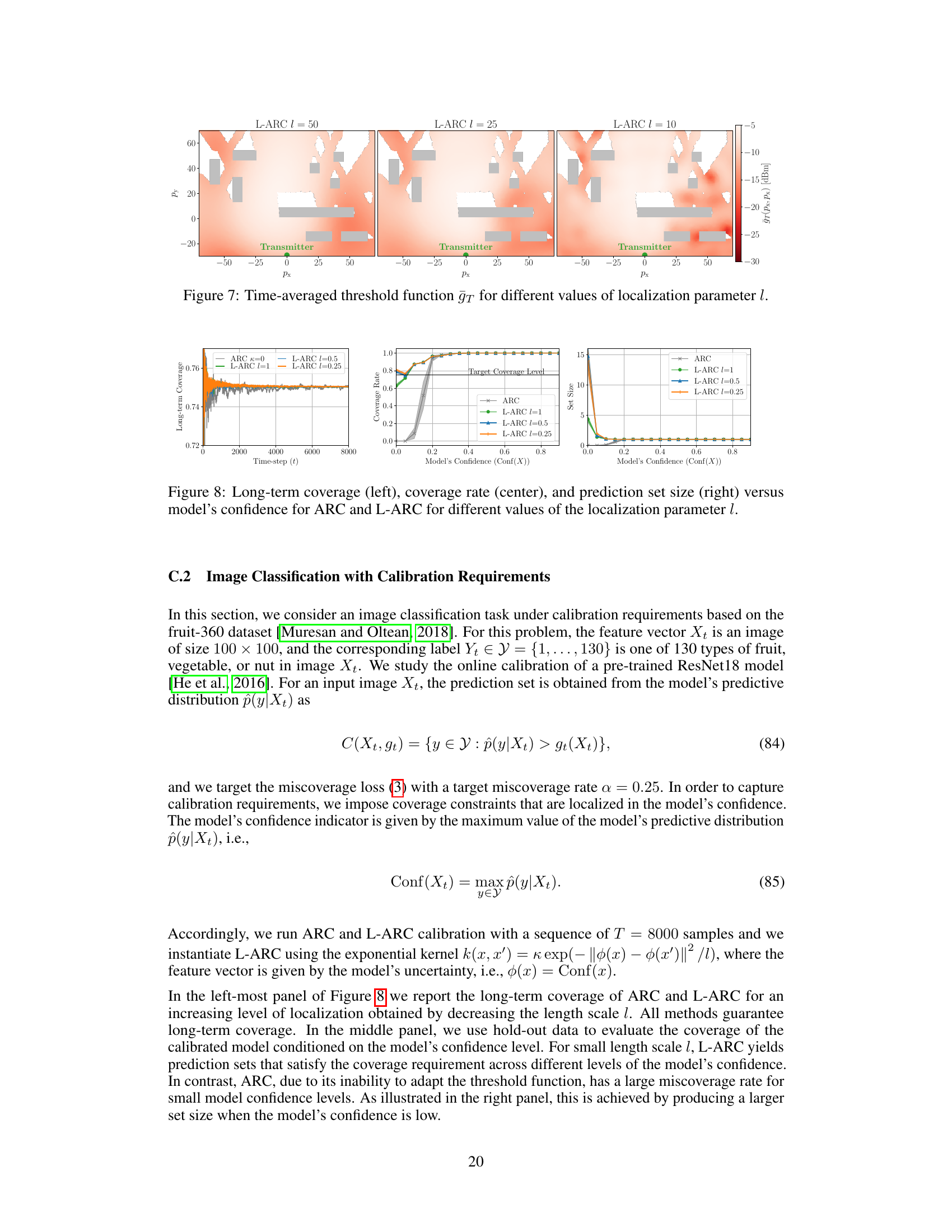
🔼 This figure visualizes the time-averaged threshold function (ḡT) produced by L-ARC for varying values of the localization parameter (l). Each subplot represents a different value of l, demonstrating how the threshold function changes as the degree of localization is altered. The color map indicates the threshold value, with warmer colors representing higher thresholds and cooler colors representing lower thresholds. The spatial distribution of the threshold reveals how L-ARC adapts the threshold based on the input features, aiming to provide localized risk control guarantees. The figure is relevant to showing how L-ARC tunes the decision-making threshold to account for variations in different subsets of the data or model uncertainties, with smaller values of l leading to more localization of risk control and greater adaptability to variations in specific areas. This relates directly to the core argument of the paper about localized risk control.
read the caption
Figure 7: Time-averaged threshold function ḡT for different values of localization parameter l.

🔼 This figure displays three plots showing the performance of ARC and L-ARC with varying localization parameters (l) for an image classification task. The left plot shows the long-term coverage over time steps. The center plot shows the coverage rate against the model’s confidence level. The right plot shows the set size as a function of model confidence. The plots show that L-ARC achieves better coverage control across different confidence levels compared to ARC, especially at lower confidence levels where set size increases to maintain coverage.
read the caption
Figure 8: Long-term coverage (left), coverage rate (center), and prediction set size (right) versus model's confidence for ARC and L-ARC for different values of the localization parameter l.
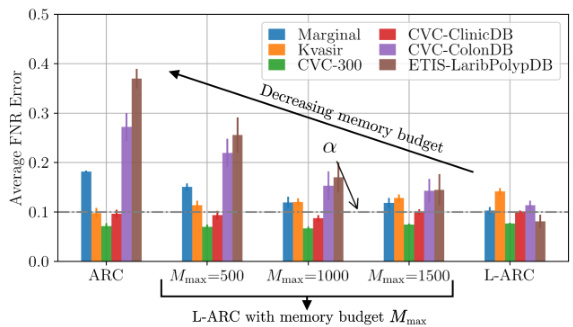
🔼 This figure shows the average false negative rate (FNR) achieved by ARC, L-ARC, and a memory-truncated version of L-ARC across different data subpopulations. The memory-truncated L-ARC uses a parameter, Mmax, to limit its memory usage, effectively performing a trade-off between the full L-ARC’s performance and computational efficiency. The results demonstrate that as Mmax increases (more memory is used), the performance of truncated L-ARC approaches that of the full L-ARC, while smaller Mmax values lead to performance closer to standard ARC. This illustrates the effect of memory constraints on the model’s localized risk control capabilities.
read the caption
Figure 9: FNR obtained by ARC, L-ARC, and L-ARC with limited memory budget Mmax ∈ {500, 1000, 1500}. As the memory budget increases, the localized risk control performance of L-ARC interpolates between ARC and L-ARC.
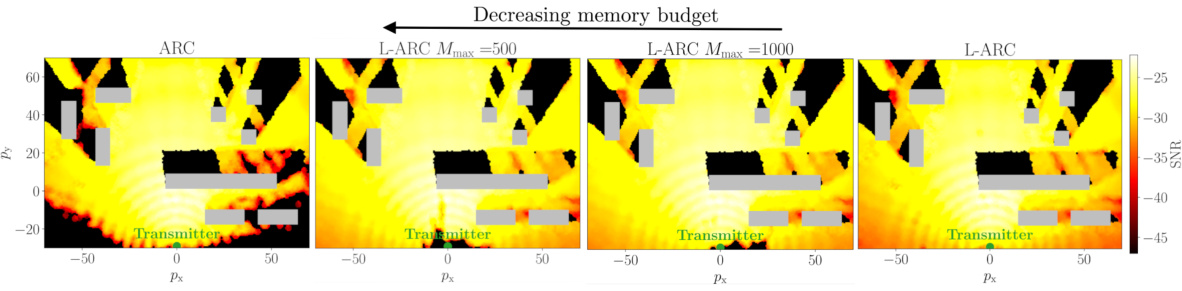
🔼 This figure compares the signal-to-noise ratio (SNR) performance across the deployment area for different memory budgets in the L-ARC algorithm. The green circle represents the transmitter location. Gray rectangles represent obstacles. The color intensity represents the SNR level; warmer colors indicate higher SNRs. The figure showcases how L-ARC’s ability to balance SNR across the deployment area changes with different memory constraints (Mmax). As Mmax decreases, the algorithm’s memory usage is reduced, which leads to a tradeoff in terms of SNR uniformity across the region. This demonstrates the effect of a memory constraint on L-ARC’s localized risk control, showing a balance between performance and memory efficiency.
read the caption
Figure 10: SNR across the deployment attained by L-ARC with limited memory budget Mmax.
Full paper#