Using Surrogates in Covariate-adjusted Response-adaptive Randomization Experiments with Delayed Outcomes

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with delayed outcomes, a common challenge in various fields. It offers a novel CARA design that significantly improves estimation efficiency by integrating surrogate information. This enhances the practicality and reliability of clinical trials and other experiments where immediate observation of primary outcomes is not feasible, opening new avenues for research.

Visual Insights

#

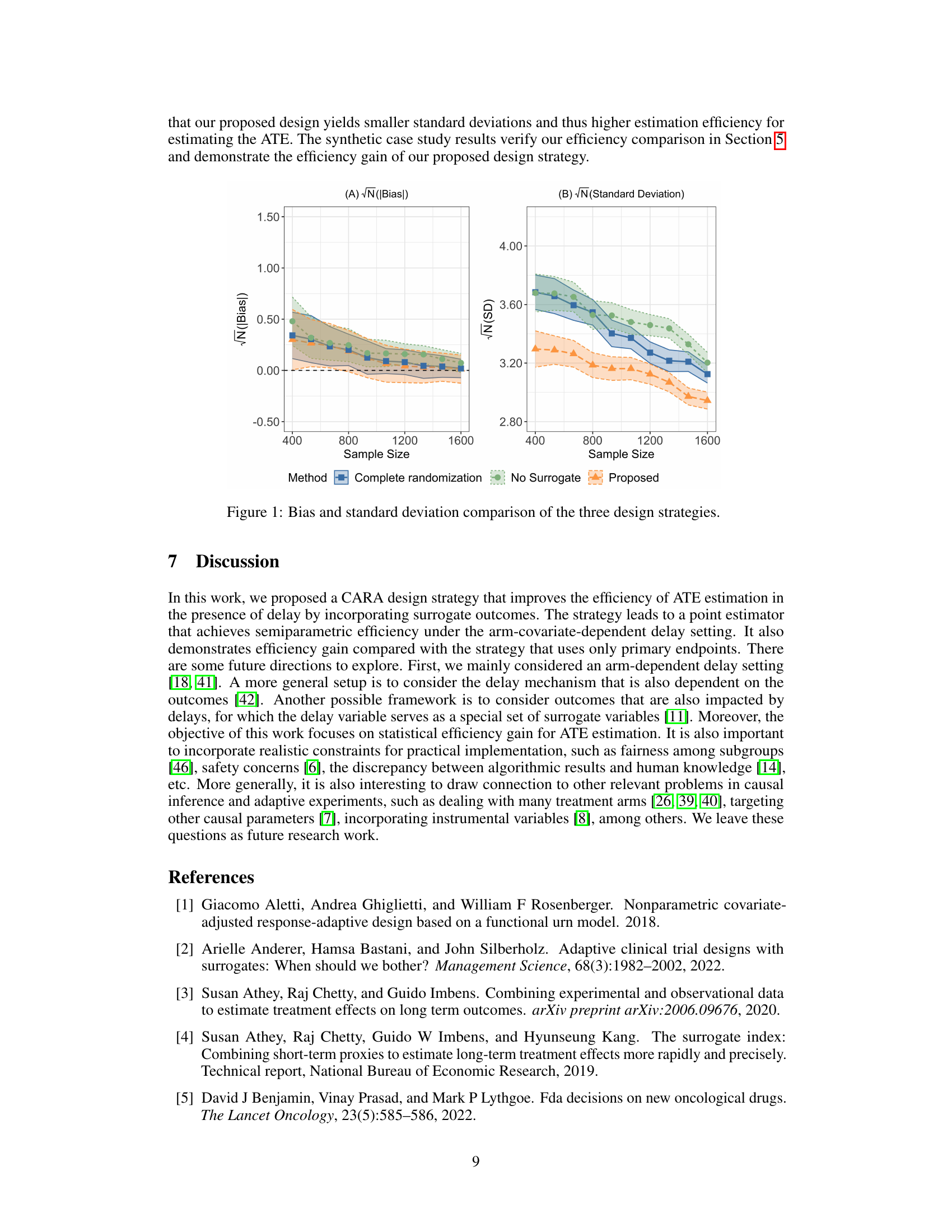
🔼 This figure compares the performance of three different design strategies in estimating the average treatment effect (ATE) based on bias and standard deviation. The three strategies are: (1) The proposed CARA design incorporating both primary and surrogate outcomes; (2) A complete randomization design using only delayed primary outcomes; (3) A CARA design using only primary outcomes. The x-axis represents the sample size, and the y-axis shows the bias (A) and standard deviation (B) of the ATE estimates. The results demonstrate that the proposed design has smaller bias and variance, indicating better estimation efficiency compared to the other two strategies.

read the caption

Figure 1: Bias and standard deviation comparison of the three design strategies.

🔼 This table presents the delay mechanism observed from real data in a synthetic case study based on an HIV trial. It shows the probability of observing the primary outcome (viral load) at different time points (T-t), stratified by treatment arm (X) and covariate (sex). The data demonstrates that the delay mechanism depends on both the treatment assignment and the covariate.

read the caption

Table 1: Delay mechanism from the real data

In-depth insights

#

CARA Design

#

Covariate-adjusted response-adaptive randomization (CARA) designs are a powerful class of experimental methods that combine the strengths of randomization and adaptive design. They enhance efficiency by strategically adjusting treatment allocations based on accumulating covariate and outcome data, making them particularly useful when dealing with heterogeneous treatment effects or limited sample sizes. The adaptive nature of CARA designs allows for more efficient use of resources and potentially greater precision in estimating treatment effects. However, successful implementation hinges on careful consideration of several factors, including the choice of an appropriate allocation rule, potential biases stemming from adaptive allocation, and the need for sufficient data at each stage to inform the allocation process. Furthermore, the assumptions underlying the statistical validity of CARA methods, particularly related to the nature and extent of missing data, require careful evaluation and appropriate handling in practical settings. Future research should focus on developing more robust and flexible CARA designs that can address these challenges in a wider array of applications.

Surrogate Use

#

The concept of ‘Surrogate Use’ in this context likely revolves around employing readily available surrogate markers to predict or estimate delayed primary outcomes. This strategy is particularly valuable in research settings where primary outcomes take a considerable time to materialize, such as long-term clinical trials investigating chronic diseases. Using surrogates offers several advantages: increased efficiency by expediting data collection and analysis, potentially reducing the overall duration and cost of the study, and mitigating the impact of missing data commonly associated with delayed outcomes. However, careful consideration of surrogate validity is critical. A poorly chosen surrogate can lead to biased or unreliable estimations of treatment effects. Therefore, a robust validation of the surrogate’s predictive power is crucial, ideally involving assessment of its correlation with the primary outcome under different treatment conditions. Careful consideration of potential biases and confounding factors is equally important when selecting and using surrogates to ensure the accuracy and reliability of the results.

Delayed Outcomes

#

The concept of ‘Delayed Outcomes’ in research is crucial, especially in longitudinal studies or clinical trials. Delays in observing outcomes introduce significant challenges, including missing data, inefficient estimation of treatment effects, and difficulty in making timely treatment decisions. The presence of a delay mechanism (the process governing the timing of outcomes) further complicates the analysis and requires careful consideration. For example, in clinical trials, delays might arise due to the time it takes for a treatment to show its effects or the time needed to measure specific outcomes. Strategies for handling delayed outcomes often involve imputation methods or survival analysis, but these approaches typically rely on assumptions that may not always be met. Incorporating surrogate outcomes (intermediate measures predictive of the primary outcome) can enhance the efficiency of estimation, particularly in response-adaptive randomized designs where treatment allocation is adjusted based on early data. However, the choice of a surrogate outcome is itself a critical step requiring validation, and careful consideration is required to minimize bias and improve the overall reliability of results. A critical evaluation of the delay mechanism is therefore essential, and consideration must be given to issues of causality and potential confounding factors influencing both outcome delays and the outcome itself.

Efficiency Gain

#

The concept of ‘Efficiency Gain’ in the context of a research paper likely refers to improvements achieved by a proposed method or design over existing approaches. This could manifest as a reduction in the number of participants needed to achieve a statistically significant result, faster convergence in iterative algorithms, or less computational cost for analysis. A thorough discussion would delve into the specifics of the gain, offering quantitative measures and comparing it to relevant baselines, such as traditional methods or prior state-of-the-art techniques. Statistical significance of the efficiency gains would also be paramount, ensuring the observed improvements are not merely due to random chance. The analysis should consider various scenarios and factors affecting efficiency, and the limitations of the gains should be clearly articulated to provide a balanced and comprehensive assessment of the contribution.

Future Work

#

The ‘Future Work’ section of a research paper on covariate-adjusted response-adaptive randomization (CARA) designs with delayed outcomes and surrogate endpoints would naturally explore several avenues. Extending the CARA design to handle more complex delay mechanisms is crucial, moving beyond arm-dependent delays to incorporate outcome-dependent delays, or even more intricate scenarios. Addressing multiple treatment arms would significantly increase the practical applicability of the design. Incorporating more sophisticated surrogate selection methods to improve the efficiency of using surrogate information is a key area of potential enhancement. Developing more robust statistical methods that are less sensitive to model misspecification or violations of assumptions is vital. Finally, conducting extensive simulations and real-world applications of the proposed methods are essential to rigorously evaluate its performance and practical implications in various clinical trial settings.

More visual insights

#

More on tables

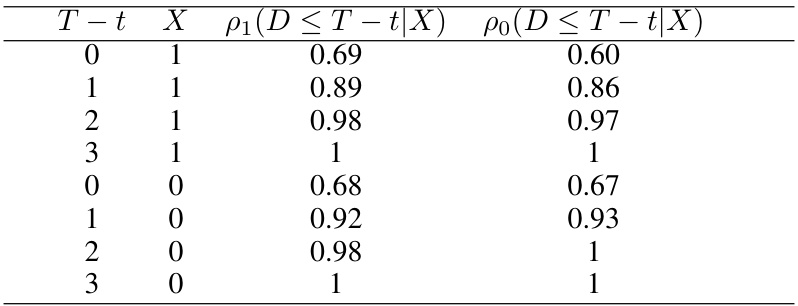
🔼 This table presents the probability of observing the primary outcome within a certain time frame (T-t), given the treatment arm (X=0 for control, X=1 for treatment). The data reflects the delay mechanism observed in a real-world HIV trial which inspired the study’s synthetic data generation.

read the caption

Table 1: Delay mechanism from the real data

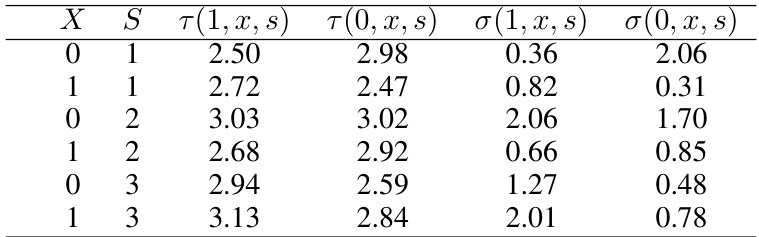
🔼 This table presents the parameters used in the synthetic data generation process for the continuous primary outcome variable (viral load). For each combination of covariate (sex: X=0 for female, X=1 for male) and surrogate outcome (WHO stage: S=1, 2, 3 representing asymptomatic, mild, and advanced symptoms, respectively), the table gives the mean of the potential outcomes under treatment (τ(1,x,s)) and control (τ(0,x,s)), as well as their standard deviations (σ(1,x,s) and σ(0,x,s)). These parameters are estimated from a real HIV trial and used to make the synthetic data realistic.

read the caption

Table 2: Parameters generated from real data (Continuous outcome)

Full paper

#