TL;DR#
Current music generation methods often lack physical realism. While differentiable digital signal processing (DDSP) offers improvements, it is limited in modeling complex physical phenomena like the vibration of strings. This necessitates highly accurate numerical methods like finite-difference time-domain (FDTD), but these are computationally expensive and lack the flexibility of neural networks.
This paper introduces Differentiable Modal Synthesis for Physical Modeling (DMSP) which leverages the efficiency of modal synthesis while incorporating the expressiveness of neural networks. DMSP achieves superior accuracy in simulating nonlinear string motion compared to existing methods and offers dynamic control over pitch and material properties, leading to more realistic sound synthesis. The availability of code and a demo further enhances the accessibility and impact of this research.
Key Takeaways#
Why does it matter?#
This paper is significant because it bridges the gap between machine learning and physics-based audio modeling, opening doors for more realistic and controllable music and sound synthesis. Its differentiable approach makes it easier to integrate physical models into neural networks, leading to more expressive and accurate audio generation. The model’s superior accuracy in string simulation also has implications for virtual reality, game development, and other areas where realistic physics simulation is critical.
Visual Insights#

🔼 This figure illustrates the overall architecture of the Differentiable Modal Synthesis for Physical Modeling (DMSP) system. It shows how the model takes physical properties (tension, stiffness, damping, initial conditions) and control parameters (pitch, time, pickup position) as inputs and produces both a visual representation of string motion (displacement over time and space) and the corresponding synthesized sound.
read the caption
Figure 1: System overview. The DMSP model encodes the physical properties of a string (e.g., tension, stiffness, damping, and initial conditions) to estimate the displacement of the string plucked at pitch at a given time ∈ [0,∞) and position ∈ Ω. By concatenating the DMSP outputs over the domain (x, t) ∈ Ω × [0, ∞), the simulated motion of the string can be visualized. Reading the outputs at a particular position x allows hearing the synthesized string sound, akin to listening with a stethoscope at the pickup position.

🔼 This table compares different methods for sound synthesis, including modal synthesis, finite-difference time-domain (FDTD), differentiable digital signal processing (DDSP), and the proposed differentiable modal synthesis for physical modeling (DMSP) and its hybrid version. It categorizes each method by whether it is a physical model, accounts for nonlinearities, is differentiable (allowing for gradient-based optimization), and its computational complexity in terms of pre-computation and synthesis.
read the caption
Table 1: Comparison between methods. Computational complexity refers to the inference scenario.
In-depth insights#
Diff Modal Synth#
Differentiable modal synthesis, a novel approach to sound generation, merges the precision of physical modeling with the flexibility of neural networks. By making the synthesis process differentiable, it allows for end-to-end training, optimizing the model parameters to match target sounds. This contrasts with traditional methods, often requiring separate optimization steps. The core idea involves representing sound using a sum of modes, each characterized by its frequency and amplitude. These modes are learned through a neural network, allowing for flexible control over timbre and dynamics, especially for complex instruments with nonlinear behavior, such as bowed strings or plucked instruments. The resulting model shows promise in generating realistic and expressive sounds, particularly as it allows for incorporating physical properties as inputs for finer control. However, further research is needed to explore the model’s limitations and potential for generating a wider range of sounds. Computational efficiency during inference is a key advantage but remains to be fully explored in various scenarios and for different instrument families.
Phys Model Sim#
A hypothetical research paper section titled ‘Phys Model Sim’ would likely delve into the physical modeling and simulation aspects of a system. This could involve creating mathematical representations of physical phenomena and then using computational methods to simulate the system’s behavior over time. The level of detail would depend on the complexity of the system being modeled. For instance, a simple model might use ordinary differential equations, while more complex systems could need partial differential equations or agent-based models. Validation would be crucial, comparing simulation results to experimental data or other established models. The section might also discuss the limitations of the model, highlighting any simplifying assumptions made and their impact on accuracy. A key focus would likely be on the trade-off between model complexity and computational cost, exploring different approaches to balance accuracy and efficiency. Finally, the practical applications of the simulation, such as design optimization or prediction, could be presented.
Neural Network#
A neural network is a computing system inspired by the biological neural networks that constitute animal brains. It is composed of interconnected nodes, or neurons, organized in layers (input, hidden, output). These networks are adept at learning complex patterns from data through a process called training. This involves adjusting the strength of connections (weights) between neurons to minimize the difference between predicted and actual outputs. Deep learning, a subfield of machine learning, utilizes deep neural networks with many layers, allowing for the extraction of increasingly abstract features from data. The architecture of the neural network, including the number of layers, neurons per layer, and connection types, is crucial for performance and depends heavily on the specific application. Various neural network architectures exist, each optimized for different tasks, such as image classification (Convolutional Neural Networks), sequential data processing (Recurrent Neural Networks), and natural language processing (Transformers). Training neural networks requires substantial computational resources and large datasets, highlighting the importance of efficient algorithms and hardware acceleration. The ability of neural networks to learn and generalize from data makes them powerful tools for diverse applications in various domains.
Nonlinear Strings#
The study of nonlinear string vibrations is crucial for realistic sound synthesis, as linear models fall short in capturing the complexities of real-world instruments. Nonlinearity introduces phenomena like pitch glide, inharmonicity, and phantom partials, significantly impacting timbre. The challenges in modeling nonlinear strings stem from the inherent complexity of the governing partial differential equations (PDEs). While linear models yield analytical solutions via modal decomposition, nonlinear PDEs often require numerical methods, such as finite-difference time-domain (FDTD) methods, for approximation. These methods can be computationally expensive, limiting real-time applications. Consequently, research focuses on efficient numerical techniques or approximations that capture the essence of nonlinear string behavior. The development of differentiable physical models, integrating neural networks with physical principles, offers a promising path to achieve both accuracy and efficiency in simulating nonlinear string vibrations for applications in music synthesis and beyond.
Future Research#
Future research directions stemming from this Differentiable Modal Synthesis (DMSP) for physical modeling of strings could explore several promising avenues. Extending DMSP to other instrument families, such as bowed strings, wind instruments, or percussion, would require adapting the underlying physics and incorporating appropriate features into the neural network architecture. Improving the model’s efficiency and scalability is crucial for real-time applications, potentially through architectural optimizations or leveraging more efficient neural network architectures. Investigating different loss functions and training strategies could enhance the model’s accuracy and generalization ability. For example, incorporating perceptual loss functions could lead to more musically pleasing results. Additionally, exploring the integration of DMSP with other neural audio synthesis techniques, such as those for reverberation or source separation, could enable more realistic and expressive sound generation. A thorough investigation of the model’s robustness to variations in input parameters and noise is warranted, especially considering real-world applications. Finally, exploring techniques for more effective parameter estimation, such as incorporating more sophisticated physical priors and physics-informed neural networks, holds significant potential for improving accuracy and efficiency.
More visual insights#
More on figures
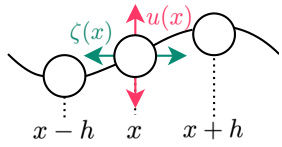
🔼 This figure shows a schematic representation of a planar string system. The string’s transverse displacement, u(x), and longitudinal displacement, ζ(x), are shown for a section of the string around point x. The string is shown as a series of interconnected mass points, indicating the discretization used in the numerical modeling of the string’s vibration. The arrows illustrate the directions of the transverse (u(x)) and longitudinal (ζ(x)) displacements.
read the caption
Figure 2: The planar string system.

🔼 This figure shows the architecture of the Differentiable Modal Synthesis for Physical Modeling (DMSP) model. The model takes physical properties of a string (initial condition, tension, stiffness, damping, and pitch) as input and uses a parameter encoder and a mode estimator to synthesize the sound. Amplitude and frequency modulation are applied to create an inharmonic pitch skeleton, making the sound more realistic. Both a hybrid model (using modal decomposition) and a fully neural network model are shown. The model produces an output waveform through a spectral modelling pipeline.
read the caption
Figure 3: Network architecture. DMSP synthesizes a pitch skeleton with an inharmonic structure, drawing upon overtones derived from the modes of the string. The modes can either be derived directly using the modal decomposition (DMSP-Hybrid, the hybrid of DMSP and Modal), or using the neural network trained to estimate the modes (DMSP, the fully-neural-network method). Yet, relying solely on modal frequencies and corresponding shape functions delineates a linear solution, which falls short of capturing the nuances of nonlinear string motion. To address this, DMSP introduces FM and AM blocks to modulate the modes of the linear solution. This modulation process enables DMSP to estimate the pitch skeleton of the nonlinear solution. Consequently, the output waveform is synthesized through the spectral modeling pipeline, incorporating both (in)harmonic components and the filtered noise.

🔼 This figure visualizes how the objective scores (SI-SDR, SDR, MSS, and Pitch) change with respect to variations in the physical parameters (x, κ, α, pa, and px). Each subplot represents a specific parameter, and the scores for both the Modal synthesis model and the DMSP model are shown as teal and pink dots, respectively. This allows for a direct comparison of model performance under differing physical conditions.
read the caption
Figure 5: Objective scores over the change of physical parameters.

🔼 This figure compares spectrograms generated by different models (Modal, DDSPish-XFM, DDSPish, DMSP, DMSP-Hybrid) against the ground truth (FDTD) for the test set. Each spectrogram visually represents the frequency content of the synthesized audio over time. The color intensity corresponds to the magnitude of the spectral components. The visual differences highlight how well each model captures the complex characteristics of a real string’s sound, including elements like pitch glide and phantom partials.
read the caption
Figure 6: Spectrogram of the synthesized samples on the test set.
🔼 This figure compares the spectrograms and displacement in space and time for different models, including the ground truth (FDTD). The spectrograms visualize the frequency content over time, while the displacement plots show the string’s movement in space and time. This provides a visual comparison of the models’ ability to capture both the sound and motion characteristics of a plucked string.
read the caption
Figure 7: Spectrograms and state samples of the synthesized samples on the test set. For the spectrograms shown in the first column, the intensity of the frequency (vertical axis) component for time (horizontal axis) is expressed as brightness, and for the states shown in the second column, the displacement (vertical axis) for space (horizontal axis).
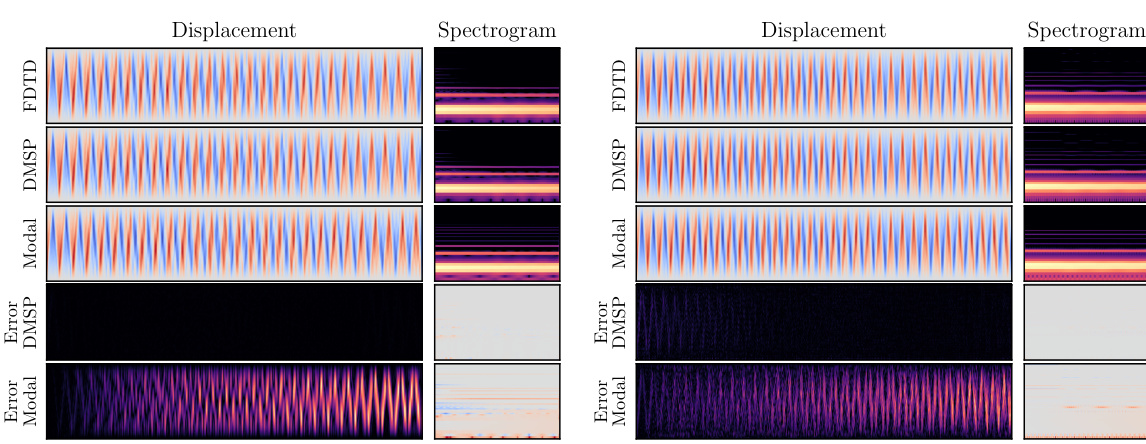
🔼 This figure visualizes the simulated string displacement over time and space for different methods (FDTD, DMSP, Modal). The top rows show the displacement and spectrogram for each method. The bottom rows show the error between each method and the FDTD ground truth. The visualizations allow for a qualitative comparison of the accuracy of the different methods in simulating both the motion and sound of the string.
read the caption
Figure 8: Simulated string state visualization.
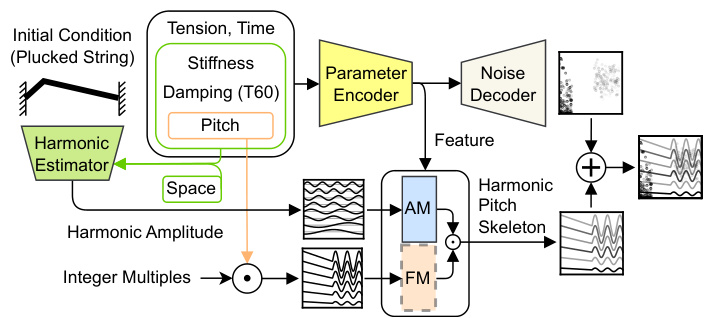
🔼 This figure shows the architecture of the Differentiable Modal Synthesis for Physical Modeling (DMSP) model. The model takes physical properties of a string (initial conditions, tension, stiffness, damping, and pitch) as input. It uses a mode estimator to determine the modes of vibration of the string, which are then modulated by amplitude and frequency modulation (AM/FM) blocks to account for non-linear behavior. The output is a synthesized waveform that includes harmonic and inharmonic components and noise.
read the caption
Figure 3: Network architecture. DMSP synthesizes a pitch skeleton with an inharmonic structure, drawing upon overtones derived from the modes of the string. The modes can either be derived directly using the modal decomposition (DMSP-Hybrid, the hybrid of DMSP and Modal), or using the neural network trained to estimate the modes (DMSP, the fully-neural-network method). Yet, relying solely on modal frequencies and corresponding shape functions delineates a linear solution, which falls short of capturing the nuances of nonlinear string motion. To address this, DMSP introduces FM and AM blocks to modulate the modes of the linear solution. This modulation process enables DMSP to estimate the pitch skeleton of the nonlinear solution. Consequently, the output waveform is synthesized through the spectral modeling pipeline, incorporating both (in)harmonic components and the filtered noise.
More on tables
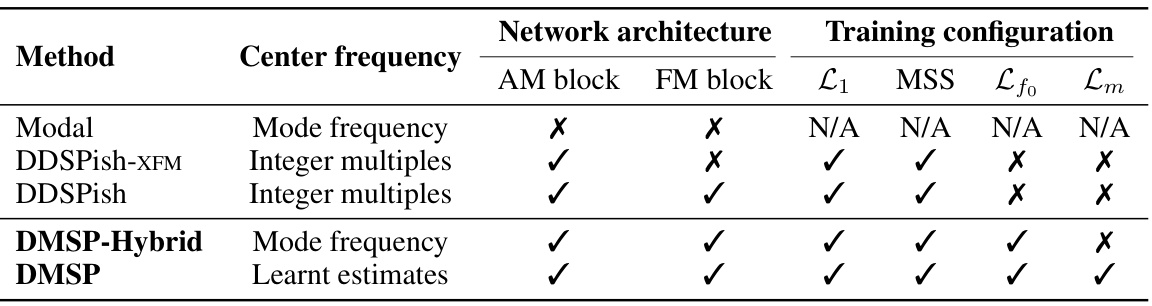
🔼 This table compares different models used in the paper for sound synthesis, highlighting their key differences in terms of center frequency determination (mode frequency vs. integer multiples), network architecture components (AM and FM blocks), and training configurations (loss functions used). It provides a structured overview of how each model approaches the task, facilitating a direct comparison of their characteristics.
read the caption
Table 2: Comparison between the baselines and the proposed models.
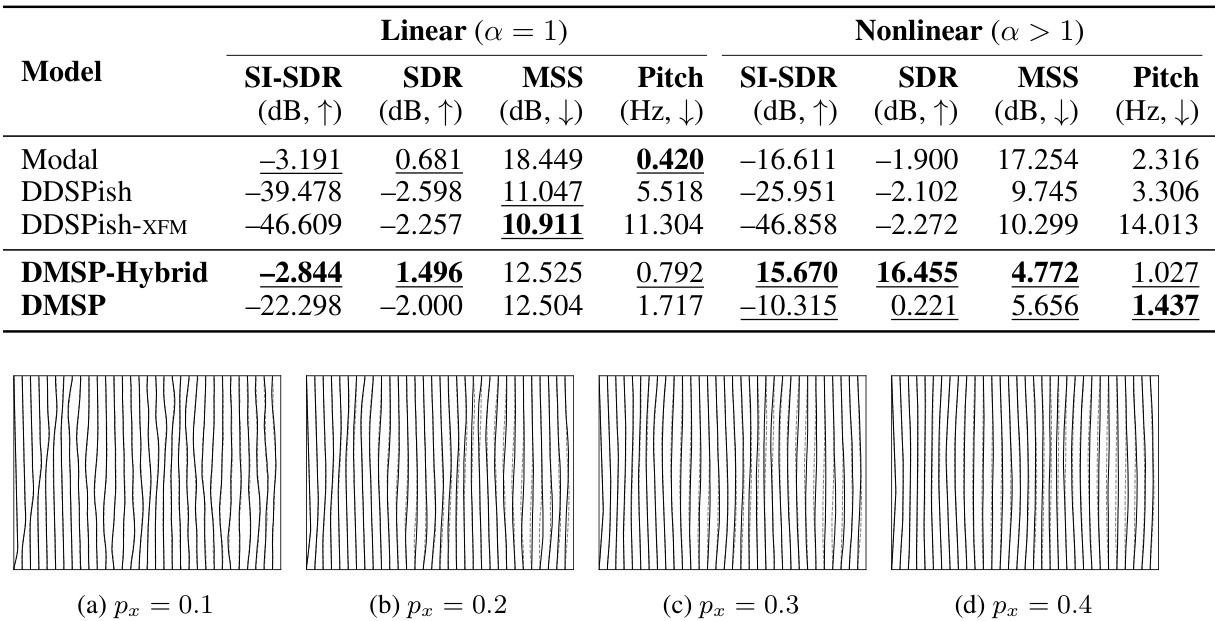
🔼 This table presents a comparison of the synthesis results for four different models (Modal, DDSPish, DDSPish-XFM, DMSP-Hybrid, and DMSP) across two categories of strings: linear (a = 1) and nonlinear (a > 1). For each model and string type, the table shows the SI-SDR (scale-invariant signal-to-distortion ratio), SDR (signal-to-distortion ratio), MSS (multi-scale spectral distance), and Pitch (pitch difference in Hz). Higher SI-SDR and SDR values indicate better sound quality, while a lower MSS value indicates better spectral similarity to the ground truth. Lower Pitch values represent better pitch accuracy. The results highlight the superior performance of DMSP and DMSP-Hybrid, particularly in the nonlinear string case, in terms of both sound and pitch accuracy.
read the caption
Table 3: Synthesis Results
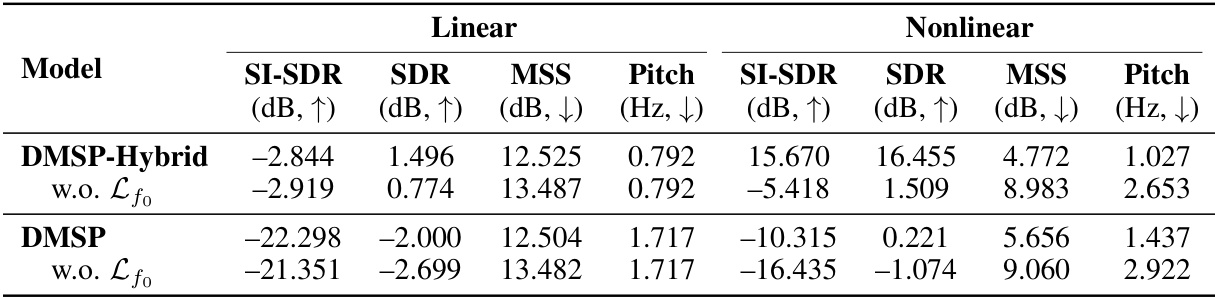
🔼 This table presents the ablation study results, comparing the performance of DMSP-Hybrid and DMSP models with and without the pitch loss (Lfo). The results are shown in terms of SI-SDR (scale-invariant signal-to-distortion ratio), SDR (signal-to-distortion ratio), MSS (multi-scale spectral) loss, and pitch difference (in Hz) for both linear and nonlinear string scenarios. This table helps to demonstrate the impact of the pitch loss function on the overall performance of the models.
read the caption
Table 4: Ablation Study

🔼 This table shows the minimum and maximum values used for sampling each of the PDE parameters during the data generation phase for training and testing the models. The parameters represent physical properties of the string, such as tension, stiffness, and damping, as well as the initial plucking conditions. The ranges are designed to encompass a variety of string behaviors, from linear to highly nonlinear.
read the caption
Table 5: PDE parameter sampling range
Full paper#