TL;DR#
Generative diffusion models excel at generating realistic data, but integrating constraints remains a challenge. Existing methods either condition models, which doesn’t guarantee constraint satisfaction, or apply post-processing corrections, potentially degrading output quality. These limitations hinder diffusion model applications in domains requiring strict adherence to specifications.
This paper introduces Projected Diffusion Models (PDM), addressing these limitations. PDM incorporates constraints directly into the core sampling process via iterative projection steps. This ensures generated data rigorously adheres to the constraints while maintaining the model’s original objective of capturing the true data distribution. The effectiveness of PDM is validated on various applications with diverse constraints, showcasing improved constraint satisfaction and superior output quality compared to existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with generative models and constraint satisfaction. It offers a novel approach to integrate constraints directly into the generative process, overcoming limitations of existing methods. This opens new avenues for research in various fields requiring adherence to strict specifications, such as engineering design, robotics, and material science.
Visual Insights#

🔼 This figure compares the performance of Projected Diffusion Models (PDM) and conditional models in a physics-informed motion experiment. The y-axis represents the constraint violation, while the x-axis represents the time step during the sampling process. The blue line shows the constraint violation for PDM, demonstrating that it converges to a feasible solution (constraint violation of 0) as the sampling progresses. In contrast, the red line represents the constraint violation for the conditional model, which remains high, indicating a failure to satisfy the constraints. This illustrates PDM’s ability to handle constraints effectively by iteratively projecting the sampling process onto the constraint set.
read the caption
Figure 1: Sampling steps failing to converge to feasible solutions in conditional models (red) while minimizing the constraint divergence to 0 under PDM (blue).

🔼 This table compares the performance of the proposed Projected Diffusion Model (PDM) against the state-of-the-art PhysDiff model on the HumanML3D dataset for 3D human motion generation. It shows that PDM achieves zero penetration and floatation violations, unlike PhysDiff, which shows some errors. The FID (Fréchet Inception Distance) scores are also included as a measure of image quality.
read the caption
Table 1: PDM performance compared to (best) PhysDiff results on HumanML3D.
In-depth insights#
Constrained Diffusion#
Constrained diffusion models address a critical limitation of traditional diffusion models: the inability to guarantee adherence to predefined constraints during data generation. Standard diffusion models excel at generating realistic data but often struggle when the output needs to meet specific criteria, such as physical laws or design specifications. Constrained diffusion methods aim to overcome this by explicitly incorporating constraints into the sampling process. This often involves reformulating the sampling as a constrained optimization problem, ensuring that the generated data remains within the specified bounds. Different approaches exist, including iterative projection methods which repeatedly project the generated sample onto the constraint set, ensuring compliance at each step, and methods that directly incorporate constraints into the score function or the diffusion process itself. The choice of approach depends on the nature and complexity of the constraints, as well as the computational resources available. The key benefit of constrained diffusion is the ability to generate high-fidelity data that simultaneously satisfies the user-specified criteria, opening new possibilities for applications in diverse fields, particularly those with stringent requirements for data validity and reliability.
PDM Framework#
The Projected Diffusion Model (PDM) framework presents a novel approach to integrating constraints into the generative process of diffusion models. Instead of relying on post-processing or conditioning techniques, PDM reframes the sampling process as a constrained optimization problem. This allows for direct incorporation of constraints, ensuring adherence without compromising the fidelity of generated data. The core innovation lies in the iterative projection of the diffusion sampling steps onto constraint sets. This iterative refinement guarantees feasibility while aligning the generated samples with the original data distribution. Theoretical justifications provided in the paper support PDM’s ability to maintain data fidelity while adhering to constraints, offering a significant advantage over prior methods. The effectiveness of the PDM framework is demonstrated through various experiments across diverse domains, highlighting its versatility and robustness in handling both convex and non-convex constraints.
Iterative Projection#
The concept of “Iterative Projection” in the context of constrained generative models, particularly diffusion models, is a powerful technique for ensuring that generated samples adhere to specified constraints. The core idea involves iteratively refining generated samples by projecting them onto the feasible region defined by the constraints. This iterative process, unlike single-step projections, gradually steers the data distribution toward satisfying the constraints while minimizing deviations from the original generative model’s objective. The iterative nature is crucial because it allows for the handling of complex, potentially non-convex constraints, where a single projection might not be sufficient to guarantee feasibility. Each projection step acts as a correction, pulling the sample closer to the constraint set without significantly disrupting the underlying generative process. The effectiveness of this method relies on the choice of projection operator, which should ideally find the closest feasible point to the current sample to minimize distortion. The iterative nature also allows for incorporating error correction and noise management strategies. This process ensures not just constraint satisfaction but also attempts to optimize the original objective of the generative model, leading to higher-quality samples that closely resemble the true data distribution and meet the required criteria.
Theoretical Support#
The theoretical support section of a research paper on Projected Diffusion Models (PDMs) would ideally provide a rigorous mathematical framework justifying the model’s ability to satisfy constraints while preserving data fidelity. Key aspects to cover would include formal proofs for the convergence of the iterative projection steps to a feasible solution, demonstrating that the PDM sampling process adheres to imposed constraints without significantly deviating from the original data distribution. Furthermore, a theoretical analysis demonstrating the relationship between the PDM objective function and the original generative model’s objective function is crucial. This analysis would ideally prove that optimizing the PDM objective maintains alignment with the original goal of accurate data generation. A discussion on the types of constraints (convex vs. non-convex) that the theoretical framework supports is essential, along with an analysis of the computational complexity of the proposed projection methods. The theoretical analysis should also address the impact of noise in the diffusion process on constraint satisfaction and provide bounds on constraint violation. Finally, the theoretical support section should establish the conditions under which the proposed algorithm converges, ideally with quantifiable convergence rates. A strong theoretical foundation enhances the credibility and impact of the research by providing a solid mathematical underpinning for the empirical results.
Future of PDM#
The future of Projected Diffusion Models (PDMs) is bright, given their ability to elegantly integrate constraints into the generative process. Further research should focus on scaling PDMs to handle significantly larger datasets and more complex, high-dimensional constraint spaces. This includes investigating more efficient projection methods and exploring alternative optimization strategies to reduce computational cost. Another key area is expanding the types of constraints that PDMs can effectively manage. This could involve developing novel techniques to handle non-convex, non-differentiable, and implicitly defined constraints, such as those arising in many real-world applications. Improving theoretical understanding of PDM’s convergence properties and error bounds is also crucial. This will enable more robust and predictable generation of high-quality, constraint-satisfying data. Finally, exploring the applications of PDMs across a broader range of scientific and engineering domains will undoubtedly unearth new and innovative uses. Areas of particular interest include materials science, drug discovery, and robotics, where precise control over generative processes is paramount.
More visual insights#
More on figures
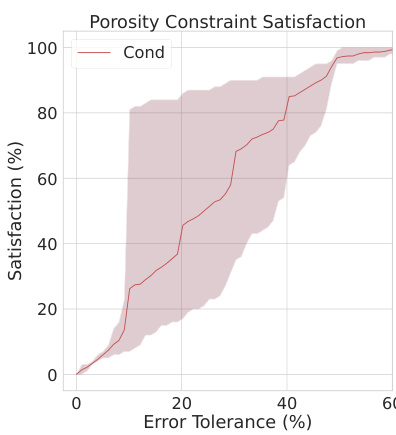
🔼 This figure shows the frequency of constraint satisfaction achieved by a conditional diffusion model for varying error tolerances in a porosity constraint satisfaction experiment. The y-axis represents the percentage of runs that satisfy the constraint within a given error tolerance (x-axis). It illustrates that even a state-of-the-art conditional model struggles to reliably satisfy the constraint, highlighting the challenges in ensuring adherence to strict specifications using conventional methods.
read the caption
Figure 2: Conditional diffusion model (Cond): Frequency of porosity constraint satisfaction (y-axis) within an error tolerance (x-axis) over 100 runs.

🔼 This figure visualizes the results of generating microstructures with varying porosity constraints. It compares the generated microstructures from four different methods: Ground truth (real microstructures), PDM (Projected Diffusion Models), Cond (Conditional Diffusion Models), Post+ (Conditional Diffusion Models with post-processing), and Cond+ (Conditional Diffusion Models with post-processing and projection). Each row shows the generated microstructures for a different porosity level (10%, 30%, and 50%). The FID scores (Fréchet Inception Distance), a measure of image quality and similarity to the real data, are provided for each method. The figure demonstrates PDM’s ability to generate high-fidelity microstructures while adhering to the specified porosity constraints, compared to other methods that struggle with accuracy or image quality.
read the caption
Figure 3: Porosity constrained microstructure visualization at varying of the imposed porosity constraint amounts (P) and FID scores.

🔼 This figure compares the results of PDM and a conditional model for 3D human motion generation. The left side shows a sequence of frames generated using the PDM approach, which achieves a Fréchet Inception Distance (FID) score of 0.71. The right side displays frames from a conditional model, resulting in an FID score of 0.63. The lower FID score for PDM indicates better adherence to the true data distribution. Importantly, the PDM-generated motion adheres strictly to physical constraints (e.g., the figure’s feet remain on the ground).
read the caption
Figure 4: PDM (left, FID: 0.71) and conditional (Cond) (right, FID: 0.63) generation.

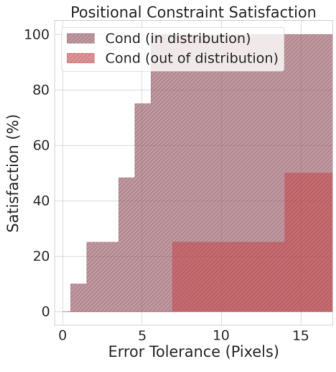
🔼 This figure shows two examples of constrained trajectories generated by the Projected Diffusion Model (PDM) in a path planning scenario. The left panel shows a trajectory on one type of topography (Tp1), and the right panel shows a trajectory on a different topography (Tp2). Both topographies feature a number of obstacles (grey and red circles and squares) that the planned trajectory must avoid. The planned trajectory is shown as a purple line connecting a series of points generated by PDM. The starting point of each trajectory is shown as a small green circle, and the ending point is shown as a small purple circle.
read the caption
Figure 5: Constrained trajectories synthetized by PDM on two topographies (Tp1, left and Tp2, right).
🔼 This figure illustrates the effectiveness of Projected Diffusion Models (PDM) compared to conditional models in converging to feasible solutions during sampling. The red line shows a conditional model’s constraint violations during sampling steps; it fails to converge to feasible solutions. The blue line represents PDM; it successfully steers the sampling process towards feasible solutions, minimizing constraint violations over time.
read the caption
Figure 1: Sampling steps failing to converge to feasible solutions in conditional models (red) while minimizing the constraint divergence to 0 under PDM (blue).
🔼 This figure shows the performance of a conditional diffusion model (Cond) in satisfying porosity constraints in a material science experiment. The y-axis represents the percentage of times the model generated samples that met the porosity constraints, while the x-axis represents the allowed error tolerance in percentage. The graph demonstrates that even the state-of-the-art conditional model struggles to consistently satisfy the constraints. This highlights the challenge of controlling generative models to meet precise specifications.
read the caption
Figure 2: Conditional diffusion model (Cond): Frequency of porosity constraint satisfaction (y-axis) within an error tolerance (x-axis) over 100 runs.

🔼 This figure compares the results of different generative models in creating microstructures with varying porosity levels. The ‘Ground’ column shows real microstructures with different porosities (P%). The ‘PDM’ column shows the results obtained using the proposed Projected Diffusion Model. The other columns display the results from conditional diffusion models (‘Cond’), conditional models with post-processing (‘Cond+’), and models using only post-processing (‘Post+’). The FID scores (Fréchet Inception Distance) are provided below the images, indicating the image quality. The figure illustrates that PDM excels at generating realistic microstructures that meet the specified porosity constraints, while maintaining high image quality.
read the caption
Figure 3: Porosity constrained microstructure visualization at varying of the imposed porosity constraint amounts (P) and FID scores.

🔼 This figure shows the results of the physics-informed motion experiment, comparing the ground truth images with the outputs generated by PDM, a post-processing projection method (Post+), a conditional model with post-processing projection (Cond+), and a conditional model (Cond). The experiment is performed under both in-distribution (Earth) and out-of-distribution (Moon) constraint conditions. Each row represents a time step, showing the object’s position across different methods. The results show that PDM successfully satisfies the constraints in both scenarios, while other methods show various degrees of violation.
read the caption
Figure 7: Sequential stages of the physics-informed models for in-distribution (Earth) and out-of-distribution (Moon) constraint imposition.

🔼 This figure illustrates the difference in constraint satisfaction between a conditional model and PDM. The red line shows the constraint violation of a conditional model across sampling steps, where the model fails to generate outputs satisfying the specified constraints. In contrast, the blue line shows the constraint violation under PDM, demonstrating how the iterative projection process effectively steers the generated data distribution toward the feasible region. This result is discussed to highlight the advantage of PDM’s constraint satisfaction compared to the traditional conditioning approach in diffusion models.
read the caption
Figure 1: Sampling steps failing to converge to feasible solutions in conditional models (red) while minimizing the constraint divergence to 0 under PDM (blue).

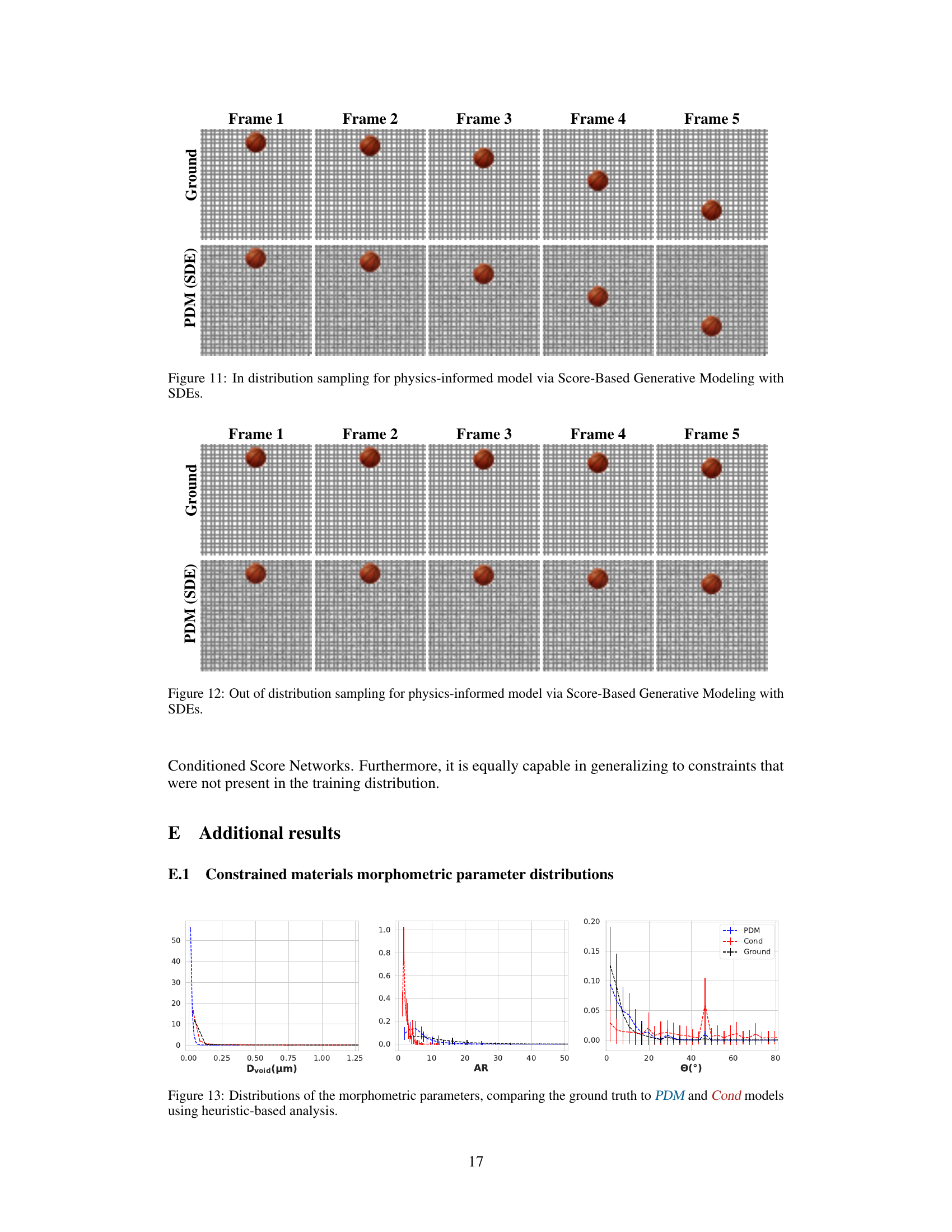
🔼 This figure visualizes the results of the physics-informed motion experiment, specifically focusing on in-distribution sampling. It presents a comparison between the ground truth (top row) and samples generated by the Projected Diffusion Model (PDM) using Stochastic Differential Equations (SDEs) (bottom row). Each row displays a sequence of five frames, showing the simulated motion of an object over time. The goal is to assess how accurately the PDM’s generation matches the ground truth, particularly given physical constraints (like gravity). The close similarity between the top and bottom rows suggests that PDM successfully generates realistic motion adhering to the specified physical laws.
read the caption
Figure 11: In distribution sampling for physics-informed model via Score-Based Generative Modeling with SDEs.
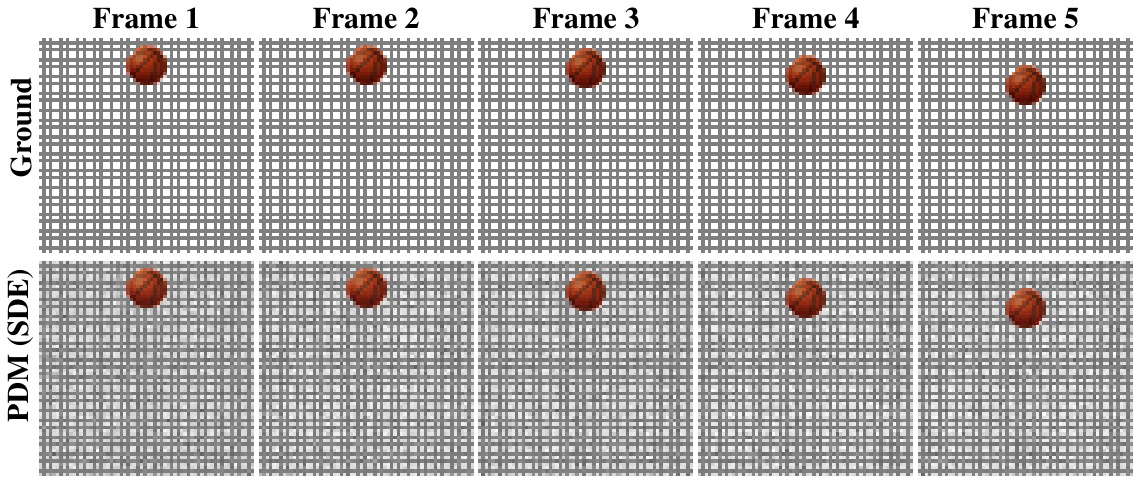
🔼 This figure shows the results of in-distribution sampling for a physics-informed model using Score-Based Generative Modeling with Stochastic Differential Equations (SDEs). It visually compares five frames of ground truth data (top row) with five corresponding frames generated by the PDM (bottom row). Both the ground truth and the PDM-generated frames depict a ball falling under the influence of gravity on a grid background. The comparison highlights the model’s ability to accurately generate physically realistic motion in a controlled setting.
read the caption
Figure 11: In distribution sampling for physics-informed model via Score-Based Generative Modeling with SDES.

🔼 The figure shows the convergence of the sampling process to feasible solutions for Projected Diffusion Models (PDM) compared to conditional models. The x-axis represents the time step during the sampling process, and the y-axis represents the constraint violation. The blue line shows the constraint violation for PDM, and the red line shows the constraint violation for conditional models. The figure shows that PDM converges to a feasible solution much faster than conditional models and that the constraint violation for PDM is much lower than that for conditional models. This demonstrates that PDM is more effective at satisfying constraints than conditional models.
read the caption
Figure 1: Sampling steps failing to converge to feasible solutions in conditional models (red) while minimizing the constraint divergence to 0 under PDM (blue).

🔼 This figure compares the performance of Projected Diffusion Models (PDM) and Conditional Models in terms of their ability to converge to feasible solutions. The x-axis represents the time step in the sampling process, and the y-axis represents the constraint violation. The blue line shows the constraint violation for PDM, which steadily decreases to zero. The red line shows the constraint violation for Conditional Models, which fails to converge to a feasible solution. This demonstrates that PDM is more effective than Conditional Models at satisfying constraints.
read the caption
Figure 1: Sampling steps failing to converge to feasible solutions in conditional models (red) while minimizing the constraint divergence to 0 under PDM (blue).

🔼 This figure shows the results of iterative projections using a model trained with a variational lower bound objective. The top row shows the results for the physics-informed motion experiment, and the bottom row shows the results for the material generation experiment. The figure demonstrates that the iterative projection method is able to generate high-quality samples that satisfy the constraints, even when the training data does not.
read the caption
Figure 15: Iterative projections using model trained with variational lower bound objective.
More on tables
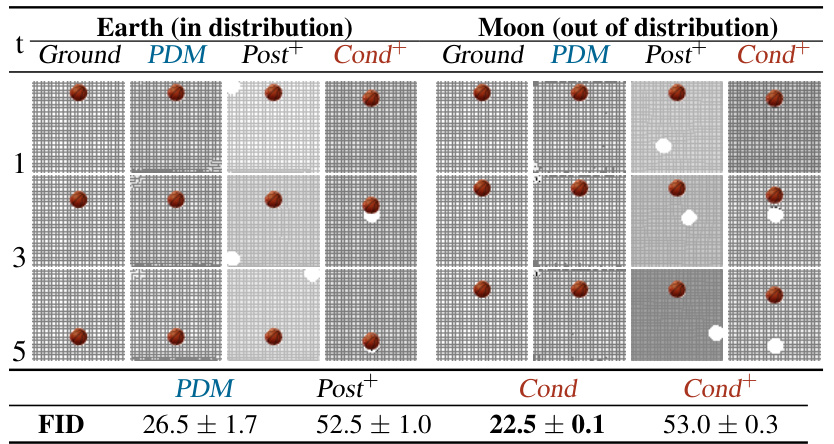
🔼 This table visually presents the generated samples from four different methods (Ground truth, PDM, Post+, and Cond+) for both in-distribution (Earth) and out-of-distribution (Moon) scenarios. It showcases the ability of PDM to accurately generate samples that adhere to the physical constraints, even when the constraints are out of the training data distribution. The other methods struggle with accurate constraint satisfaction. FID scores are included to show how constraint satisfaction impacts image quality. The images represent sequential stages (t=1,3,5) of an object falling under the influence of gravity.
read the caption
Table 7: Sequential stages of the physics-informed models for in-distribution (Earth) and out-of-distribution (Moon) constraint imposition.
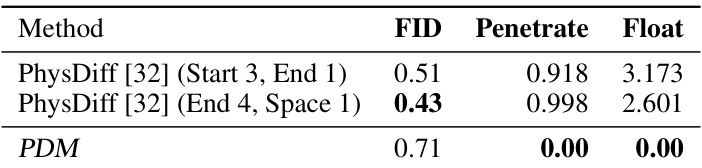
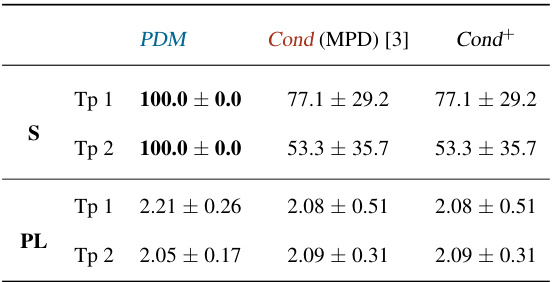
🔼 This table compares the performance of the proposed Projected Diffusion Model (PDM) against the state-of-the-art method PhysDiff on the HumanML3D dataset. The comparison is based on three metrics: FID (Fréchet Inception Distance), which measures the quality of generated samples; Penetrate, representing the average distance the generated figure penetrates the ground; and Float, showing the average distance the figure floats above the ground. Lower values are better for Penetrate and Float, indicating fewer physical violations. The results demonstrate that PDM achieves superior results, showing no physical constraint violations while maintaining a competitive FID score.
read the caption
Table 1: PDM performance compared to (best) PhysDiff results on HumanML3D.

🔼 This table presents the average time it takes to generate a single sample using different methods across four distinct experimental settings. The settings include: Constrained Materials, 3D Human Motion, Constrained Trajectories, and Physics-informed Motion. For each setting, the table shows the time taken by four approaches: PDM, Post+, Cond, and Cond+. The PDM approach is the proposed method; Post+ applies a projection step after the generation process; Cond employs a conditional diffusion model; and Cond+ adds post-processing projection to a conditional diffusion model. Times are in seconds. The asterisk indicates that the computation for these particular methods were done using CPU instead of the GPU, leading to considerably longer processing time.
read the caption
Table 2: Average sampling run-time in seconds.
Full paper#