↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph representation learning is crucial for analyzing complex systems represented as graphs. However, existing methods like graph autoencoders (GAEs) often suffer from the over-smoothing problem, where repeated information propagation leads to indistinguishable node representations. This hinders their effectiveness in various downstream tasks, such as node and graph classification. Additionally, many GAEs focus mainly on node-level information and lack robust universal representation for multiple tasks.
To address these issues, the paper introduces HC-GAE, a hierarchical cluster-based graph autoencoder. HC-GAE tackles over-smoothing by employing hard node assignment to decompose the graph into isolated subgraphs. This prevents information from over-propagating during encoding. In addition, it utilizes soft node assignment during decoding to reconstruct the graph structure and extract both node-level and graph-level representations. The experimental results demonstrate that HC-GAE outperforms existing methods on real-world datasets for node and graph classification tasks, showcasing its effectiveness in handling over-smoothing and generating robust representations for multiple downstream tasks.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles the over-smoothing problem in graph autoencoders, a significant challenge in graph representation learning. By introducing a hierarchical cluster-based approach, it offers improved performance for both node and graph classification tasks, opening new avenues for research in self-supervised graph representation learning and various downstream applications. The proposed method’s robustness to graph perturbations and its ability to generate effective representations for multiple tasks are also valuable contributions to the field.
Visual Insights#
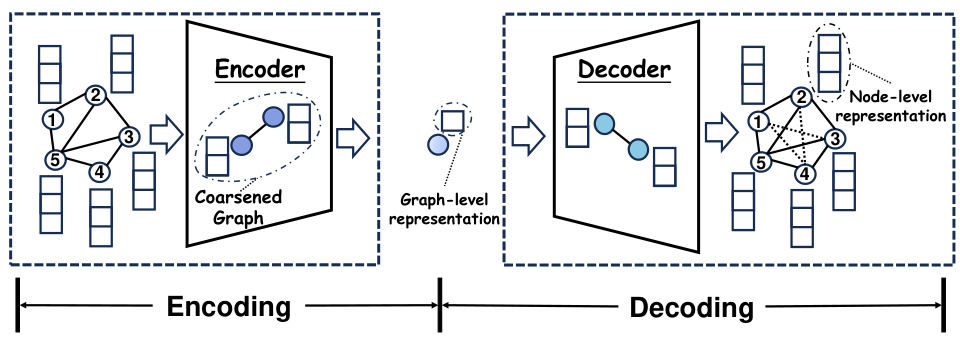
This figure illustrates the overall architecture of the Hierarchical Cluster-based Graph Auto-Encoder (HC-GAE) model. The HC-GAE model consists of two main stages: encoding and decoding. During the encoding stage, an input graph is compressed by the encoder into a coarsened graph which represents the graph-level representation of the input. This coarsened graph is then processed by the decoder to reconstruct the original input graph, thus producing a node-level representation. The encoding stage involves a series of compressing operations performed layer-wise, and the decoding stage involves an expansion procedure. The model is designed to learn effective structural characteristics for graph data analysis, using both graph-level and node-level representations.

This table presents the characteristics of five datasets used for node classification in the paper. For each dataset, it lists the number of nodes, edges, features per node, and the number of classes.
In-depth insights#
HC-GAE: A Deep Dive#
HC-GAE: A Deep Dive would explore the hierarchical cluster-based graph autoencoder’s architecture and functionality. It would delve into the hard node assignment during encoding, showing how it decomposes the graph into subgraphs, enabling efficient feature extraction. The soft node assignment in the decoder would be examined, revealing its role in reconstructing the original graph structure. The analysis would highlight the bidirectional hierarchical feature extraction enabled by this unique design. A key aspect would be analyzing how HC-GAE mitigates over-smoothing, a common problem in graph neural networks, by limiting information propagation within separated subgraphs. The effectiveness of the proposed loss function, integrating both local and global graph information, would also be examined to improve the overall performance. Finally, the ‘Deep Dive’ would cover the experimental results, demonstrating the model’s effectiveness on various real-world datasets for node and graph classification tasks, and how it compares to existing state-of-the-art models.
Hierarchical Clustering#
Hierarchical clustering, in the context of graph representation learning, offers a powerful technique for managing complexity and extracting hierarchical features. By recursively partitioning the graph into smaller, more manageable subgraphs, it enables the model to learn both local and global structural information. The choice of linkage criteria (e.g., single, complete, average) significantly influences the resulting clusters, impacting downstream task performance. This hierarchical decomposition also addresses the over-smoothing problem often encountered in graph neural networks, as information flow is contained within subgraphs. However, the computational cost of hierarchical clustering can be substantial, especially for large graphs. Balancing the granularity of the hierarchy is crucial; too coarse a partition may lose fine-grained information, while too fine a partition could negate the advantages of hierarchical processing. Furthermore, the choice of clustering algorithm itself can impact the effectiveness, with different methods exhibiting varying strengths and weaknesses concerning robustness to noise and efficiency.
Over-smoothing Reduction#
Over-smoothing, a critical problem in graph neural networks (GNNs), arises from the repeated propagation of node information, leading to feature homogenization. This paper addresses over-smoothing by employing a hierarchical cluster-based approach. Instead of globally propagating information across the entire graph, the encoding process decomposes the graph into isolated subgraphs. This prevents information from flowing between unrelated parts of the graph during convolution, thus mitigating over-smoothing. The decoder, using soft node assignment, reconstructs the original graph structure, further enhancing feature diversity and preventing information loss during the hierarchical encoding process. This strategy allows for the extraction of both local and global structural features, resulting in more effective graph representations for downstream tasks. The key innovation lies in confining graph convolutional operations to isolated subgraphs, dramatically reducing the extent of information propagation and consequently the over-smoothing phenomenon. The results demonstrate the effectiveness of this method in improving the performance of graph autoencoders and producing superior graph-level and node-level representations.
Loss Function Design#
Effective loss function design is crucial for training graph autoencoders (GAEs). A well-designed loss function should balance the reconstruction of graph structure and node features, preventing overemphasis on one aspect. The paper’s approach likely involves a composite loss, combining terms to address both graph-level and node-level information. Local loss terms might focus on individual subgraph reconstruction during the encoding process, while global loss terms address the overall graph reconstruction in the decoding stage. This hierarchical strategy is likely chosen to mitigate the over-smoothing problem commonly encountered in GNNs by constraining information propagation within subgraphs. The use of a regularization term is probable to further enhance generalization and prevent overfitting. Balancing the weights of local and global loss components is critical and will likely be determined empirically through experimentation. The choice of loss function also implicitly influences the type of downstream tasks the GAE will be effective for (node or graph classification). A sophisticated loss design could allow the model to perform well on multiple tasks simultaneously. The success of the method ultimately hinges on its capacity to learn meaningful representations that are effective for the chosen applications.
Future Research#
Future research directions stemming from this hierarchical cluster-based graph autoencoder (HC-GAE) could explore several promising avenues. Extending HC-GAE to handle dynamic graphs is crucial, as many real-world networks evolve over time. This would involve adapting the hard/soft node assignment strategies to account for changes in the graph structure. Investigating the impact of different clustering algorithms on the model’s performance is also important, as various algorithms might yield different subgraph structures and impact representation learning. Developing more sophisticated loss functions could further enhance the model’s ability to capture complex graph features. Incorporating techniques like graph neural attention mechanisms could improve the model’s capacity to focus on relevant structural information, possibly alleviating the over-smoothing problem. Finally, a thorough comparison with other state-of-the-art graph representation learning methods on a broader range of datasets would provide more conclusive evidence of HC-GAE’s effectiveness and identify its limitations more precisely.
More visual insights#
More on figures
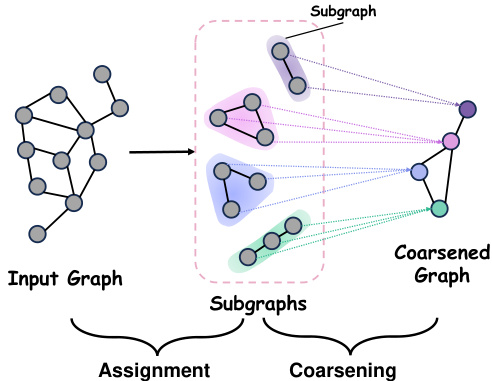
This figure illustrates the two main steps in the encoding process of the proposed HC-GAE model: hard node assignment and coarsening. First, the hard assignment step divides the input graph into several subgraphs. Then, the coarsening step compresses each subgraph into a single node, resulting in a smaller coarsened graph. This process is repeated layer-wise in the encoder to generate a sequence of progressively smaller graphs, extracting hierarchical structural features in the process.

This figure illustrates a single layer within the decoder of the proposed HC-GAE model. The decoder takes a retrieved graph (left) as input and aims to reconstruct the original graph structure by probabilistically expanding each coarsened node. The solid black lines represent the edges in the reconstructed graph, while the dotted pink and light blue lines represent the probabilistic expansion of nodes from the retrieved graph into the reconstructed graph. The process demonstrates the soft node assignment used in the HC-GAE decoder to probabilistically reconstruct the original graph structure.
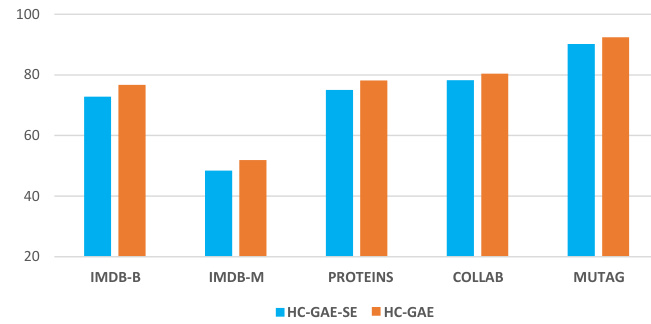
This figure shows the ablation study comparing the performance of the proposed HC-GAE model against a variant, HC-GAE-SE, which uses soft node assignment instead of hard node assignment in the encoder. The results across five graph classification datasets (IMDB-B, IMDB-M, PROTEINS, COLLAB, MUTAG) demonstrate that HC-GAE significantly outperforms HC-GAE-SE, highlighting the importance of hard node assignment for effective graph representation learning.
More on tables

This table presents the characteristics of five graph datasets used for graph classification experiments in the paper. For each dataset, it lists the number of graphs, the average number of nodes per graph, the average number of edges per graph, and the number of classes.
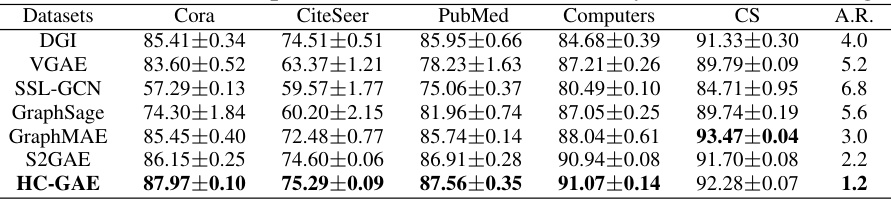
This table presents the node classification accuracy results for various models on five real-world datasets (Cora, CiteSeer, PubMed, Computers, and CS). The models compared include DGI, VGAE, SSL-GCN, GraphSage, GraphMAE, S2GAE, and the proposed HC-GAE. The accuracy is presented as mean ± standard deviation. The average rank (A.R.) across the datasets is also included to provide a summary comparison of model performance.
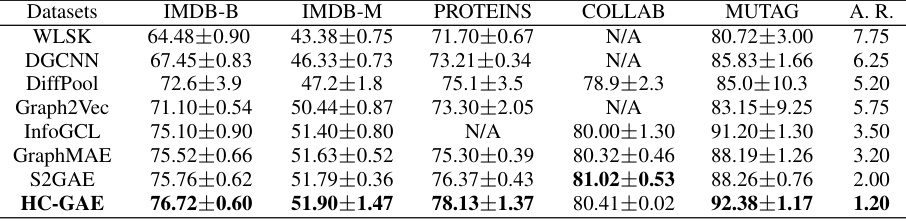
This table presents the results of graph classification experiments on five benchmark datasets (IMDB-B, IMDB-M, PROTEINS, COLLAB, MUTAG). It compares the accuracy of the proposed HC-GAE model against several baselines, including a graph kernel (WLSK), supervised GNNs (DGCNN, DiffPool), and other self-supervised GAEs (Graph2Vec, InfoGCL, GraphMAE, S2GAE). The average rank (A.R.) across datasets is also provided to summarize the relative performance of each method.
Full paper#


















