TL;DR#
Continual learning in graph data (GCL) faces the challenges of catastrophic forgetting and inter-task class separation, particularly in class-incremental learning scenarios where task IDs are unavailable during inference. Existing methods often struggle with these issues, leading to degraded performance. This paper focuses on Graph Class-Incremental Learning (GCIL), where the goal is to learn a sequence of tasks, each with unique classes, from graph data without using task IDs during inference. This is challenging because the model needs to separate classes from different tasks while remembering previous information, avoiding catastrophic forgetting.
This research proposes a novel Task Profiling and Prompting (TPP) approach to address these challenges. The method introduces a task profiling technique based on Laplacian smoothing to accurately predict the task ID of a test sample. This helps to isolate the classification space for each task, eliminating inter-task class separation. To avoid catastrophic forgetting, the TPP approach learns a small, task-specific graph prompt for each task, effectively creating separate classification models for each task without requiring data replay. Experiments demonstrate that TPP achieves 100% task ID prediction accuracy and significantly outperforms state-of-the-art methods by at least 18% in average accuracy across four benchmark datasets. Importantly, TPP is completely forget-free.
Key Takeaways#
Why does it matter?#
This paper is highly important for researchers working on graph continual learning (GCL), particularly in the challenging setting of class-incremental learning. It addresses the critical issue of catastrophic forgetting and inter-task class separation, offering a novel and effective solution that surpasses existing methods. The proposed task profiling and prompting approach has broad applications in various domains and significantly improves GCL model performance. The theoretical analysis and empirical validation of the method provide a solid foundation for future research in this area, opening up new avenues for tackling the challenges of continual learning in complex graph data structures.
Visual Insights#
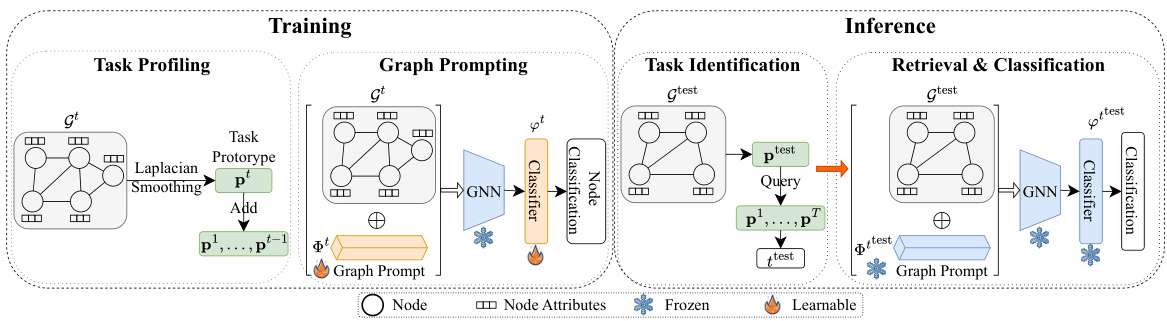
🔼 This figure illustrates the training and inference processes of the proposed Task Profiling and Prompting (TPP) approach for Graph Class-Incremental Learning (GCIL). During training, a task prototype is generated for each task using Laplacian smoothing, and a task-specific graph prompt is learned using a pre-trained GNN. The GNN remains frozen after initial training. During inference, the task ID is predicted using the task prototypes and the corresponding graph prompt and classifier are retrieved to classify nodes in the test graph.
read the caption
Figure 2: Overview of the proposed TPP approach. During training, for each graph task t, the task prototype pt is generated by applying Laplacian smoothing on the graph Gt and added to P = {p¹, ..., pt-1}. At the same time, the graph prompt It and the classification head φt for this task are optimized on Gt through a frozen pre-trained GNN. During inference, the task ID of the test graph is first inferred (i.e., task identification). Then, the graph prompt and the classifier of the predicted task are retrieved to perform the node classification in GCIL. The GNN is trained on G1 and remains frozen for subsequent tasks.

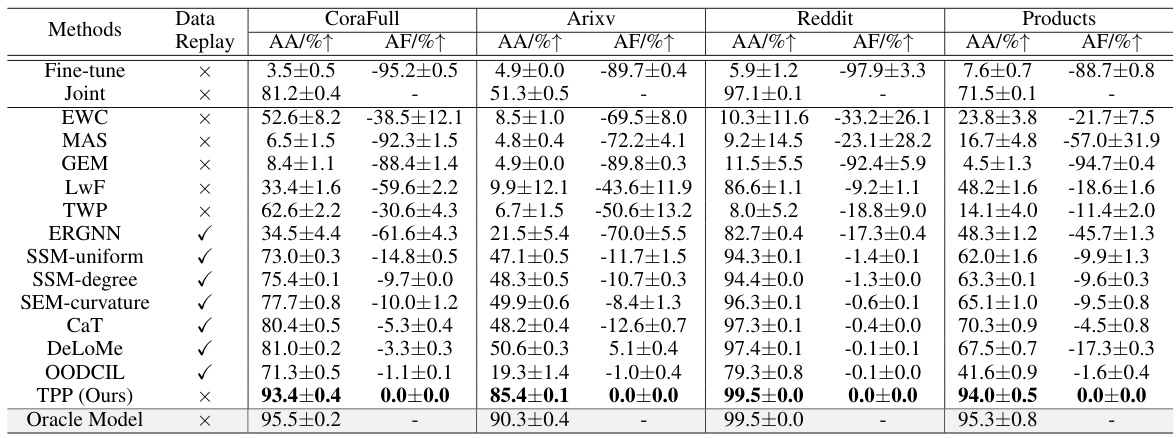
🔼 This table presents the results of different continual learning methods on four large graph datasets under the graph class-incremental learning (GCIL) setting. It compares the average accuracy (AA) and average forgetting (AF) of various methods, including baseline methods (Fine-tune, Joint), regularization-based methods (EWC, MAS, GEM, LwF, TWP), and replay-based methods (ERGNN, SSM-uniform, SSM-degree, SEM-curvature, CaT, DeLoMe, OODCIL). The results are shown with standard deviations and highlight the best performance for each dataset. An Oracle Model (with access to all data and task IDs) provides an upper bound. The table also shows whether each method utilizes data replay or not.
read the caption
Table 1: Results (mean±std) under the GCIL setting on four large datasets. The best performance on each dataset is boldfaced. “↑” denotes the higher value represents better performance. Oracle Model can get access to the data of all tasks and task IDs, i.e., it obtains the upper bound performance. “√” in Data Replay indicates the use of data replay in the model, and × denotes no data replay involved.
In-depth insights#
Graph Task Profiling#
The concept of ‘Graph Task Profiling’ in the context of graph class-incremental learning (GCIL) is a crucial innovation. It addresses the challenge of task identification in scenarios where task labels are absent during inference. The core idea involves representing each task as a prototypical embedding derived from its associated graph data, effectively creating a profile for each distinct task. This profiling leverages the graph’s structure and node attributes, often via a Laplacian smoothing technique. Laplacian smoothing is particularly insightful because it highlights the underlying relationships within each graph, making the task prototypes more robust and discriminative. The effectiveness of this method relies on the assumption that graphs from the same task exhibit similar structural and attribute properties, leading to closely clustered prototypes, while prototypes from different tasks remain well-separated. This, in essence, translates the problem of inter-task class separation into a similarity-based task identification problem, which can be solved efficiently using distance metrics like Euclidean distance. The success of task profiling critically enhances GCIL by enabling more accurate class predictions, confining the classification to the correct task’s classes and thereby circumventing the confusion caused by overlapping classes from different tasks. The strength of this approach is its ability to leverage graph-specific information, surpassing methods based on feature representations alone.
Prompting Approach#
The described prompting approach offers a novel way to address catastrophic forgetting in graph class-incremental learning (GCIL). Instead of relying on memory mechanisms or parameter regularization, it utilizes task-specific graph prompts. These prompts, learned for each task using a frozen pre-trained Graph Neural Network (GNN), act as small, learnable additions to the input graph, effectively creating task-specific sub-models without requiring extensive parameter updates or data replays. This replay-free and forget-free characteristic is a significant advantage, as it avoids the computational overhead and potential information loss associated with traditional continual learning techniques. The method’s effectiveness stems from its ability to isolate the knowledge of each task within its corresponding prompt. This approach leverages the GNN’s inherent ability to handle non-Euclidean graph data. The key to this success is the seamless combination of accurate task identification through Laplacian-based smoothing with the prompt-based model fine-tuning. This combination provides an effective strategy for achieving high accuracy and preventing catastrophic forgetting simultaneously in GCIL tasks.
Replay-Free GCIL#
Replay-free GCIL (Graph Class-Incremental Learning) represents a significant advancement in continual learning. Traditional GCIL methods often rely on data replay, storing and revisiting past data to mitigate catastrophic forgetting – the phenomenon where learning new tasks causes the model to forget previously learned ones. Replay-free approaches eliminate this need, leading to reduced memory requirements and computational cost. However, achieving replay-free GCIL presents unique challenges, particularly in maintaining the ability to distinguish between classes from different tasks without the benefit of task identifiers or past data. This necessitates novel techniques to ensure adequate class separation and prevent forgetting. Methods that successfully achieve this typically incorporate mechanisms such as task-specific prompts or parameter isolation, ensuring the model maintains and applies previously learned knowledge to new tasks without relying on revisiting previous data. The focus is on developing effective techniques that enable the model to effectively leverage implicit information for better task discrimination. This research area is crucial for real-world deployment, where memory and computational resources are limited and continual adaptation is necessary.
Forget-Free GCIL#
Forget-Free GCIL (Graph Class-Incremental Learning) tackles a critical challenge in continual learning: catastrophic forgetting. Traditional GCIL methods struggle to learn new graph tasks without losing knowledge from previous ones. A forget-free approach aims to address this by ensuring that the model retains all previously learned information. This is achieved through techniques such as parameter isolation, regularization, or memory replay. However, these often introduce complexity and/or performance trade-offs. A truly forget-free GCIL model would represent a significant advancement, enabling robust and efficient lifelong learning for complex graph data. The key to success lies in designing architectures and training strategies that allow for incremental learning while preserving all past knowledge, potentially using novel approaches such as task-specific prompts or specialized memory modules capable of retaining task-specific features without interference. Achieving a completely forget-free system presents substantial challenges but offers a transformative potential for various applications relying on graph-structured data.
Future of GCIL#
The future of Graph Class-Incremental Learning (GCIL) hinges on addressing current limitations and exploring novel approaches. Improving task identification accuracy is crucial; current methods struggle with noisy or ambiguous graph data. This requires advancements in graph representation learning and potentially incorporating external knowledge sources. Developing more robust and efficient methods for handling catastrophic forgetting is another key area. While prompting shows promise, research should focus on developing more sophisticated methods that prevent knowledge degradation across tasks without relying on extensive data replay. Further exploration of transfer learning techniques to leverage knowledge from previously learned tasks is warranted. This could involve pre-training models on large-scale graph datasets and fine-tuning them for specific GCIL tasks. Finally, the development of more comprehensive benchmark datasets is needed to ensure fair evaluation and drive progress in the field. These datasets should capture the diversity and complexity of real-world graph data while considering various factors like graph size, node features, edge structure, and class distribution.
More visual insights#
More on figures
🔼 This figure illustrates the effect of task ID prediction and graph prompting on the classification space of two graph tasks. (a) shows the overlapping classification spaces when task IDs aren’t provided. (b) and (c) demonstrate how accurate task ID prediction separates the classification spaces. (d) and (e) show how graph prompting further improves class separation within each task, effectively creating separate classification models and mitigating catastrophic forgetting.
read the caption
Figure 1: (a) Classification space of two graph tasks when no task ID is provided. The classification space is split into two separate spaces in Task 1 in (b) and Task 2 in (c) when the task ID can be accurately predicted. This helps alleviate the inter-task class separation issue. To mitigate catastrophic forgetting, we learn a graph prompt for each task that absorbs task-specific discriminative information for better class separation within each task, as shown in (d) and (e) respectively. This essentially results in a separate classification model for each task, achieving fully forget-free GCIL models.

🔼 This figure illustrates the impact of task ID prediction and graph prompting on the classification space in graph class-incremental learning (GCIL). (a) shows overlapping classes from two tasks without task IDs. (b) and (c) show the separated classification spaces when accurate task ID prediction is used. (d) and (e) demonstrate the effect of graph prompting in further separating classes within each task, resulting in forget-free learning.
read the caption
Figure 1: (a) Classification space of two graph tasks when no task ID is provided. The classification space is split into two separate spaces in Task 1 in (b) and Task 2 in (c) when the task ID can be accurately predicted. This helps alleviate the inter-task class separation issue. To mitigate catastrophic forgetting, we learn a graph prompt for each task that absorbs task-specific discriminative information for better class separation within each task, as shown in (d) and (e) respectively. This essentially results in a separate classification model for each task, achieving fully forget-free GCIL models.
More on tables
🔼 This table presents the results of various continual learning methods on four graph datasets under the graph class-incremental learning (GCIL) setting. The methods are evaluated based on average accuracy (AA) and average forgetting (AF). A comparison is made with a fine-tuning baseline, a joint training baseline (which has access to all data), and an oracle model (which also knows the task IDs). The table shows the performance of each method, indicating whether data replay was used and highlighting the best performance for each dataset.
read the caption
Table 1: Results (mean±std) under the GCIL setting on four large datasets. The best performance on each dataset is boldfaced. “↑” denotes the higher value represents better performance. Oracle Model can get access to the data of all tasks and task IDs, i.e., it obtains the upper bound performance. “√” in Data Replay indicates the use of data replay in the model, and × denotes no data replay involved.

🔼 This table shows the average accuracy (AA) and average forgetting (AF) results of several existing graph class-incremental learning (GCIL) methods. It compares their performance when used alone versus when combined with the proposed task ID prediction method (TP). The results demonstrate the significant improvement in both AA and AF achieved by incorporating the task ID prediction module, highlighting its effectiveness in addressing the inter-task class separation problem common in GCIL.
read the caption
Table 2: AA and AF results of enabling existing GCIL methods with our task ID prediction (TP).

🔼 This table presents the ablation study results of the Task Profiling and Prompting (TPP) approach. It shows the average accuracy (AA) and average forgetting (AF) results across four datasets (CoraFull, Arxiv, Reddit, Products) when different components of TPP (Task ID prediction, graph prompting: prompt and classification head) are removed. The results highlight the contribution of each component to the overall performance of the method. For instance, it demonstrates the significant improvement in performance due to the inclusion of both Task ID prediction and graph prompting.
read the caption
Table 3: Results of TPP and its variants on ablating task ID prediction and graph prompting modules.
🔼 This table presents a comparison of different continual graph learning methods under the graph class-incremental learning (GCIL) setting on four large benchmark datasets (CoraFull, Arxiv, Reddit, Products). The results are reported as mean ± standard deviation of average accuracy (AA) and average forgetting (AF) across multiple runs. Methods are evaluated based on their average accuracy (AA) and the percentage of forgetting (AF) across all tasks. An Oracle model (which has access to all data and task IDs) provides an upper performance bound. The use of data replay for each method is indicated, with ‘×’ signifying that no replay was used.
read the caption
Table 1: Results (mean±std) under the GCIL setting on four large datasets. The best performance on each dataset is boldfaced. “↑” denotes the higher value represents better performance. Oracle Model can get access to the data of all tasks and task IDs, i.e., it obtains the upper bound performance. “√” in Data Replay indicates the use of data replay in the model, and × denotes no data replay involved.

🔼 This table presents the results of different continual learning methods on four graph datasets under the graph class-incremental learning (GCIL) setting. The table compares the average accuracy (AA) and average forgetting (AF) of various methods, including both general CIL methods and graph-specific CIL methods. It also shows the performance of an oracle model which has access to all data and task IDs, and indicates whether each method uses data replay. The best performing method for each dataset is highlighted.
read the caption
Table 1: Results (mean±std) under the GCIL setting on four large datasets. The best performance on each dataset is boldfaced. “↑” denotes the higher value represents better performance. Oracle Model can get access to the data of all tasks and task IDs, i.e., it obtains the upper bound performance. “√” in Data Replay indicates the use of data replay in the model, and × denotes no data replay involved.

🔼 This table presents the results of different continual graph learning methods on four benchmark datasets under the graph class-incremental learning (GCIL) setting. It compares the average accuracy (AA) and average forgetting (AF) of various methods, including several state-of-the-art (SOTA) methods. An Oracle Model that has access to all task data and IDs is included as an upper bound performance. The table also indicates whether each method uses data replay.
read the caption
Table 1: Results (mean±std) under the GCIL setting on four large datasets. The best performance on each dataset is boldfaced. “↑” denotes the higher value represents better performance. Oracle Model can get access to the data of all tasks and task IDs, i.e., it obtains the upper bound performance. “√” in Data Replay indicates the use of data replay in the model, and × denotes no data replay involved.
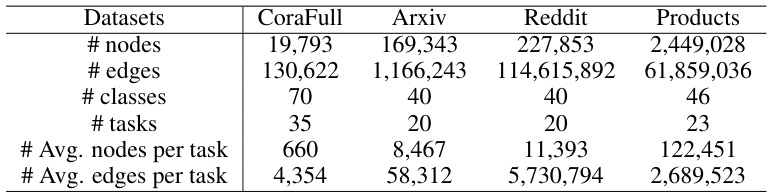
🔼 This table presents the average accuracy (AA) and average forgetting (AF) results for various graph continual learning methods on four benchmark datasets under the graph class-incremental learning (GCIL) setting. The results are shown for several state-of-the-art methods, along with two baseline methods (Fine-tune and Joint), and an Oracle model (which has access to all data and task IDs). The table highlights the best-performing method for each dataset and indicates whether data replay was used for each method. The metrics AA and AF are used to evaluate the performance and forgetting of these methods. A higher AA indicates better overall performance, while an AF of 0 indicates no forgetting.
read the caption
Table 1: Results (mean±std) under the GCIL setting on four large datasets. The best performance on each dataset is boldfaced. “↑” denotes the higher value represents better performance. Oracle Model can get access to the data of all tasks and task IDs, i.e., it obtains the upper bound performance. “√” in Data Replay indicates the use of data replay in the model, and × denotes no data replay involved.

🔼 This table presents the accuracy of the task prediction method used in the paper under different task formulations. These formulations vary how the classes are assigned to different tasks (ascending, descending, and random order). The results show consistent high accuracy (100%) across all datasets regardless of the class ordering.
read the caption
Table 6: The accuracy of task prediction with other task formulations.

🔼 This table compares the proposed graph prompting approach with learning separate task-specific models. It shows the number of additional parameters required for each method and their average accuracy (AA) across four datasets. The graph prompting method requires significantly fewer parameters while achieving comparable performance to task-specific models, highlighting its efficiency and effectiveness.
read the caption
Table 7: Additional parameters and performance (AA%) of the proposed graph prompting and task-specific models.

🔼 This table presents the total training and inference times for four different graph continual learning methods on the CoraFull dataset. The methods compared are TWP, SSM, DeMoLe, and the proposed TPP method. The training time reflects the time taken to train the model across all tasks, and the inference time represents the time needed to process a single test sample. The results highlight the efficiency of the proposed TPP method in terms of training time, showing a significant reduction compared to other methods. The inference time is relatively consistent across all methods.
read the caption
Table 8: Total training time and inference time (seconds) for different methods on CoraFull.
Full paper#



















