↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph Neural Networks (GNNs) are powerful tools for graph-level prediction tasks but their complex nature makes interpreting their predictions challenging. Existing GNN explainers mostly focus on local explanations, failing to reveal the global reasoning process. This lack of interpretability limits the trust and adoption of GNNs in sensitive application domains like healthcare and finance.
To tackle this, the paper introduces GRAPHTRAIL, a novel global explainer that translates GNN predictions into human-interpretable logical rules (boolean formulas). It achieves this by efficiently mining discriminative subgraph-level concepts using Shapley values and then employing symbolic regression to map GNN predictions to these concepts. Extensive experiments showcase that GRAPHTRAIL significantly outperforms existing global explainers in generating faithful and interpretable logical rules, making it a valuable tool for enhancing GNN understanding and deployment in diverse fields.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the critical need for interpretability in GNNs, a rapidly growing field with applications across many domains. By providing a method for translating complex GNN predictions into human-understandable rules, it enhances trust and facilitates adoption in high-stakes applications. The approach also opens up new avenues for research in GNN explainability and symbolic regression.
Visual Insights#

This figure presents a flowchart illustrating the different steps involved in the GRAPHTRAIL algorithm. It starts with input graphs and progresses through several stages: creation of computation trees (CTrees), canonization of these trees to identify unique ones, computation of Shapley values to rank these unique trees (indicating their importance in the GNN’s predictions), filtering of the less important trees, generation of concept vectors representing the selected trees, embedding those vectors, and finally, using symbolic regression to generate a logical formula that encapsulates the GNN’s decision-making process.
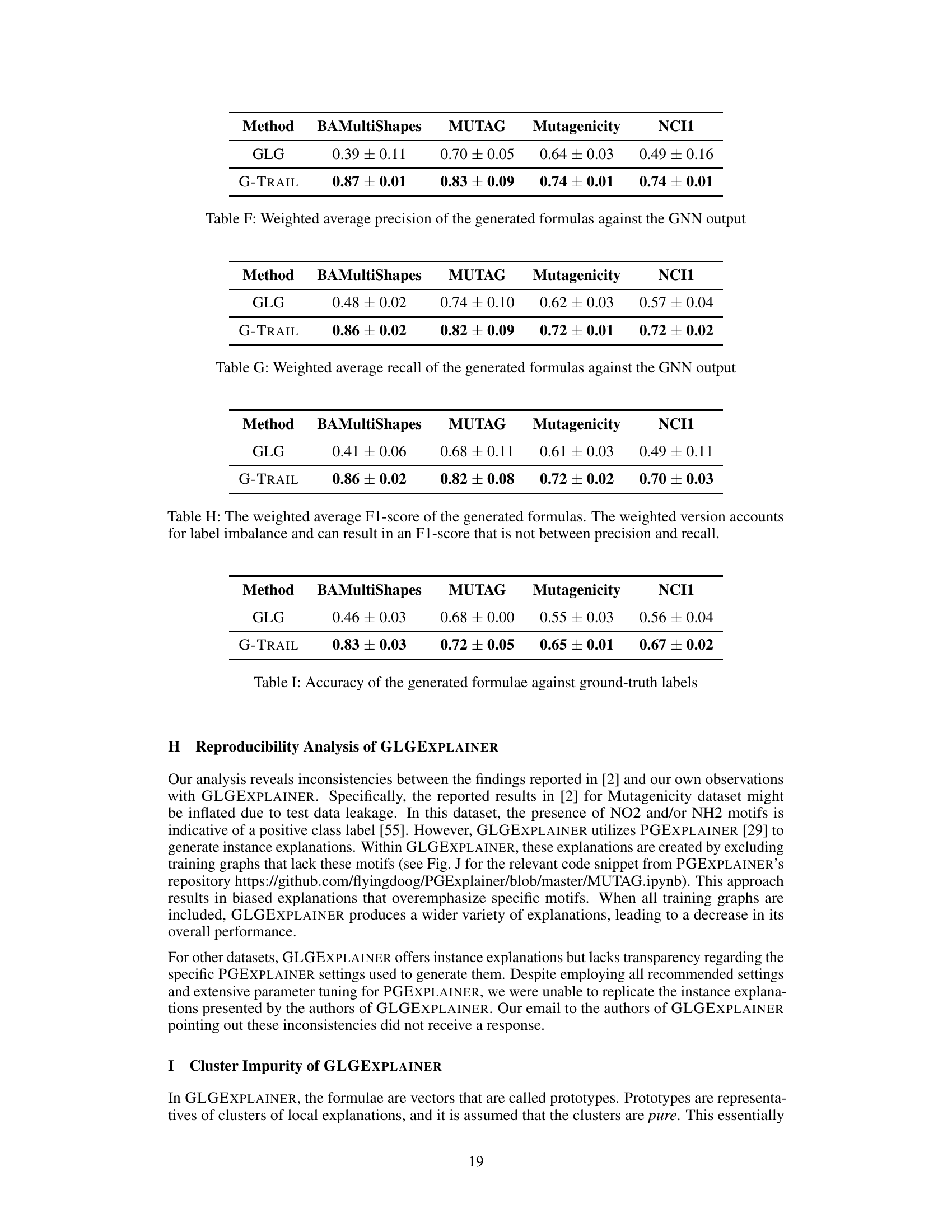
This table presents the average fidelity (faithfulness) of the boolean formulas generated by GRAPHTRAIL and its variant (GRAPHTRAIL-S), and the baseline method GLGEXPLAINER across three different random seeds. Fidelity is measured as the percentage of graphs where the generated logical formula correctly predicts the class label assigned by the GNN model. The results show that GRAPHTRAIL consistently outperforms GLGEXPLAINER in terms of fidelity.
In-depth insights#
GNN Explainability#
GNN explainability is a critical area of research because of the inherent complexity of Graph Neural Networks (GNNs). Understanding how GNNs arrive at their predictions is crucial for building trust, identifying potential biases, and improving model performance. Current approaches largely focus on either instance-level explanations, which offer insights into individual predictions but lack generalizability, or global explanations, which aim to capture the overall reasoning but may struggle with detailed interpretability. The ideal approach would combine the strengths of both, providing a high-level understanding while maintaining the granularity to explain specific decisions. Model-agnostic techniques are particularly attractive as they are not limited to specific GNN architectures. Furthermore, the development of human-interpretable explanations, such as logical rules or natural language descriptions, is vital to making GNNs accessible and beneficial to a wider range of users and applications, particularly in domains with high transparency requirements.
Boolean Logic#
The concept of Boolean logic, when applied to explain Graph Neural Network (GNN) predictions, offers a powerful mechanism for creating human-interpretable models. By representing GNN decision-making as a combination of subgraph features through Boolean operations (AND, OR, NOT, XOR), the complex internal processes of the GNN can be simplified. This approach makes it possible to understand which combinations of subgraph patterns are most influential in the GNN’s classification task and thereby gain insights into how the model arrives at its predictions. The use of Boolean logic facilitates the creation of easily understandable rules, promoting trust and facilitating the adoption of GNNs in high-stakes applications where explainability is paramount. A crucial advantage is the ability to translate complex GNN behavior into a simpler logical format, making it easier to identify and address potential biases or limitations in the model. However, effectively applying Boolean logic necessitates efficient methods for identifying key subgraph features and an optimized strategy for finding minimal Boolean expressions that accurately reflect the GNN’s behavior. This is a computationally complex task which might require carefully designed algorithms or the use of symbolic regression techniques. The effectiveness of this approach will largely depend on the complexity of the GNN and the underlying data, as well as the chosen algorithm for generating Boolean rules. Further research should explore more advanced Boolean logic representations to improve model accuracy while maintaining interpretability.
Shapley Values#
Shapley values, a solution concept in cooperative game theory, offer a powerful approach for explaining the predictions of complex models like Graph Neural Networks (GNNs). They provide a principled way to quantify the contribution of each feature or subgraph to the overall prediction, addressing the inherent black-box nature of GNNs. By considering all possible combinations of features, Shapley values avoid the shortcomings of local methods which only examine individual feature influences in isolation. This global perspective allows for a more comprehensive and robust understanding of model behavior, revealing synergistic interactions between subgraphs and providing insights into the decision-making process beyond individual component attributions. However, computing Shapley values for GNNs can be computationally expensive due to the exponential number of possible feature subsets. The GRAPHTRAIL paper cleverly addresses this challenge by leveraging the structure of message-passing GNNs, focusing on computation trees rather than all possible subgraphs, leading to significant computational gains. This innovative approach makes Shapley values a practical tool for explainability in the context of GNNs, opening pathways for enhanced model interpretability and trustworthiness.
Symbolic Regression#
Symbolic regression, in the context of the research paper, is a crucial technique for translating the complex internal workings of a Graph Neural Network (GNN) into a human-understandable form. The process involves discovering a concise mathematical equation—a logical formula—that accurately reflects the GNN’s predictive behavior. This is achieved by using a set of input-output pairs representing the GNN’s predictions on various graphs and a set of permitted mathematical operations. The goal is not just accurate prediction, but also to find a formula with minimal complexity, improving its interpretability. The challenge lies in the vast search space of possible formulae. The paper likely employs an evolutionary algorithm or other sophisticated optimization strategy to navigate this complexity and identify the best-fitting, yet concise, boolean expression. The boolean nature of the resulting formula is essential for creating a human-interpretable representation, as it aligns well with symbolic logic, making it easier for humans to grasp the decision-making process of the GNN. This approach is particularly valuable in applications demanding transparency and trust, such as healthcare or finance, where understanding the model’s reasoning is critical.
Future Directions#
The paper’s ‘Future Directions’ section could explore extending GRAPHTRAIL’s capabilities to handle more complex graph structures, such as directed or temporal graphs. Addressing limitations in handling very large graphs is crucial for broader applicability. Investigating the theoretical underpinnings of Shapley value approximations within the context of computation trees and symbolic regression is warranted. Improving the interpretability of the generated boolean formulas remains a key challenge, potentially through visualization techniques or more expressive logical languages. Finally, evaluating GRAPHTRAIL’s performance on a wider variety of GNN architectures and tasks, along with a comparative study against other state-of-the-art global explainers is needed to establish its robustness and generalizability. Further research on the interplay between human interpretability and model faithfulness will be essential to guide future developments in global GNN explainability.
More visual insights#
More on figures

This figure illustrates how computation trees are constructed in a message-passing GNN. Two example graphs G1 and G2 are shown, each with a node (v1 and u1 respectively) whose computation tree is constructed for L=2 layers. The computation tree for each node includes all paths of length up to L starting from the node. The key takeaway is that even if two nodes have non-isomorphic L-hop neighborhoods (subgraphs), their computation trees can still be isomorphic. This property is crucial to the efficiency of the GRAPHTRAIL method.

This figure shows how the test set fidelity of GRAPHTRAIL and GLGEXPLAINER changes with varying training data sizes. The x-axis represents the fraction of the training dataset used, while the y-axis shows the test fidelity (average over three seeds). The plot demonstrates the robustness and data efficiency of GRAPHTRAIL, maintaining higher fidelity even with smaller training datasets compared to GLGEXPLAINER.

This figure shows the test set fidelity of GraphTrail and GLGExplainer across different fractions of the training dataset for four datasets (BAMultiShapes, MUTAG, Mutagenicity, and NCI1). The x-axis represents the fraction of the training data used, and the y-axis shows the test fidelity. The figure demonstrates the robustness and stability of GRAPHTRAIL in low-data regimes, as its fidelity remains relatively high even with small fractions of the training data. Conversely, GLGExplainer shows a more significant decrease in fidelity as the amount of training data decreases.

This figure visually compares the logical rules (formulae) generated by GRAPHTRAIL and GLGExplainer for three different datasets: MUTAG, Mutagenicity, and BAMultiShapes. For each dataset, it shows the top-k computation trees (subgraphs) identified as important by each method, along with the resulting boolean formula and its fidelity (how accurately it reflects the GNN’s predictions). The figure highlights that GRAPHTRAIL produces more accurate and interpretable rules, especially in the Mutagenicity dataset, where it identifies key toxicophores related to mutagenicity, unlike GLGExplainer.

This figure presents a comprehensive taxonomy of existing GNN explanation methods. It categorizes them into instance-level and global-level explainers, further subdividing instance-level methods into gradients/features, decomposition, perturbation, and surrogate approaches. Each category lists specific algorithms with their corresponding references, indicating whether they are factual or counterfactual methods.

This figure illustrates how computation trees are constructed for a two-layered Graph Neural Network (GNN). Two example graphs G1 and G2 with nodes v1 and u1, respectively, are shown. Each node’s computation tree shows how information propagates through the graph within a two-hop radius. Despite the original graphs having non-isomorphic neighbourhoods around v1 and u1, the resulting computation trees are isomorphic. This illustrates a key concept in the GRAPHTRAIL algorithm; that isomorphic computation trees are collapsed into a single concept to reduce the number of concepts for efficient Boolean logic generation.
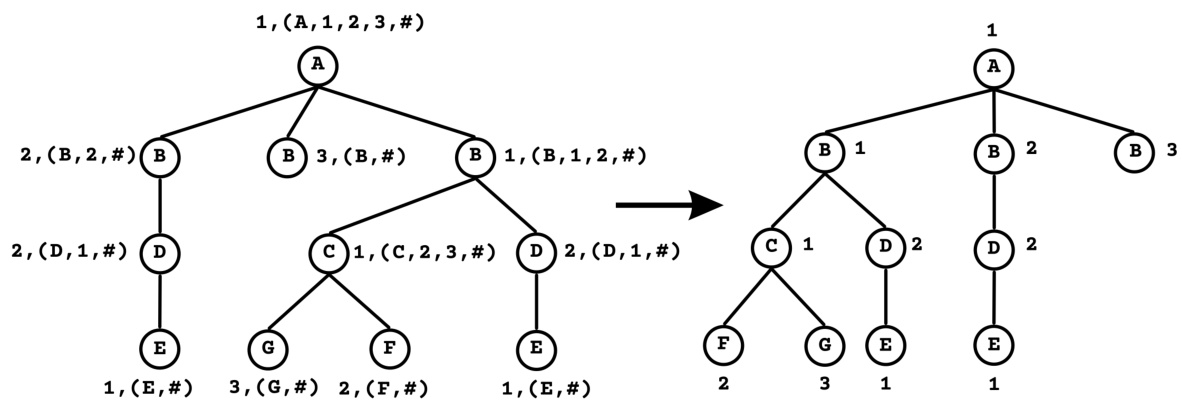
This figure illustrates the pipeline of the GRAPHTRAIL algorithm, which consists of several steps: 1) Graph and Computation Tree Extraction: the input graph is processed to extract computation trees, which capture the information flow within the GNN; 2) Canonization: computation trees are converted into a canonical form for efficient comparison and concept mining; 3) Shapley Value Computation: Shapley values are computed for each unique computation tree to identify the most important concepts in the GNN’s decision-making process; 4) Concept Vector Generation: concept vectors are created to represent the presence or absence of the selected concepts in each graph; 5) Symbolic Regression: a boolean formula is learned that maps the concept vectors to the GNN’s predictions. The resulting formula is human-interpretable and explains the GNN’s decision-making process at a global level.

The figure shows a flowchart of the GRAPHTRAIL algorithm. It starts with a graph and produces a logical formula. The main steps are: (1) canonization of computation trees (CTrees), (2) filtering based on Shapley values, (3) concept vector creation, (4) symbolic regression to get a logical formula.
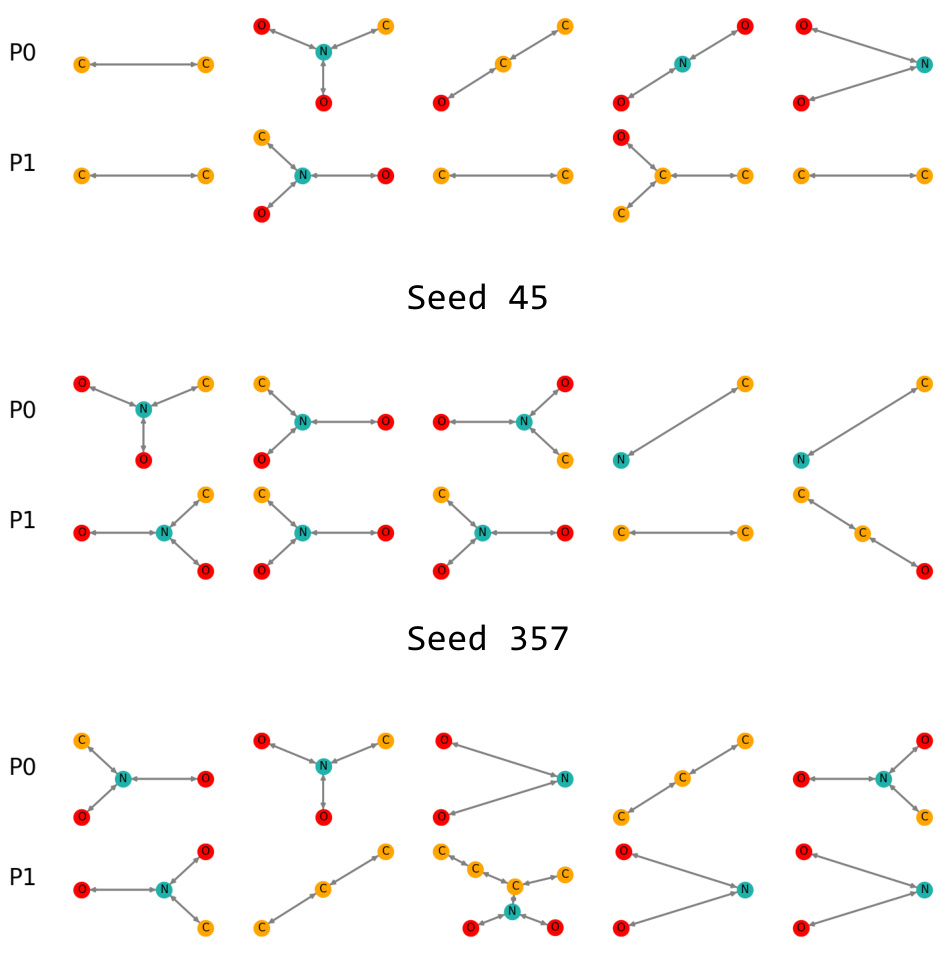
This figure visually demonstrates the impurity within the clusters generated by the GLGExplainer algorithm in the MUTAG dataset. It shows examples from different seeds (random starting points for the algorithm) to illustrate that the clusters contain diverse graph structures, rather than being homogeneous. This impurity contradicts the assumption in GLGExplainer that clusters are pure, and weakens the reliability of the method.

This figure visually shows the impure clusters generated by the GLGExplainer method in the MUTAG dataset. It demonstrates that the clusters produced by GLGExplainer are not pure; they contain graphs from different classes, indicating that the method’s cluster assignment does not effectively separate data points based on their class labels. This is shown for three different random seeds (45, 357, and 729), each illustrating the lack of purity within the generated clusters. The lack of purity in these clusters directly affects the interpretability and accuracy of the GLGExplainer’s logical formulas, which are built upon these clusters.
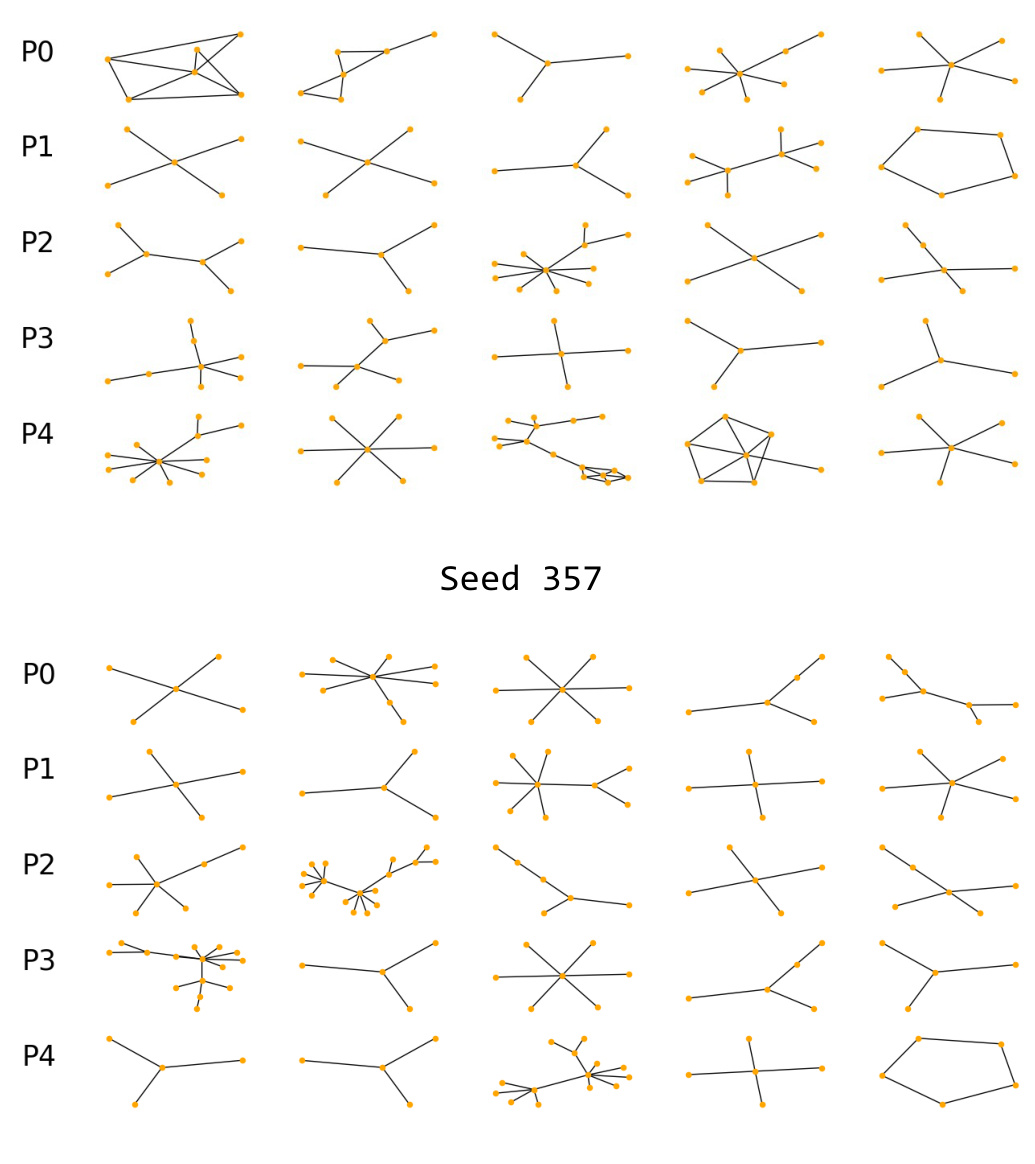
This figure visually demonstrates the impurity of clusters generated by the GLGExplainer method in the BAMultiShapes dataset. It shows examples of graphs from different clusters, highlighting the lack of homogeneity within each cluster. The lack of purity in these clusters is a significant limitation of the GLGExplainer approach, as it impacts the interpretability and reliability of its explanations.
The figure shows the pipeline of the GRAPHTRAIL algorithm. It starts with a graph as input. Then, the computation trees are extracted, and canonicalized. After filtering, the unique computation trees are used to compute the Shapley values. The top-k computation trees are then selected as concepts. These concepts are mapped to concept vectors and subsequently to their embeddings. Finally, these concept embeddings are used in a symbolic regression to obtain a logical formula.
More on tables

This table shows the fidelity (faithfulness) of the logical formulas generated by GRAPHTRAIL and GLGEXPLAINER across different Graph Neural Network (GNN) architectures (GCN, GAT, GIN) and pooling layers (SUM, MEAN, MAX). Higher fidelity indicates a better match between the GNN’s prediction and the formula’s prediction. The best fidelity score for each dataset and GNN architecture/pooling layer combination is shown in bold.

This table presents the average fidelity of the boolean formulas generated by GRAPHTRAIL and the baseline method GLGEXPLAINER across three different random seeds for four benchmark datasets. Fidelity is defined as the ratio of graphs where the logical formula matches the GNN class label. The best and second-best results for each dataset are highlighted in bold and underlined, respectively, to easily compare the performance of both methods.

This table presents the average fidelity (the ratio of graphs where the logical formula matches the GNN class label) achieved by three different methods (GRAPHTRAIL, GLGEXPLAINER, and a modified version of GLGEXPLAINER) across four different datasets. The best and second-best fidelities for each dataset are highlighted in bold and underlined, respectively. The results demonstrate the superior performance of GRAPHTRAIL in generating faithful logical formulas compared to the baselines.

This table presents the model accuracy for different graph neural network (GNN) architectures (GCN, GIN, GAT) and pooling layers (Sum, Mean, Max) used for aggregating node embeddings into a graph embedding. The accuracy is evaluated across four different datasets (BAMultiShapes, MUTAG, Mutagenicity, NCI1), providing a comprehensive assessment of the performance of various GNN configurations.

This table presents the average fidelity of the generated logical formulas across three different random seeds for four benchmark datasets (BAMultiShapes, MUTAG, Mutagenicity, NCI1) when using Shapley values to select computation trees versus selecting them randomly. The fidelity metric reflects the faithfulness of the logical formula in predicting the GNN’s classification. The results show that using Shapley values leads to significantly higher fidelity, indicating the importance of Shapley values in identifying the most relevant computation trees for explaining GNN predictions.

This table presents the average fidelity of the boolean formulas generated by GRAPHTRAIL and GLGEXPLAINER across three different random seeds. Fidelity is a metric that measures how well the logical formula matches the GNN’s predictions. Higher fidelity indicates better faithfulness of the formula. The table shows that GRAPHTRAIL achieves significantly higher fidelity than GLGEXPLAINER across all datasets, demonstrating its superior ability to capture the GNN’s decision-making logic.

This table presents the average fidelity of the boolean formulas generated by GRAPHTRAIL and the baseline GLGEXPLAINER across three different random seeds for four datasets. Fidelity is a measure of how well the generated formula matches the predictions of the GNN model. Higher fidelity indicates better agreement between the formula and the model’s predictions. The table highlights that GRAPHTRAIL consistently achieves higher fidelity than GLGEXPLAINER across all datasets.

This table presents the average fidelity achieved by GRAPHTRAIL and GLGEXPLAINER across three different random seeds for four datasets. Fidelity is defined as the ratio of graphs where the logical formula generated by the explainer matches the prediction of the black-box GNN model. The best and second-best fidelities are highlighted for easier comparison.

This table shows the average fidelity scores achieved by GRAPHTRAIL and its variant, along with the GLGEXPLAINER baseline, across three different seeds. Fidelity measures how often the logical formula generated by each method correctly matches the prediction of the GNN model. Higher fidelity indicates better agreement between the logical rules and the GNN’s predictions. The best and second-best results are highlighted to facilitate comparison.
Full paper#