Learning Plaintext-Ciphertext Cryptographic Problems via ANF-based SAT Instance Representation

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents CryptoANFNet, a novel approach to solving cryptographic problems using machine learning. It offers a 50x speedup over traditional methods and achieves higher accuracy, particularly on large-scale datasets. This opens up new avenues for research in learning-based cryptanalysis and could significantly advance the field.

Visual Insights

#

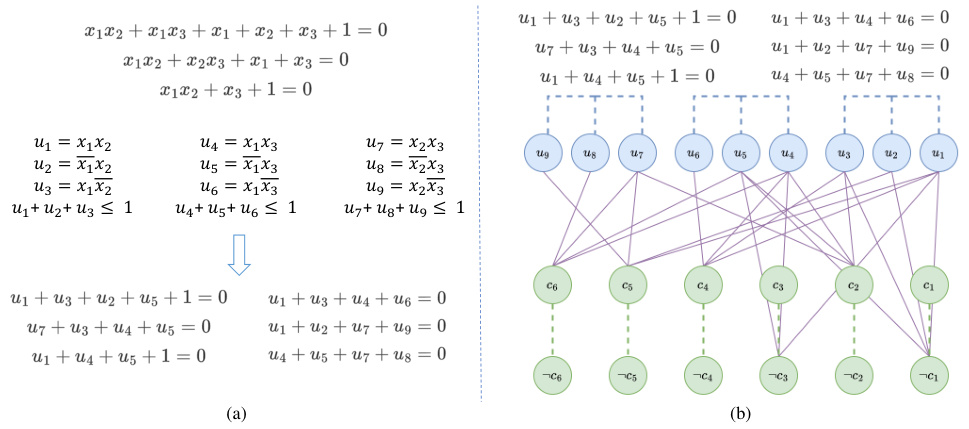
🔼 This figure illustrates two key aspects of the paper’s approach. (a) shows how an example multi-variate quadratic (MQ) problem is represented as a graph based on the algebraic normal form (ANF). This is a key contribution of the paper, showing how the ANF representation can be more efficient and effective than the traditional conjunctive normal form (CNF) in representing cryptographic problems for machine learning. (b) demonstrates how common operations in cryptography, like circular shifts, modular addition, XOR, and AND, can be transformed into their ANF equivalents, enabling their efficient encoding in the graph representation used by CryptoANFNet.

read the caption

Figure 1: (a) Example ANF formula graph from MQ problem; (b) The transformations to express the circular left shifts (≪), circular right shifts (≫), modular addition (田), bitwise XOR (+), and bitwise AND (·) operations in ANF.

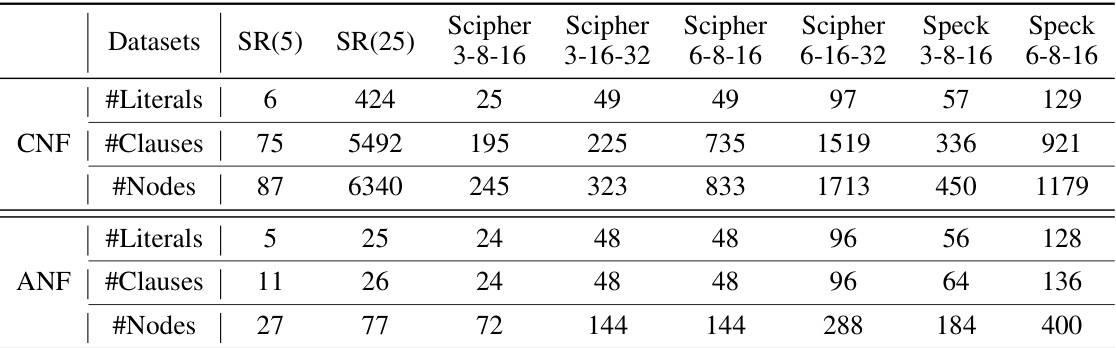
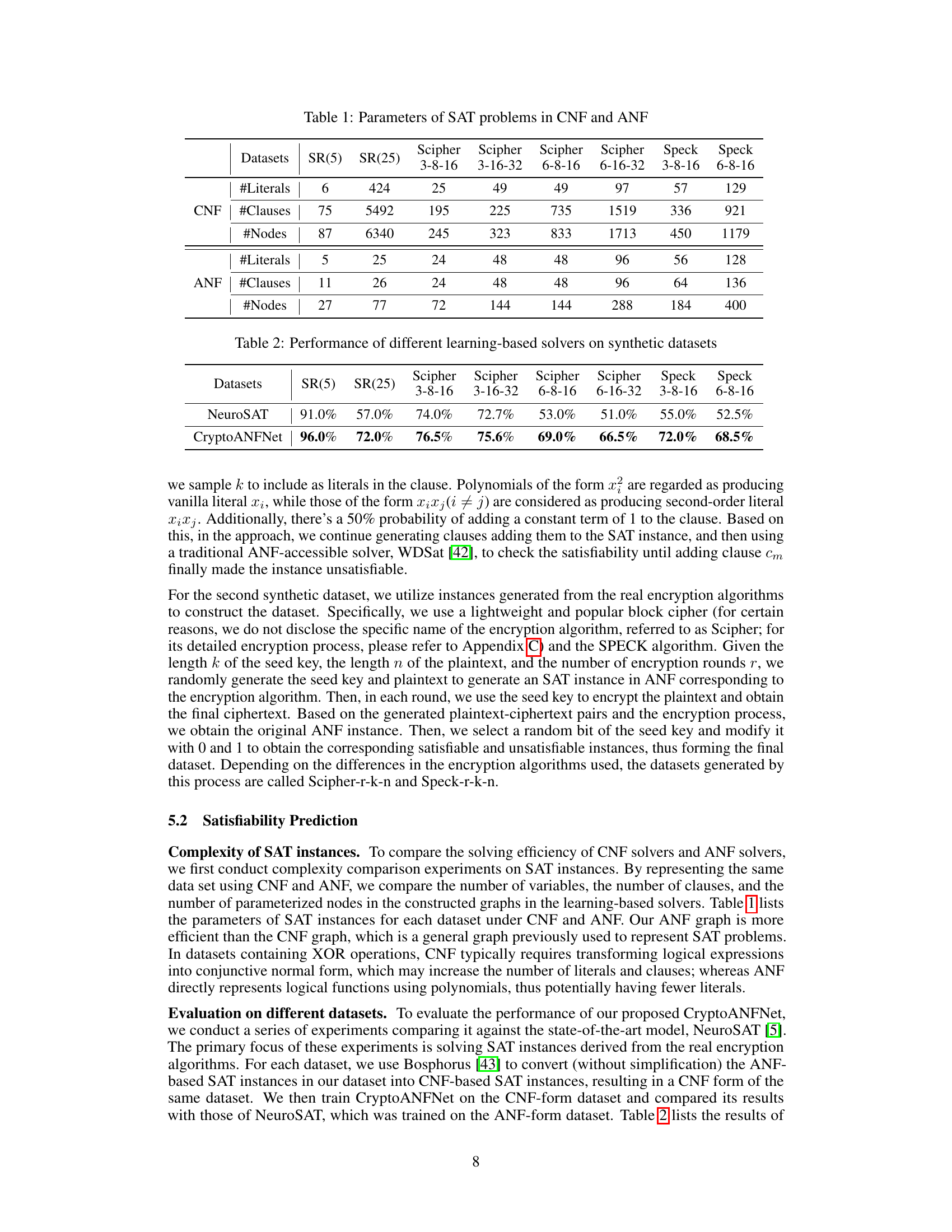
🔼 This table presents a comparison of the number of literals, clauses, and nodes in the CNF and ANF representations of SAT problems from different datasets. The datasets include synthetic datasets (SR(5), SR(25)), and datasets generated from real encryption algorithms (Scipher and Speck with varying parameters). It shows how the ANF representation leads to fewer nodes and a more efficient representation compared to CNF, especially beneficial for cryptographic problems with many XOR operations.

read the caption

Table 1: Parameters of SAT problems in CNF and ANF

In-depth insights

#

ANF-based SAT

#

The concept of “ANF-based SAT” presents a novel approach to encoding Boolean satisfiability problems, particularly beneficial for cryptographic applications. Arithmetic Normal Form (ANF) offers a more compact and efficient representation of Boolean functions compared to the traditional Conjunctive Normal Form (CNF), especially when dealing with the prevalent XOR operations in cryptography. By leveraging ANF, SAT instances can be represented with fewer clauses and variables, reducing the computational complexity of SAT solvers. This approach is particularly promising for large-scale cryptographic problems where CNF representation leads to an exponential blow-up. CryptoANFNet, a graph-based neural network model, directly takes advantage of this ANF-based representation, enabling efficient learning and prediction of plaintext-ciphertext satisfiability. The use of ANF graphs facilitates the capturing of higher-order operational information inherent in cryptographic algorithms, thus enhancing the model’s accuracy and scalability. Ultimately, ANF-based SAT offers a significant improvement over traditional CNF-based methods in handling the unique challenges presented by cryptographic problems.

CryptoANFNet

#

CryptoANFNet represents a novel graph neural network architecture designed for solving cryptographic problems. Its core innovation lies in leveraging the Arithmetic Normal Form (ANF) to represent Boolean formulas, offering a more efficient encoding compared to the traditional Conjunctive Normal Form (CNF). This efficiency is particularly beneficial when dealing with the XOR operations prevalent in cryptographic algorithms, as ANF avoids the exponential blow-up in clause numbers associated with CNF conversion of XORs. The ANF-based graph structure serves as input for CryptoANFNet, enabling it to naturally capture higher-order relationships within the cryptographic functions. By employing a message-passing scheme, the network learns effective representations for both literals and clauses. The model shows superior scalability and accuracy, outperforming existing learning-based SAT solvers. Its potential extends to key decryption problems through an auxiliary algorithm that leverages CryptoANFNet’s prediction capabilities to improve key-solving accuracy. Overall, CryptoANFNet demonstrates a significant advancement in the application of machine learning to cryptographic tasks.

Key Decryption

#

The concept of ‘Key Decryption’ within the context of cryptographic research is multifaceted and crucial. It implies the process of recovering a secret key used in encryption, enabling access to the original plaintext from its ciphertext. The paper likely explores techniques for efficient key decryption, perhaps focusing on the utilization of machine learning models, such as neural networks. The efficiency and accuracy of this decryption method are paramount, especially when dealing with large-scale datasets or complex encryption algorithms. The approach may involve transforming the problem into a suitable format, such as a Boolean Satisfiability (SAT) instance, which is then processed by the machine learning model. Novel algorithms or improved model architectures could be a core component of the discussed method. The success of the ‘Key Decryption’ process may be evaluated based on metrics such as the accuracy of key recovery and speed of computation. The trade-off between efficiency and accuracy is a key aspect to consider. Furthermore, the paper likely addresses the security implications of the proposed methods and discusses potential vulnerabilities or attacks.

Scalability & Speed

#

The research paper’s focus on scalability and speed is crucial for practical applications in cryptography. CryptoANFNet, the proposed model, demonstrates significant improvements over existing methods. A 50x speedup compared to traditional heuristic solvers highlights its efficiency. The utilization of Arithmetic Normal Form (ANF) instead of Conjunctive Normal Form (CNF) is key to this improvement, reducing the computational complexity associated with the XOR operations prevalent in cryptographic algorithms. This demonstrates that ANF-based representations offer a more compact and efficient encoding of cryptographic problems. The approach’s effectiveness on large-scale datasets underscores its suitability for real-world scenarios, suggesting that learning-based approaches are viable for addressing complex cryptographic tasks, previously intractable due to computational limitations. This scalability is vital for tackling more complex cryptographic challenges in the future.

Future Work

#

The paper’s ‘Future Work’ section could explore several promising avenues. Extending CryptoANFNet’s capabilities to handle more complex cryptographic problems beyond MQ instances is crucial. This might involve adapting the ANF graph representation and message-passing scheme to accommodate operations commonly found in asymmetric ciphers. Investigating the impact of different graph structures and neural network architectures on the model’s performance could yield significant improvements. Exploring alternative encoding schemes for ANF formulas and experimenting with graph neural networks beyond the message-passing approach could reveal more efficient and accurate methods. Furthermore, a detailed comparison with other learning-based SAT solvers is warranted, focusing not just on accuracy but also efficiency across diverse datasets. Finally, developing robust methods for handling noisy or incomplete data is essential for real-world applicability. This may involve incorporating techniques from robust optimization and leveraging the strengths of ensemble methods.

More visual insights

#

More on figures

🔼 This figure illustrates the key-solving algorithm’s workflow. It starts with a plaintext-ciphertext pair and the encryption algorithm. These are used to generate an Arithmetic Normal Form (ANF) representation of the problem. Then, for each bit in the key, two versions of the ANF are created: one assuming the bit is 0 and one assuming it is 1. These ANFs are fed into CryptoANFNet, which predicts their satisfiability. The bit’s value is decided by which ANF gets a higher satisfiability score.

read the caption

Figure 2: The pipeline of the key-solving algorithm. Given a plaintext-ciphertext pair and an encryption algorithm, we first transform them into an ANF-based instance of an MQ problem. Then, for a specific key bit Ki (the i-th bit of key), we guess its value as either 0 or 1 and generate two derived SAT instances. We then employ CryptoANFNet to predict the satisfiability of each instance. The final determination of Ki is based on which instance receives a higher satisfiability score.

🔼 This figure illustrates two ways to represent ANF formulas as graphs. (a) Shows how to transform an ANF formula with AND operations into an equivalent ANF formula without them by introducing new variables (U1, U2, etc.) and additional constraints to maintain the logical equivalence. (b) Presents a graph representation focusing only on second-order literals (terms with two variables multiplied together). This representation simplifies the graph by treating second-order literals as new, independent literals. Both illustrate different strategies for constructing ANF-based graphs for improved learning efficiency within the CryptoANFNet model.

read the caption

Figure 3: (a) A example ANF formula for changing the original ANF formula to a formula without AND operation; (b) Example ANF formula graph focusing on second-order literals

More on tables

🔼 This table compares the performance of two learning-based SAT solvers, NeuroSAT and CryptoANFNet, on various synthetic datasets. The datasets include SR(5), SR(25), and instances derived from the Scipher and Speck encryption algorithms with varying parameters. The results show CryptoANFNet achieving higher accuracy than NeuroSAT across all datasets, particularly on larger and more complex ones.

read the caption

Table 2: Performance of different learning-based solvers on synthetic datasets

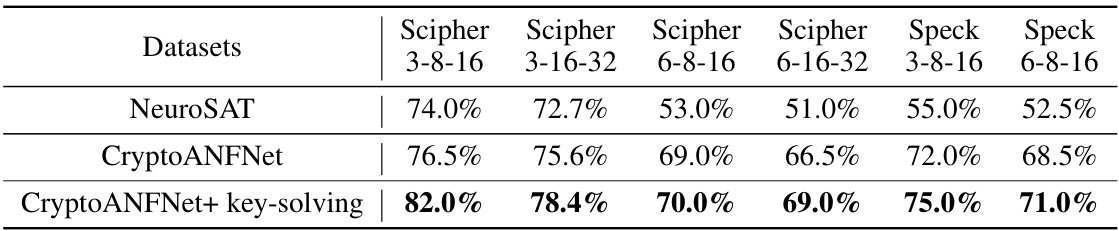
🔼 This table presents the performance comparison of NeuroSAT and CryptoANFNet, with and without the key-solving algorithm, on several synthetic datasets generated from two real encryption algorithms (Scipher and Speck). The results show the accuracy of each method in solving the MQ problems (key decryption) for different dataset sizes and parameters, demonstrating the effectiveness of the proposed key-solving algorithm in improving the accuracy of key decryption.

read the caption

Table 3: Performance for key-solving algorithm in solving MQ problems on synthetic datasets.

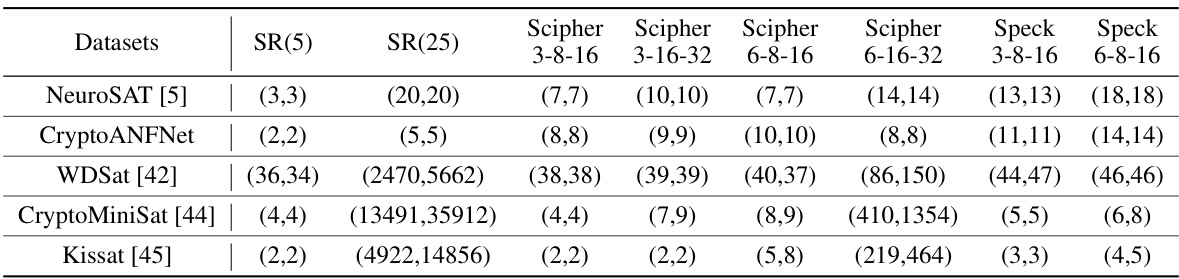
🔼 This table compares the performance of CryptoANFNet against the state-of-the-art learning-based SAT solver, NeuroSAT, on synthetic datasets of different sizes. It shows the accuracy of each model on various datasets, including SR(5), SR(25), and datasets derived from Scipher and Speck encryption algorithms. The results demonstrate that CryptoANFNet outperforms NeuroSAT on both small and large-scale datasets.

read the caption

Table 2: Performance of different learning-based solvers on synthetic datasets

🔼 This table compares the average runtime of three incomplete SAT solvers (WalkSAT, RoundingSAT, and FourierSAT) on various synthetic datasets. The datasets represent instances of the Multivariate Quadratic (MQ) problem, a common type of problem in cryptography. Runtimes are broken down into those for satisfiable (SAT) and unsatisfiable (UNSAT) instances, providing insight into solver performance depending on the instance’s properties. Different sizes and configurations of the MQ problem are included (indicated by ‘Scipher’ and ‘Speck’ variations and their parameter values).

read the caption

Table 5: Comparing the efficiency of incomplete solvers for solving the MQ problem on synthetic datasets. (Average runtime: (SAT, UNSAT) ms/instance)

Full paper

#