TL;DR#
Large language models (LLMs) have shown remarkable reasoning abilities, but challenges remain, including error accumulation in chain-of-thought prompting and computational inefficiency. Diffusion models offer potential advantages but have not been extensively explored for reasoning tasks. Prior work primarily uses autoregressive models that process information sequentially, potentially limiting efficiency and self-correction capabilities.
This paper proposes Diffusion-of-Thought (DoT), a novel method integrating diffusion models with chain-of-thought reasoning. DoT allows reasoning steps to diffuse over time in parallel, providing more flexibility in computational performance. Experimental results demonstrate DoT’s effectiveness in various reasoning tasks, surpassing larger autoregressive models in both efficiency and accuracy. DoT also showcases promising self-correction abilities, indicating significant potential for advancing complex reasoning in LLMs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large language models and diffusion models. It introduces a novel approach to enhance reasoning capabilities in diffusion models, an area currently receiving significant attention. The work’s findings on efficiency and accuracy improvements offer valuable insights and potentially open up new avenues for research in complex reasoning tasks.
Visual Insights#
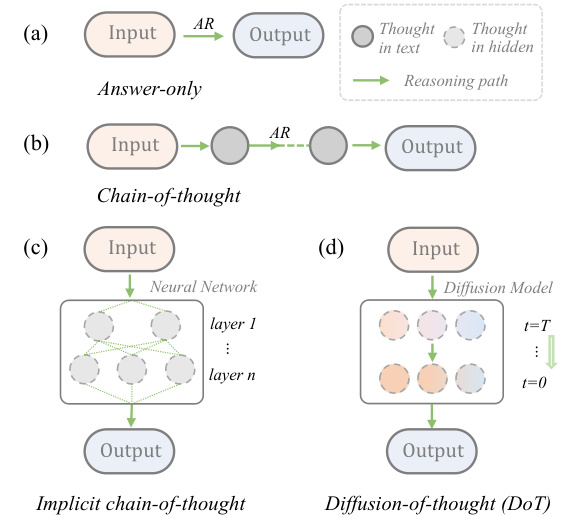
🔼 This figure illustrates four different reasoning approaches in language models. (a) shows the answer-only approach, where the model directly generates the answer without intermediate steps. (b) shows the chain-of-thought (CoT) approach, where the model generates a sequence of intermediate reasoning steps before producing the final answer. (c) shows the implicit CoT approach, where reasoning steps are implicitly learned within the layers of a neural network. (d) shows the Diffusion-of-Thought (DoT) approach proposed in the paper, which uses a diffusion model to generate reasoning steps over time. DoT leverages the diffusion process to allow for parallel reasoning steps and greater flexibility in balancing computation and performance.
read the caption
Figure 1: Illustration of reasoning approaches. (a) Answer-only and (b) CoT generate left-to-right tokens by prompting autoregressive language model. (c) Implicit CoT replaces horizontal reasoning (CoT) with vertical reasoning from shallow layer to deep layer [7]. (d) DoT generates reasoning path along with the diffusion timesteps.
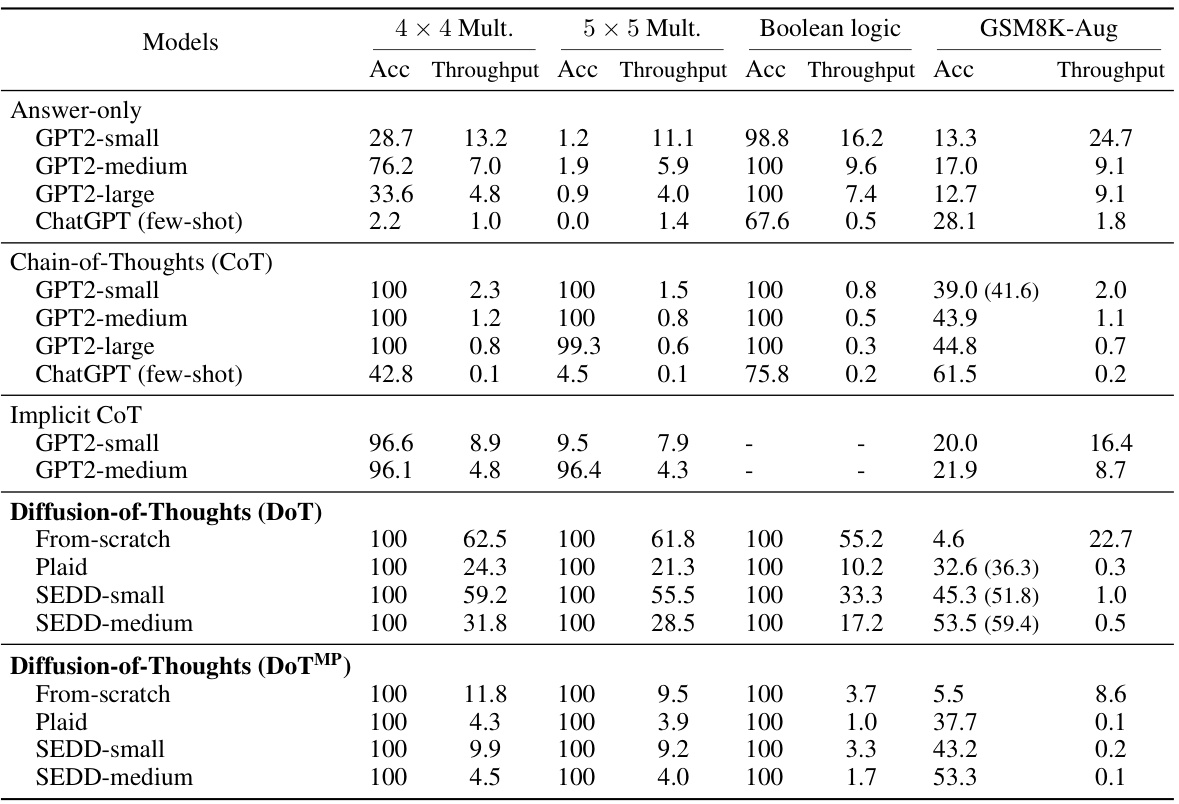
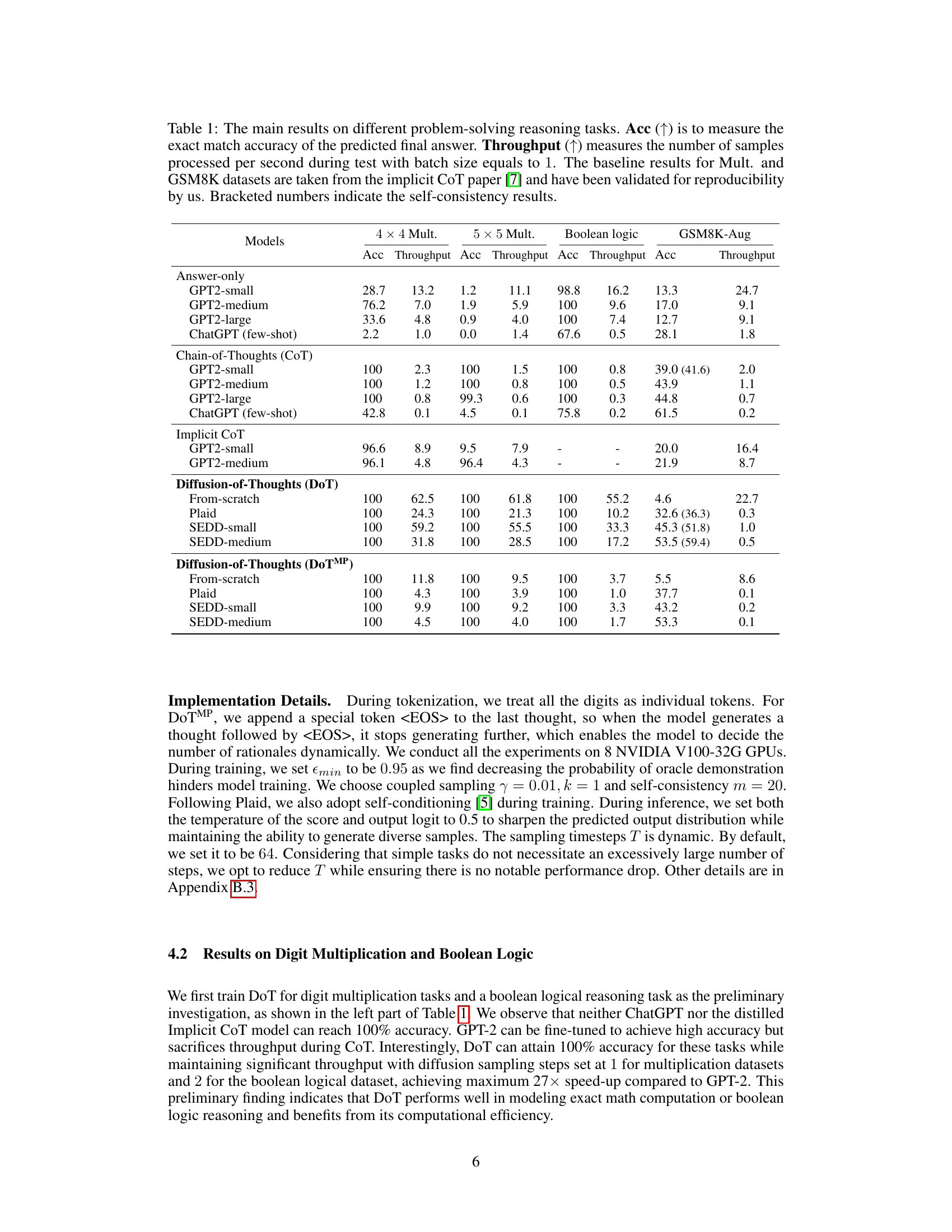
🔼 This table presents the main experimental results comparing various models on three reasoning tasks: 4x4 digit multiplication, 5x5 digit multiplication, boolean logic, and GSM8K (grade school math). For each task and model, it shows the accuracy and throughput. Accuracy represents the percentage of correctly solved problems, and throughput represents the number of problems solved per second. Baseline results from a previous study are included for comparison. Results in parentheses indicate performance when using self-consistency decoding. The table highlights the superior performance of the proposed Diffusion-of-Thought (DoT) method across different model sizes.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.
In-depth insights#
DoT Reasoning#
Diffusion of Thought (DoT) reasoning presents a novel approach to integrate diffusion models with chain-of-thought prompting. DoT’s core innovation lies in its ability to allow reasoning steps to diffuse over time, unlike the left-to-right processing of autoregressive models. This allows for parallel processing and flexibility in trading off computational cost for reasoning performance. The method demonstrates effectiveness across various tasks, particularly in mathematical problem-solving, showcasing an ability to outperform larger autoregressive models in both accuracy and efficiency. DoT also incorporates self-correction mechanisms and benefits from techniques like self-consistency decoding, indicating its potential to address limitations inherent in traditional chain-of-thought prompting. The inherent parallel nature of diffusion models may allow DoT to scale better to complex reasoning tasks than sequential methods.
Diffusion’s Edge#
The heading “Diffusion’s Edge” suggests an exploration of the advantages of diffusion models over other approaches, particularly in the context of natural language processing. A thoughtful analysis would delve into the specific strengths highlighted in the research paper. This might include superior performance on reasoning tasks, owing to diffusion’s inherent ability to explore the latent space more flexibly than autoregressive models. Self-correction mechanisms, potentially arising from the iterative nature of diffusion, would be another key point to analyze. The discussion should also assess the trade-offs, such as computational cost versus accuracy, and how these trade-offs might impact the overall practical applicability. Finally, comparing diffusion models to other leading language models, such as large language models (LLMs) that rely on autoregressive architectures and chain-of-thought prompting, is crucial to fully understand diffusion’s unique position and potential.
Multi-pass DoT#
The proposed Multi-pass Diffusion of Thought (DoT) method presents a refined approach to chain-of-thought reasoning within diffusion models. Instead of generating all reasoning steps concurrently, as in the single-pass DoT, Multi-pass DoT generates one reasoning step at a time. This sequential approach introduces a causal inductive bias, enabling each subsequent step to benefit from the context of previously generated steps, and reducing the accumulation of errors from earlier mistakes. This sequential generation also mitigates the potential for causal bias inherent in generating multiple steps in parallel, leading to more reliable and accurate solutions, especially in complex reasoning tasks. Furthermore, the multi-pass approach allows for more dynamic control over the reasoning process, potentially improving the trade-off between reasoning time and accuracy by tailoring the number of reasoning steps to the complexity of the problem. The integration of training-time sampling algorithms and self-consistency decoding further enhances its self-correction capabilities and robustness.
Self-Correction#
The concept of self-correction in AI models is crucial for reliable performance, especially in complex reasoning tasks. The paper explores self-correction within the framework of diffusion models, offering a unique perspective compared to traditional autoregressive approaches. Instead of relying solely on sequential, left-to-right generation, diffusion models’ inherent ability to diffuse information across time steps allows for a more holistic and iterative correction process. The authors introduce scheduled sampling during training to expose and correct errors arising from prior reasoning steps, mimicking the inference process. Further enhancing self-correction is the integration of coupled sampling in multi-pass DoT, which ensures robustness to errors in earlier stages. This multi-faceted approach, combining inherent diffusion properties with strategic training techniques, demonstrates improved self-correction capabilities in challenging mathematical reasoning problems. The results highlight the potential for diffusion models to overcome the error accumulation limitations frequently encountered in autoregressive models employing Chain-of-Thought prompting. This represents a significant step towards developing more reliable and robust reasoning systems.
Future DoT#
Future research directions for Diffusion-of-Thought (DoT) are promising. Improving efficiency remains crucial; current implementations are computationally expensive, limiting scalability. Exploring alternative diffusion models beyond Plaid and SEDD, including larger, more advanced models, could significantly enhance performance and reasoning capabilities. Addressing limitations in self-correction is key; while DoT shows promise, more robust mechanisms are needed to mitigate errors during reasoning. Incorporating advanced training techniques, such as reinforcement learning or curriculum learning, may lead to more effective and efficient training. Integrating DoT with other reasoning paradigms, such as chain-of-thought prompting and tree-of-thought, could create hybrid approaches with even greater power. Investigating applications to different tasks outside mathematical problem solving will demonstrate DoT’s broader applicability. Finally, addressing potential biases within diffusion models and mitigating their impact on generated reasoning steps is vital for responsible development.
More visual insights#
More on figures

🔼 This figure illustrates the Diffusion-of-Thoughts (DoT) pipeline. The single-pass DoT shows how reasoning steps diffuse over time through a diffusion model, updating a sequence of latent variables representing thoughts in parallel. The multi-pass DoT (DoTMP) method focuses on generating one thought at a time to address potential causal bias, improving accuracy by introducing causal inductive bias. The training process includes a ‘scheduled sampling’ mechanism to improve self-correction by exposing and correcting errors, and ‘coupled sampling’ to improve the robustness of multi-pass DoT. Finally, inference accelerates by utilizing a conditional ODE solver.
read the caption
Figure 2: Demonstration of DoT pipeline. DoT diffuses all possible thoughts across diffusion timestep t. Multi-pass DoT disentangles each rationale and introduces causal bias. The stacked circles stand for the marginalization over other potential reasoning paths, which is implicitly carried out during the training of diffusion models.

🔼 This figure shows how using an ODE solver improves the inference speed of the Plaid DoT model. The x-axis represents the number of timesteps (T) used during the sampling process, and the y-axis shows the accuracy achieved. Multiple lines are presented, comparing the performance of DoT and DoTMP models both with and without the ODE solver. The results demonstrate that incorporating the ODE solver significantly accelerates inference without sacrificing accuracy, highlighting its beneficial impact on the efficiency of the DoT approach.
read the caption
Figure 3: The effectiveness of ODE solver in speedup inference of Plaid DoT.
🔼 This figure illustrates the pipeline of the proposed Diffusion of Thought (DoT) method. It visually explains how DoT works by showing a sequence of latent variables representing thoughts, which diffuse over time in parallel, allowing reasoning steps to occur concurrently. The figure also contrasts DoT with its multi-pass variant (DoTMP), highlighting how DoTMP generates rationales one at a time to address causal bias, making it more suitable for complex reasoning. The use of stacked circles represents the model’s implicit marginalization over other potential reasoning paths during training.
read the caption
Figure 2: Demonstration of DoT pipeline. DoT diffuses all possible thoughts across diffusion timestep t. Multi-pass DoT disentangles each rationale and introduces causal bias. The stacked circles stand for the marginalization over other potential reasoning paths, which is implicitly carried out during the training of diffusion models.
More on tables

🔼 This table presents the main experimental results of different reasoning approaches on three tasks: four-digit multiplication, five-digit multiplication, boolean logic, and grade school math problems. It compares the accuracy and throughput (samples per second) of various models, including different variations of the proposed Diffusion of Thought (DoT) method, against several baselines like autoregressive models with chain-of-thought prompting and implicit chain-of-thought. The results highlight DoT’s ability to achieve high accuracy and efficiency.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.

🔼 This table presents the main results of the experiments conducted on four different problem-solving reasoning tasks: 4x4 multiplication, 5x5 multiplication, boolean logic, and GSM8K (Grade School Math). For each task, it shows the accuracy and throughput of various models, including different sizes of GPT-2 with and without Chain-of-Thought (CoT), Implicit CoT, and the proposed Diffusion-of-Thought (DoT) method using different base diffusion models (from scratch, Plaid, and SEDD). The accuracy metric measures the percentage of correctly predicted answers, while throughput indicates the number of samples processed per second. The table also highlights results using self-consistency decoding.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.

🔼 This table presents the main experimental results, comparing different models’ performance across various reasoning tasks. It shows accuracy and throughput (samples processed per second) for four-digit and five-digit multiplication, boolean logic, and grade-school math problems (GSM8K). The models compared include various GPT-2 sizes with and without Chain-of-Thought (CoT), Implicit CoT, and the proposed Diffusion-of-Thought (DoT) with different base diffusion models (from-scratch, Plaid, and SEDD). Bracketed numbers show results using self-consistency decoding.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.

🔼 This table presents the performance comparison of different models on three reasoning tasks: 4x4 digit multiplication, 5x5 digit multiplication, boolean logic, and grade school math (GSM8K). For each task, it shows the accuracy and throughput of various models including autoregressive models (GPT2 with different sizes, ChatGPT), autoregressive models with chain-of-thought (CoT), implicit CoT, and the proposed Diffusion-of-Thought (DoT) with different base diffusion models (Plaid and SEDD). It highlights the accuracy and throughput of single-pass and multi-pass DoT, comparing them to baseline methods. Bracketed numbers show improvements gained by using self-consistency.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.
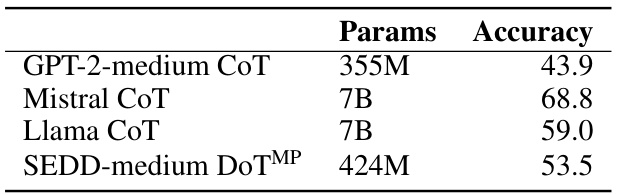
🔼 This table presents the main experimental results comparing different reasoning approaches on three tasks: four-digit and five-digit multiplication, boolean logic, and grade school math problems. It shows the accuracy and throughput (samples per second) for various models, including autoregressive models with Chain-of-Thought (CoT), Implicit CoT, and the proposed Diffusion-of-Thought (DoT) method with different diffusion models. The table highlights DoT’s competitive performance and efficiency, especially when using self-consistency. Bracketed numbers show the improvement in accuracy gained through the use of self-consistency.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.

🔼 This table presents the main experimental results comparing different models’ performance on various reasoning tasks: four-digit and five-digit multiplication, boolean logic, and grade school math problems (GSM8K). The metrics used are accuracy (the percentage of correctly solved problems) and throughput (samples processed per second). The table compares several baselines including different sizes of GPT-2 with and without chain-of-thought (CoT), Implicit CoT, and the proposed Diffusion-of-Thought (DoT) method using different diffusion models (Plaid and SEDD) and training approaches. Bracketed accuracy numbers indicate the performance improvement after applying self-consistency.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.

🔼 This table presents the main experimental results comparing different models on three reasoning tasks: four-digit and five-digit multiplication, boolean logic, and grade school mathematics (GSM8K). It shows the accuracy and throughput (samples per second) for each model. Baselines include autoregressive models (GPT-2) with and without Chain-of-Thought (CoT), Implicit CoT, and ChatGPT. The main focus is on the proposed Diffusion-of-Thought (DoT) method using different base diffusion models (from scratch, Plaid, and SEDD). The table also shows the improvement achievable using self-consistency.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.

🔼 This table presents the main results of the experiments conducted on various reasoning tasks, including multi-digit multiplication, boolean logic, and grade school math problems. It compares the accuracy and throughput (samples per second) of different models, including various diffusion models with the proposed DoT method, autoregressive models with and without chain-of-thought (CoT), and implicit CoT. The results showcase the effectiveness of DoT in improving both accuracy and efficiency, especially in more complex tasks. Bracketed values show the improvement achieved through self-consistency.
read the caption
Table 1: The main results on different problem-solving reasoning tasks. Acc (↑) is to measure the exact match accuracy of the predicted final answer. Throughput (↑) measures the number of samples processed per second during test with batch size equals to 1. The baseline results for Mult. and GSM8K datasets are taken from the implicit CoT paper [7] and have been validated for reproducibility by us. Bracketed numbers indicate the self-consistency results.
Full paper#