Speculative Monte-Carlo Tree Search

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents a novel approach to parallelize Monte Carlo Tree Search (MCTS), a crucial algorithm in AI decision-making. By addressing the sequential nature of MCTS, it significantly reduces training time and opens new avenues for improving the efficiency of AI systems. This is highly relevant to researchers working on AlphaZero-like algorithms and broader applications of MCTS in various fields. The proposed method and analytical model offer valuable insights for future research in efficient AI algorithms.

Visual Insights

#

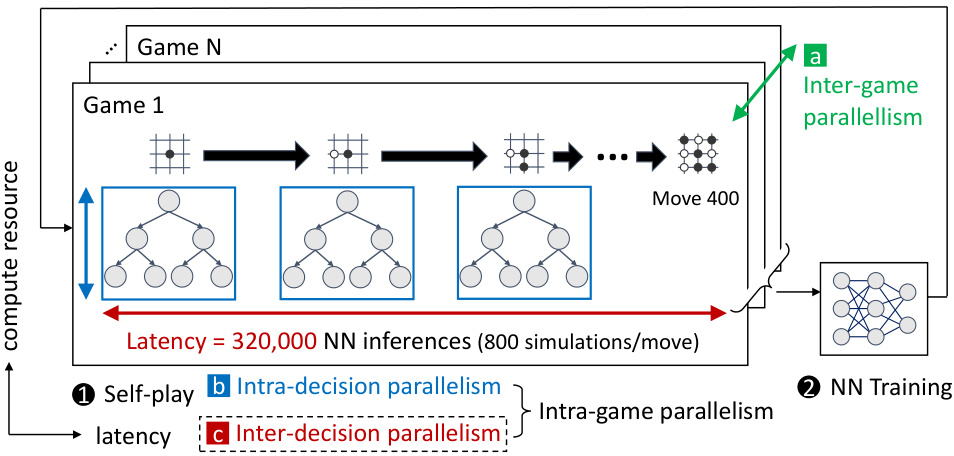
The figure illustrates the AlphaZero training process, which involves self-play and neural network training. The self-play phase is highlighted as being highly resource-intensive. The caption breaks down the parallelism within the self-play phase into three categories: (a) Inter-game parallelism: This is embarrassingly parallel, meaning multiple games can be run concurrently. (b) Intra-decision parallelism: This involves parallel search algorithms within a single move, such as parallel Monte Carlo Tree Search (MCTS). (c) Inter-decision parallelism: This involves the parallel execution of future moves before the current move’s computation is finished, which is the problem the paper aims to address. The figure visually depicts the sequential nature of the MCTS process, indicating a high latency, and shows that the paper’s proposed method will focus on improving inter-decision parallelism.

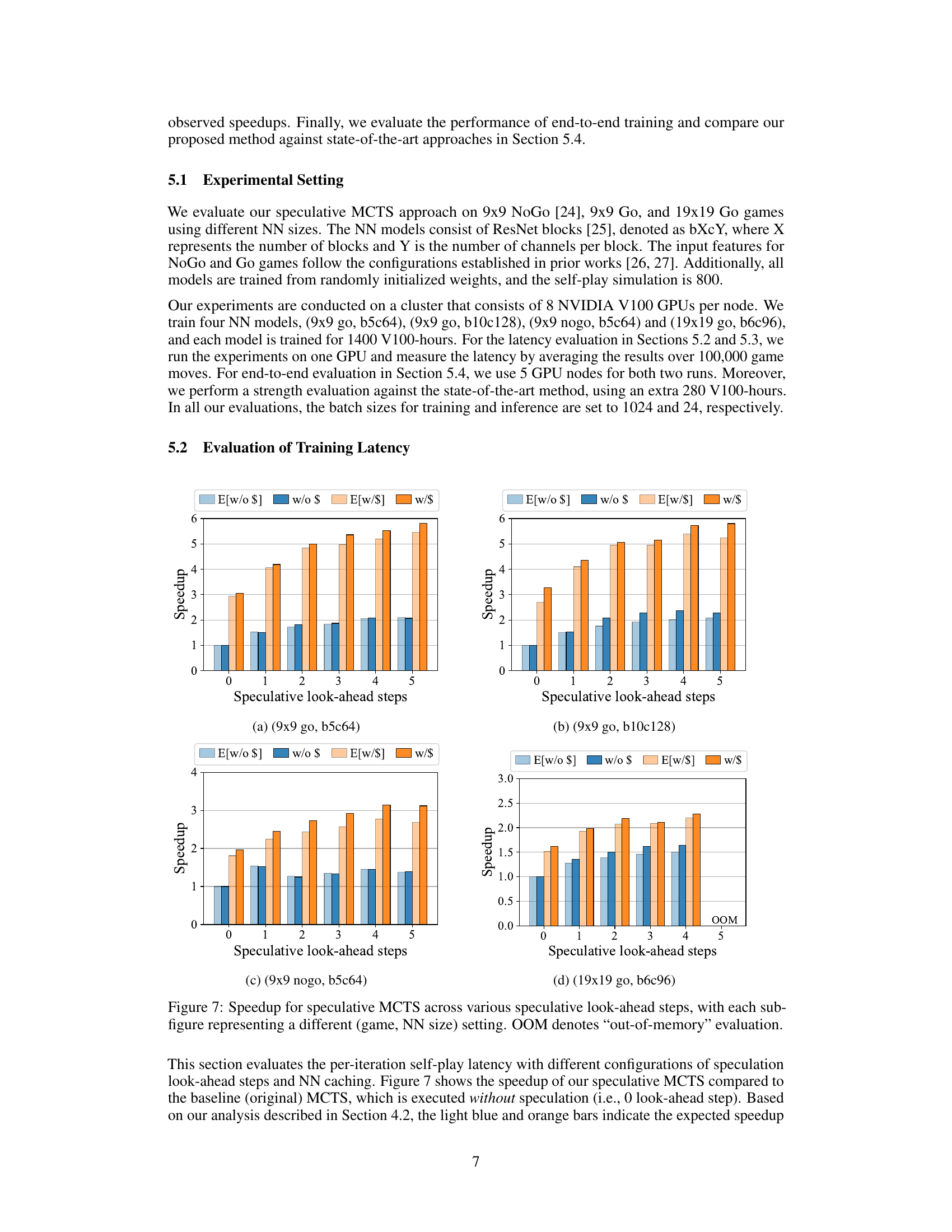
This figure presents the results of evaluating the speedup achieved by the proposed speculative MCTS approach. Different settings are used, varying the number of speculative look-ahead steps and the size of the neural network (NN). Each subfigure shows the results for a specific game (9x9 Go, 9x9 NoGo, or 19x19 Go) and NN configuration. The speedup is calculated relative to the baseline (original) MCTS execution without speculation. The ‘OOM’ label indicates scenarios where the evaluation ran out of memory.

In-depth insights

#

Speculative MCTS

#

Speculative Monte-Carlo Tree Search (MCTS) introduces a novel parallelization strategy to address the inherent sequential nature of traditional MCTS. By leveraging the anytime property of MCTS, future moves are predicted and executed speculatively in parallel with the current move’s computation. This pipeline approach significantly reduces training latency, as demonstrated by a speedup of up to 5.8x in 9x9 Go games. The synergy between speculative execution and neural network caching further enhances performance by boosting cache hit rates. An analytical model provides a valuable framework to estimate the potential speedup for various speculation strategies before deployment. Although promising, the method’s efficiency might be affected by the accuracy of future move predictions, which are based on partial simulation results from the current move. Further investigation into the optimal look-ahead steps and the robustness of prediction under various conditions is necessary to fully realize the potential of speculative MCTS.

Parallelism Synergy

#

The concept of “Parallelism Synergy” in the context of a research paper likely refers to the combined effect of multiple parallel processing strategies exceeding the sum of their individual contributions. This could involve techniques such as inter-game, intra-decision, and inter-decision parallelism, where each method addresses a different aspect of computational latency. The synergistic effect arises from the interaction and optimization between these strategies. For instance, inter-decision parallelism (speculative execution) might benefit from intra-decision parallelism (parallel search algorithms) by reducing the impact of individual move computation time. Furthermore, a technique like neural network caching can enhance all parallel approaches by reducing redundant computations, thus creating a powerful synergy. The overall result is a significant performance improvement exceeding a simple linear speedup, which is a hallmark of effective parallelism synergy.

Analytical Model

#

The ‘Analytical Model’ section in a research paper is crucial for evaluating the effectiveness of a proposed method, especially when dealing with complex systems like speculative Monte Carlo Tree Search (MCTS). A strong analytical model provides a quantitative framework to predict performance gains and resource consumption under different parameter settings (like look-ahead steps). This allows researchers to understand and optimize the trade-offs between speculation and computational cost, potentially identifying the most efficient configuration before time-consuming simulations are run. The accuracy of such a model is essential; it must correctly reflect the underlying process of speculative MCTS, capturing the dynamics of pipeline execution including successes and failures. Ultimately, a robust analytical model provides valuable insights for decision-making and serves as a foundation for future improvements and extensions of the work. Its value lies in its ability to both guide practical deployments and advance theoretical understanding of speculative parallel techniques within the context of MCTS.

Training Speedup

#

The research paper explores methods to significantly enhance the training speed of AlphaZero-like game AI models. A core focus is on addressing the sequential nature of Monte-Carlo Tree Search (MCTS), a critical component. The proposed solution, speculative MCTS, introduces inter-decision parallelism by speculatively executing future moves concurrently with current move computations. This approach, combined with neural network caching, yields substantial speed improvements. Empirical results demonstrate up to a 5.8x speedup in 9x9 Go training and a 1.91x improvement over the state-of-the-art KataGo in 19x19 Go training. An analytical model provides insight into potential speed gains before full implementation. The synergy between speculation and caching is particularly impactful, showcasing the potential of combining different parallelization strategies. Further research could explore optimizing speculation strategies and expanding the methodology to other applications requiring sequential decision making.

Future Directions

#

Future research could explore adaptive speculation strategies, dynamically adjusting the lookahead based on the game’s phase and MCTS progress. Investigating alternative prediction models beyond simple move prediction, such as predicting entire sequences of moves or game outcomes, could significantly enhance efficiency. Integrating speculative MCTS with other parallel MCTS algorithms presents opportunities for synergistic speedups, leveraging both intra- and inter-decision parallelism. A key area for improvement lies in developing more robust speculation mechanisms to minimize the overhead associated with mispredictions. Finally, evaluating the scalability of speculative MCTS on larger games and more complex AI tasks is essential for establishing its broad applicability and demonstrating its practical value for high-stakes decision-making scenarios.

More visual insights

#

More on figures

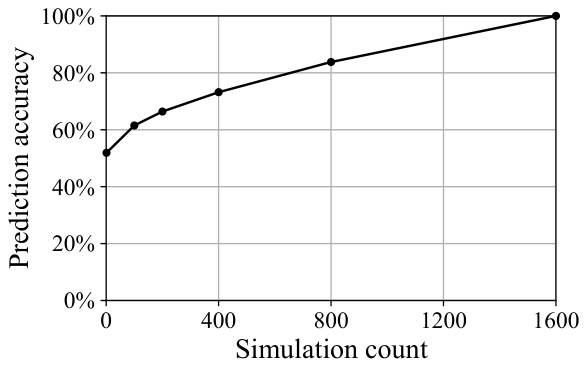
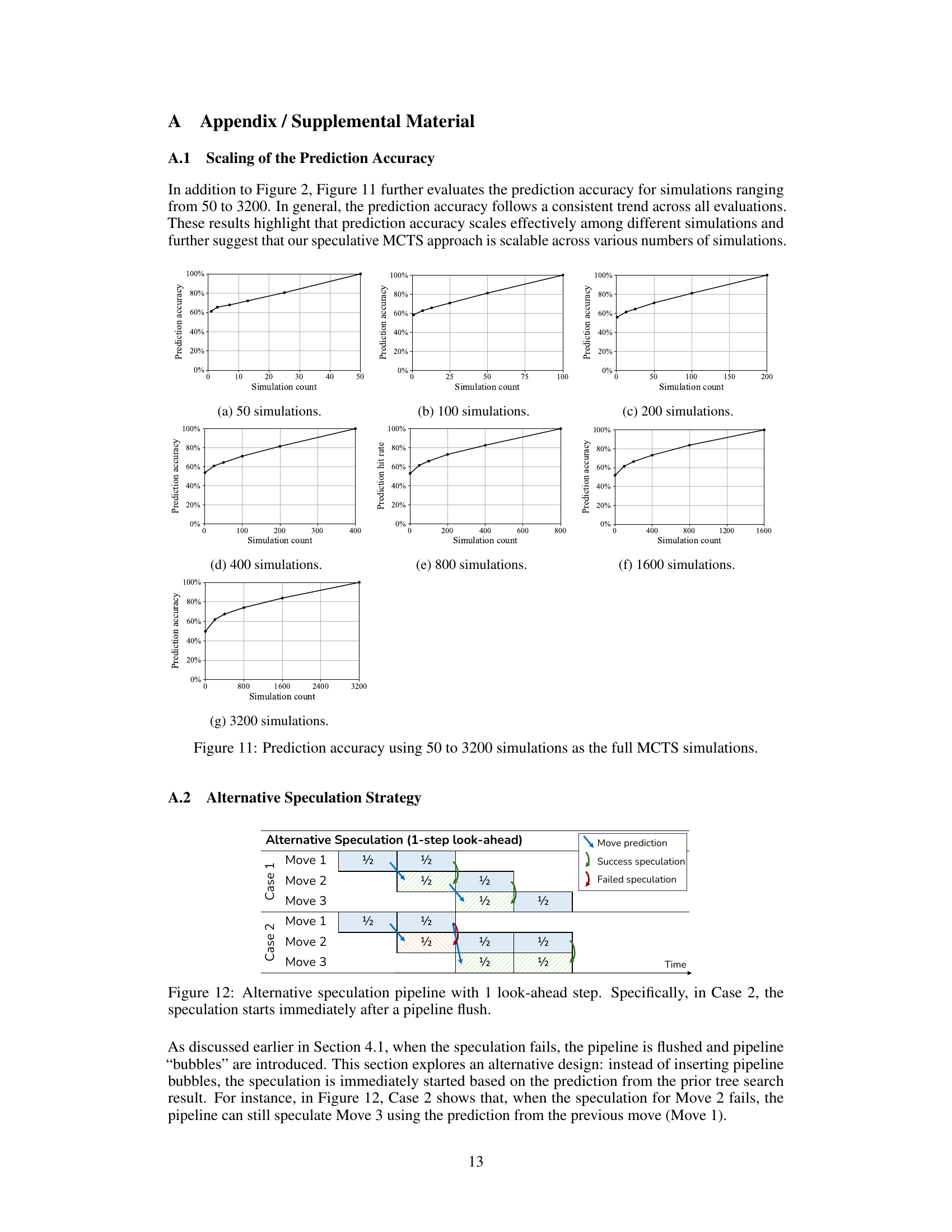
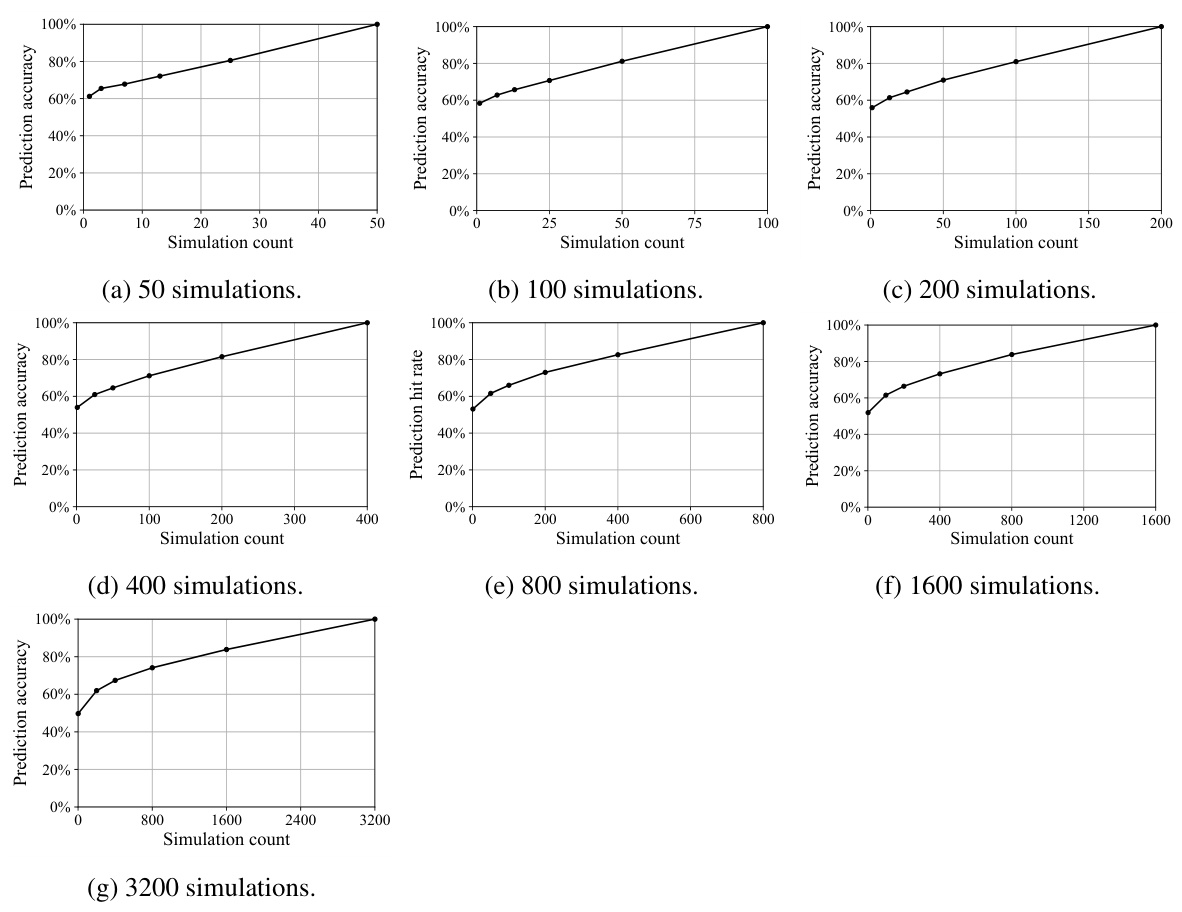
The figure shows the prediction accuracy when using a smaller number of simulations to predict the results of a full MCTS search with 1600 simulations. The x-axis represents the number of simulations used for prediction, and the y-axis represents the prediction accuracy. The graph shows that as the number of simulations used for prediction increases, the prediction accuracy also increases, demonstrating that partial MCTS searches can reasonably predict the full MCTS results.

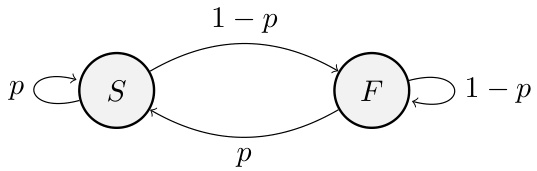
This figure is a finite state machine representing the speculation pipeline in Figure 3(b). It has two states: a successful (S) state and a failed (F) state. The probability of a successful prediction is represented by p. The transitions between states are determined by the prediction accuracy.

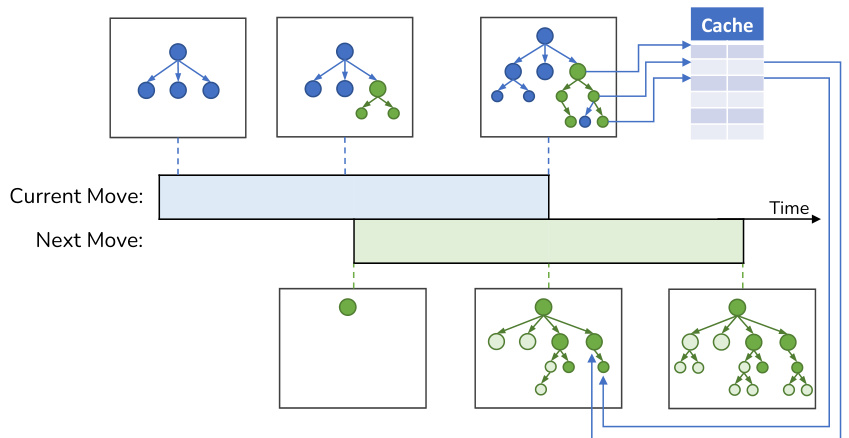
This figure illustrates how speculative MCTS improves efficiency by sharing cached neural network (NN) inference results between parallel moves. The diagram shows that while the current move’s MCTS simulation is in progress, the next move’s simulation begins speculatively, using the cached results from the current move. This overlap reduces latency, even if the speculative prediction for the next move is incorrect, because cached results from discarded nodes can still be utilized for the current move. The cache is represented as a table storing NN inference results, allowing for faster retrieval when the same node is encountered in subsequent moves.

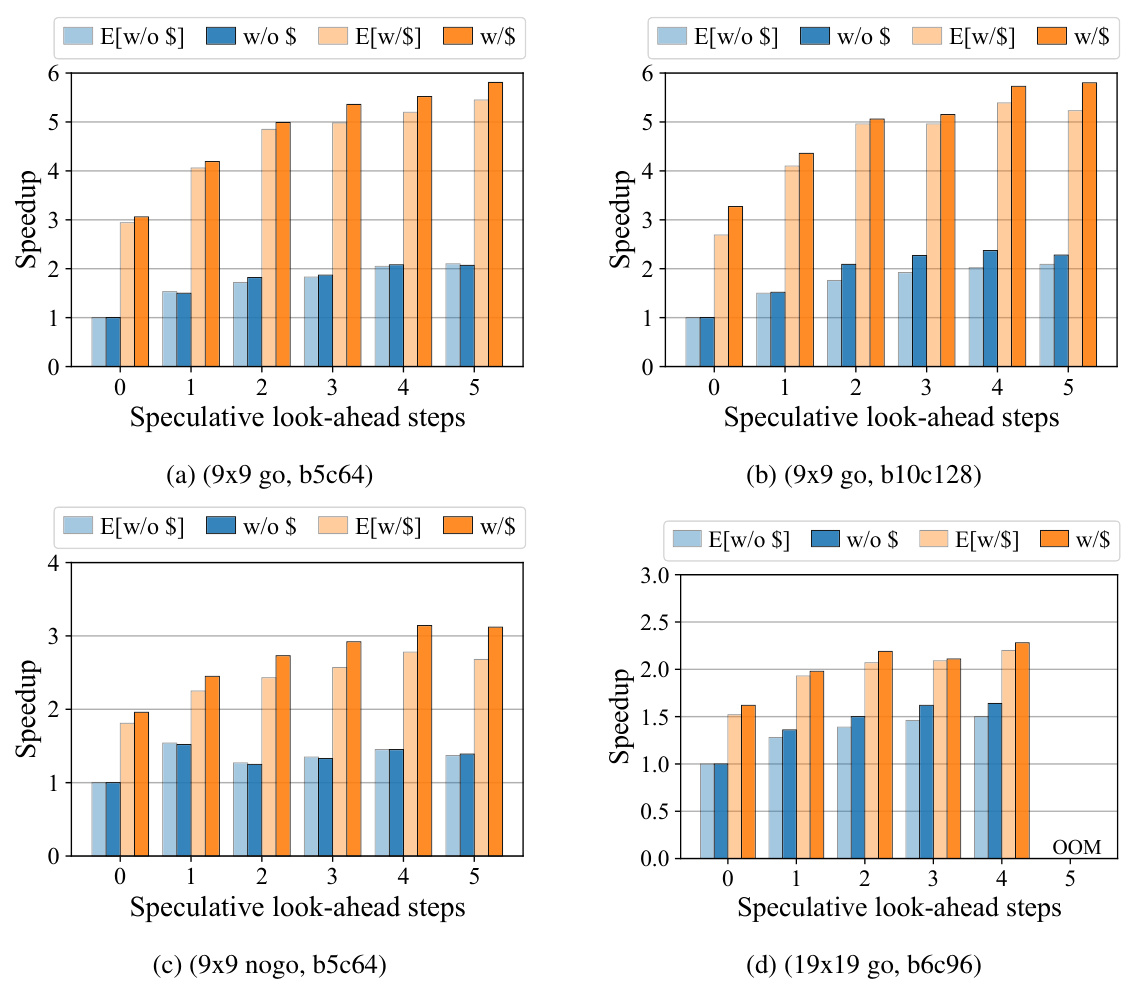
This figure presents the results of evaluating the per-iteration self-play latency with different speculation look-ahead steps and NN caching. Each sub-figure represents a different combination of game and neural network (NN) size. The x-axis shows the number of speculative look-ahead steps, while the y-axis shows the speedup achieved compared to the baseline (original) MCTS with no speculation (0 look-ahead steps). The bars represent the speedup, broken down into estimated values (light blue and orange) and evaluated values (dark blue and orange), with and without NN caching. OOM indicates that the evaluation ran out of memory.

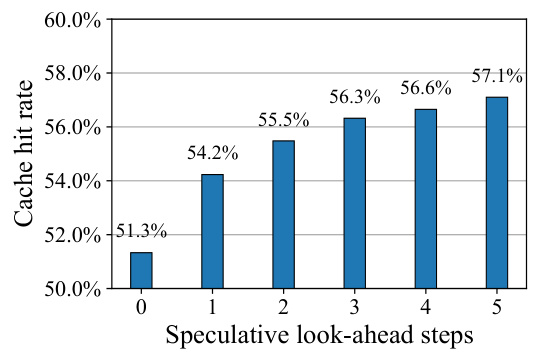
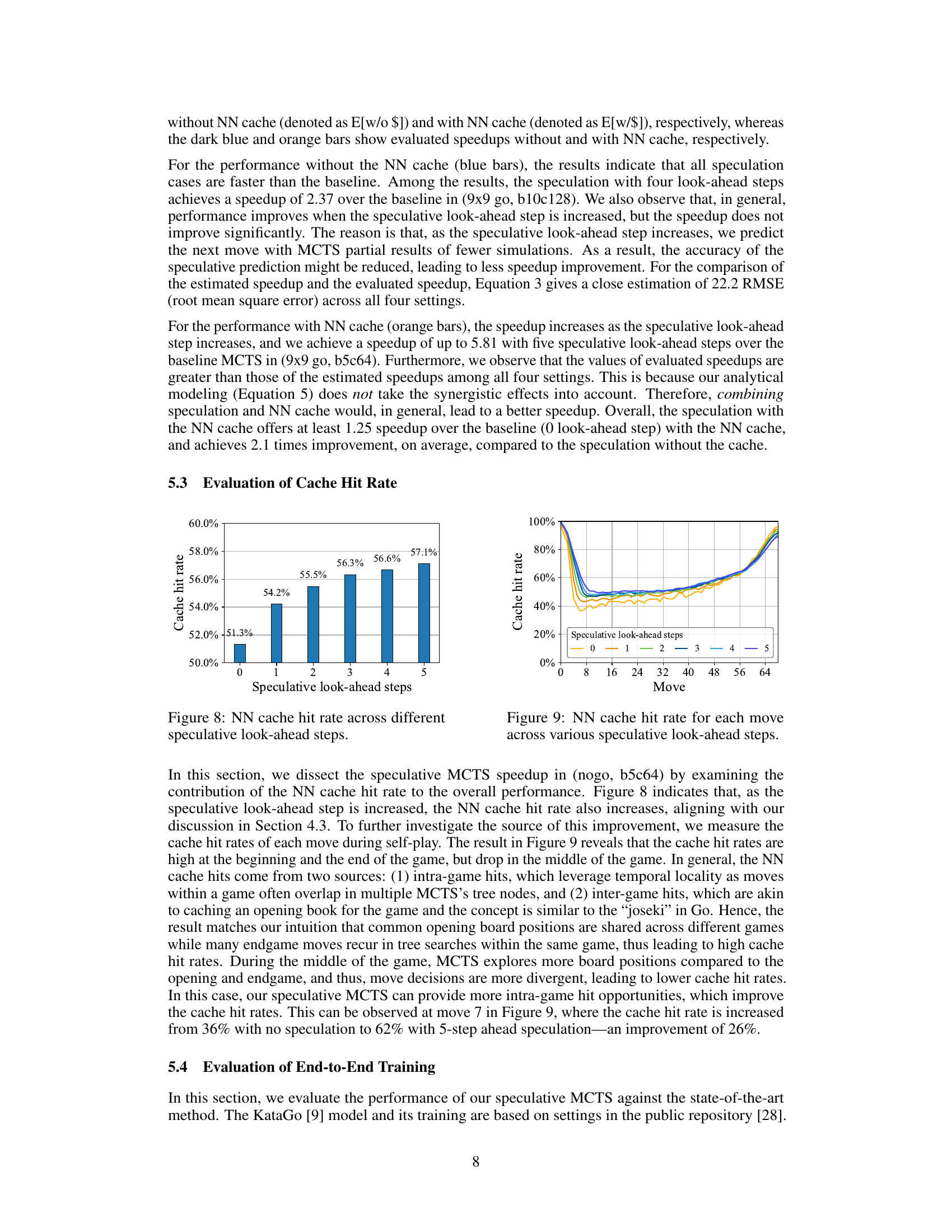
This figure shows the Neural Network (NN) cache hit rate for different numbers of speculative look-ahead steps in speculative Monte Carlo Tree Search (MCTS). The x-axis represents the number of speculative look-ahead steps, and the y-axis represents the cache hit rate. As the number of speculative look-ahead steps increases, the NN cache hit rate also increases. This demonstrates the synergy between speculation and NN caching in improving performance.

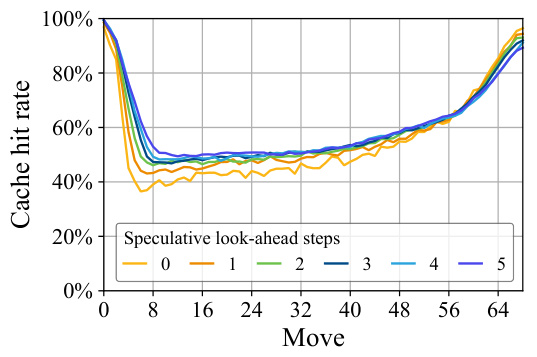
This figure displays the NN cache hit rate for each move during the game, categorized by the number of speculative look-ahead steps used in the speculative MCTS algorithm. It illustrates how the cache hit rate changes throughout a game (x-axis representing moves), varying with different speculation strategies (different lines representing different look-ahead steps). This helps visualize the impact of speculation on cache utilization. Generally, higher speculation leads to a higher cache hit rate, particularly in the beginning and end game where similar game states are more likely to occur.

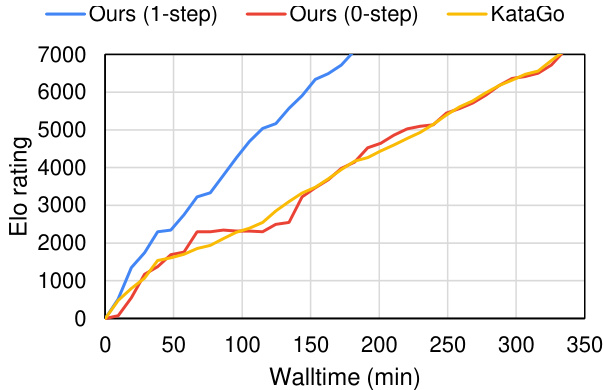
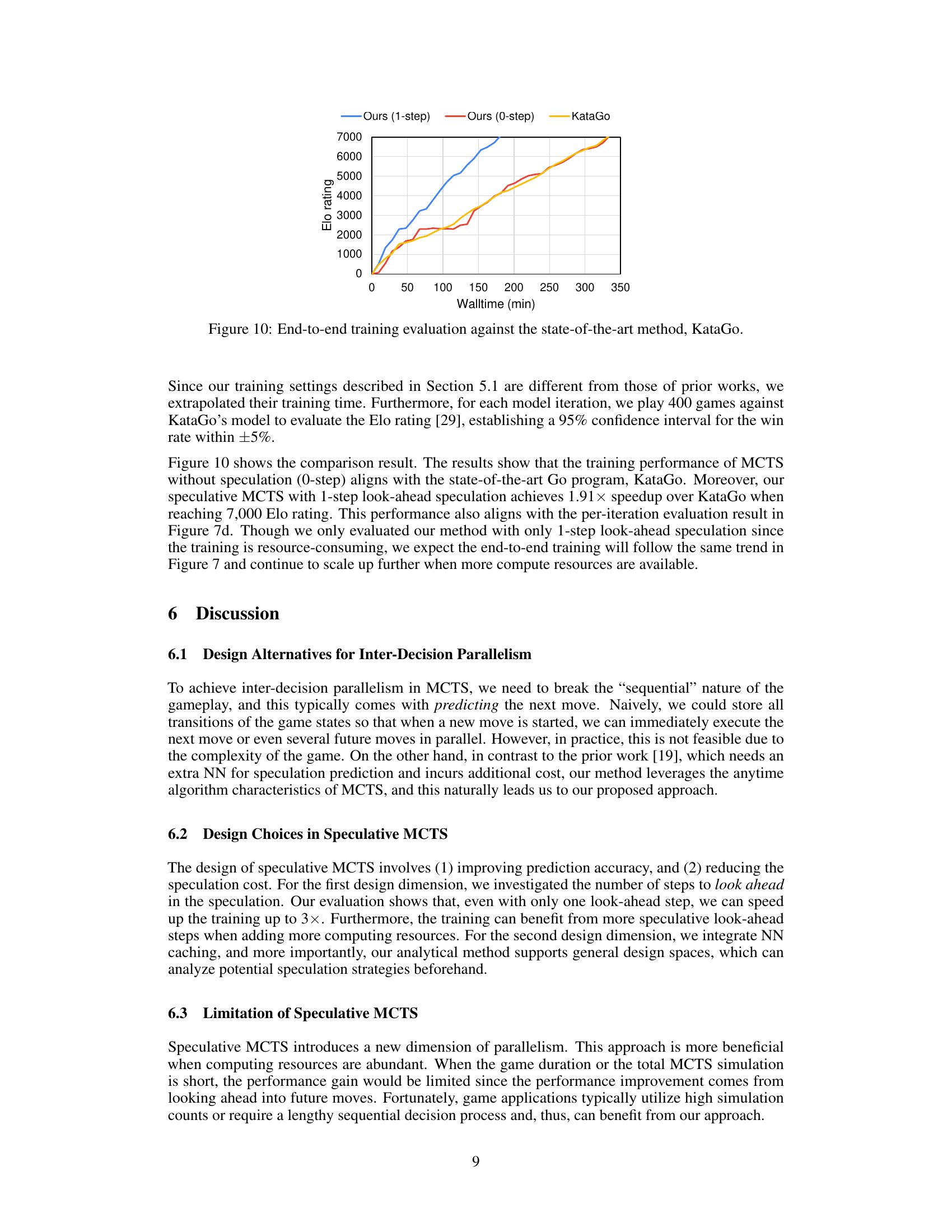
This figure shows the comparison of end-to-end training performance between the proposed speculative MCTS method and the state-of-the-art KataGo program. The x-axis represents the wall-clock time in minutes, and the y-axis represents the Elo rating, a measure of performance. Three lines are presented: one for the proposed speculative MCTS with 1-step look-ahead, one for the proposed speculative MCTS without speculation (0-step look-ahead), and one for KataGo. The figure shows that the speculative MCTS with 1-step look-ahead achieves a significant speedup compared to KataGo while reaching the same Elo rating.

This figure evaluates the per-iteration self-play latency with different configurations of speculation look-ahead steps and NN caching. The speedup of the speculative MCTS, compared to the baseline (original) MCTS, is shown for various game and neural network sizes. The light blue and orange bars represent the expected speedup (without and with NN caching respectively), and the dark blue and orange bars show the actual speedup (without and with NN caching respectively).

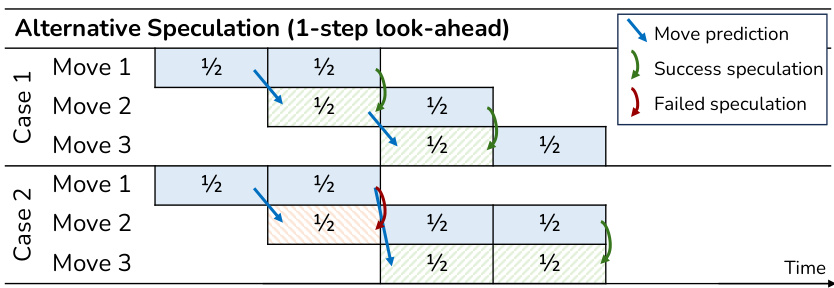
This figure illustrates the difference between the original sequential MCTS execution and the proposed speculative MCTS. In the original method (a), each move is processed sequentially, completing one half of the MCTS computation before moving on. In the speculative method (b), the next move’s computation starts based on the prediction from the current move. The figure shows how this speculative execution is pipelined and the possibility of successful or failed speculations, influencing the overall computation time.

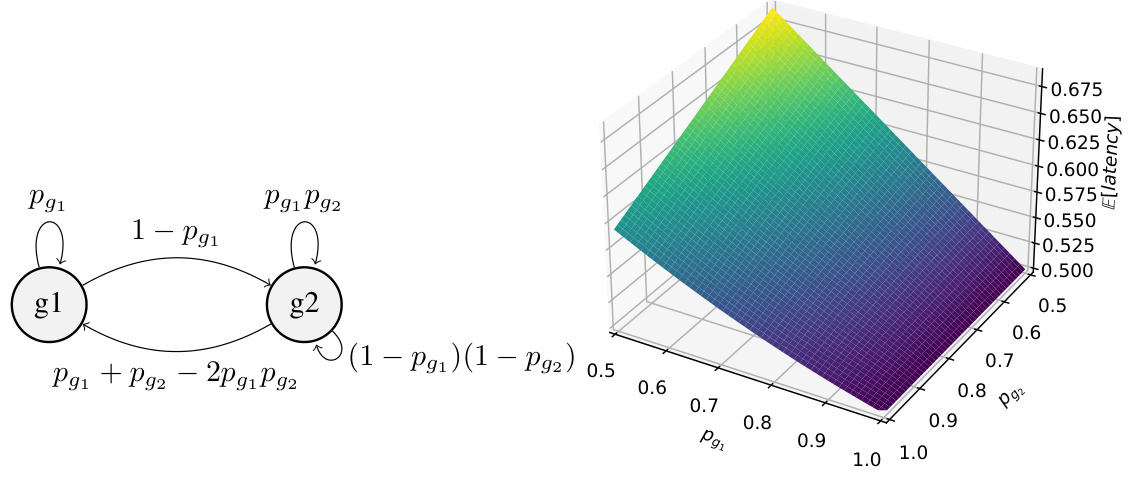
This figure depicts a finite state machine that models a speculation pipeline with two stages. The states represent successful (g1) and failed (g2) speculation attempts for predicting the next move in a game. The transition probabilities between the states are based on the prediction accuracy (Pg1 and Pg2) for each stage, showing the probability of transitioning to a successful or failed prediction depending on the results of the current step.

Full paper

#