TL;DR#
Traditional Temporal Domain Generalization (TDG) methods struggle with real-world scenarios where data is collected at irregular intervals and evolves continuously. This paper introduces Continuous Temporal Domain Generalization (CTDG) to address this limitation. Existing TDG approaches often fail to capture the continuous evolution of data and model dynamics.
The proposed Koopman operator-driven continuous temporal domain generalization (Koodos) framework tackles CTDG by modeling continuous data dynamics and model evolution using Koopman theory. Koodos also incorporates optimization strategies and inductive bias. Extensive experiments showed Koodos’s effectiveness and efficiency in handling CTDG problems, significantly outperforming existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the limitations of existing temporal domain generalization (TDG) methods, which primarily focus on discrete-time data. By introducing the concept of continuous TDG (CTDG) and proposing the Koopman operator-driven framework (Koodos), this research opens new avenues for modeling and generalizing models in dynamic environments with irregularly observed and continuous-time data. This is highly relevant to various fields dealing with continuous temporal data, such as healthcare, finance, and environmental science, and will likely spur further research in CTDG and continuous-time dynamical systems.
Visual Insights#

🔼 This figure illustrates the concept of Continuous Temporal Domain Generalization (CTDG) using the example of public opinion prediction from tweets. Training data is only available during specific political events, resulting in irregularly spaced data points across continuous time. The goal is to train a model that generalizes to future time points and accurately predicts public opinion even with data distribution shifts.
read the caption
Figure 1: An example of continuous temporal domain generalization. Consider training classification models for public opinion prediction via tweets, where the training domains are only available at specific political events (e.g., presidential debates), we wish to generalize the model to any future based on the underlying data distribution drift within the time-irregularly distributed training domains.

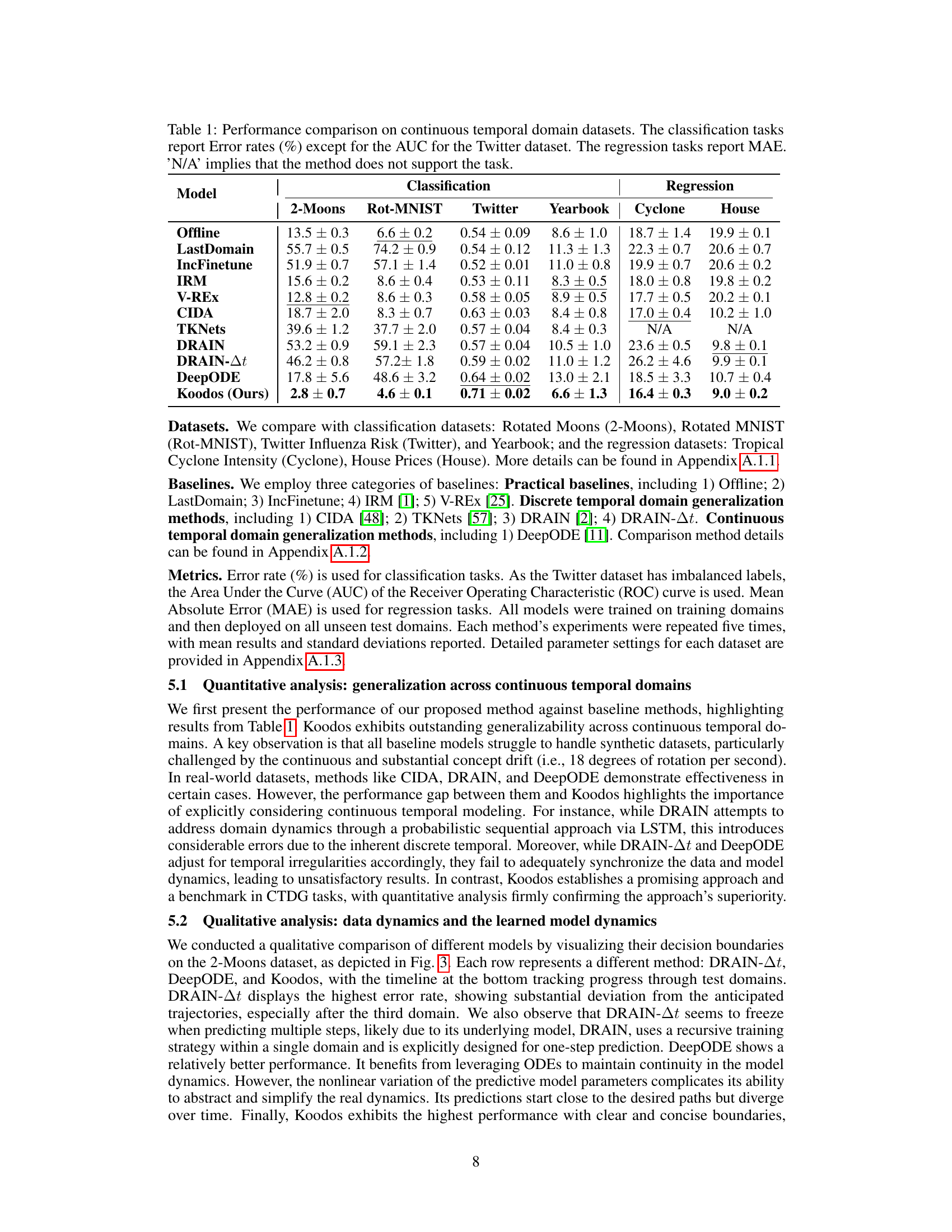
🔼 This table presents a comparison of different models’ performance on several continuous temporal domain datasets. The datasets include both classification and regression tasks, using various metrics to evaluate performance. Error rates (percentage) are reported for classification, except for the Twitter dataset where AUC is used. Mean Absolute Error (MAE) is used for the regression tasks. The table highlights Koodos’ performance against several baselines, indicating its effectiveness across various datasets.
read the caption
Table 1: Performance comparison on continuous temporal domain datasets. The classification tasks report Error rates (%) except for the AUC for the Twitter dataset. The regression tasks report MAE. 'N/A' implies that the method does not support the task.
In-depth insights#
Koopman CTDG#
Koopman operator theory provides a powerful framework for analyzing and modeling dynamical systems, particularly those with high dimensionality or nonlinearity. Applying this to Continuous Temporal Domain Generalization (CTDG) offers a unique approach. The core idea is to leverage the Koopman operator to represent the continuous evolution of both the data and the predictive model’s parameters in a lower-dimensional, linearized space. This linearization significantly simplifies the complex dynamics inherent in CTDG. By formulating the problem within a continuous dynamical system, the Koopman-based approach allows for accurate characterization of continuous data drifts. The optimization process involves jointly learning the predictive model, the Koopman operator, and the associated transformation functions, ensuring a coherent representation across different spaces. This framework effectively captures the continuous dynamics, enabling robust generalization to unseen continuous temporal domains and addressing challenges related to high dimensionality and nonlinearity. The introduction of inductive biases based on prior knowledge further refines and enhances the generalization performance. In essence, Koopman CTDG presents an innovative and efficient method for handling the complexities of continuous-time data and model dynamics in a principled manner.
Model Dynamics#
The concept of ‘Model Dynamics’ in a machine learning context refers to how a model’s internal state changes over time. This is particularly relevant when dealing with time-series data or situations where the underlying data distribution evolves. Understanding model dynamics is crucial for assessing a model’s robustness, generalization ability, and its capacity to adapt to changing environments. Analyzing these dynamics allows for the identification of potential issues like overfitting or instability. For instance, if a model’s parameters exhibit chaotic behavior over time, it may indicate poor generalization capability. Conversely, a stable, predictable pattern may show the ability of a model to capture underlying temporal regularities. Techniques to study model dynamics often involve analyzing the evolution of model parameters, latent variables, or even the model’s output distribution over time. Methods such as visualizing parameter trajectories, assessing model stability via eigenvalues, or using Koopman operator theory are crucial for characterizing these dynamics. The practical implications are significant, as these insights help to improve model design, training strategies, and ultimately, the performance and reliability of machine learning systems. Incorporating knowledge about desired model dynamics can also lead to better generalization, for example, by imposing constraints on the model’s trajectory to reflect prior knowledge of the system’s behavior.
Nonlinearity#
The concept of nonlinearity is crucial in many scientific fields, including the study of complex systems and dynamic processes. Nonlinear systems exhibit behaviors that are not proportional to their inputs, unlike linear systems. This disproportionality can lead to a wide range of unexpected and often chaotic outcomes. A key characteristic of nonlinearity is the presence of feedback loops, where the output of a system influences its subsequent input. This can create a self-reinforcing effect, leading to either rapid growth or sudden collapse, depending on the nature of the feedback. Understanding nonlinearity requires going beyond simple cause-and-effect relationships, as multiple factors often interact in complex and unpredictable ways. Analyzing nonlinear systems often relies on sophisticated mathematical tools and computational methods, as they defy the simple linear models that can often be used to describe simpler systems. The challenges posed by nonlinearity highlight the limitations of linear thinking, emphasizing the need for more robust and adaptable models capable of handling complex interactions and unforeseen consequences. Furthermore, the inherent unpredictability of nonlinear systems often necessitates a shift from deterministic towards probabilistic approaches, emphasizing uncertainty and potential for multiple outcomes.
Inductive Bias#
Inductive bias, in the context of machine learning, refers to the assumptions baked into a model’s architecture or learning algorithm that guide its generalization. In temporal domain generalization (TDG), inductive bias plays a crucial role in navigating the challenges of continuously evolving data distributions. Without carefully considered biases, models risk overfitting to specific temporal patterns or failing to capture the underlying dynamics. Koopman operator-driven methods offer a structured approach to incorporating inductive bias, allowing for the integration of prior knowledge about the system’s dynamics (e.g., periodicity, convergence) into the learning process. This structured approach contrasts with methods that rely solely on data-driven learning, thereby enhancing model robustness and generalization performance. The choice of inductive bias in TDG should consider the specific characteristics of the temporal data, balancing the need for flexibility with the constraint of preventing overfitting. Effective bias selection enables models to learn more concise and generalizable representations of the underlying dynamics, leading to enhanced predictive capabilities.
Generalization#
The concept of generalization is central to the research paper, focusing on the ability of machine learning models to perform well on unseen data, especially within temporally evolving domains. Continuous Temporal Domain Generalization (CTDG) is introduced as a more challenging and realistic problem setting than traditional TDG, because it involves continuous data streams with irregular temporal intervals. The paper proposes a novel framework, Koodos, designed to tackle the inherent difficulties in characterizing and modeling continuous dynamics in CTDG. Key aspects of the proposed approach include characterizing continuous data and model dynamics, leveraging Koopman operator theory to linearize complex nonlinear dynamics for better generalization, and incorporating prior knowledge about the dynamics through a comprehensive optimization strategy. The effectiveness of Koodos is demonstrated through extensive experiments on diverse datasets, showing improved generalization performance compared to state-of-the-art approaches. Limitations, such as the reliance on certain assumptions about data dynamics and the computational cost associated with continuous-time modeling, are also discussed.
More visual insights#
More on figures

🔼 This figure illustrates the three dynamic flows within the Koodos framework: Data Flow, Model Flow, and Koopman Representation Flow. The Data Flow shows how data changes continuously over time. The Model Flow demonstrates how model parameters change accordingly in response to these data dynamics. The Koopman Representation Flow maps the high-dimensional, nonlinear model dynamics into a low-dimensional, linearized space using the Koopman operator for easier analysis and control. The figure also highlights the micro-constraints (losses) that ensure consistency between the three flows and incorporate prior knowledge.
read the caption
Figure 2: Macro-flows and micro-constraints in the proposed model framework.

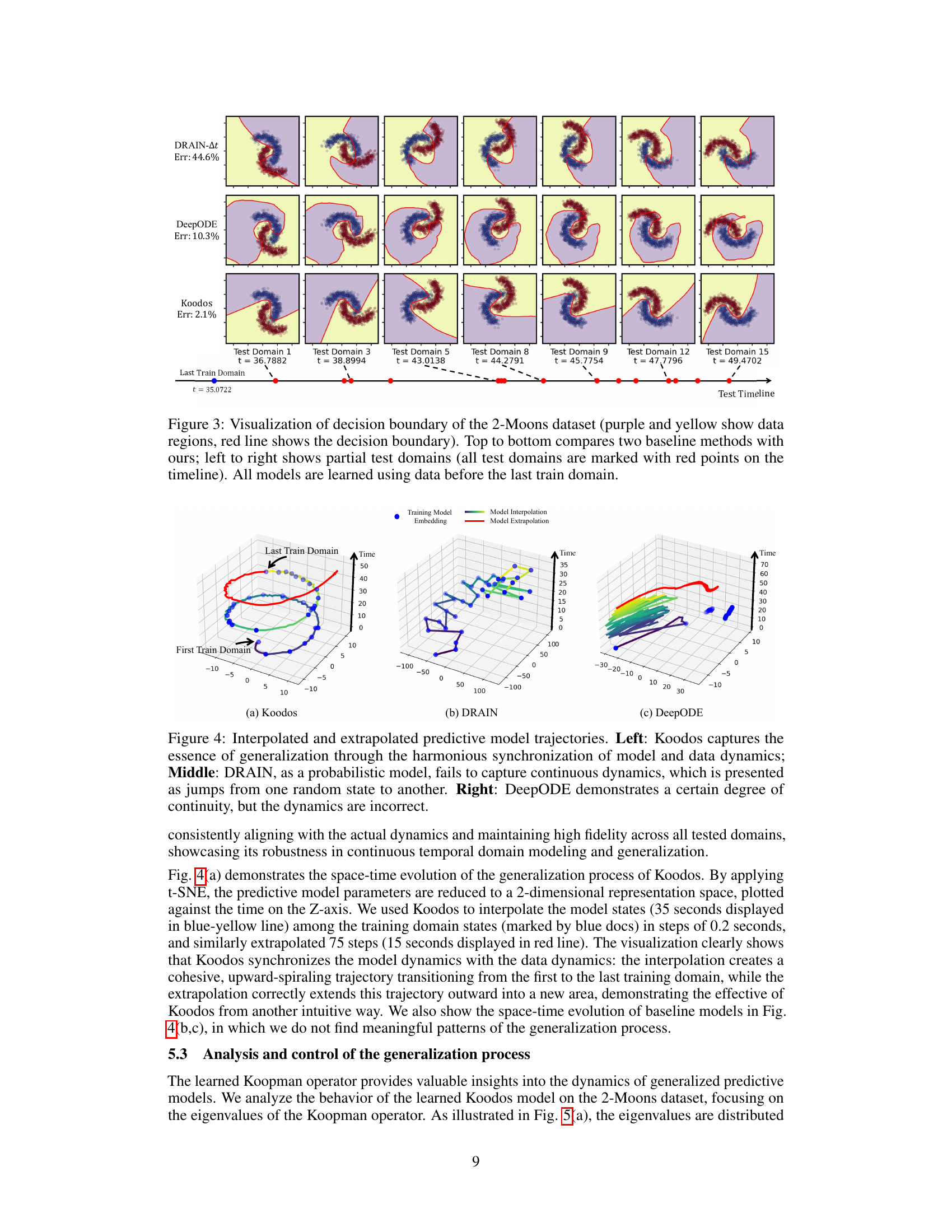
🔼 This figure compares the decision boundaries learned by three different models (DRAIN-Δt, DeepODE, and Koodos) on the 2-Moons dataset across multiple test domains. Each row represents a different model, showcasing its performance in generalizing to unseen domains over time. The red line depicts the learned decision boundary for each domain, while the purple and yellow points show the data points in each domain. The figure visually demonstrates the superior generalization capability of the proposed Koodos model compared to the baselines, especially in maintaining consistent and accurate decision boundaries in unseen domains.
read the caption
Figure 3: Visualization of decision boundary of the 2-Moons dataset (purple and yellow show data regions, red line shows the decision boundary). Top to bottom compares two baseline methods with ours; left to right shows partial test domains (all test domains are marked with red points on the timeline). All models are learned using data before the last train domain.

🔼 This figure compares the performance of Koodos, DRAIN, and DeepODE in terms of model trajectory prediction. Koodos shows smooth and accurate interpolation and extrapolation of model trajectories, aligning well with the data dynamics. DRAIN exhibits discontinuous jumps, failing to capture the continuous nature of the data dynamics. DeepODE shows some degree of continuity but inaccuracies in the predicted dynamics.
read the caption
Figure 4: Interpolated and extrapolated predictive model trajectories. Left: Koodos captures the essence of generalization through the harmonious synchronization of model and data dynamics; Middle: DRAIN, as a probabilistic model, fails to capture continuous dynamics, which is presented as jumps from one random state to another. Right: DeepODE demonstrates a certain degree of continuity, but the dynamics are incorrect.
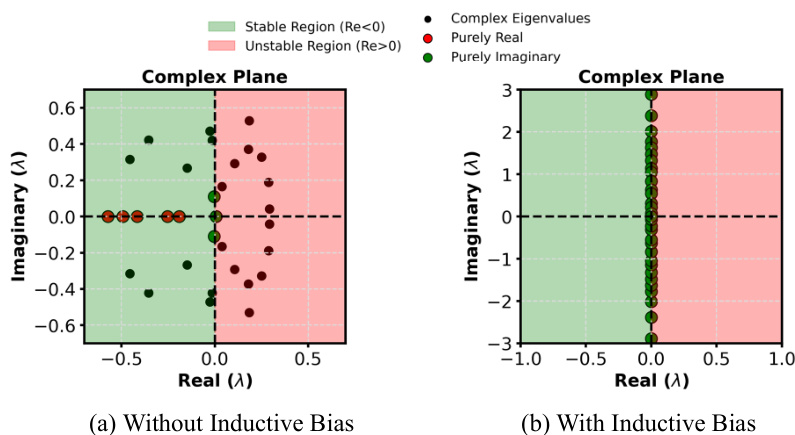
🔼 This figure visualizes the eigenvalue distribution of the Koopman operator, a key component in the Koodos framework. The left panel shows the distribution when the Koopman operator K is learned directly as a parameter of the model. The right panel demonstrates the distribution when K is constrained to be of the form B - Bᵀ, where B is a learnable matrix. This constraint introduces an inductive bias, forcing the eigenvalues to be purely imaginary, promoting stability and periodic behavior in the system’s dynamics. The different distributions illustrate the impact of this inductive bias on the model’s stability and predictive performance.
read the caption
Figure 5: Eigenvalue distribution of the Koopman operator. Left: K as learnable; Right: K = B-BT with B as learnable.
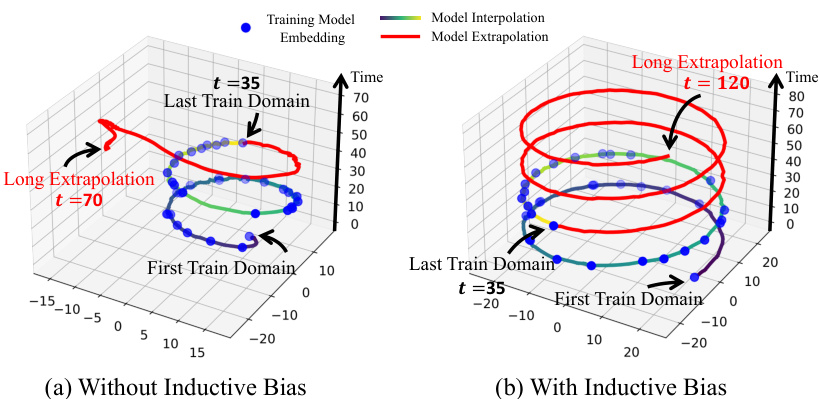
🔼 This figure compares the model trajectories of Koodos, DRAIN, and DeepODE on a continuous temporal domain generalization task. It visualizes how well each model captures and extrapolates the underlying data dynamics. Koodos shows smooth and accurate trajectories that align with the true data dynamics, while DRAIN and DeepODE exhibit limitations in capturing continuous changes.
read the caption
Figure 4: Interpolated and extrapolated predictive model trajectories. Left: Koodos captures the essence of generalization through the harmonious synchronization of model and data dynamics; Middle: DRAIN, as a probabilistic model, fails to capture continuous dynamics, which is presented as jumps from one random state to another. Right: DeepODE demonstrates a certain degree of continuity, but the dynamics are incorrect.

🔼 This figure illustrates the three dynamic flows in the proposed Koodos framework: Data Flow, Model Flow, and Koopman Representation Flow. It shows how the model parameters evolve continuously over time, aligning with the evolving data distributions. The Koopman operator is used to transform the high-dimensional model parameters into a low-dimensional Koopman space where the dynamics are simpler to model. The figure also highlights the use of constraints to ensure consistency between the different flows and to incorporate prior knowledge about the dynamics.
read the caption
Figure 2: Macro-flows and micro-constraints in the proposed model framework.

🔼 This figure illustrates the three dynamic flows in the proposed Koodos framework: Data Flow, Model Flow, and Koopman Representation Flow. It shows how the model’s parameters evolve continuously over time, guided by the data dynamics. The Koopman operator is used to simplify the high-dimensional model dynamics into a low-dimensional space for better understanding and optimization. The figure also highlights the micro-constraints used to ensure consistency between the different representations and flows. It visualizes the interaction between the data space, model space, and Koopman space, emphasizing how the framework synchronizes data and model dynamics for robust continuous temporal domain generalization.
read the caption
Figure 2: Macro-flows and micro-constraints in the proposed model framework.
🔼 This figure compares the decision boundaries learned by three different models (DRAIN-Δt, DeepODE, and Koodos) on the 2-Moons dataset across multiple test domains. The visualization shows how well each model generalizes to unseen domains and their decision boundaries’ evolution over time. It highlights Koodos’s superior performance in maintaining consistent and accurate boundaries even as the data distribution shifts across continuous time.
read the caption
Figure 3: Visualization of decision boundary of the 2-Moons dataset (purple and yellow show data regions, red line shows the decision boundary). Top to bottom compares two baseline methods with ours; left to right shows partial test domains (all test domains are marked with red points on the timeline). All models are learned using data before the last train domain.
More on tables

🔼 This table compares the performance of the proposed Koodos model against various baseline methods on several continuous temporal domain datasets. The datasets are categorized into classification and regression tasks, and performance is measured using error rate (or AUC for Twitter) and Mean Absolute Error (MAE), respectively. The table highlights Koodos’s superior generalization performance across different dataset types.
read the caption
Table 1: Performance comparison on continuous temporal domain datasets. The classification tasks report Error rates (%) except for the AUC for the Twitter dataset. The regression tasks report MAE. 'N/A' implies that the method does not support the task.
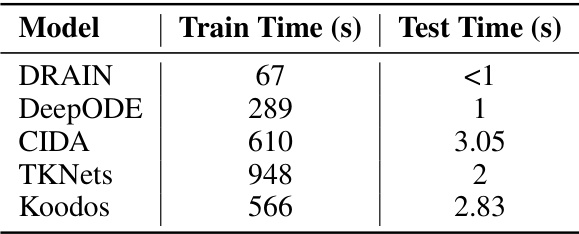
🔼 This table compares the performance of Koodos with other baseline methods across various continuous temporal domain datasets for both classification and regression tasks. The results are presented as error rates (percentage) for classification and Mean Absolute Error (MAE) for regression. It highlights Koodos’s superior performance compared to existing approaches, especially when handling continuous concept drift and irregularly observed temporal domains.
read the caption
Table 1: Performance comparison on continuous temporal domain datasets. The classification tasks report Error rates (%) except for the AUC for the Twitter dataset. The regression tasks report MAE. 'N/A' implies that the method does not support the task.

🔼 This table presents a quantitative comparison of the proposed Koodos method against various baseline methods across several continuous temporal domain datasets. Performance is evaluated using error rates (for classification tasks, except AUC for Twitter) and Mean Absolute Error (MAE, for regression tasks). The table highlights Koodos’s superior generalization ability across different tasks and datasets compared to existing approaches. ‘N/A’ indicates when a specific method does not support the task in question.
read the caption
Table 1: Performance comparison on continuous temporal domain datasets. The classification tasks report Error rates (%) except for the AUC for the Twitter dataset. The regression tasks report MAE. 'N/A' implies that the method does not support the task.
Full paper#