↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Decentralized bilevel optimization, involving multiple agents solving nested optimization problems, is challenging due to data heterogeneity and the need for efficient hyper-gradient estimation. Existing methods often rely on gradient tracking, neglecting other techniques, and use identical strategies for upper and lower levels. These limitations lead to slow convergence and suboptimal performance.
SPARKLE, a novel framework, addresses these issues by offering flexibility in choosing heterogeneity-correction strategies (e.g., EXTRA, Exact Diffusion) and update strategies for different optimization levels. It presents a unified convergence analysis, proving state-of-the-art convergence rates. Experiments demonstrate SPARKLE’s superior performance over existing methods, particularly with EXTRA and Exact Diffusion, highlighting the benefits of mixed strategies.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in decentralized machine learning and bilevel optimization. It offers a unified framework, applicable to various heterogeneity-correction techniques and mixed update strategies, thus advancing the state-of-the-art in decentralized bilevel optimization. The unified convergence analysis and experimental results provide valuable insights for algorithm design and future research, addressing limitations of existing methods.
Visual Insights#

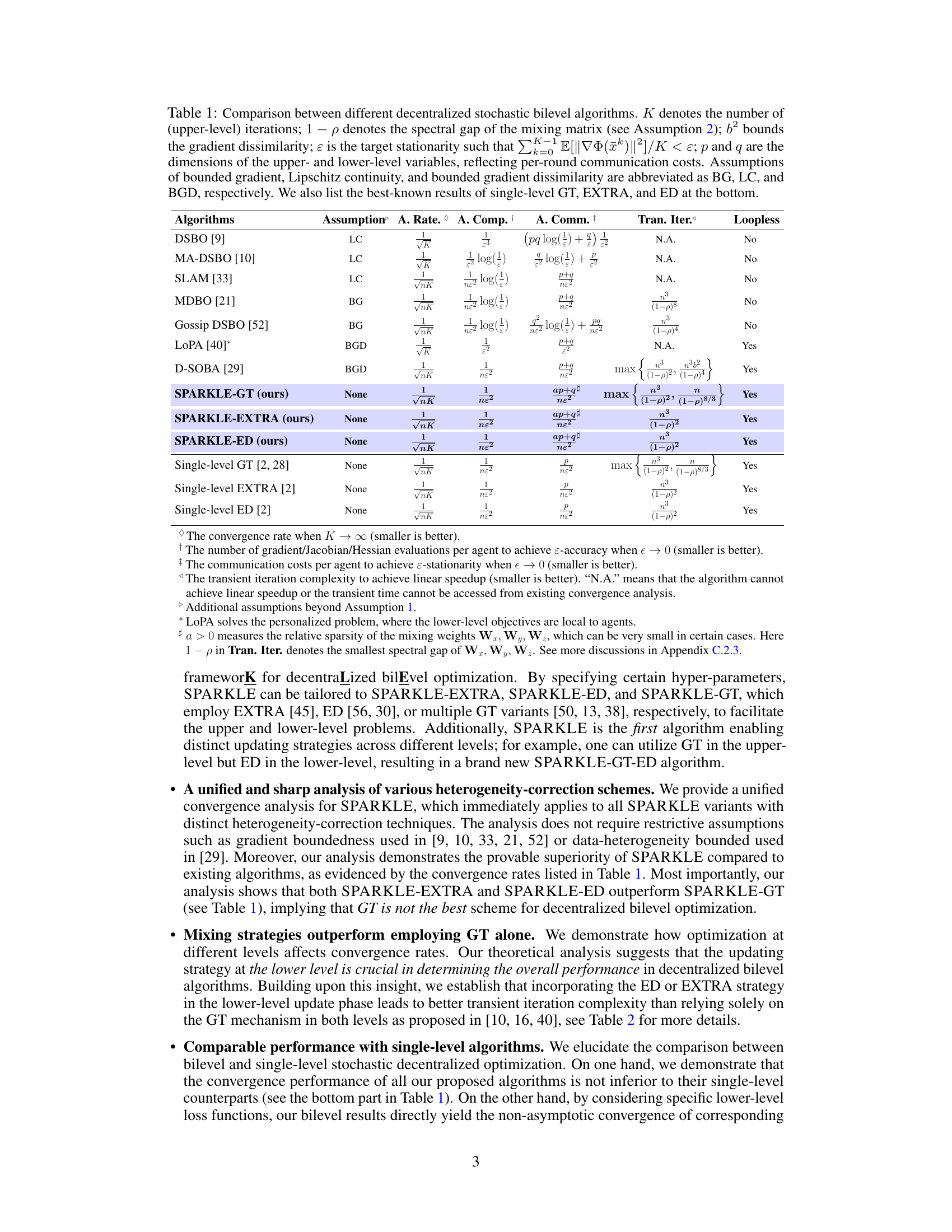
This figure displays the test accuracy achieved by different decentralized stochastic bilevel optimization algorithms on a hyper-cleaning task with varying corruption rates (p = 0.1, 0.2, 0.3). The algorithms compared include various versions of SPARKLE (using Gradient Tracking, EXTRA, and Exact Diffusion), as well as D-SOBA, MA-DSBO-GT, and MDBO. The plots show how the test accuracy changes over the number of gradient evaluations for each algorithm and corruption level. The results demonstrate that SPARKLE generally outperforms the other algorithms, and different strategies are suitable under different corruption rate.
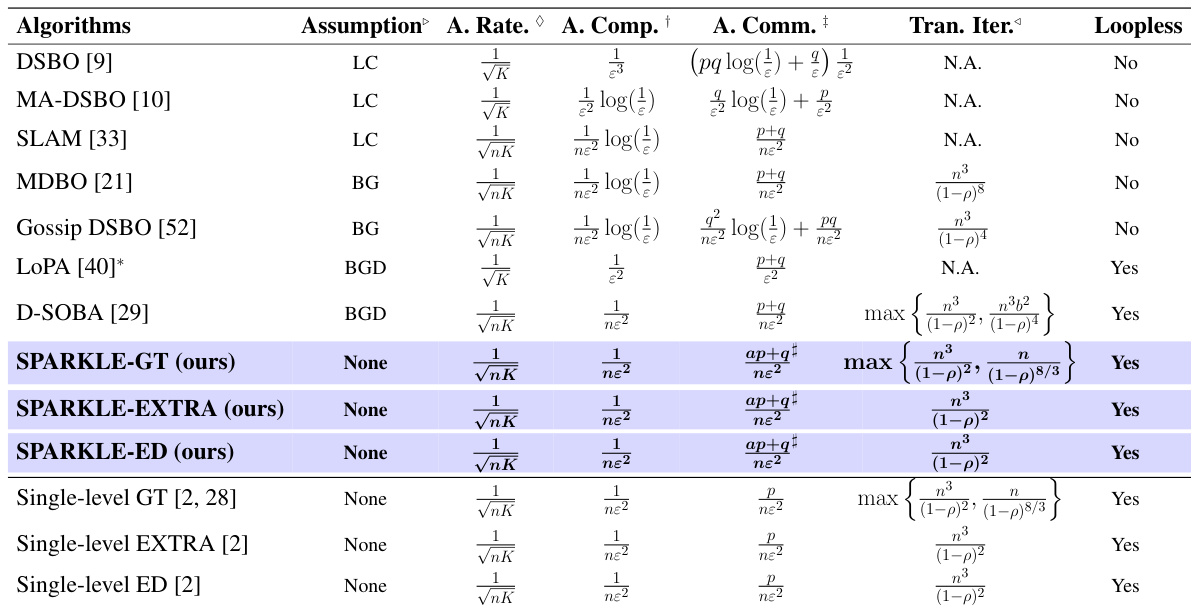
This table compares various decentralized stochastic bilevel optimization algorithms. It shows the convergence rate, computational complexity, communication cost, and transient iteration complexity for each algorithm. Assumptions made by each algorithm (bounded gradient, Lipschitz continuity, bounded gradient dissimilarity) are also listed, along with whether the algorithm is loopless. The table also includes comparisons to state-of-the-art single-level algorithms for context.
In-depth insights#
Decentralized Bilevel#
Decentralized bilevel optimization presents a unique challenge by combining the complexities of bilevel programming with the distributed nature of decentralized systems. Data heterogeneity across agents becomes a significant hurdle, requiring robust techniques beyond simple gradient tracking, such as EXTRA or Exact Diffusion, to ensure convergence. The nested optimization structure necessitates careful consideration of distinct update strategies for the upper and lower levels, potentially employing different heterogeneity-correction methods for each to optimize performance. A unified framework offering this flexibility and supporting a convergence analysis applicable to various combinations of techniques is highly desirable. The key is finding a balance between communication overhead and convergence speed, particularly in scenarios with limited bandwidth or high latency. Understanding the impact of network topology at different optimization levels is crucial, as is analyzing transient iteration complexity to assess the efficiency of achieving linear speedup.
SPARKLE Framework#
The SPARKLE framework, a unified single-loop primal-dual algorithm, presents a significant advancement in decentralized bilevel optimization. Its key strength lies in its flexibility: it unifies various heterogeneity-correction techniques (like Gradient Tracking, EXTRA, and Exact Diffusion) and allows for distinct strategies at the upper and lower levels, optimizing for different problem characteristics. This adaptability is crucial because bilevel problems often present unique challenges at each level. The framework’s unified convergence analysis covers all these variants, offering state-of-the-art convergence rates. Importantly, the analysis demonstrates the superiority of EXTRA and Exact Diffusion over Gradient Tracking for decentralized bilevel optimization, a valuable insight often overlooked. The framework also shows that mixed strategies, applying different techniques to different levels, offer substantial performance gains compared to using a single method across the board. This makes SPARKLE a powerful and versatile tool for addressing complex decentralized bilevel optimization problems that arise in many modern machine learning tasks.
Heterogeneity Methods#
In decentralized settings, data heterogeneity, where data distributions vary across agents, significantly impacts algorithm performance. Effective heterogeneity methods aim to mitigate this issue. Common approaches include gradient tracking, which aggregates gradients to reduce the influence of individual agent biases. Other techniques such as EXTRA (Exact Regularized dual Averaging) and Exact Diffusion offer alternative ways to correct for heterogeneity, often exhibiting faster convergence than gradient tracking. The choice of method can depend on factors such as network topology and the level of heterogeneity. A unified framework incorporating multiple heterogeneity correction methods might provide greater flexibility and potentially improved performance. Analysis of convergence rates for different methods under various conditions is crucial for selecting the most efficient approach for a given decentralized optimization problem. Future research could focus on exploring mixed strategies and adaptive methods that dynamically adjust to changing heterogeneity levels.
Convergence Analysis#
A rigorous convergence analysis is crucial for any optimization algorithm, and this is especially true for complex scenarios like decentralized bilevel optimization. A well-structured convergence analysis would typically begin by stating the assumptions made about the problem, such as smoothness and strong convexity of the objective functions, and properties of the network topology. Then, it would proceed to establish convergence rates, showing how quickly the algorithm approaches the optimal solution. The rate would often be expressed in terms of the number of iterations or the amount of data processed. A key aspect to look for is whether the analysis accounts for the decentralized nature of the problem, especially how the algorithm handles data heterogeneity and communication delays between agents. Tight bounds on convergence rates are highly desirable, providing strong guarantees on the algorithm’s performance. Ideally, the analysis would demonstrate linear speedup, meaning the convergence time scales linearly with the number of agents. Finally, a robust convergence analysis should cover various scenarios and parameter choices, demonstrating the algorithm’s stability and effectiveness across different problem instances.
Future of SPARKLE#
The future of SPARKLE, a decentralized bilevel optimization framework, is promising. Extending its applicability to more general non-convex upper-level problems is a crucial next step, as the current strong convexity assumption limits real-world use cases. Incorporating advanced variance reduction techniques could further accelerate convergence, particularly for large-scale datasets. Exploring alternative communication strategies beyond gradient tracking might offer significant advantages in terms of communication efficiency and robustness to network dynamics. Investigating the impact of varying network topologies on different levels of the optimization hierarchy warrants further investigation. Finally, empirical evaluations on diverse real-world applications, such as hyperparameter optimization in large language models, would validate SPARKLE’s effectiveness and pave the way for broader adoption. Benchmarking against the state-of-the-art centralized bilevel optimization algorithms would highlight the practical benefits of decentralized approaches.
More visual insights#
More on figures

This figure displays the test accuracy achieved by various SPARKLE-based algorithms (SPARKLE-GT, SPARKLE-EXTRA, SPARKLE-ED, SPARKLE-ED-GT, SPARKLE-EXTRA-GT) in comparison with other decentralized SBO algorithms (D-SOBA, MA-DSBO-GT, MDBO) on the FashionMNIST hyper-cleaning task. The x-axis represents the number of gradient evaluations, and the y-axis shows the test accuracy. Three different corruption rates (p = 0.1, 0.2, 0.3) are shown across three subfigures. It illustrates the superior performance of SPARKLE-EXTRA and SPARKLE-ED, and also demonstrates that using mixed strategies (ED/EXTRA with GT) can lead to similar accuracy compared with using ED or EXTRA only.
This figure compares the performance of four different decentralized stochastic bilevel optimization algorithms (D-SOBA, SPARKLE-GT, SPARKLE-ED, and SPARKLE-EXTRA) under various network topologies (fully connected, 2D torus, and adjusted ring) and levels of data heterogeneity (severe and mild). The y-axis represents the estimation error, while the x-axis represents the number of gradient evaluations. The results show that SPARKLE-ED and SPARKLE-EXTRA generally outperform D-SOBA and SPARKLE-GT across different network structures and heterogeneity levels, demonstrating their robustness and efficiency.

This figure compares the performance of four decentralized stochastic bilevel optimization algorithms (D-SOBA, SPARKLE-GT, SPARKLE-ED, and SPARKLE-EXTRA) across different network topologies (fully connected, 2D torus, and adjusted ring) and levels of data heterogeneity (severe and mild). The y-axis represents the estimation error (ΣNᵢ=₁||xᵢ(t) - x*||²), and the x-axis represents the number of gradient evaluations. The results illustrate the relative performance of these algorithms under varying network structures and data heterogeneity, highlighting the robustness of SPARKLE-ED and SPARKLE-EXTRA.
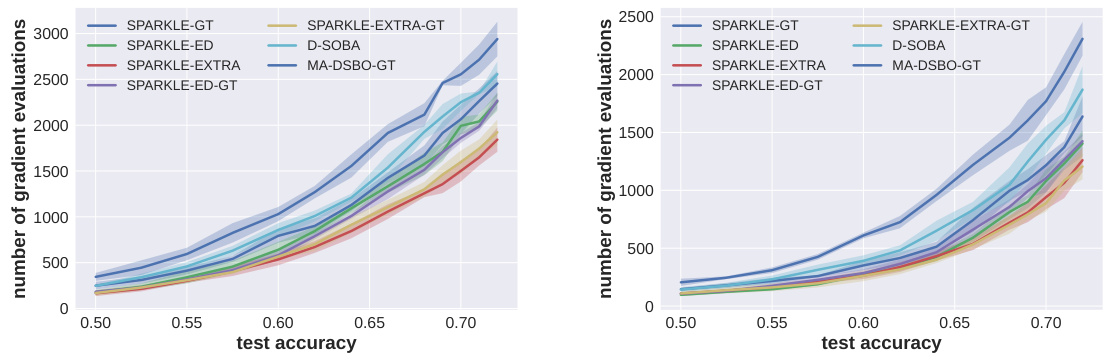
This figure shows the test accuracy achieved by various SPARKLE algorithms (SPARKLE-GT, SPARKLE-EXTRA, SPARKLE-ED, SPARKLE-ED-GT, and SPARKLE-EXTRA-GT) compared with other decentralized stochastic bilevel optimization algorithms (D-SOBA, MA-DSBO-GT, and MDBO) on the FashionMNIST dataset with different corruption rates (p = 0.1, 0.2, 0.3). The x-axis represents the number of gradient evaluations and the y-axis represents the test accuracy. Each plot corresponds to a specific corruption rate, showing the algorithms’ performance in data hyper-cleaning tasks under different levels of data corruption.
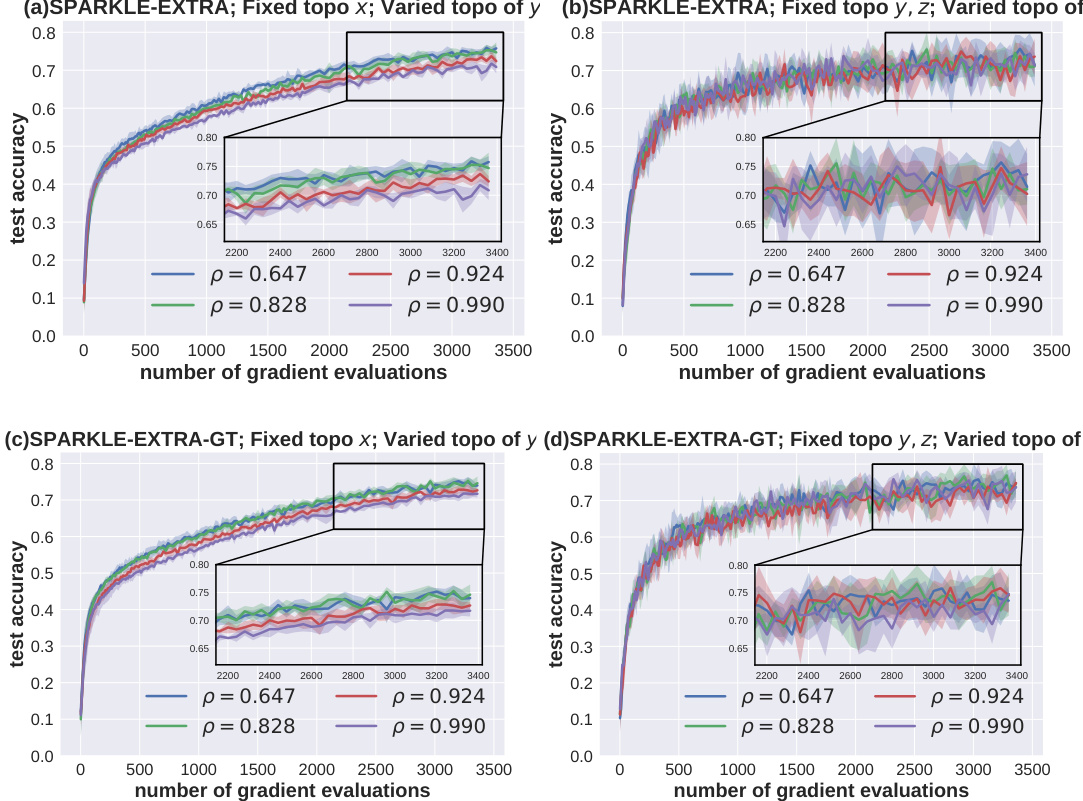
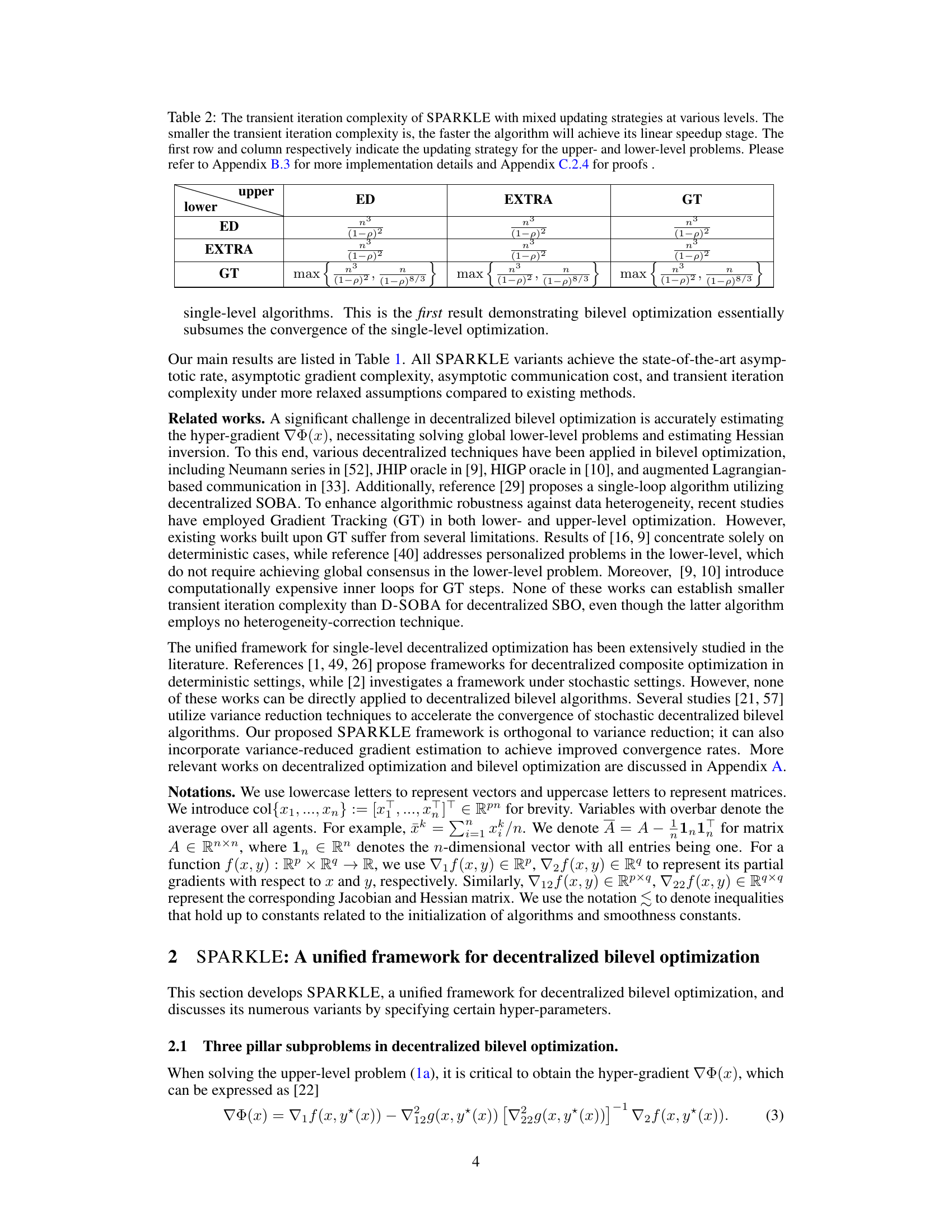
This figure shows the results of hyperparameter cleaning experiments on the FashionMNIST dataset. Two versions of the SPARKLE algorithm (EXTRA and EXTRA-GT) were tested with different communication strategies for updating the model parameters. In the first set of experiments, the upper level parameters (x) were updated using a fixed topology, while the lower level parameters (y, z) were updated using various topologies (different ring graphs). The second set of experiments reversed these settings: The lower level (y, z) used a fixed topology, while the upper level (x) employed various topologies. The results demonstrate that the performance is more sensitive to the topology of the lower level parameters (y, z) than to that of the upper level parameters (x).
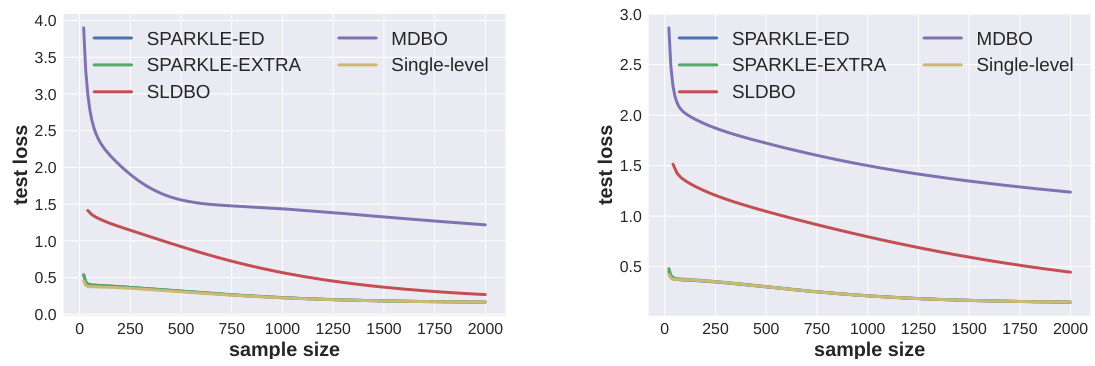
The figure shows the test loss for different decentralized bilevel optimization algorithms (SPARKLE-ED, SPARKLE-EXTRA, MDBO, SLDBO, and single-level ED) across various sample sizes (x-axis) for policy evaluation tasks. Two different network sizes are presented: n=10 (right panel) and n=20 (left panel). The test loss (y-axis) represents the average training loss over the last 500 iterations. The results highlight the convergence performance of different algorithms under varying data sizes and network configurations.

The figure shows the training and testing accuracy of SPARKLE-ED, D-SOBA, and Decentralized MAML on the meta-learning problem. It illustrates the performance of these algorithms over time, indicating the convergence and generalization abilities of each method. SPARKLE-ED demonstrates superior performance compared to the other two algorithms, achieving higher accuracy on both training and testing datasets.
More on tables

This table compares different decentralized stochastic bilevel optimization algorithms, highlighting their assumptions, convergence rates, computational and communication costs, and iteration complexity. It also includes the best-known results for single-level algorithms (GT, EXTRA, ED) for comparison.

This table compares different decentralized stochastic bilevel optimization algorithms. It shows their assumptions, convergence rates, computational and communication costs, and transient iterations. It also includes the best-known results for single-level algorithms for comparison.

This table compares various decentralized stochastic bilevel optimization algorithms, highlighting their assumptions, convergence rates, computational complexity, communication costs, and transient iterations. It also includes the best-known results for single-level algorithms (GT, EXTRA, and ED) for comparison.
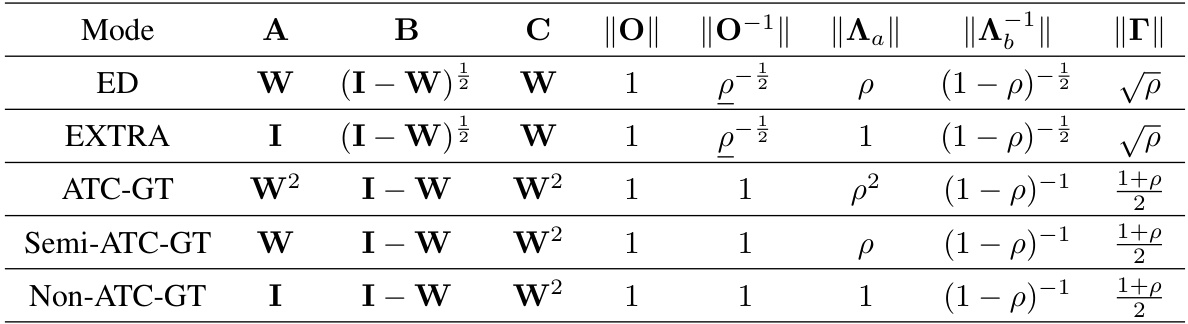
This table compares several decentralized stochastic bilevel optimization algorithms, highlighting their assumptions, convergence rates, computational complexity, communication costs, and transient iterations. It also includes the best known results for single-level algorithms (GT, EXTRA, and ED) for comparison.

This table compares different decentralized stochastic bilevel optimization algorithms, highlighting key characteristics such as assumptions, convergence rates, computational complexity (per round), communication costs, and transient iterations. It also includes the best-known results for single-level algorithms (GT, EXTRA, ED) for comparison.
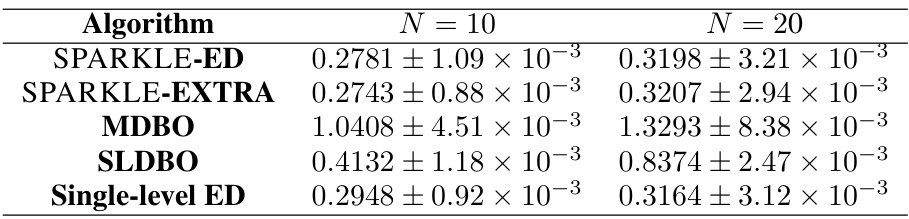
This table compares the performance of various decentralized stochastic bilevel optimization algorithms. It shows the convergence rate, computational complexity, communication cost, and transient iterations for each algorithm. Assumptions made by each algorithm are also specified, highlighting differences in algorithm requirements. The table also includes the best known results for single-level algorithms (Gradient Tracking, EXTRA, and Exact Diffusion) for comparison purposes.
Full paper#