Online Learning of Delayed Choices

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in online learning and choice modeling due to its novel approach to handling delayed feedback in dynamic settings. It provides robust algorithms with theoretical guarantees, addressing a significant limitation in existing methods. The work also opens new avenues for research in handling delayed feedback across various domains, with implications for e-commerce, advertising, and other decision-making applications.

Visual Insights

#

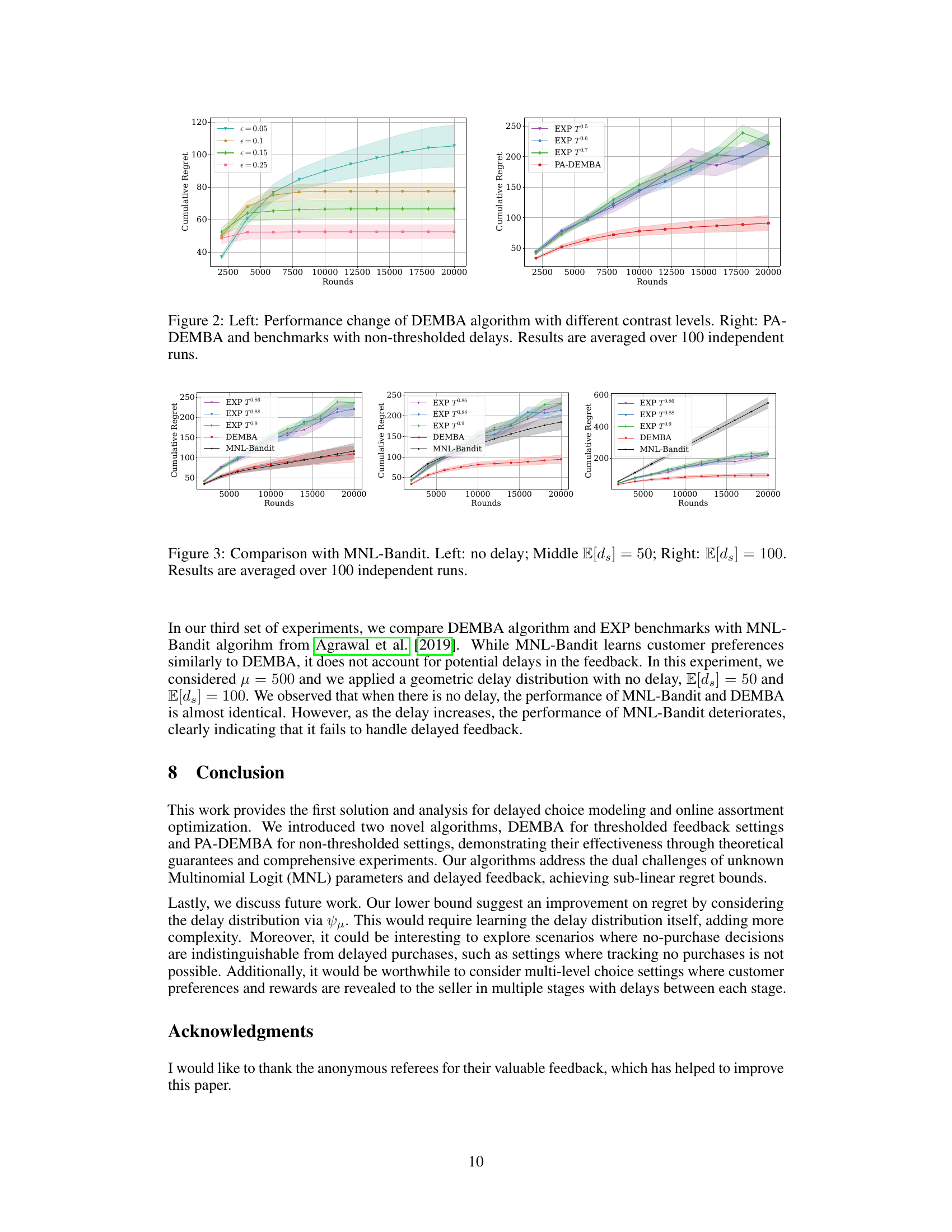
This figure displays the simulation results of the DEMBA algorithm and compares its performance against benchmark algorithms (EXP) under various settings. The top row shows the results with geometrically distributed delays, while the bottom row shows results for uniformly distributed delays. Each column represents different delay parameters (E[ds] and μ). The x-axis represents the number of rounds, and the y-axis represents the cumulative regret. The shaded areas represent the standard error over 100 independent runs.

This figure presents the simulation results of the DEMBA algorithm and compares its performance against benchmark algorithms under different delay settings. The top row shows results with geometrically distributed delays, while the bottom row displays results using uniformly distributed delays. Each column represents a different scenario with varying expected delay (E[ds]) and threshold (μ) for considering feedback. The results are averaged across 100 independent simulation runs, providing a robust comparison of the algorithms’ performance.

In-depth insights

#

Delayed Feedback

#

Delayed feedback, a prevalent challenge in online learning, significantly impacts the effectiveness of algorithms. The unpredictable nature of delays necessitates robust mechanisms for managing uncertainty. Traditional methods often assume immediate feedback, which makes them unsuitable for scenarios involving delayed responses. The impact of delayed feedback is multifaceted: it introduces bias into parameter estimations, leading to suboptimal decisions and increased regret. It complicates the exploration-exploitation balance; algorithms must carefully manage the tradeoff between gathering more information and acting on potentially outdated knowledge. Furthermore, censored feedback, where delayed information is discarded after a threshold, adds another layer of complexity, reducing the available data. To address this, effective online learning algorithms must incorporate strategies for handling the uncertainty of delayed feedback, such as incorporating confidence bounds and exploiting optimism. Successfully handling delayed feedback is crucial for improving performance in various applications, such as online advertising, and requires a thoughtful approach that integrates both theoretical analysis and practical considerations.

MNL Model

#

The Multinomial Logit (MNL) model is a powerful tool for choice modeling, particularly relevant in scenarios involving customer decisions among multiple alternatives, like those encountered in online advertising or product assortment optimization. Understanding consumer preferences is crucial for businesses to maximize revenue and engagement; MNL models provide a framework for this. The model’s versatility stems from its ability to estimate the probability of each choice option given the utilities associated with each option. However, the MNL model is not without limitations. Its assumption of independence of irrelevant alternatives (IIA) can be violated in real-world scenarios where the presence or absence of specific alternatives significantly alters the relative appeal of others. Therefore, careful consideration of this assumption is essential when applying the model. Furthermore, parameter estimation in the MNL model, often tackled using maximum likelihood estimation (MLE), can be computationally expensive and prone to issues of convergence. Handling unknown parameters and delayed feedback, as frequently observed in practical applications (such as online advertising), poses further challenges for the model. Algorithms like those discussed in the paper often need to balance exploration-exploitation strategies to deal with these issues. Despite these limitations, MNL models continue to be a cornerstone in choice modeling due to their ease of use and interpretability compared to more complex models.

Regret Analysis

#

A regret analysis in online learning, particularly within the context of a multinomial logit bandit (MNL-Bandit) problem with delayed feedback, is crucial for evaluating algorithm performance. It quantifies the difference between the rewards obtained by an algorithm and those achieved by an optimal strategy that has complete knowledge of the system. The analysis often involves deriving upper bounds on the cumulative regret, showing that the algorithm’s performance loss grows at a certain rate (e.g., sublinearly) with the number of interactions. This is important to ensure the algorithm learns effectively in the long run. A key challenge with delayed feedback is the need to manage bias in observations, which might lead to suboptimal decisions early on. The analysis would consider how this delay impacts the regret bound and explore techniques to mitigate the bias, such as censoring or incorporating delay models into the analysis. In addition to upper bounds, deriving matching lower bounds is essential to establish the tightness of the regret analysis, revealing the fundamental limits of performance for the considered problem. The analysis may also consider scenarios with thresholded delays (feedback is only considered if it’s received within a certain time window) and non-thresholded delays (all feedback is considered regardless of delay), investigating the impact of each on the regret. Ultimately, a thorough regret analysis provides crucial insights into algorithm efficiency and the effectiveness of exploration-exploitation strategies in dynamic environments with uncertain information arrival. The results would often be presented in big-O notation, showing how the regret scales with relevant parameters such as the number of products (N), time horizon (T), and delay characteristics.

Algorithm DEMBA

#

The DEMBA algorithm, designed for handling delayed feedback in multinomial logit bandit problems, is a significant contribution. It balances exploration and exploitation effectively using confidence bounds and optimism. The algorithm’s strength lies in its adaptability to thresholded feedback settings, where feedback is only considered within a specified timeframe. This is crucial for real-world applications where excessively delayed feedback might be irrelevant. The theoretical analysis provides regret bounds, showcasing the algorithm’s efficiency in learning customer preferences. The Õ(√NT) regret bound with a matching lower bound (up to a logarithmic term) demonstrates the algorithm’s efficiency in minimizing cumulative regret. However, the algorithm’s performance depends on several factors, including the delay distribution and threshold value, highlighting the need for further investigation into the impact of these parameters. Despite the robust theoretical foundation, empirical validation through experiments is crucial to assess the practical performance and robustness of DEMBA in diverse scenarios.

Future Research

#

The paper’s conclusion suggests several avenues for future research. Extending the model to handle more complex choice scenarios, such as those with context-dependent preferences or more intricate relationships between alternatives, is crucial. This involves moving beyond the basic multinomial logit model to incorporate richer representations of consumer choice behavior. Furthermore, investigating the impact of different delay distributions on learning algorithms is warranted, moving beyond simple geometric or uniform distributions to account for the real-world complexity of feedback arrival times. A deeper exploration of the algorithm’s robustness to various noise levels and data sparsity is necessary for practical applications. Finally, the authors highlight the importance of developing more efficient algorithms capable of handling larger-scale problems with potentially high dimensionality. This includes looking at the scalability of confidence bound methods and exploring alternative optimization techniques.

More visual insights

#

More on figures

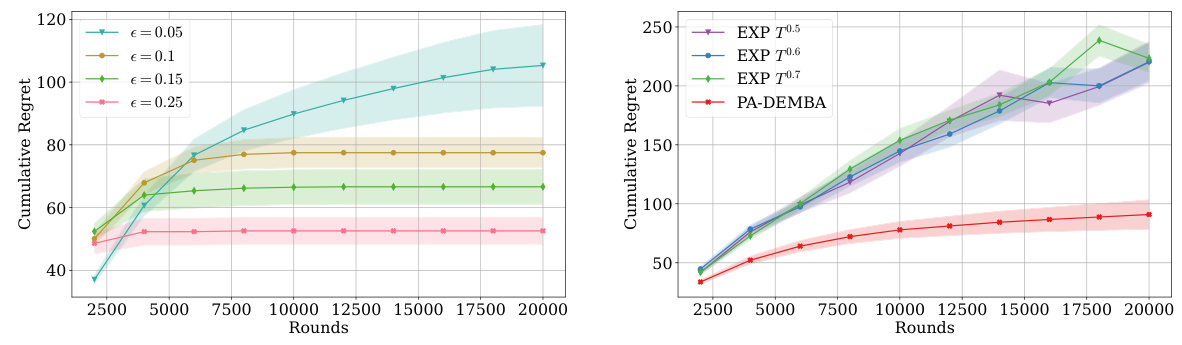
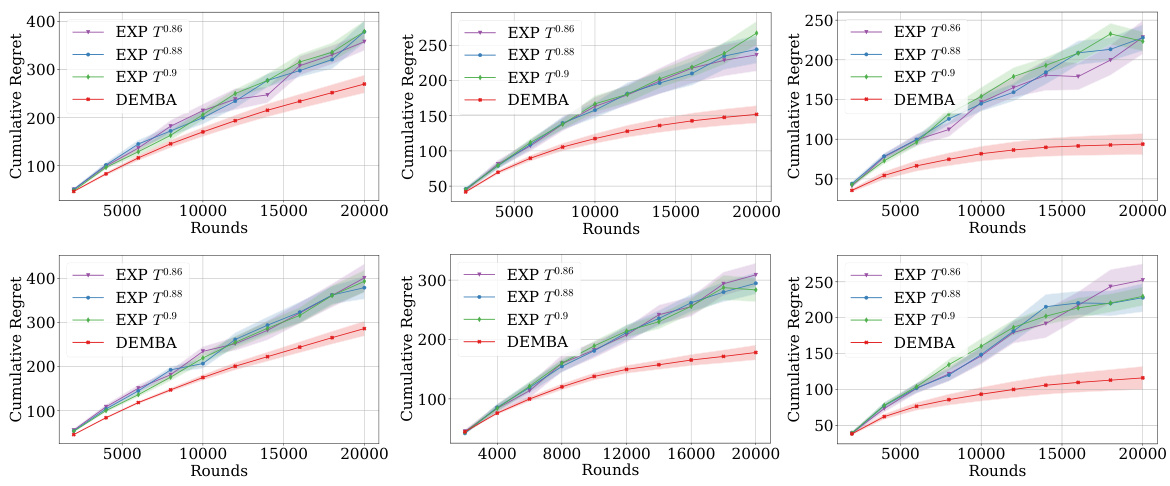
The left plot in Figure 2 shows how the performance of the DEMBA algorithm varies with different contrast levels (parameter ’e’). The contrast level affects the difficulty of distinguishing between products, and as expected, higher contrast makes learning easier. The right plot compares the performance of the PA-DEMBA algorithm (designed for non-thresholded delay settings) against benchmark algorithms. The shaded areas represent confidence intervals around the mean cumulative regret.

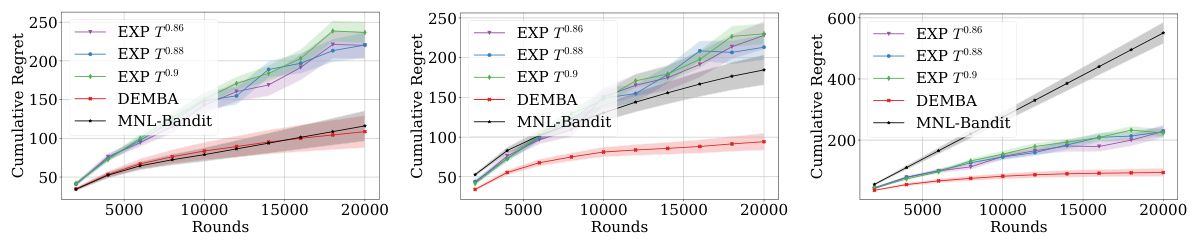
This figure compares the performance of the DEMBA algorithm against the MNL-Bandit algorithm and an explore-then-exploit (EXP) strategy under different delay conditions (no delay, E[ds] = 50, E[ds] = 100). The results show that DEMBA consistently outperforms the EXP strategy and is comparable to MNL-Bandit in the no-delay scenario, but significantly outperforms MNL-Bandit when delays are present, highlighting its effectiveness in handling delayed feedback.

Full paper

#