TL;DR#
Volume rendering in Neural Radiance Fields (NeRFs) is computationally expensive due to numerous calculations. Existing solutions often involve complex network modifications or new data structures. This significantly hinders real-time applications.
GL-NeRF tackles this challenge with a novel approach: it utilizes Gauss-Laguerre quadrature to significantly reduce the number of MLP calls required for volume rendering. This method is computationally inexpensive and requires minimal modifications to existing NeRF models; making it a simple yet efficient way to improve the speed of NeRF rendering without retraining the model. The results demonstrate a substantial increase in rendering speed with only a small drop in rendering quality. GL-NeRF represents a significant step towards real-time NeRF rendering and opens avenues for optimizing volume rendering in various applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in computer graphics and vision because it presents a novel, training-free method to significantly speed up neural radiance field (NeRF) rendering. GL-NeRF’s plug-and-play nature allows easy integration into existing NeRF models, potentially revolutionizing real-time rendering applications and opening new avenues for efficient volume rendering techniques.
Visual Insights#

🔼 This figure compares the sampling strategies of traditional NeRF and the proposed GL-NeRF. The left panel illustrates NeRF’s uniform sampling along a ray, resulting in many MLP calls (red dots) to determine the color of each sample point. In contrast, GL-NeRF (right panel) uses the Gauss-Laguerre quadrature to strategically select fewer sample points (blue dots) along the ray. This results in a significant reduction in MLP calls while maintaining rendering quality.
read the caption
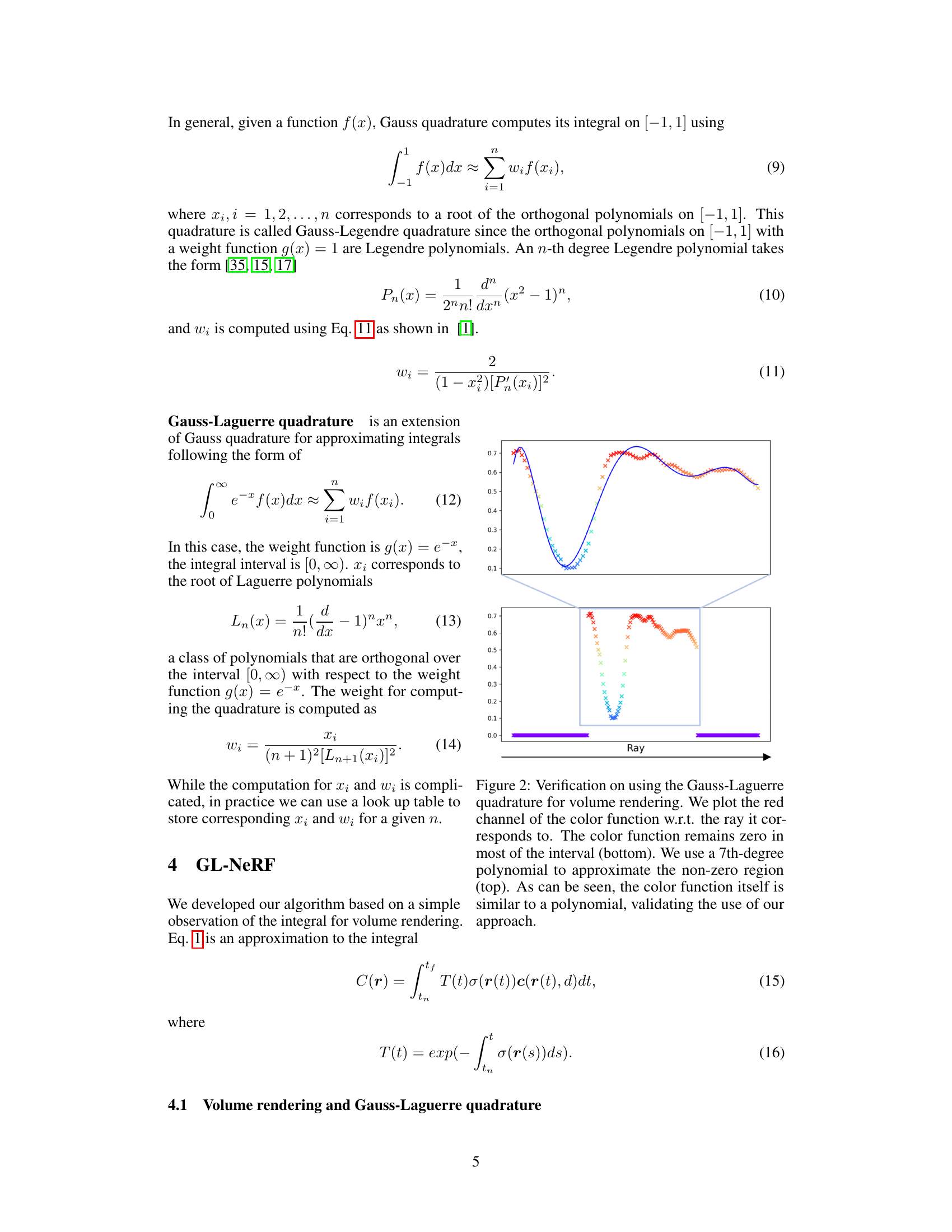
Figure 1: GL-NeRF method overview. The vanilla volume rendering in NeRF requires uniform sampling in space. This leads to a huge number of computationally heavy MLP calls since we have to assign each point a color value. Our approach, GL-NeRF, significantly reduces the number of points needed for volume rendering and selects points in the most informative area.

🔼 This table presents the weights (wi) and points (xi) used in the Gauss-Laguerre quadrature for volume rendering when n is set to 8. These values are used in the GL-NeRF algorithm to efficiently approximate the volume rendering integral. The weights represent the contribution of each point to the final rendered color, while the points determine the locations along a ray where the color is sampled. The table is crucial for implementing GL-NeRF’s deterministic point selection strategy, significantly reducing the computational cost compared to uniform sampling methods.
read the caption
Table 1: Gauss-Laguerre quadrature look-up table when n = 8.
In-depth insights#
GL-NeRF Overview#
GL-NeRF, or Gauss-Laguerre Neural Radiance Fields, offers a novel approach to accelerate NeRF volume rendering without requiring retraining or additional neural networks. Its core innovation lies in leveraging Gauss-Laguerre quadrature to efficiently approximate the volume rendering integral. This technique significantly reduces the number of computationally expensive MLP calls needed, as it strategically selects a smaller subset of points along each ray for color evaluation. The method is particularly effective because it focuses sampling on the most visually significant regions of the volume, leading to speedups while maintaining comparable rendering quality. The plug-and-play nature of GL-NeRF allows easy integration into existing NeRF models, making it a practical and powerful enhancement for improving the efficiency of NeRF-based applications. However, the effectiveness depends on how well the color function can be approximated by a polynomial, which introduces limitations. Despite this, GL-NeRF’s training-free nature and significant computational savings make it a promising technique for accelerating NeRF rendering in various applications.
Quadrature’s Role#
The core idea revolves around using Gauss-Laguerre quadrature to significantly accelerate neural radiance field (NeRF) rendering. Traditional NeRFs rely on numerous computations along each ray, making rendering slow. This method cleverly transforms the volume rendering integral into a form perfectly suited for Gauss-Laguerre quadrature, drastically reducing the number of required sample points. This approach offers a training-free, plug-and-play acceleration, meaning it can be easily integrated into existing NeRF models without retraining, demonstrating efficiency and simplicity. The quadrature’s role is pivotal in achieving this significant speedup, trading minor quality for massive performance gains. The accuracy of the quadrature in approximating the integral is key to the method’s success, making the choice of Gauss-Laguerre, with its specific properties, a critical design decision.
Point Selection#
The core concept of point selection in this research revolves around efficiently sampling points along a ray for volume rendering in neural radiance fields. Traditional methods uniformly sample points, leading to redundant computations. In contrast, this paper leverages the Gauss-Laguerre quadrature, a numerical integration technique, to selectively choose informative points. This approach stems from transforming the volume rendering integral into an exponentially weighted integral, ideally suited for Gauss-Laguerre quadrature. The quadrature’s strength lies in its ability to achieve high precision with minimal samples. Thus, point selection in GL-NeRF becomes a deterministic strategy, directly computing points corresponding to the roots of Laguerre polynomials, rather than random sampling. This deterministic selection focuses on the most visually impactful regions near the scene’s surface, optimizing computational efficiency without significant loss of visual quality. The method’s elegance is highlighted by its training-free nature and ease of integration into existing NeRF models, marking a significant advancement in efficient volume rendering.
Performance Gains#
Analyzing performance gains in a research paper requires a multifaceted approach. A simple speedup factor, while useful, doesn’t fully capture the trade-offs. We need to consider what aspects of performance improved (speed, memory usage, energy efficiency), and whether these gains came at the cost of accuracy or other metrics. Qualitative analysis of the results is crucial alongside quantitative data. Did the improvements significantly alter the usability or practicality of the approach? For instance, a method that’s 10x faster but only works on a subset of datasets is less impactful than a 2x improvement that applies broadly. The generalizability of the performance improvements is key: are the gains consistent across various datasets, model architectures, and hardware configurations? Finally, a discussion of the limitations and potential drawbacks of achieving these gains—such as increased complexity or reduced flexibility—is needed for a comprehensive understanding of their significance.
Future Works#
Future work could explore several promising avenues. Extending GL-NeRF to handle more complex scene geometries and dynamic scenes would significantly broaden its applicability. Investigating alternative quadrature methods beyond Gauss-Laguerre, potentially tailored to specific scene characteristics, could further enhance efficiency and accuracy. A thorough comparison against state-of-the-art acceleration techniques, including those employing advanced data structures or neural network architectures, is crucial for a robust evaluation of GL-NeRF’s performance benefits. Integrating GL-NeRF into existing real-time rendering pipelines is another important step, as it would bridge the gap between research and practical applications. Finally, studying the impact of different density estimation methods on GL-NeRF’s performance warrants attention, and could lead to novel optimization strategies for rendering speed and quality.
More visual insights#
More on figures
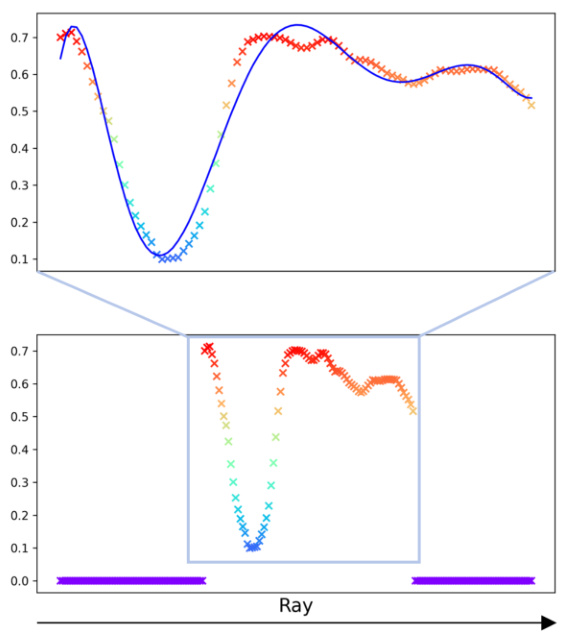
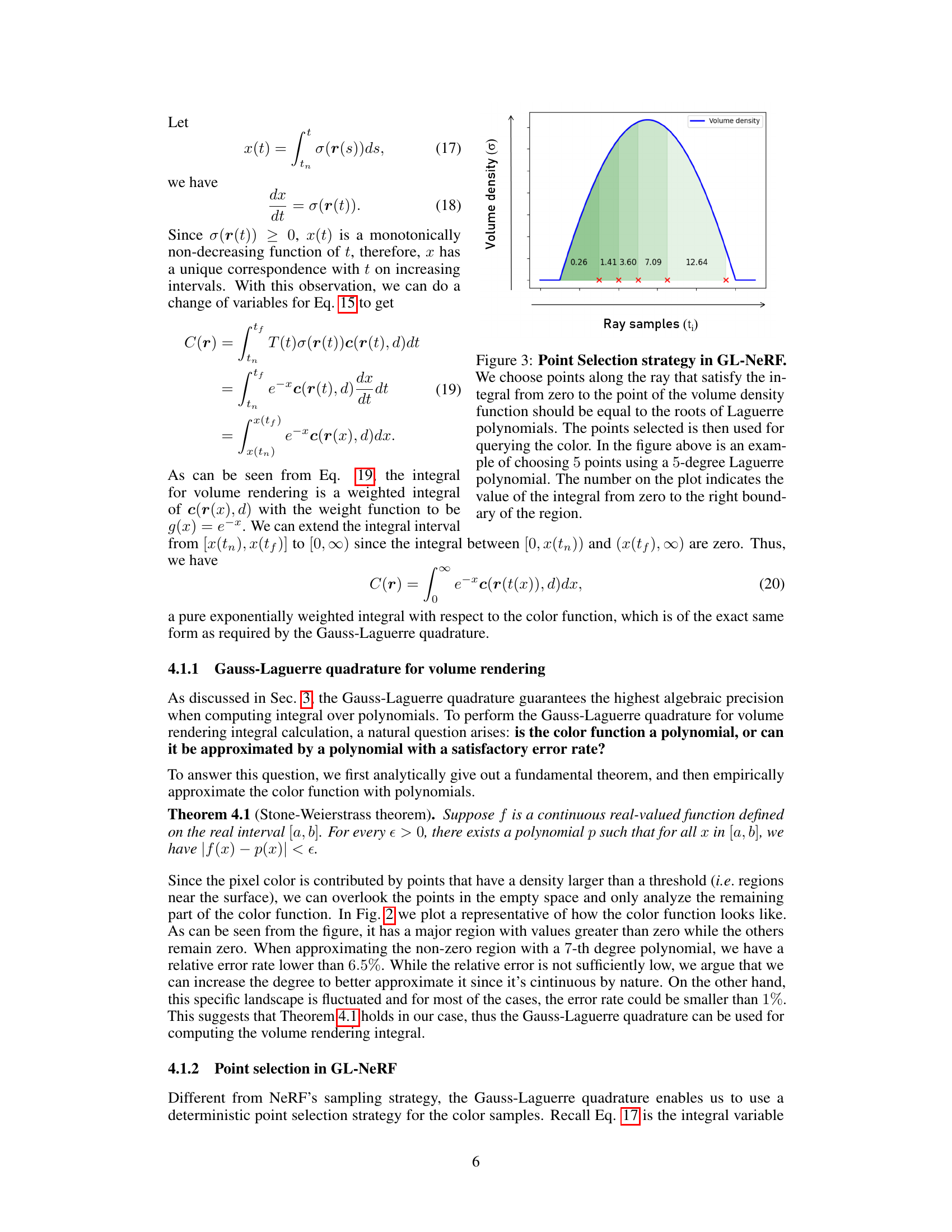
🔼 This figure illustrates the point selection strategy employed by GL-NeRF. Instead of uniform sampling, GL-NeRF strategically selects points along a ray based on the Gauss-Laguerre quadrature. The selection ensures that the integral of the volume density from the ray origin to each selected point corresponds to the roots of a Laguerre polynomial. This results in fewer points being evaluated, leading to computational savings. The plot shows an example of selecting 5 points using a 5th-degree Laguerre polynomial.
read the caption
Figure 3: Point Selection strategy in GL-NeRF. We choose points along the ray that satisfy the integral from zero to the point of the volume density function to be equal to the roots of Laguerre polynomials. The points selected is then used for querying the color. In the figure above is an example of choosing 5 points using a 5-degree Laguerre polynomial. The number on the plot indicates the value of the integral from zero to the right boundary of the region.
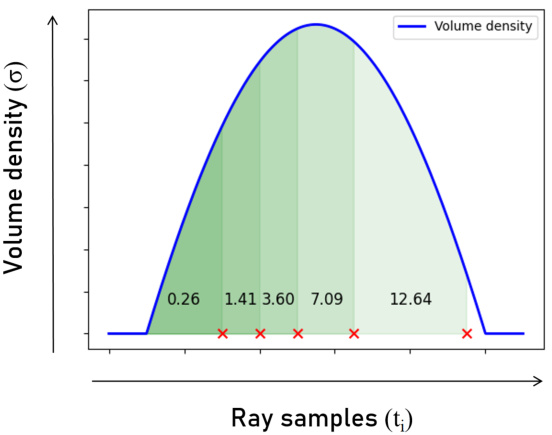
🔼 This figure illustrates the point selection strategy employed by GL-NeRF. Unlike traditional NeRF methods that use uniform sampling along a ray, GL-NeRF strategically selects points based on the roots of Laguerre polynomials. The selection is guided by the cumulative integral of the volume density, ensuring that points most informative for color reconstruction are chosen. The figure shows an example with 5 points chosen corresponding to a 5th degree Laguerre polynomial, highlighting how the integral value increases as points approach the object’s surface. The numbers shown on the plot represent the cumulative integral of the volume density up to each chosen point.
read the caption
Figure 3: Point Selection strategy in GL-NeRF. We choose points along the ray that satisfy the integral from zero to the point of the volume density function equal to the roots of Laguerre polynomials. The points selected is then used for querying the color. In the figure above is an example of choosing 5 points using a 5-degree Laguerre polynomial. The number on the plot indicates the value of the integral from zero to the right boundary of the region.

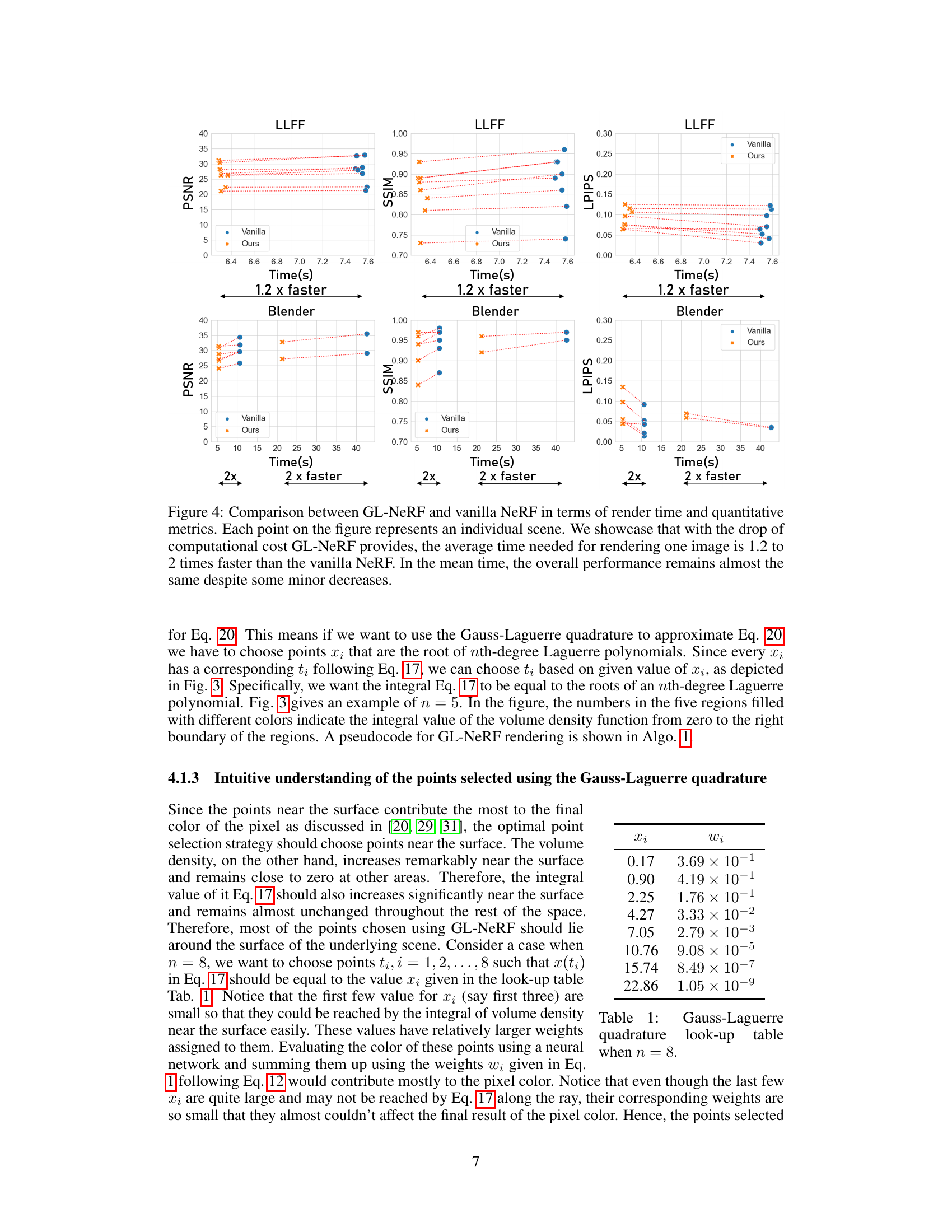
🔼 This figure compares the rendering time and quantitative metrics (PSNR, SSIM, LPIPS) of GL-NeRF against vanilla NeRF across multiple scenes from the LLFF and Blender datasets. The results demonstrate a 1.2x to 2x speedup in rendering time with GL-NeRF while maintaining comparable image quality, showing that GL-NeRF achieves significant computational savings without a substantial drop in performance.
read the caption
Figure 4: Comparison between GL-NeRF and vanilla NeRF in terms of render time and quantitative metrics. Each point on the figure represents an individual scene. We showcase that with the drop of computational cost GL-NeRF provides, the average time needed for rendering one image is 1.2 to 2 times faster than the vanilla NeRF. In the mean time, the overall performance remains almost the same despite some minor decreases.
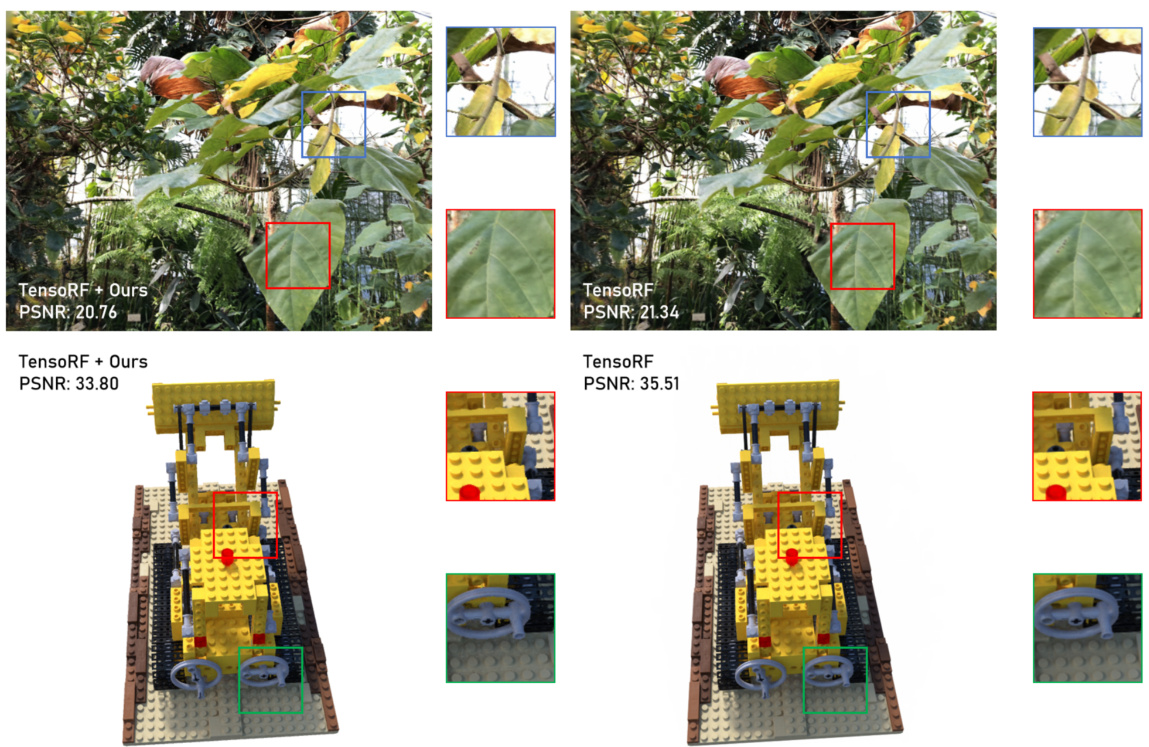
🔼 This figure displays qualitative comparisons of image rendering results between the original TensoRF model and the proposed GL-NeRF method, applied to two datasets: LLFF (top) and NeRF-Synthetic (bottom). The results demonstrate that while GL-NeRF reduces computational cost, there is only a minimal impact on the visual quality of the rendered images.
read the caption
Figure 5: Qualitative results on LLFF (top) and NeRF-Synthetic (bottom) datasets. We could tell from the comparisons that the drop in performances has minimal effect on the visual quality.

🔼 This figure compares the sampling strategies of vanilla NeRF and GL-NeRF. Vanilla NeRF uses uniform sampling, resulting in many MLP calls to determine the color of each point. GL-NeRF, in contrast, uses Gauss-Laguerre quadrature to select fewer, more informative points, thus significantly reducing the computational cost.
read the caption
Figure 1: GL-NeRF method overview. The vanilla volume rendering in NeRF requires uniform sampling in space. This leads to a huge number of computationally heavy MLP calls since we have to assign each point a color value. Our approach, GL-NeRF, significantly reduces the number of points needed for volume rendering and selects points in the most informative area.
More on tables
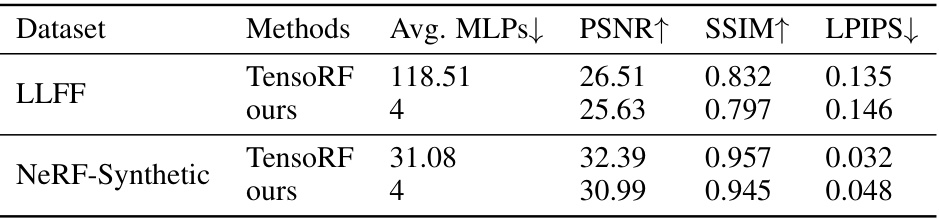
🔼 This table presents a quantitative comparison between TensoRF and GL-NeRF. It shows the average number of MLP calls (a measure of computational cost) and the resulting PSNR, SSIM, and LPIPS scores for both methods on the LLFF and NeRF-Synthetic datasets. The key finding is that GL-NeRF achieves a substantial reduction in MLP calls with only a minimal drop in the quality metrics (PSNR, SSIM, LPIPS), indicating significant computational savings without significant loss of image quality.
read the caption
Table 2: Quantitative comparison. We demonstrate that our method has a minimal performance drop while significantly reducing the number of color MLP calls.
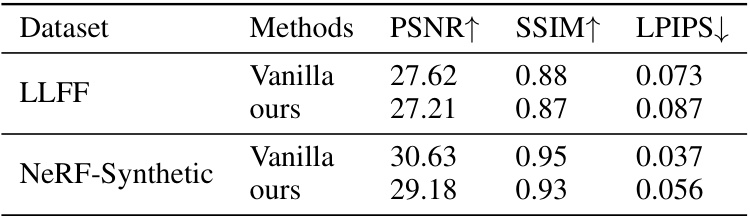
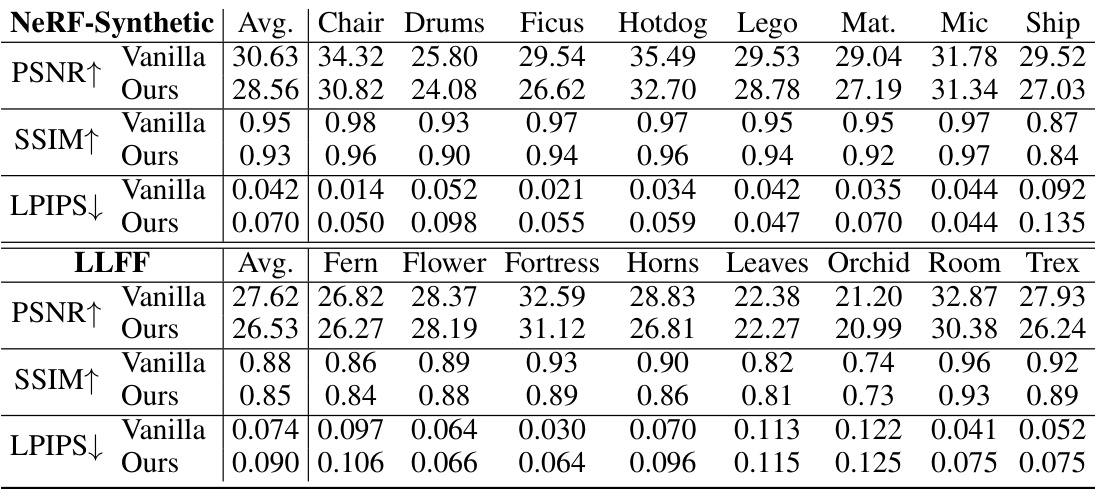
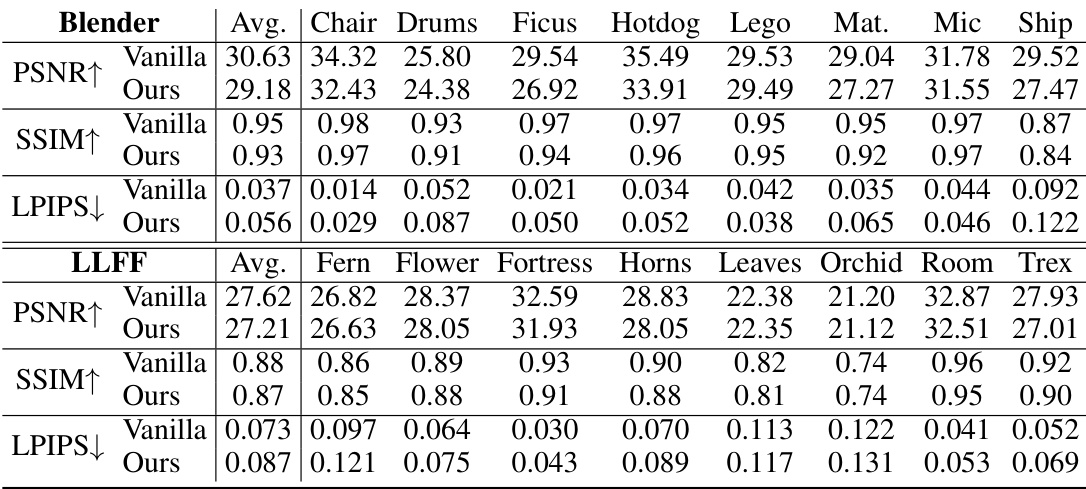
🔼 This table compares the quantitative metrics (PSNR, SSIM, LPIPS) of vanilla NeRF and GL-NeRF on LLFF and NeRF-Synthetic datasets. Vanilla NeRF uses more than 100 sampling points, while GL-NeRF uses only 32 points. The comparison highlights GL-NeRF’s ability to achieve comparable performance with significantly fewer sampling points.
read the caption
Table 3: Quantitative comparison when training with GL-NeRF. Vanilla refers to the vanilla NeRF and its sampling strategy while ours refers to replacing the fine sample stage in vanilla NeRF with our sampling strategy, i.e. GL-NeRF. The result for Vanilla NeRF is produced by rendering using more than 100 points while GL-NeRF only uses 32 points.
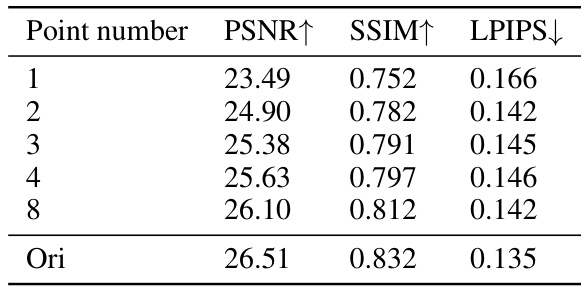
🔼 This table shows the results of an ablation study on the number of points sampled using the proposed GL-NeRF method. It compares the performance (PSNR, SSIM, LPIPS) of the method using different numbers of points (1, 2, 3, 4, 8) against the original TensoRF sampling strategy (‘Ori’). The results demonstrate that even with a relatively small number of points (8), GL-NeRF achieves performance comparable to the original method.
read the caption
Table 4: Ablation study on the number of points sampled. The more points we have, the better the performance will be. With 8 points, our method is comparable to the original sampling strategy in TensoRF.

🔼 This table compares the per-scene performance of InstantNGP and the proposed GL-NeRF method on the Blender dataset. It showcases the PSNR values achieved by each method for various scenes within the dataset. The results highlight that GL-NeRF can be easily integrated into existing NeRF models without significant performance loss.
read the caption
Table 5: Per-scene results on Blender dataset between InstantNGP and ours. We demonstrate that GL-NeRF is able to be plugged into ANY NeRF models.
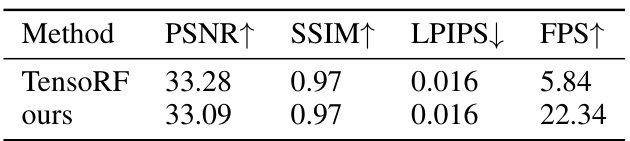
🔼 This table compares the performance of GL-NeRF and TensoRF on a Lego scene rendered using a WebGL-based renderer. It shows that GL-NeRF achieves a significant speedup (22.34 FPS vs 5.84 FPS) while maintaining comparable image quality (PSNR, SSIM, LPIPS). The experiment was conducted using an AMD Ryzen 9 5900HS CPU.
read the caption
Table 6: Comparison between our method and TensoRF on Lego scene using WebGL-based renderer. The result is collected from an AMD Ryzen 9 5900HS CPU. GL-NeRF is able to provide almost real-time rendering while remaining similar quality as TensoRF.
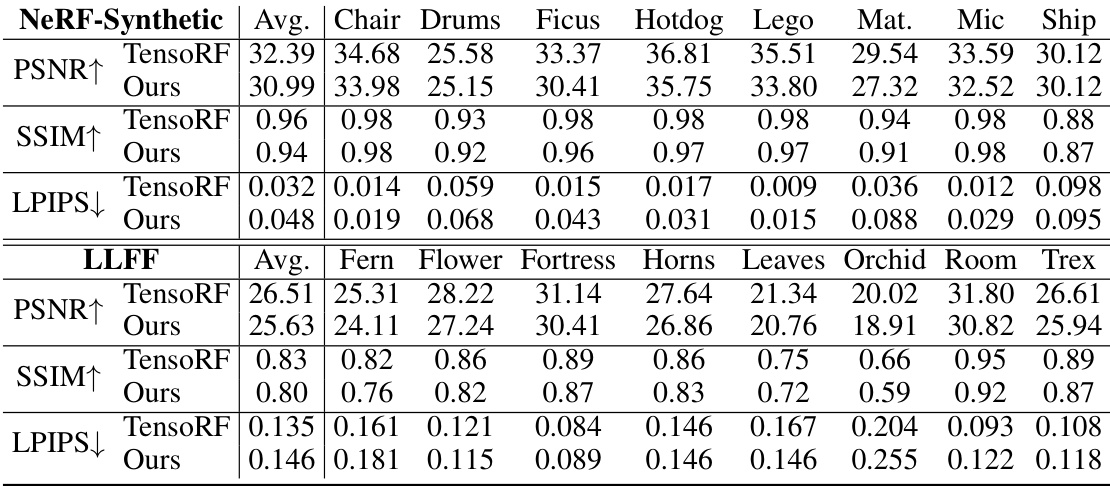
🔼 This table presents a quantitative comparison of the proposed GL-NeRF method against the baseline TensoRF method across two datasets: LLFF and NeRF-Synthetic. The comparison focuses on the average number of multi-layer perceptron (MLP) calls required for color prediction, peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and learned perceptual image patch similarity (LPIPS). The results show that GL-NeRF achieves comparable PSNR, SSIM, and LPIPS scores while significantly reducing the number of MLP calls, indicating improved computational efficiency.
read the caption
Table 2: Quantitative comparison. We demonstrate that our method has a minimal performance drop while significantly reducing the number of color MLP calls.
🔼 This table presents a quantitative comparison of the proposed GL-NeRF method against a baseline TensoRF model. It shows the average number of MLP calls, PSNR, SSIM, and LPIPS scores for both methods on the LLFF and NeRF-Synthetic datasets. The key takeaway is that GL-NeRF achieves a significant reduction in the number of MLP calls (from 118.51 to 4 on average) with only a minimal drop in performance metrics.
read the caption
Table 2: Quantitative comparison. We demonstrate that our method has a minimal performance drop while significantly reducing the number of color MLP calls.
🔼 This table presents a quantitative comparison of the proposed GL-NeRF method against a baseline TensoRF model. The comparison focuses on four key metrics: Average MLP calls, PSNR, SSIM, and LPIPS. The results show that GL-NeRF achieves a significant reduction in the number of MLP calls (from 118.51 to 4 for LLFF, and from 31.08 to 4 for NeRF-Synthetic) with only a minimal decrease in the other three performance metrics.
read the caption
Table 2: Quantitative comparison. We demonstrate that our method has a minimal performance drop while significantly reducing the number of color MLP calls.
Full paper#