TL;DR#
Large machine learning models struggle with communication bottlenecks when training and inference are distributed across multiple devices. Classical communication methods face limitations in terms of bandwidth and latency, especially as model size grows. Moreover, data privacy concerns become critical in such distributed settings. This necessitates the design of more efficient and secure distributed architectures.
This research introduces a framework for distributed computation using a quantum network, where data is encoded into quantum states. The authors demonstrate that, within this framework, inference and training using gradient descent requires exponentially less communication compared to classical methods. They show this advantage holds for specific graph neural networks, which are empirically evaluated on standard benchmarks. The quantum nature of communication also enhances privacy by limiting information extraction about data and model parameters.
Key Takeaways#
Why does it matter?#
This paper is crucial because it demonstrates exponential quantum communication advantages for distributed machine learning, a significant step toward more efficient and private AI systems. It opens new avenues for research in quantum algorithms and distributed computation, especially concerning large-scale models. The findings are relevant to current trends in large-scale machine learning and may reshape future distributed computing architectures.
Visual Insights#
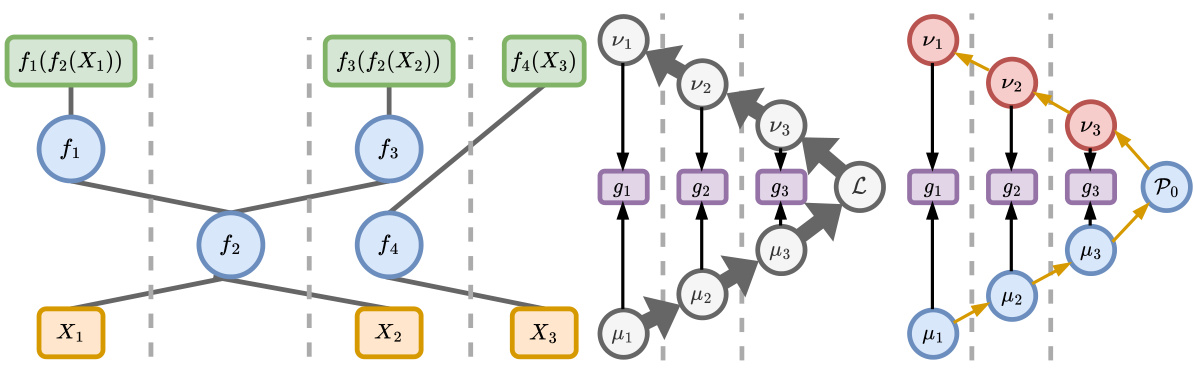
🔼 The figure illustrates a compositional distributed learning framework, where computations are divided among several devices connected via a network. The left panel shows a distributed computation graph, where each device is assigned a specific parameterized function that processes data and passes the result to other devices. The right panel depicts the pipelining method used for gradient calculation, comparing the classical and quantum communication costs. While classical communication is high in this process, the quantum approach significantly reduces the communication overhead.
read the caption
Figure 1: Left: Distributed, compositional computation. Dashed lines separate devices with computational and storage resources. The circular nodes represent parameterized functions that are allocated distinct hardware resources and are spatially separated, while the square nodes represent data (yellow) and outputs corresponding to different tasks (green). The vertical axis represents time. This framework of hardware allocation enables flexible modification of the model structure in a task-dependent fashion. Right: Computation of gradient estimators ge at different layers of a model distributed across multiple devices by pipelining. Computing forward features με and backwards features ve (also known as computing a forward or backward pass) requires a large amount of classical communication (grey) but an exponentially smaller amount of quantum communication (yellow). L is the classical loss function, and Po an operator whose expectation value with respect to a quantum model gives the analogous loss function in the quantum case.

🔼 This table shows the test accuracy for node classification and a decision problem on three datasets (Reddit, Cora, and OGBN-Products). Two models are compared: one using a PReLU activation function, and another using a second-degree polynomial. The results demonstrate that the polynomial model achieves comparable performance to the PReLU model, with only a minor reduction in accuracy.
read the caption
Table 1: Test Accuracy for Node Classification and Decision Problem. Replacing PRELU with a polynomial of degree 2 causes a slight reduction in accuracy (less than 1%) for both node classification and decision problem across all datasets.
In-depth insights#
Quantum Comm. Adv.#
The heading ‘Quantum Comm. Adv.’ likely refers to a section detailing the communication advantages offered by quantum computation in a distributed machine learning setting. The core idea revolves around leveraging quantum mechanics to transmit information more efficiently than classical methods, potentially leading to exponential speedups. This likely involves encoding data into quantum states, processing them across a quantum network, and extracting results with reduced communication overhead. The authors may present theoretical bounds proving this advantage and offer empirical evidence through simulations or experiments on benchmark datasets. The discussion may contrast this approach with classical communication methods and explore its potential impact on areas such as privacy and scalability in machine learning.
Graph Net Inference#
The section on ‘Graph Net Inference’ likely explores how graph neural networks (GNNs) can be adapted for efficient inference in a distributed or quantum computing setting. It probably demonstrates how GNNs’ compositional structure, which involves local message passing operations, aligns well with distributed computation frameworks. The key insight would likely center on how this compositional structure reduces the communication overhead compared to alternative approaches for distributed inference. This may involve proving exponential quantum communication advantages for certain classes of GNNs, demonstrating that quantum networks could facilitate dramatically faster inference for graph problems than classical networks. The authors likely present empirical evaluations, using standard graph datasets and benchmark tasks, to validate their theoretical results. Furthermore, the discussion would likely include a comparison of the performance of quantum GNN inference with existing classical counterparts. Focus is likely placed on the tradeoff between communication cost and computational complexity, demonstrating the conditions where quantum GNNs offer a significant advantage and discussing potential privacy implications of using quantum-based graph inference.
Expressivity of Models#
The expressivity of models is a crucial aspect of the research paper, focusing on the ability of the proposed quantum circuits to represent complex relationships within data. The authors investigate the expressivity of their compositional models, demonstrating that these models can efficiently approximate certain graph neural networks. This expressivity is shown to increase exponentially with model depth, which is a significant finding. Furthermore, they address the common misconception of linear restrictions in quantum neural networks, showcasing how their model can encode highly nonlinear features of their inputs. The research highlights exponential gains in expressivity, a crucial characteristic for handling complex data and achieving superior performance. The study not only validates their theoretical claims with empirical evidence through benchmark performance on standard datasets, but also opens doors for future work to delve deeper into the relationship between model architecture, data encoding, and overall expressivity, which could impact many machine learning applications.
Limitations of Approach#
A thoughtful analysis of a research paper’s limitations section requires considering several key aspects. First, identifying and clearly articulating the specific limitations is crucial. This means not only mentioning potential issues but also providing a nuanced explanation of their impact and scope. For instance, are there assumptions made that might not hold true in real-world scenarios? Does the methodology have inherent biases or constraints? It’s important to assess the generalizability of the findings; do they hold only under specific conditions? Furthermore, a rigorous evaluation necessitates discussing the methodological limitations, such as sample size, data quality, or the experimental design. The use of specific techniques or models might present further limitations and their shortcomings should be acknowledged. Quantifying the impact of these limitations wherever possible adds valuable depth, showing the practical implications of the limitations. Finally, proposing potential avenues for future research to address the identified limitations demonstrates forward-thinking and contributes to a complete analysis.
Future Research#
Future research directions stemming from this work could explore extending the quantum advantage to more complex models and broader classes of machine learning problems beyond graph neural networks. Investigating the practical implications of the identified privacy enhancements in realistic distributed settings is crucial. Further research should focus on developing efficient quantum algorithms for training larger and deeper quantum neural networks and addressing the scalability challenges for implementing and deploying these methods. Another important avenue is bridging the gap between theoretical results and practical implementations, requiring substantial work on developing efficient and fault-tolerant quantum hardware and software infrastructure. Finally, exploring the potential synergies between classical and quantum machine learning paradigms for distributed computation would open up exciting new possibilities for large-scale AI applications.
More visual insights#
More on figures
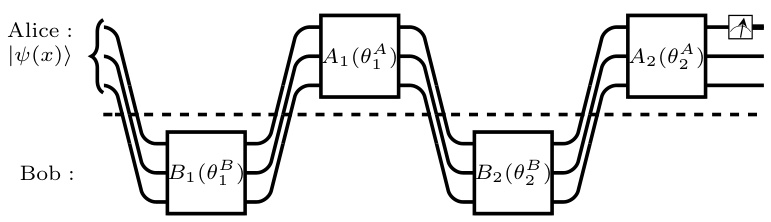
🔼 This figure shows a distributed quantum circuit for calculating the loss function (L) and its gradients with respect to the parameters of the unitaries (A and B). The circuit is composed of layers, with each layer involving a unitary operation performed by either Alice or Bob. The total communication required for estimating both L and its gradients is only polylogarithmic in the input size (N) and the number of parameters in each unitary (P), which is a significant improvement over classical methods.
read the caption
Figure 2: Distributed quantum circuit implementing L for L = 2. Both L and its gradients with respect to the parameters of the unitaries can be estimated with total communication that is polylogarithmic in the size of the input data N and the number of trainable parameters per unitary P.

🔼 This figure illustrates a compositional approach to distributed computation where separate devices handle different parts of a computation. The left panel shows the data flow in a compositional distributed computation, with nodes representing parameterized functions and data. The right panel depicts how gradient estimators can be computed via pipelining, showcasing the potential for quantum communication advantages. Quantum communication is shown in yellow and classical communication in grey, highlighting the potential exponential reduction in communication overhead using quantum methods.
read the caption
Figure 1: Left: Distributed, compositional computation. Dashed lines separate devices with computational and storage resources. The circular nodes represent parameterized functions that are allocated distinct hardware resources and are spatially separated, while the square nodes represent data (yellow) and outputs corresponding to different tasks (green). The vertical axis represents time. This framework of hardware allocation enables flexible modification of the model structure in a task-dependent fashion. Right: Computation of gradient estimators ge at different layers of a model distributed across multiple devices by pipelining. Computing forward features με and backwards features ve (also known as computing a forward or backward pass) requires a large amount of classical communication (grey) but an exponentially smaller amount of quantum communication (yellow). L is the classical loss function, and Po an operator whose expectation value with respect to a quantum model gives the analogous loss function in the quantum case.
More on tables

🔼 This table presents the test accuracy results for graph classification across multiple benchmark datasets. The results from the proposed model, SIGN (ours), are compared to several other state-of-the-art graph classification models, including GIN, DropGIN, DGCNN, U2GNN, HGP-SL, and WKPI. The table shows that the SIGN model achieves comparable performance across most datasets.
read the caption
Table 2: Graph Classification Test Accuracy. Our model achieves comparable results to GIN and other known models on most datasets (see full table in Table 5).

🔼 This table presents the results of node classification and decision problem experiments on three datasets: Reddit, Cora, and OGBN-Products. Two models are compared: one using a standard PRELU activation function and another using a second-degree polynomial activation function. The table shows that the polynomial model achieves comparable accuracy to the PRELU model, with only a small decrease (less than 1%) in performance.
read the caption
Table 1: Test Accuracy for Node Classification and Decision Problem. Replacing PRELU with a polynomial of degree 2 causes a slight reduction in accuracy (less than 1%) for both node classification and decision problem across all datasets.
🔼 This table presents the test accuracy results for node classification and a decision problem on three datasets (Reddit, Cora, and OGBN-Products). Two models are compared: SIGN with a PRELU activation function and SIGN with a second-degree polynomial activation function. The results show that replacing PRELU with a polynomial results in a small accuracy decrease (less than 1%).
read the caption
Table 1: Test Accuracy for Node Classification and Decision Problem. Replacing PRELU with a polynomial of degree 2 causes a slight reduction in accuracy (less than 1%) for both node classification and decision problem across all datasets.

🔼 This table compares the test accuracy of the proposed quantum graph neural network model against several other state-of-the-art graph classification models across multiple benchmark datasets. The results show that the proposed model achieves comparable or better accuracy than existing models on most datasets.
read the caption
Table 2: Graph Classification Test Accuracy. Our model achieves comparable results to GIN and other known models on most datasets (see full table in Table 5).
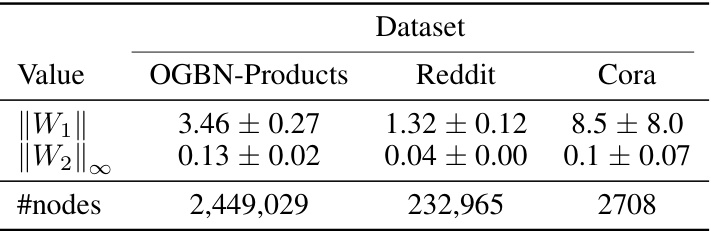
🔼 This table presents the test accuracy results for node classification and a derived decision problem on three datasets (Reddit, Cora, and OGBN-Products). Two model variants are compared: one using the PRELU activation function and another using a second-degree polynomial. The results show that the polynomial variant achieves comparable performance with only a negligible decrease in accuracy.
read the caption
Table 1: Test Accuracy for Node Classification and Decision Problem. Replacing PRELU with a polynomial of degree 2 causes a slight reduction in accuracy (less than 1%) for both node classification and decision problem across all datasets.
Full paper#



















