TL;DR#
Optimal control of large-scale dynamical systems is a crucial challenge in various fields, but traditional methods become computationally expensive as problem dimensions grow. This limitation necessitates the development of new, more efficient algorithms, especially those leveraging quantum computing’s potential for speedups. Existing quantum algorithms primarily address specific optimal control problems within quantum science, lacking a general solution for accelerating large-scale problems. This is a significant barrier for broader adoption and integration of quantum computing in engineering and related disciplines.
This paper introduces a novel end-to-end quantum algorithm for linear-quadratic control that significantly outperforms classical methods. The algorithm uses a policy gradient approach, incorporating a quantum subroutine for solving the Lyapunov equation. This innovative approach achieves a super-quadratic speedup compared to classical methods and demonstrates superior robustness and accuracy. The results offer strong evidence of the potential for quantum advantage in addressing complex, high-dimensional control problems, opening new possibilities in engineering design, industrial automation, and scientific research.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents the first end-to-end quantum algorithm for linear-quadratic control problems with provable speedups, addressing a critical need in handling the complexity of large-scale dynamical systems. Its super-quadratic speedup over classical methods is a major advancement, opening new avenues for quantum computing applications in various engineering and scientific domains. Furthermore, the algorithm’s robustness and efficiency are significant improvements that make it practical even in the early stages of fault-tolerant quantum computing. This work also pushes the boundaries of quantum reinforcement learning and numerical linear algebra, providing valuable insights for future research.
Visual Insights#

🔼 This figure illustrates the hybrid quantum-classical approach of the proposed algorithm. The classical module uses a gradient-based optimizer to iteratively update the control policy (K). This policy is then passed to the quantum module, which uses differentiable quantum computing techniques to evaluate the objective function f(K) via a quantum simulator. This process repeats, with the objective function evaluation providing feedback for the optimizer to refine the control policy until it converges to the optimal policy.
read the caption
Figure 1: Differentiable quantum computing for linear control.

🔼 This table compares the time/gate complexity of different methods for solving the linear-quadratic regulator (LQR) problem. It shows that the proposed quantum algorithm achieves a super-quadratic speedup compared to classical methods like the Schur method, Newton-Kleinman method, and classical policy gradient methods.
read the caption
Table 1: Asymptotic cost of different methods for LQR.
In-depth insights#
Quantum LQR#
A Quantum Linear Quadratic Regulator (Quantum LQR) algorithm promises to significantly speed up optimal control calculations for large-scale systems. Classical LQR methods often struggle with the computational cost of solving high-dimensional matrix equations. A quantum approach offers the potential to overcome this limitation, leveraging quantum algorithms for tasks like solving the matrix Lyapunov equation and performing gradient estimations more efficiently. The key innovation often involves creating a quantum-assisted differentiable simulator, enabling quicker and more accurate gradient calculations within a policy gradient framework. This approach is expected to provide a super-quadratic speedup over existing classical methods, which is a significant improvement for complex engineering problems. However, practical implementation would require access to sufficiently advanced quantum hardware and further work is needed to fully understand the scalability and robustness of these methods. The theoretical advantage is significant but requires further validation in practical settings and a deeper exploration of how it handles noise and uncertainties.
Policy Gradient#
Policy gradient methods are a cornerstone of reinforcement learning, offering a powerful approach to optimize control policies. In the context of linear-quadratic regulators (LQRs), policy gradients provide an elegant way to iteratively improve a controller by directly adjusting its parameters. The gradient, calculated using an analytical formula or approximated via stochastic methods, indicates the direction of steepest improvement in the performance metric. This paper leverages the policy gradient method to solve large-scale LQR problems. A key contribution lies in the development of a quantum-enhanced differentiable simulator. This simulator enables efficient gradient estimation, significantly accelerating the convergence to the optimal control policy. While classical methods often rely on stochastic approximation, this quantum approach improves both accuracy and robustness. The paper demonstrates a super-quadratic speedup compared to traditional methods, highlighting the potential of quantum computing for solving challenging control problems.
Quantum Speedup#
The concept of “Quantum Speedup” in the context of this research paper centers on the acceleration of solving linear-quadratic regulator (LQR) problems, a crucial task in controlling large-scale dynamical systems. Classical methods for LQR often face significant computational hurdles as system dimensions grow. This paper proposes a quantum algorithm that achieves a super-quadratic speedup compared to these classical techniques. The core of this speedup comes from a novel quantum subroutine for solving the matrix Lyapunov equation, a key component of LQR. The use of a quantum differentiable simulator for efficient gradient estimation enhances the accuracy and robustness of the method, furthering the quantum advantage. Provable speedups are demonstrated, marking a significant step toward practical quantum advantage in the field of optimal control.
Lyapunov Solver#
A Lyapunov solver is a crucial algorithm for solving the Lyapunov equation, a fundamental problem in systems and control theory. This equation arises in various applications, including stability analysis, control design, and model reduction. The efficiency of a Lyapunov solver is critical, especially when dealing with large-scale systems. Classical methods often suffer from high computational costs, scaling cubically with the system’s dimension. The paper explores a quantum approach offering a potential for significant speedup, particularly relevant for large-scale systems where classical methods struggle. The quantum algorithm leverages quantum linear algebra techniques to achieve a super-quadratic speedup compared to classical approaches. This quantum advantage is particularly important given the growing complexity of modern engineering designs and the demand for efficient solutions to large-scale optimal control problems.
Future of Control#
The future of control systems is likely to be shaped by several converging trends. Quantum computing offers the potential for significant speedups in solving complex control problems, especially those involving high-dimensional systems. Differentiable programming and machine learning techniques can enable more efficient and adaptive control strategies, potentially leading to more robust and autonomous systems. However, challenges remain, including developing efficient algorithms and dealing with the inherent noise in quantum systems. Furthermore, the integration of these new techniques into existing control frameworks needs to be further explored, paying attention to scalability, robustness, and explainability. Successfully addressing these issues will be crucial for enabling the full potential of quantum and AI-based control systems, leading to advancements across a wide range of industrial applications. Beyond computational enhancements, new theoretical frameworks are needed to guide the development of more sophisticated, powerful, and versatile control methodologies.
More visual insights#
More on figures
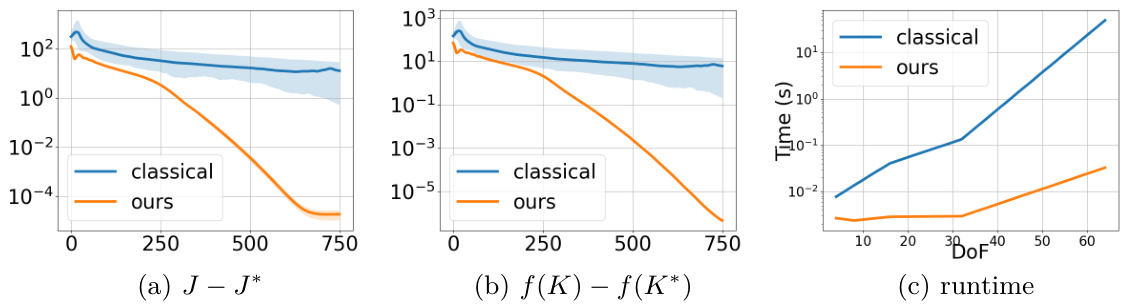
🔼 This figure compares the convergence speed of the proposed quantum policy gradient algorithm and the classical policy gradient method from [45] on a mass-spring-damper system. Three subplots show the convergence for the objective function (J - J*), the objective function expressed in terms of the feedback gain (f(K) - f(K*)), and the runtime. The results demonstrate that the quantum algorithm converges significantly faster than the classical approach, achieving a similar level of accuracy in fewer iterations and less computational time. The speedup becomes more pronounced as the system size increases, highlighted in the runtime subplot.
read the caption
Figure 2: Numerical Results on Convergence. Following the mass-spring-damper setup in [45], our policy gradient descent algorithm converges much faster than [45].

🔼 This figure compares the convergence speed of the proposed quantum policy gradient algorithm and a classical method for solving a linear quadratic regulator (LQR) problem applied to aircraft pitch angle control. The plots show that the proposed quantum algorithm achieves a much faster convergence rate than the classical method, highlighting the effectiveness of quantum computing for large-scale optimal control problems.
read the caption
Figure 3: Numerical Results on Convergence. In the aircraft control problem, our policy gradient descent algorithm converges much faster than classic method [45].
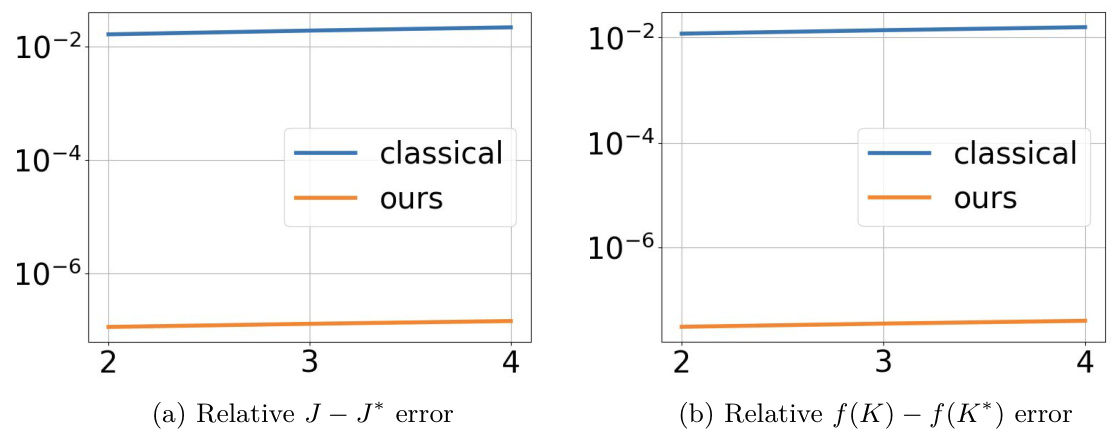
🔼 This figure shows the relative errors ((J - J*)/J* and (f(K) - f(K*))/f(K*)) for both the proposed quantum algorithm and a classical method [45] as the problem size (number of masses in a mass-spring system) increases from 2 to 4. The results demonstrate that the proposed quantum algorithm achieves smaller relative errors compared to the classical method as the problem size grows. This highlights the improved accuracy and robustness of the quantum algorithm, especially when dealing with larger-scale problems.
read the caption
Figure 4: Relative Error. We scale the size of a mass-spring system and our method consistently gets smaller relative error compared to [45].
Full paper#



















