↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning models struggle to generalize to data that differs from their training data (out-of-distribution or OOD data). This is a critical problem for deploying models in real-world settings where it’s expensive to get labeled data. Recent research showed that the in-distribution (ID) accuracy and OOD accuracy of models often show strong linear relationships. These relationships, called ‘accuracy-on-the-line’ (ACL) and ‘agreement-on-the-line’ (AGL), are useful for model selection and performance estimation. However, these relationships do not hold for all distribution shifts.
This paper investigates test-time adaptation (TTA) methods, which modify models to improve performance on OOD data. The key finding is that TTA not only improves OOD accuracy, but it also drastically strengthens the ACL and AGL trends, even in cases where those trends were previously weak. The authors show that TTA collapses the complexity of the distribution shifts, making them behave more like a simple scaling of the mean or covariance. This allows accurate OOD performance prediction and efficient hyperparameter selection for TTA without OOD labeled data.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between test-time adaptation (TTA) and the understanding of out-of-distribution (OOD) generalization. It provides a novel explanation for why TTA enhances OOD performance and offers practical strategies for hyperparameter tuning and model selection without OOD labels. This is highly relevant given the increasing focus on robust AI, especially in real-world applications where labeled OOD data is scarce.
Visual Insights#
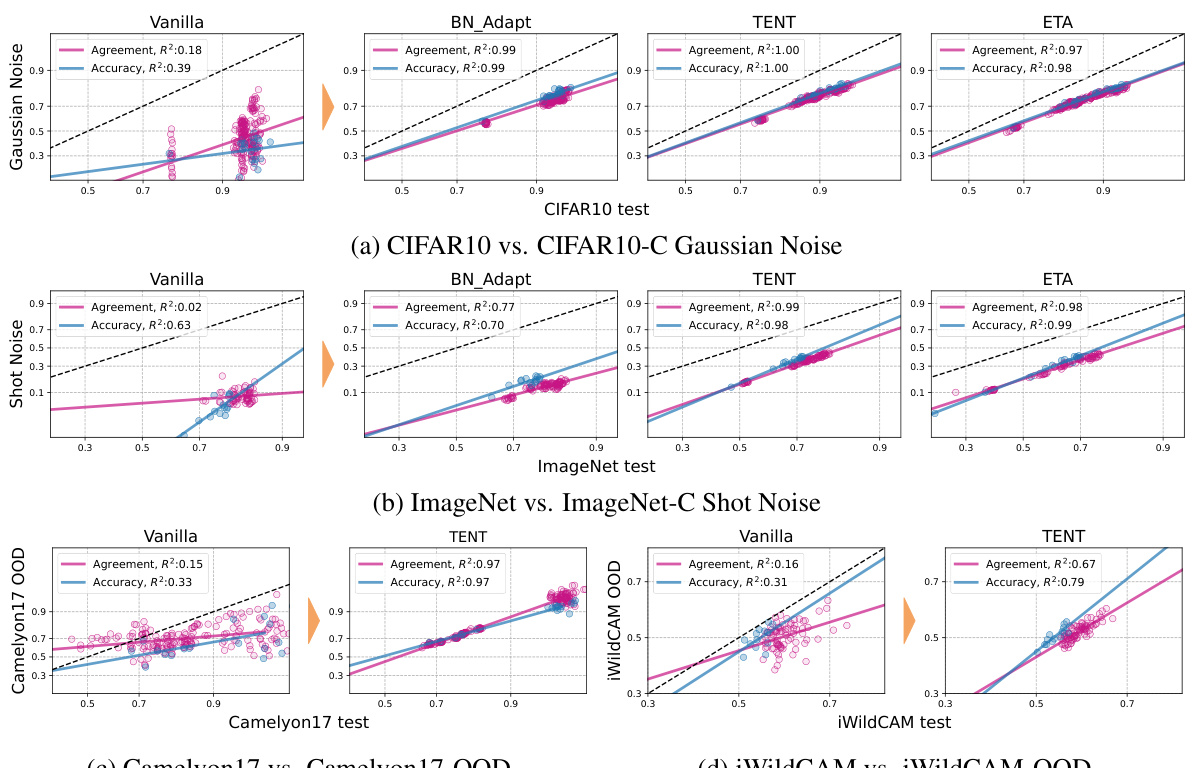
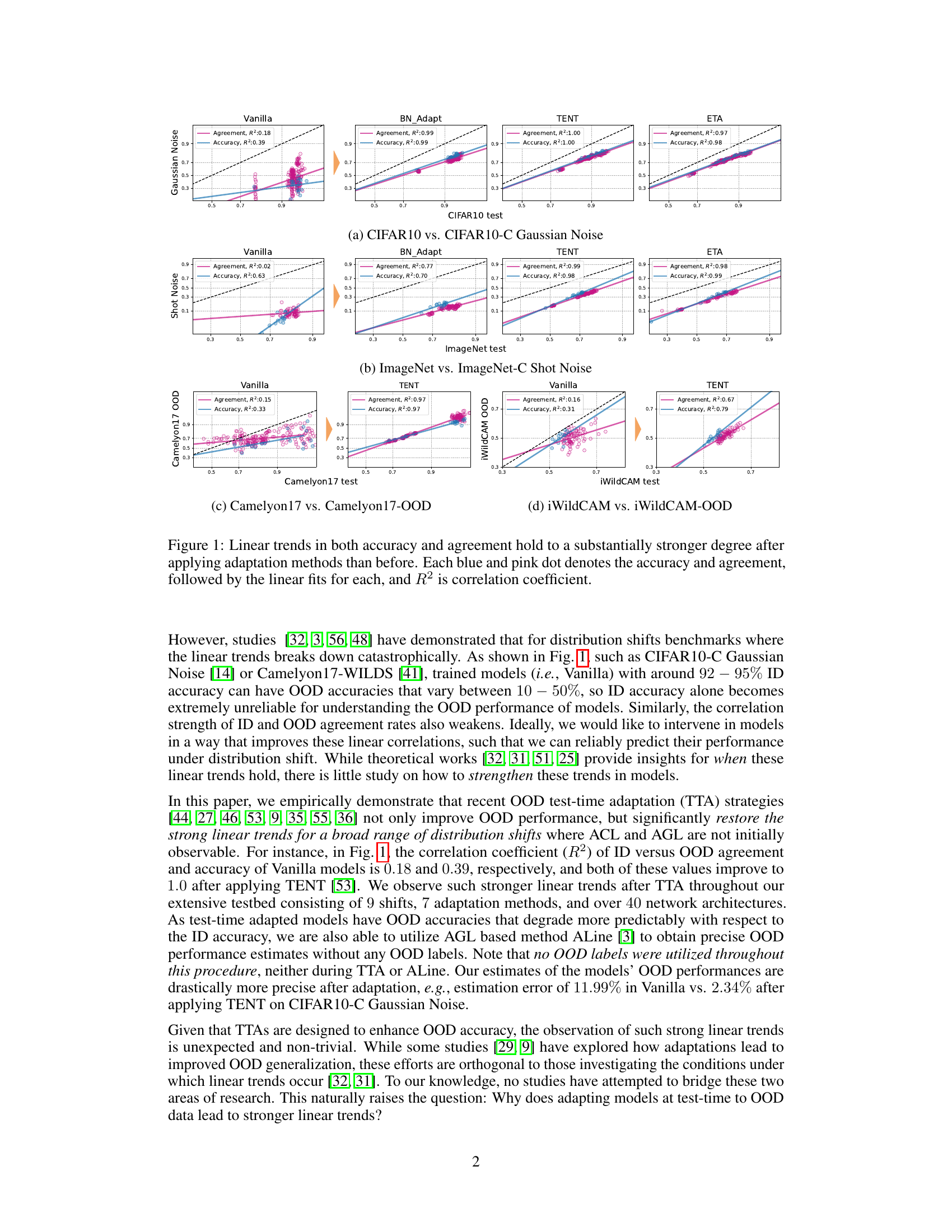
This figure shows the impact of test-time adaptation (TTA) on the linear relationship between in-distribution (ID) and out-of-distribution (OOD) accuracy and agreement. The plots compare the performance of vanilla models (without TTA) against models that have undergone TTA. Each point represents a single model, with its ID accuracy plotted against its OOD accuracy (or ID agreement against OOD agreement). The figure demonstrates that TTA significantly strengthens the linear correlation between ID and OOD performance, particularly for challenging distribution shifts where the correlation was weak in vanilla models. The R-squared (R²) values quantify the strength of these linear relationships.
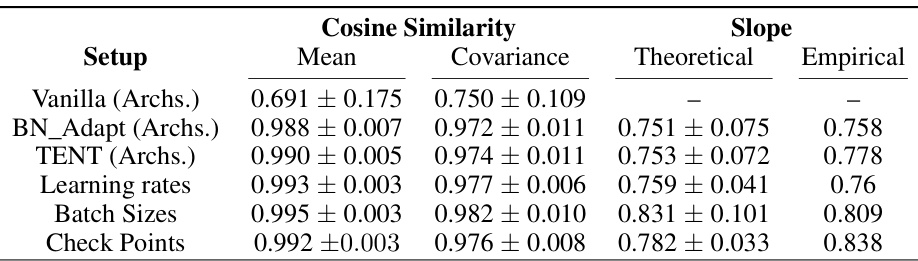
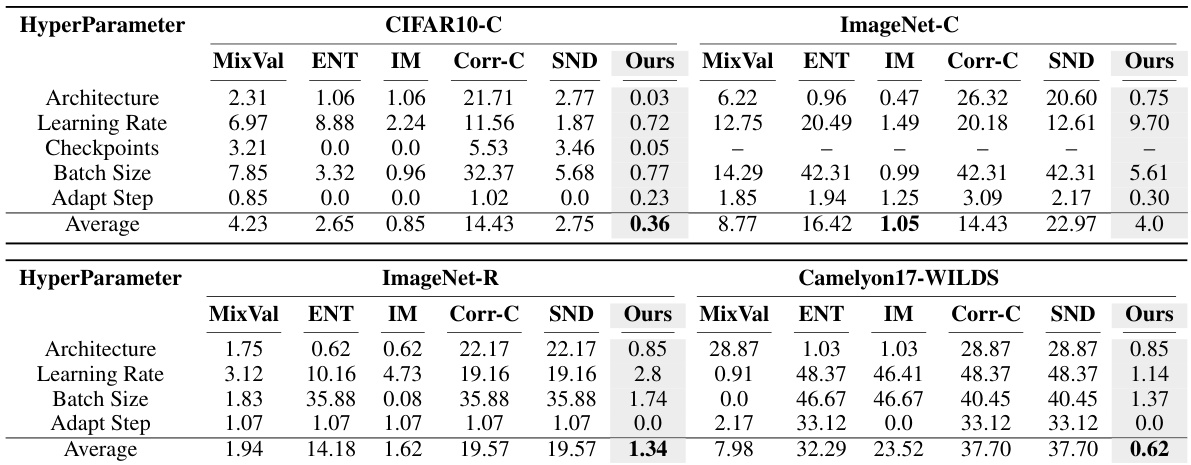
This table presents the results of an empirical analysis on the alignment of mean direction and covariance shape between the in-distribution (ID) and out-of-distribution (OOD) data after applying test-time adaptation (TTA) methods. It compares the cosine similarity of the normalized mean and covariance matrices of features extracted from the penultimate layer of models trained on CIFAR10 and tested on CIFAR10-C Gaussian Noise. The analysis is conducted across different network architectures and TTA hyperparameters, showing the impact of TTA on aligning the ID and OOD data distributions. The table also includes the theoretical and empirical slopes of the linear relationship between ID and OOD accuracy, allowing for a comparison between theoretical predictions and empirical results after TTA.
In-depth insights#
TTA & Linear Trends#
The paper explores the intriguing relationship between test-time adaptation (TTA) methods and the linear trends observed in in-distribution (ID) versus out-of-distribution (OOD) accuracy and agreement. A key finding is that TTA strengthens these linear correlations, even in cases where they were initially weak. This is significant because strong linear trends facilitate reliable OOD performance prediction and hyperparameter tuning without labeled OOD data. The authors investigate the theoretical underpinnings of this phenomenon by revisiting existing theoretical work, discovering that TTA methods effectively collapse complex distribution shifts into a simple scaling factor in the feature space. This simplification satisfies the theoretical conditions for strong linear trends, explaining why the correlations are enhanced after adaptation. This insight is valuable because it links the empirical success of TTA with a deeper theoretical understanding of distribution shifts, potentially guiding the development of future OOD generalization strategies.
AGL-based OOD est.#
The concept of ‘AGL-based OOD est.’ (Agreement-on-the-Line based Out-of-Distribution estimation) leverages the strong linear correlation observed between in-distribution (ID) and out-of-distribution (OOD) model agreement rates. This correlation, termed AGL, allows for precise OOD accuracy prediction without needing OOD labels. The method is particularly valuable when OOD labeled data is scarce. The effectiveness of AGL hinges on the linear relationship holding strongly. The paper explores how test-time adaptation (TTA) strengthens this linear trend, thereby enhancing the reliability and precision of AGL-based OOD estimation. TTA’s role is crucial, as it addresses situations where the initial AGL trend is weak or absent, substantially expanding the applicability of AGL-based methods. However, it’s important to note that the success relies on the conditions for AGL being met, such as distribution shifts affecting only mean and covariance scales in feature space. Further research could focus on understanding when and why AGL breaks down and developing more robust methods for situations where these conditions are not fully satisfied.
Theoretical Analysis#
A theoretical analysis section in a research paper about test-time adaptation (TTA) and its effects on accuracy and agreement on the line would ideally delve into the mathematical underpinnings of the observed phenomena. It would likely start by formalizing the assumptions made about the data distributions (e.g., Gaussianity), the model architecture (e.g., linearity), and the nature of the distribution shift (e.g., change in mean and variance). A key aspect would be deriving theoretical conditions under which strong linear correlations between in-distribution and out-of-distribution performance metrics are expected to emerge. This might involve proving theorems and lemmas about the relationships between model parameters, data statistics, and prediction accuracy/agreement. The analysis could then examine how TTA methods modify these relationships, potentially showing how they help satisfy the derived conditions for strong linearity. Furthermore, a solid theoretical analysis could explain why certain distribution shifts result in a breakdown of these linear trends and how TTA might mitigate such breakdowns. Crucially, the analysis would need to highlight the limitations and assumptions of the theoretical model, acknowledging that real-world data and deep neural networks are far more complex than the idealized scenarios often used in theoretical analyses. This would give context to the empirical results, providing a more comprehensive understanding of the strengths and weaknesses of the claims made in the paper.
Adaptation Strategies#
The effectiveness of various test-time adaptation (TTA) strategies in enhancing the accuracy and agreement-on-the-line (AGL) trends is a significant focus. The paper explores how these strategies, by modifying models at test time to better handle out-of-distribution (OOD) data, improve OOD generalization. A key finding is that TTA doesn’t just improve accuracy but also drastically strengthens the linear correlations between ID and OOD performance, even for challenging shifts where correlations were weak previously. This enhancement is explained by observing how TTA collapses the distribution shift’s complexity into a singular scaling variable in the feature space, satisfying theoretical conditions for strong linear trends. The study demonstrates the practical implications of stronger AGL trends by enabling precise OOD performance prediction and hyperparameter optimization for TTA without needing OOD labeled data. Combining TTA with AGL-based methods yields high-precision OOD performance estimation, offering valuable insights into the behavior of models under distribution shifts and providing practical tools for reliable deployment of neural networks.
Unsupervised Val.#
The heading ‘Unsupervised Val.’ likely refers to an experimental section on unsupervised model validation within the context of test-time adaptation (TTA) for neural networks. This is crucial because TTA methods often involve adapting model parameters to unseen data without labeled examples. The core challenge is assessing the effectiveness of different TTA strategies without using any out-of-distribution (OOD) labeled data. This section would likely detail a novel approach, or compare existing methods, for estimating OOD performance, potentially using metrics like agreement-on-the-line (AGL) and accuracy-on-the-line (ACL) which correlate in-distribution and OOD performance. The results would demonstrate the precision and reliability of this unsupervised validation technique, possibly comparing against other state-of-the-art methods. A key contribution may be showing how unsupervised validation guides hyperparameter selection for TTA, optimizing adaptation strategies without needing OOD labels, significantly reducing the reliance on scarce and costly OOD labeled data.
More visual insights#
More on figures

This figure shows the impact of test-time adaptation (TTA) methods on the linear correlation between in-distribution (ID) and out-of-distribution (OOD) accuracy and agreement. It compares vanilla models (without TTA) to models that have undergone TTA. The plots demonstrate that TTA significantly strengthens the linear relationships, even for distribution shifts where vanilla models exhibit weak correlations. The R² values quantify the strength of these correlations, highlighting the effectiveness of TTA in improving both accuracy and agreement on the line.

This figure visualizes the performance of different test-time adaptation (TTA) methods in estimating out-of-distribution (OOD) accuracy. The x-axis represents the ground truth OOD accuracy, while the y-axis shows the OOD accuracy estimated using a hyperparameter selection method. Each point represents a model with specific hyperparameters. The plot helps assess the effectiveness of each TTA method in predicting OOD accuracy and how well the hyperparameter selection performs. The cross markers show the best OOD model selected by the hyperparameter selection method, while the circle markers show the average across hyperparameters. This allows a comparison of the best-performing hyperparameters and the overall average behavior of each TTA method.
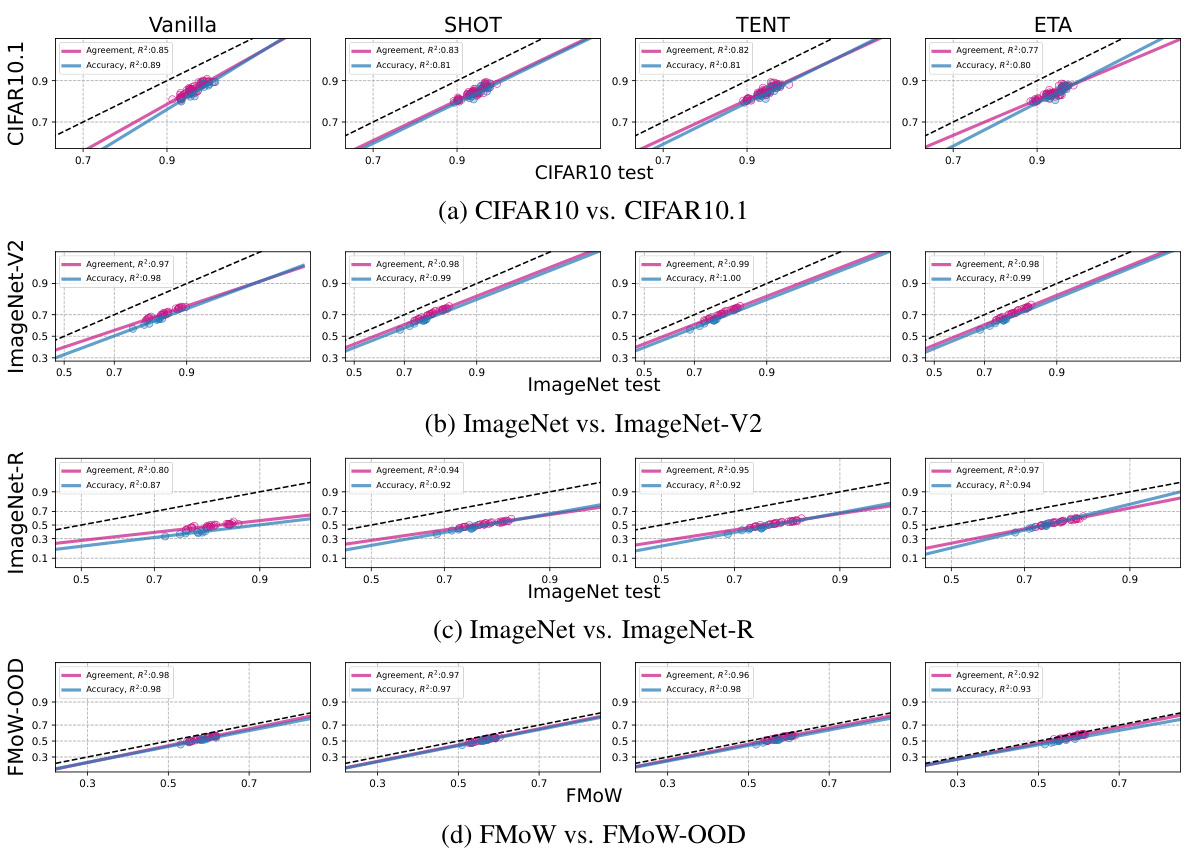
This figure displays the accuracy and agreement of vanilla models and models with test-time adaptation (TTA) methods on various out-of-distribution (OOD) datasets. Each subfigure shows a different OOD dataset. The x-axis represents the in-distribution (ID) accuracy, and the y-axis represents the OOD accuracy and agreement. The blue dots represent the accuracy, and the pink dots represent the agreement. The solid lines show the linear fit for accuracy and agreement, and the R² value indicates the strength of the linear correlation. The figure demonstrates that TTA methods not only improve OOD performance, but also significantly strengthen the linear correlations between ID and OOD accuracy and agreement.
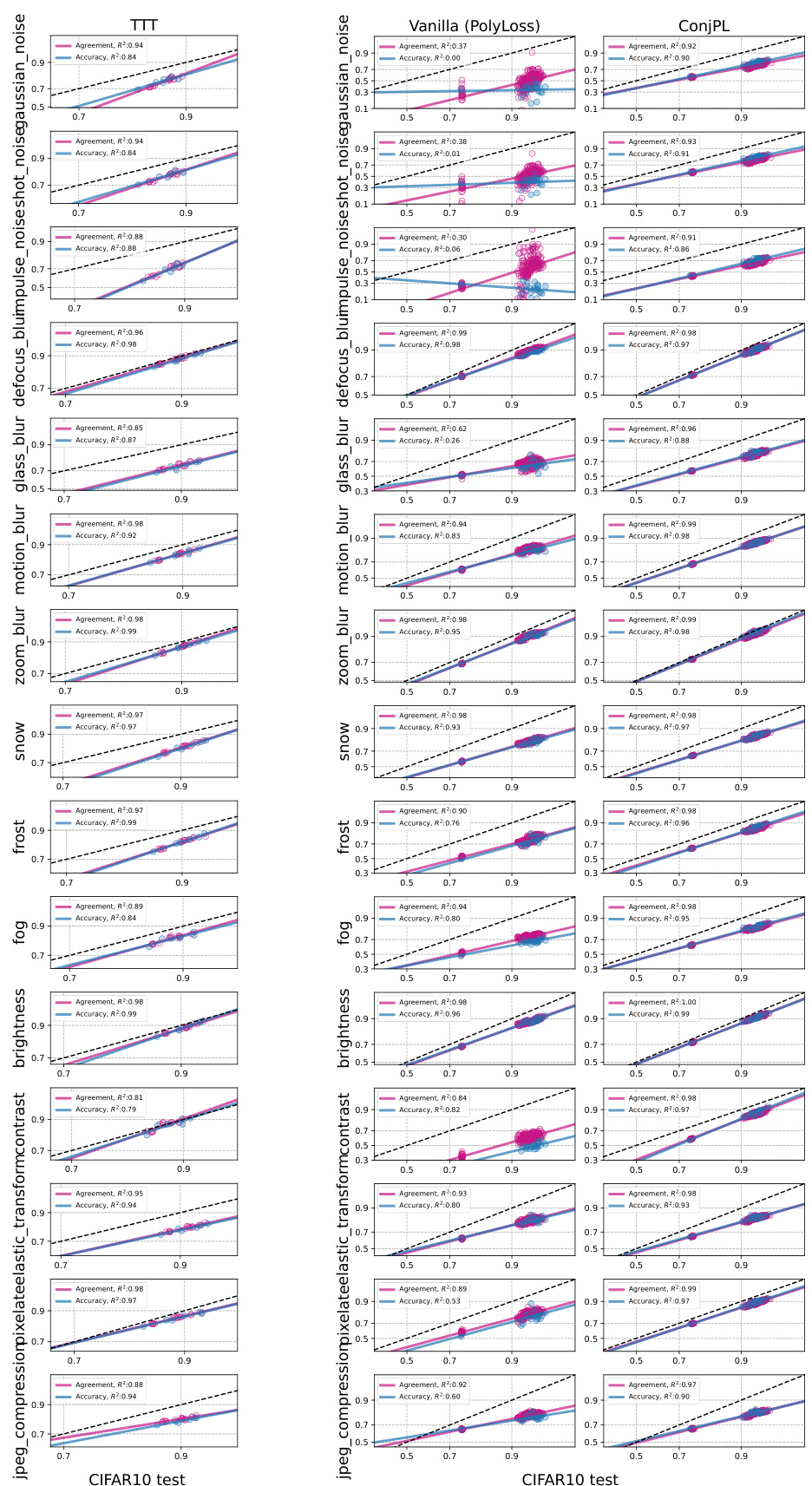
This figure visualizes the impact of test-time adaptation (TTA) on the linear correlation between in-distribution (ID) and out-of-distribution (OOD) accuracy and agreement. It shows that before adaptation (Vanilla), some distribution shifts exhibit weak correlations. After applying TTA methods like BN Adapt and TENT, the linear trends become considerably stronger. This demonstrates TTA’s effectiveness in improving not only OOD performance but also the reliability of using ID accuracy and agreement for OOD prediction.
This figure shows the accuracy and agreement-on-the-line (AGL) trends for several test-time adaptation methods and Vanilla models on four different datasets. It demonstrates that test-time adaptation improves the strength of the linear correlation between in-distribution (ID) and out-of-distribution (OOD) accuracy and agreement, even in cases where Vanilla models show weak correlations. Each subplot represents a different dataset and shows the accuracy and agreement rates for various models. The R-squared values quantify the strength of the linear fits.
This figure shows the impact of test-time adaptation (TTA) on the linear relationship between in-distribution (ID) and out-of-distribution (OOD) accuracy and agreement. It compares the performance of vanilla models (without TTA) to models that have undergone adaptation using various TTA methods. The plots demonstrate that TTA significantly strengthens the linear trends, improving the correlation (R²) between ID and OOD performance. This is particularly evident in cases where vanilla models exhibited weak correlations. The figure visually represents this improvement by showing tighter clusters of data points around the linear fits, indicating higher correlation and predictability in OOD performance based on ID accuracy and agreement.

This figure shows the improvement in the strength of linear correlations between in-distribution (ID) and out-of-distribution (OOD) accuracy and agreement after applying test-time adaptation (TTA) methods. Each subplot represents a different distribution shift benchmark. The blue dots represent the agreement, and pink dots represent accuracy. The lines are the linear fits, and R² is the coefficient of determination representing the goodness of fit. It demonstrates that TTA strengthens the ‘accuracy-on-the-line’ (ACL) and ‘agreement-on-the-line’ (AGL) trends, enabling more precise OOD performance estimation.
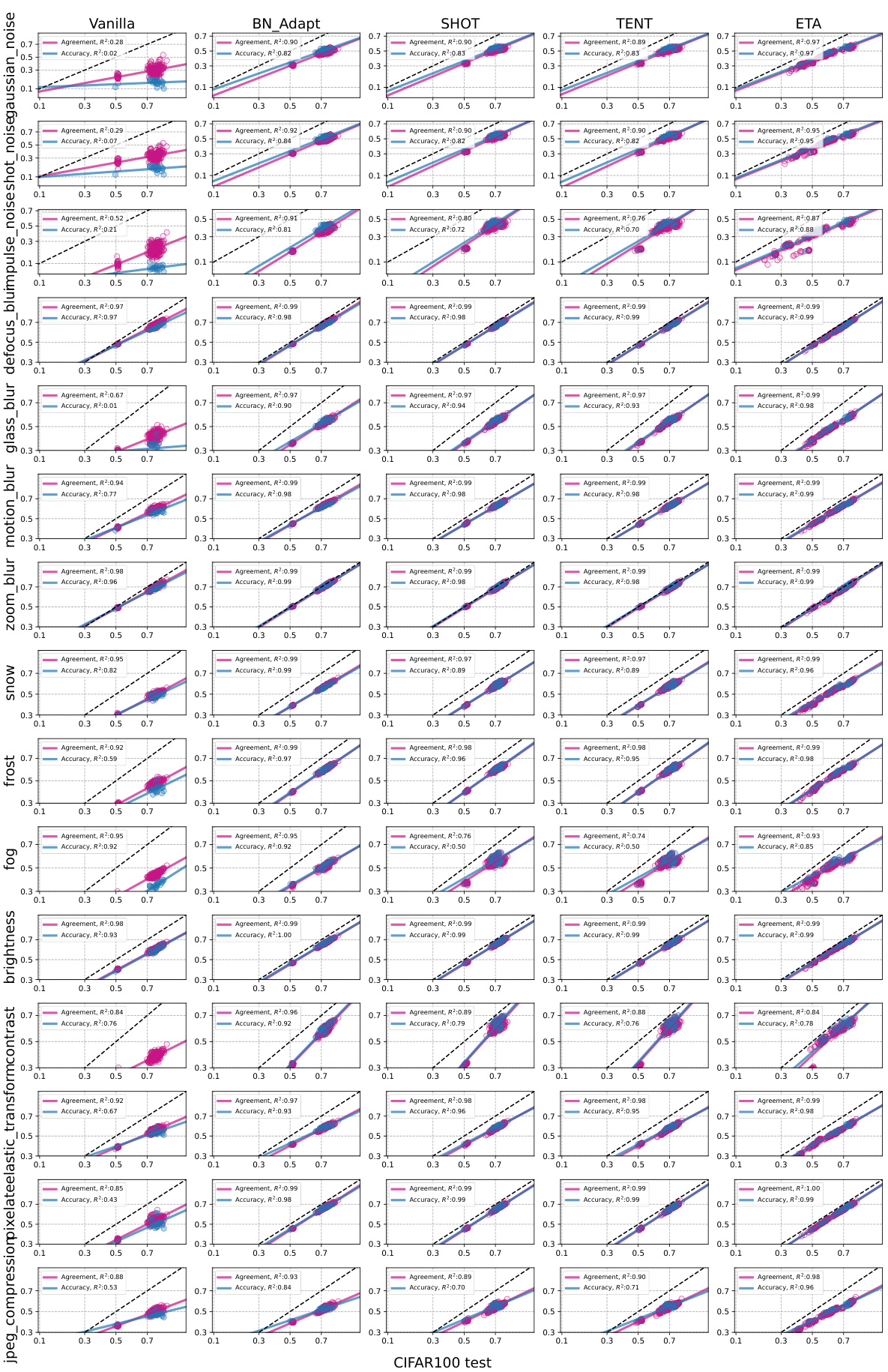
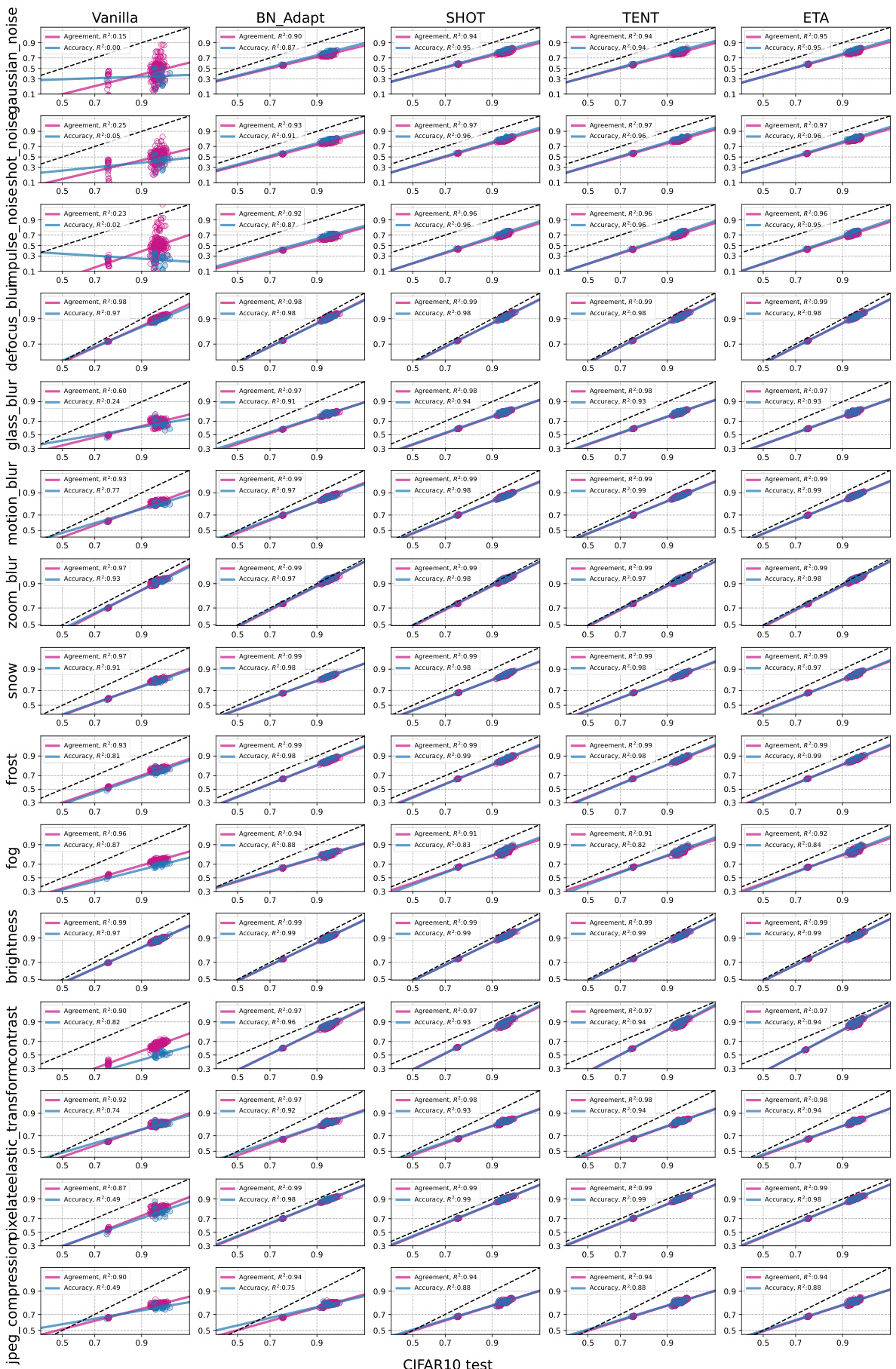
This figure displays the results of applying various test-time adaptation (TTA) methods on CIFAR10-C corruptions. It shows the relationship between In-distribution (ID) accuracy and Out-of-distribution (OOD) accuracy, as well as the agreement between model pairs. Each plot represents a specific type of corruption applied to CIFAR10. The plots compare the performance of the vanilla model (without adaptation) to the performance after adapting using BN_Adapt, SHOT, TENT, and ETA methods. The R-squared values (R²) are displayed indicating the strength of the linear correlation in accuracy and agreement for each method and corruption type. The plots highlight that the TTA methods generally induce much stronger linear correlations (higher R²) compared to the vanilla model, suggesting stronger agreement-on-the-line (AGL) and accuracy-on-the-line (ACL) trends after adaptation.

This figure displays the accuracy and agreement-on-the-line (AGL) results for various distribution shifts before and after test-time adaptation (TTA). Each point represents a model’s ID (in-distribution) and OOD (out-of-distribution) accuracy and agreement. The lines show linear fits, and R-squared values indicate the strength of the correlation. The figure demonstrates that TTA significantly improves the strength of the linear correlation between ID and OOD performance, even for shifts where correlations were initially weak.
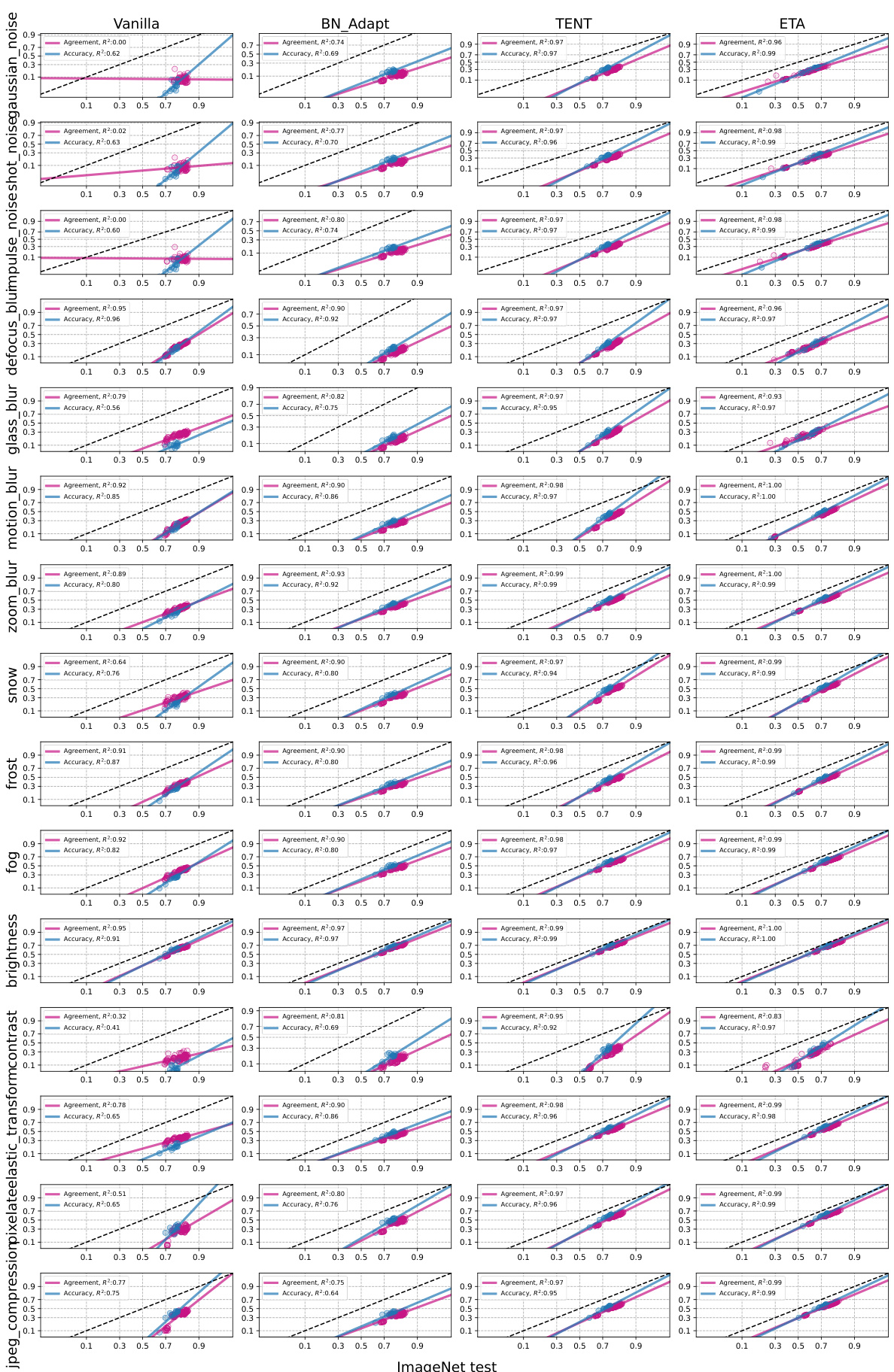
This figure shows the impact of test-time adaptation (TTA) methods on the linear correlation between in-distribution (ID) and out-of-distribution (OOD) accuracy and agreement. It compares the performance of vanilla models (no adaptation) to models using various TTA techniques across different distribution shifts. The plots demonstrate that TTA consistently strengthens the linear trends, indicating a more predictable relationship between ID and OOD performance.
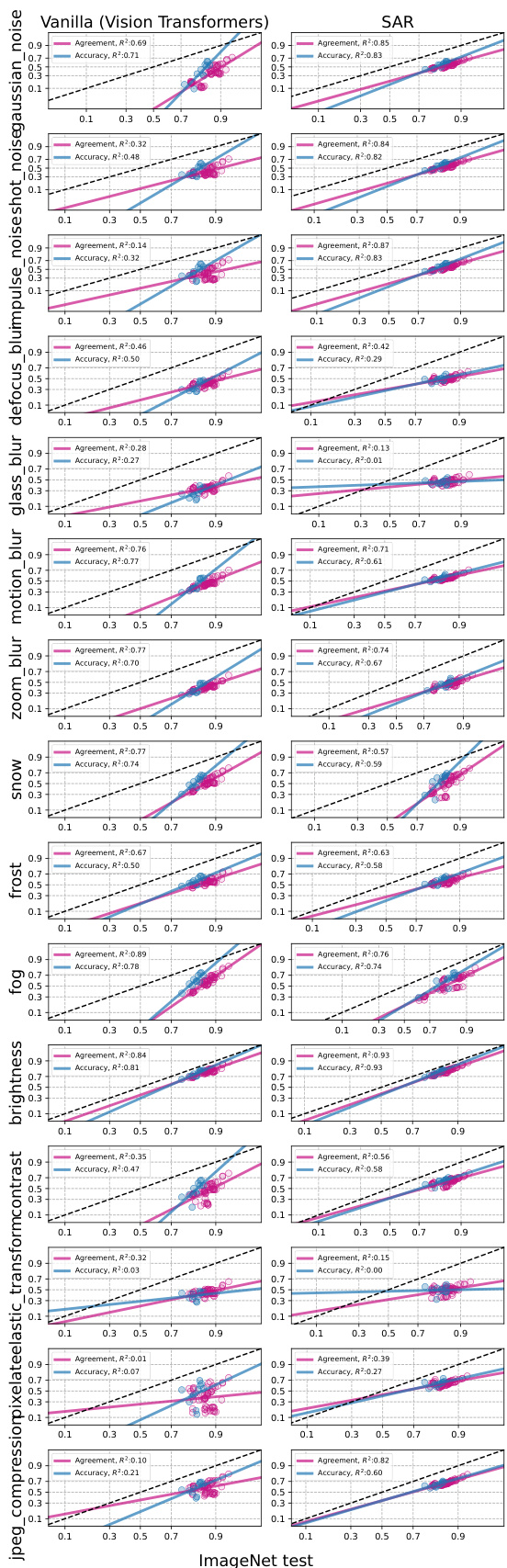
This figure shows the accuracy and agreement-on-the-line (AGL) for various models before and after test-time adaptation (TTA) across different distribution shifts. Each point represents a model’s in-distribution (ID) accuracy versus out-of-distribution (OOD) accuracy and agreement, and the lines show the linear fits. It demonstrates that TTA strengthens the linear correlations between ID and OOD performance metrics.
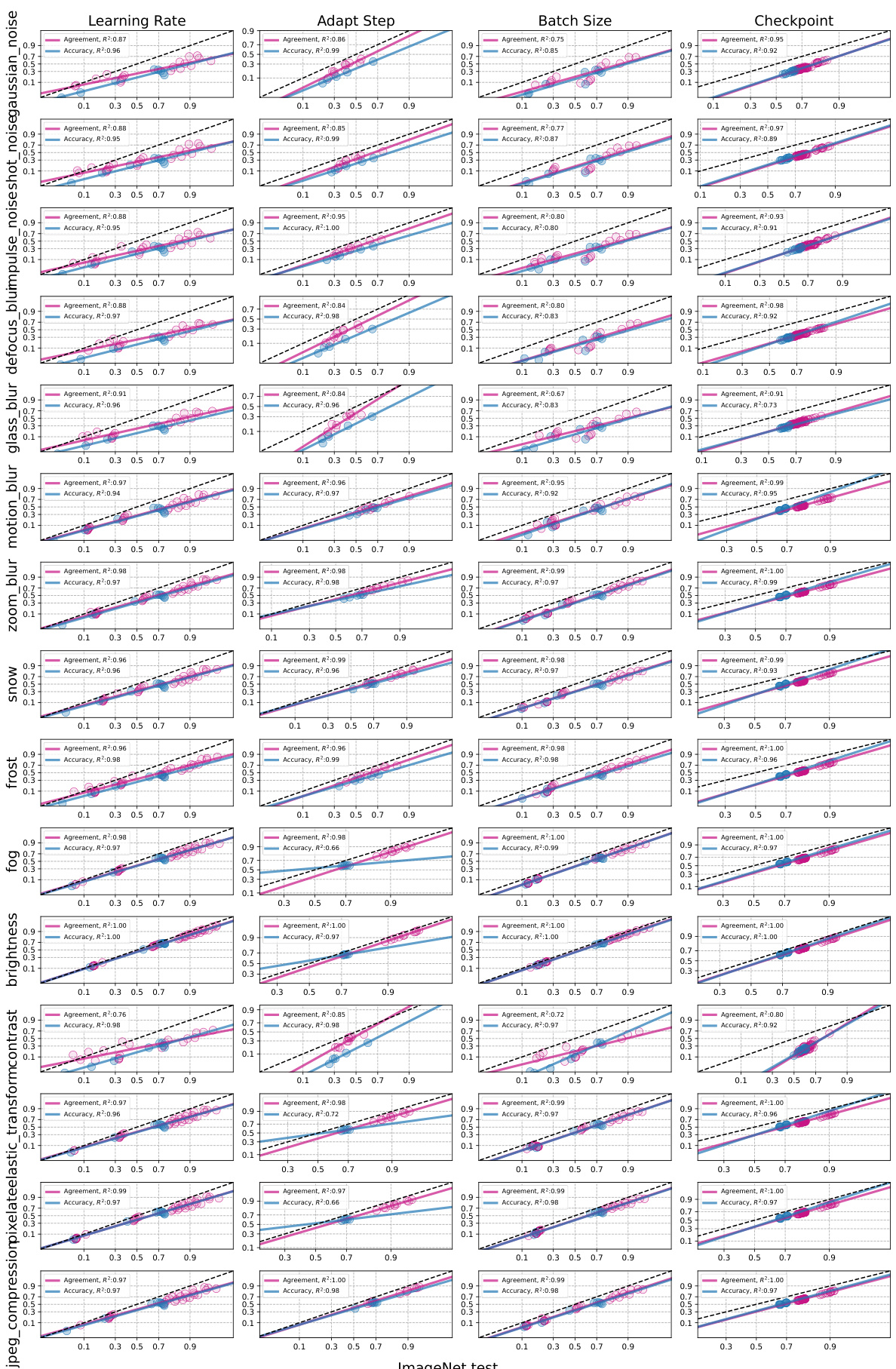
This figure shows the accuracy and agreement on the line (AGL) before and after applying test-time adaptation (TTA) methods for several different distribution shifts. Each point represents a model’s in-distribution (ID) and out-of-distribution (OOD) accuracy and agreement. The lines show the linear regression fits for each metric. A stronger linear correlation is observed after applying TTA, especially in shifts where the initial correlations were weak.
More on tables
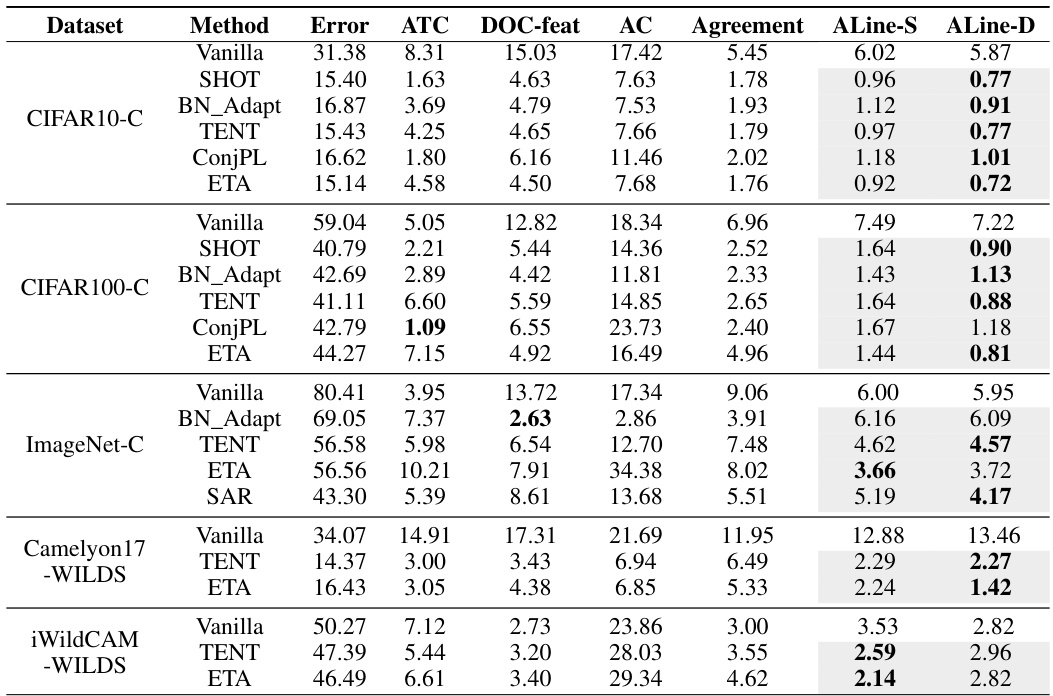
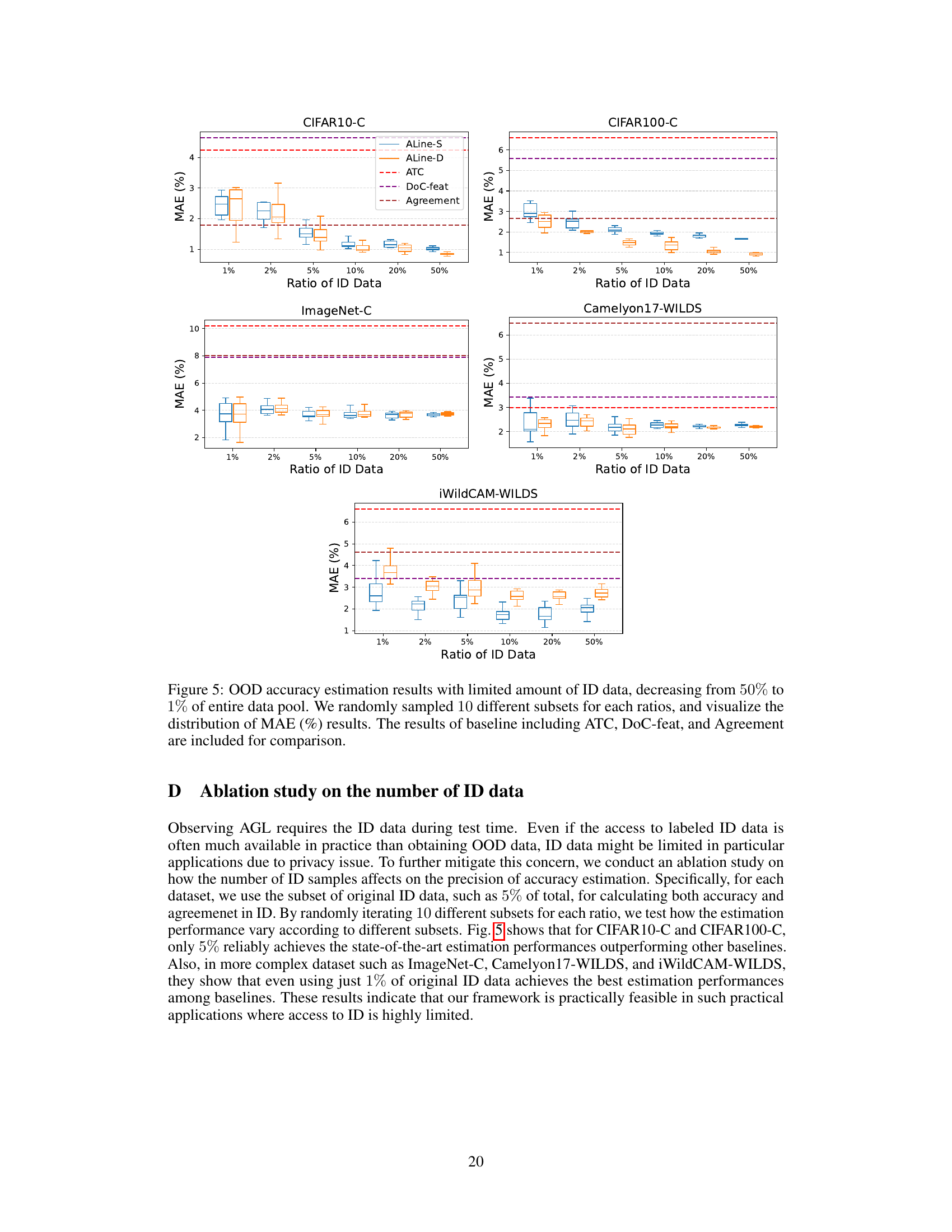
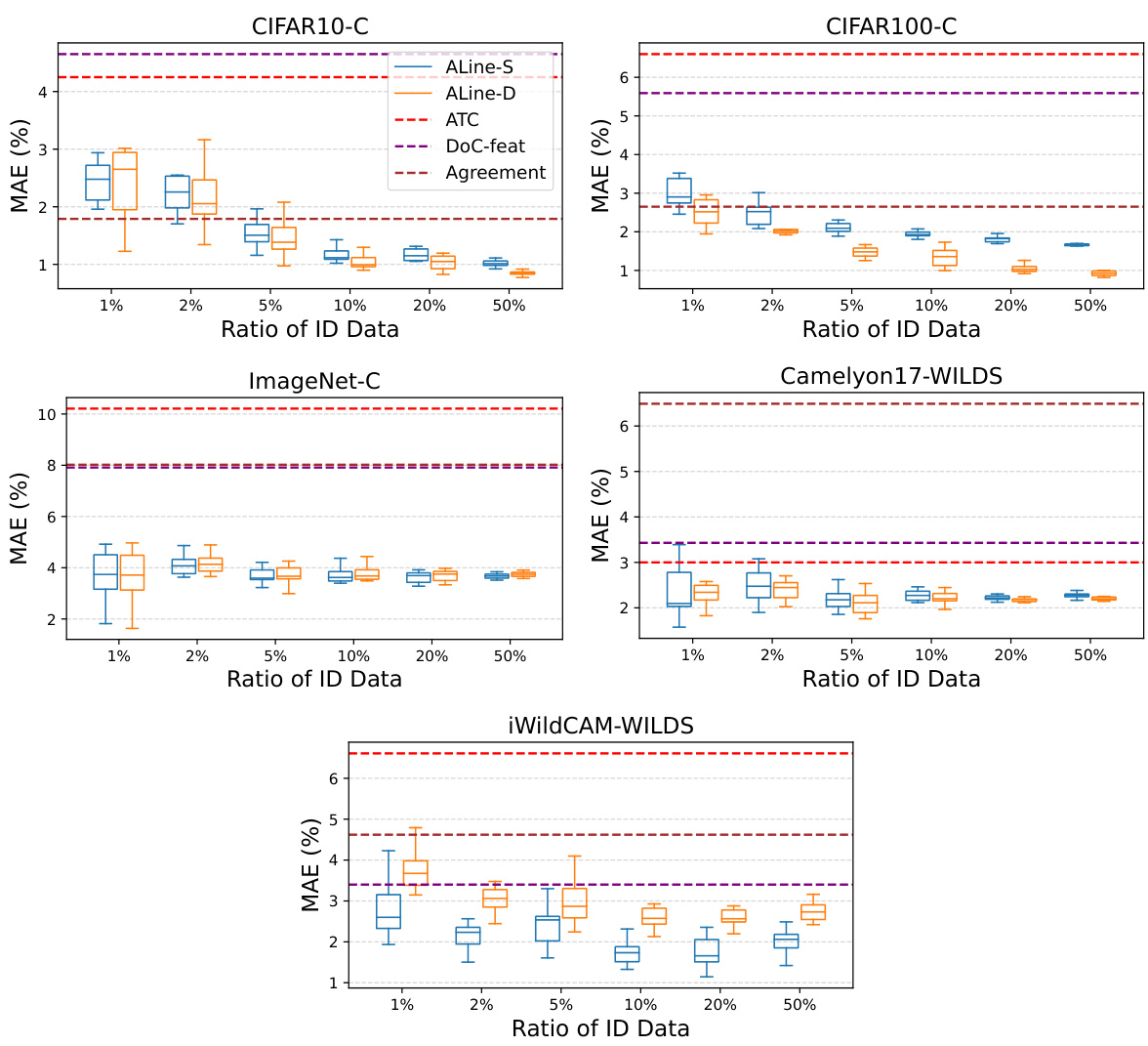
This table presents the mean absolute error (MAE) of out-of-distribution (OOD) accuracy estimation using different methods. It compares the accuracy estimations from different methods (ALine-S, ALine-D, ATC, DOC-feat, Agreement) before and after test-time adaptation (TTA) on various datasets (CIFAR10-C, CIFAR100-C, ImageNet-C, Camelyon17-WILDS, iWildCAM-WILDS). Bold values highlight the methods with the lowest MAE for each dataset. Gray shading indicates results obtained after TTA. The classification error for each method, before and after adaptation, is also provided.
This table presents the cosine similarity of mean direction and covariance shape between CIFAR10 and CIFAR10-C Gaussian Noise features, computed using the penultimate layer of various model architectures and TTA hyperparameters. It compares the theoretical and empirical slopes of the linear trend between ID and OOD accuracy. The results demonstrate that Test-Time Adaptation (TTA) methods align the mean and covariance, closely matching the theoretical conditions for linear trends.
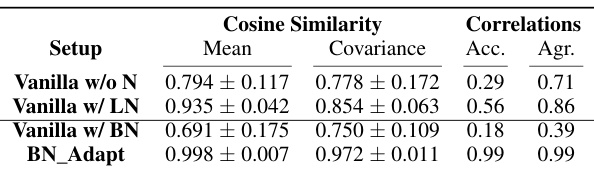
This table presents the cosine similarity of mean direction and covariance shape between CIFAR10 and CIFAR10-C Gaussian Noise features extracted from the penultimate layer of various models. It compares these empirical results with theoretically predicted slopes under the Gaussian assumption in Miller et al. [32]. The results are shown for different model architectures and hyperparameters, highlighting the impact of test-time adaptation (TTA) on the alignment of feature distributions.

This table presents the cosine similarity of mean direction and covariance shape between CIFAR10 and CIFAR10-C Gaussian Noise features, extracted from the penultimate layer of various model architectures, both before and after test-time adaptation (TTA). It compares the empirical slope of the resulting linear trend in accuracy to the theoretical slope predicted by the Gaussian data setup described in the paper. The results highlight how TTA aligns the mean and covariance, bringing the empirical closer to theoretical results, and demonstrating the effect of TTA on the linear trend.

This table presents the results of an empirical analysis conducted to investigate the alignment of mean and covariance between in-distribution (ID) and out-of-distribution (OOD) data in the feature space of deep neural networks. The cosine similarity of normalized means and covariances are measured, representing the alignment. The comparison between theoretical and empirical slope for the linear trend between ID and OOD accuracy further validates these findings. Results are shown for different network architectures and hyperparameter settings applied to CIFAR10 vs. CIFAR10-C Gaussian Noise dataset.

This table presents the cosine similarity of mean direction and covariance shape between the features of CIFAR10 and CIFAR10-C Gaussian noise data, calculated at the penultimate layer of different neural network architectures. It compares the results before and after applying test-time adaptation (TTA) methods, demonstrating how TTA aligns the mean and covariance of ID and OOD data, leading to stronger linear trends. The table also shows the theoretical and empirical slopes, highlighting the strong match between them after adaptation.

This table shows the cosine similarity of mean direction and covariance shape of the penultimate layer features for CIFAR10 and CIFAR10-C Gaussian noise, before and after applying test-time adaptation methods. It also compares the theoretical and empirical slopes of the linear relationship between in-distribution (ID) and out-of-distribution (OOD) accuracy. The results are shown for different network architectures and various hyperparameters used in the test-time adaptation methods.
Full paper#