↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world applications demand highly interpretable machine learning models, but existing rule learning methods struggle to balance simplicity, accuracy, and scalability. Deep learning, while powerful, often lacks transparency, hindering its use in critical domains requiring explainable decision-making processes.
HyperLogic tackles this challenge by integrating hypernetworks with rule-learning networks. Hypernetworks generate diverse sets of weights for the main network, boosting flexibility. The paper shows theoretically that this approach reduces approximation errors and improves generalization. Experiments on various datasets demonstrate the effectiveness of HyperLogic in learning accurate and concise rules, exceeding the performance of several existing rule learning models.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel and flexible approach to enhance the interpretability and accuracy of rule learning models. It bridges the gap between the high performance of deep learning and the need for transparent decision-making, particularly relevant in high-stakes domains like healthcare and finance. The theoretical analysis and empirical results demonstrate significant advancements in the field, paving the way for improved trustworthiness and wider applicability of machine learning models.
Visual Insights#

The figure illustrates the HyperLogic framework, which uses a hypernetwork to generate weights for a main rule-learning network. The hypernetwork takes random samples from a distribution as input and outputs weights for different parts of the main network. The main network, in this case, a simple two-layer rule-learning network, learns if-then rules from the generated weights. The rules are extracted from the learned weights in the rule-learning network. The process involves two loss functions: one for the hypernetwork and one for the task (rule learning). The combined loss is used to train the whole system and extract meaningful if-then rules from the data.
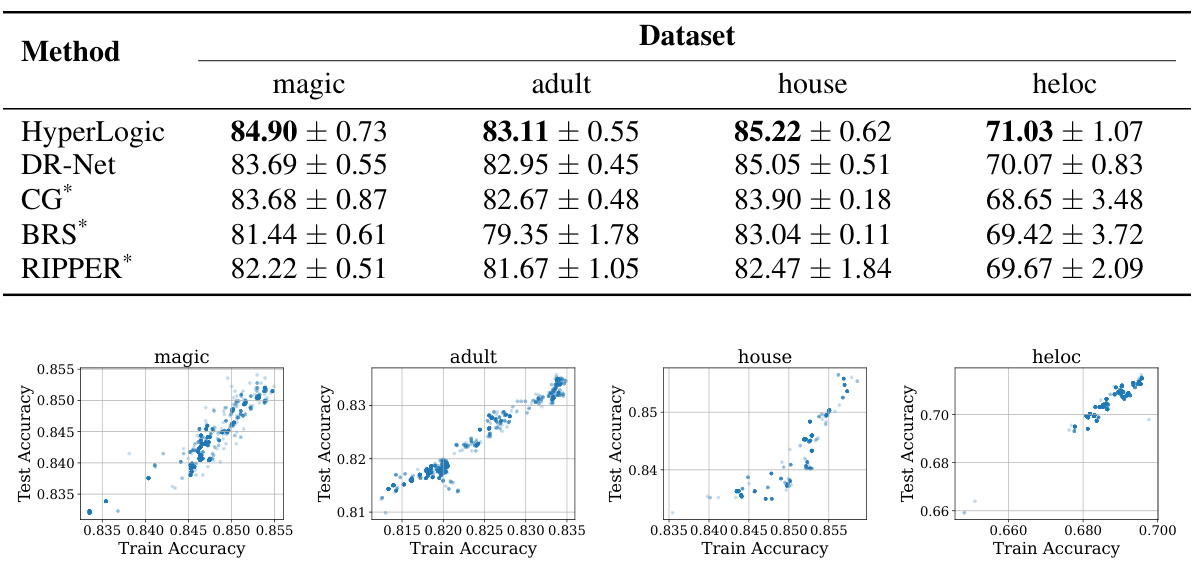
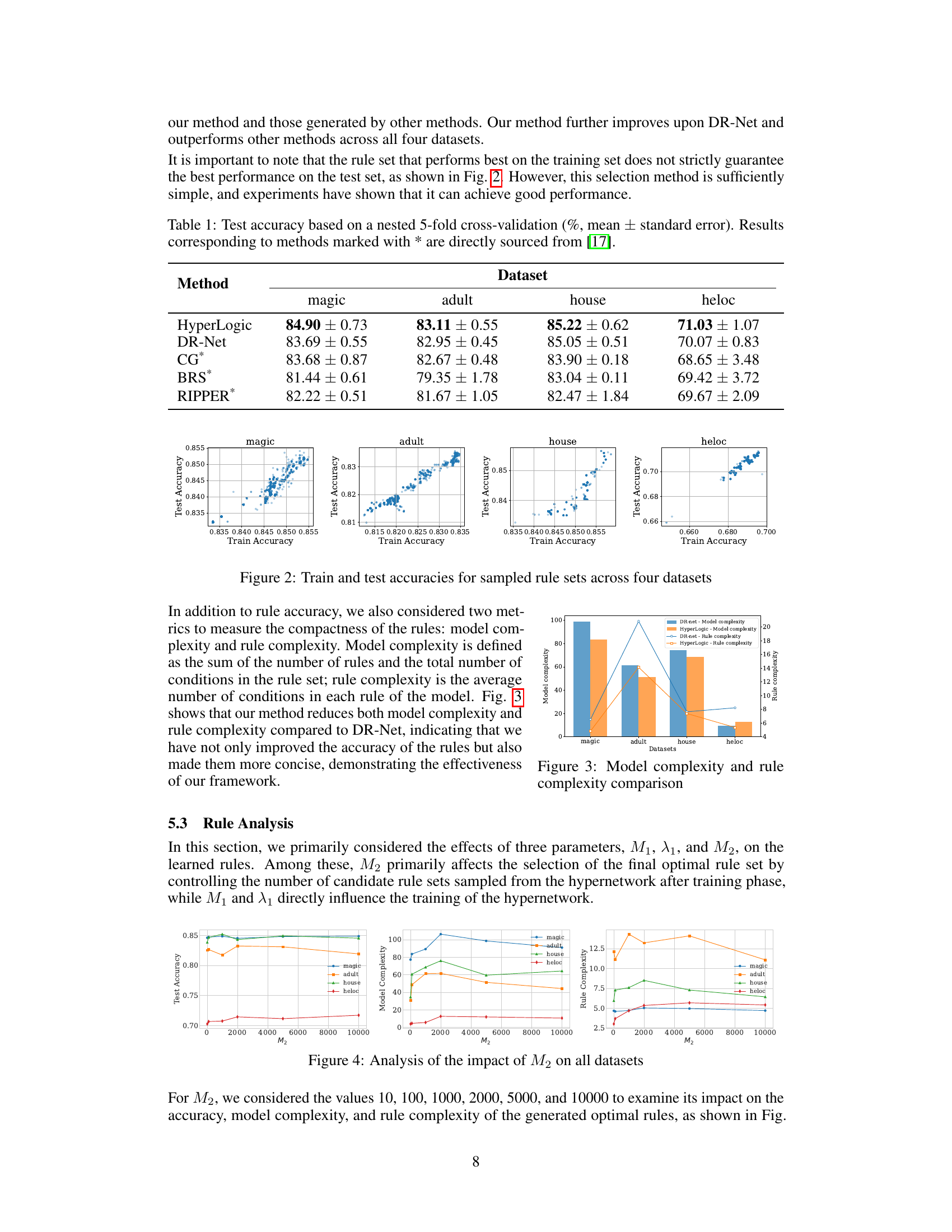
This table presents the test accuracy results of the HyperLogic model and other baseline models across four datasets (magic, adult, house, heloc). The accuracy is calculated using nested 5-fold cross-validation, and the results are reported as mean ± standard error. The baseline models include DR-Net, CG, BRS, and RIPPER. Results for the latter three models are taken from the cited reference [17].
In-depth insights#
HyperLogic’s Core#
HyperLogic’s core centers around using hypernetworks to enhance the flexibility and accuracy of differentiable rule learning. It cleverly addresses the limitations of traditional approaches by generating diverse rule sets, rather than relying on a single, potentially restrictive, model. This method enhances model interpretability without sacrificing accuracy by allowing the extraction of concise and accurate if-then rules from the learned network weights. The integration of hypernetworks also introduces scalability, enabling the efficient handling of complex, high-dimensional datasets. Theoretical analysis further supports HyperLogic’s effectiveness, demonstrating its ability to act as a universal approximation estimator and achieve generalization under various regularization schemes. The framework is versatile and adaptable, capable of integration with various main rule-learning networks, thus offering a flexible solution for a variety of tasks.
Rule Diversity Effects#
Rule diversity, in the context of rule learning models, refers to the variety and heterogeneity of rules generated by a system. High rule diversity is often associated with improved model accuracy and robustness, as diverse rules capture different aspects and patterns within the data. However, excessively diverse rule sets can lead to decreased interpretability and may overfit the training data, reducing generalization performance. A key challenge is finding the optimal balance between diversity and other desirable properties, such as accuracy, conciseness, and interpretability. Methods for promoting rule diversity might include incorporating regularization techniques, using hypernetworks to generate diverse rule sets, or employing ensemble methods that combine multiple rule sets. Understanding the interplay between rule diversity, accuracy, and interpretability is crucial for building effective and trustworthy rule-based machine learning models. The practical implications of rule diversity involve choosing appropriate evaluation metrics that consider not only accuracy but also the nature and complexity of the rule set. Ultimately, the goal is to develop techniques that enable the creation of rule sets that are both highly accurate and easily understandable by humans.
Hypernetwork’s Role#
The hypernetwork plays a crucial role in HyperLogic by generating the weights for the main rule-learning network. This approach offers several key advantages. First, it enhances model flexibility, enabling HyperLogic to capture complex data patterns that simpler, interpretable models might miss. Second, it addresses the common challenge of balancing interpretability and model complexity in rule learning. By generating diverse rule sets, each potentially capturing different patterns, HyperLogic avoids the limitations of simplistic rule structures, while retaining the crucial element of interpretability. Third, the hypernetwork allows the generation of multiple rule sets in a single training session, improving efficiency without compromising interpretability. This flexibility is a key advantage over traditional rule learning methods that typically learn only one rule set at a time. Finally, the theoretical analysis of the hypernetwork’s role demonstrates its effectiveness in approximation and generalization, providing a strong foundation for the method’s performance.
Ensemble Learning#
The section on ensemble learning explores leveraging the diversity of rule sets generated by the HyperLogic framework. Instead of relying on a single optimal rule set, ensemble learning combines multiple rule sets to improve overall model performance. The authors utilize a simple averaging voting method, selecting top-performing rule sets based on training accuracy and evaluating them on test data. Results show an initial increase in test accuracy with increasing ensemble size, but further increases in ensemble size lead to a slight decline, indicating an optimal ensemble size exists. This suggests a balance is needed between diversity and accuracy; too much diversity may introduce noise and reduce performance. Future research could explore more sophisticated ensemble techniques beyond simple averaging to further enhance accuracy and address limitations in diversity management.
Future Directions#
Future research could explore several promising avenues. Extending HyperLogic to handle non-binary data would significantly broaden its applicability, moving beyond simple binary features to accommodate diverse data types. Investigating alternative hypernetwork architectures and weight generation methods could improve efficiency and stability, potentially leading to more accurate and diverse rule sets. Developing more sophisticated regularization techniques to control the complexity of generated rules is another critical area. Finally, a thorough comparative analysis against other rule learning methods on a wider range of benchmark datasets would solidify HyperLogic’s position and identify its strengths and weaknesses more precisely. These improvements would enhance HyperLogic’s practical utility and theoretical understanding, making it a more robust and valuable tool in the field of interpretable machine learning.
More visual insights#
More on figures
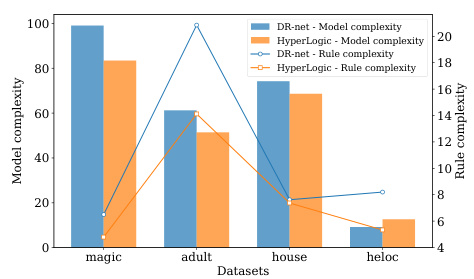
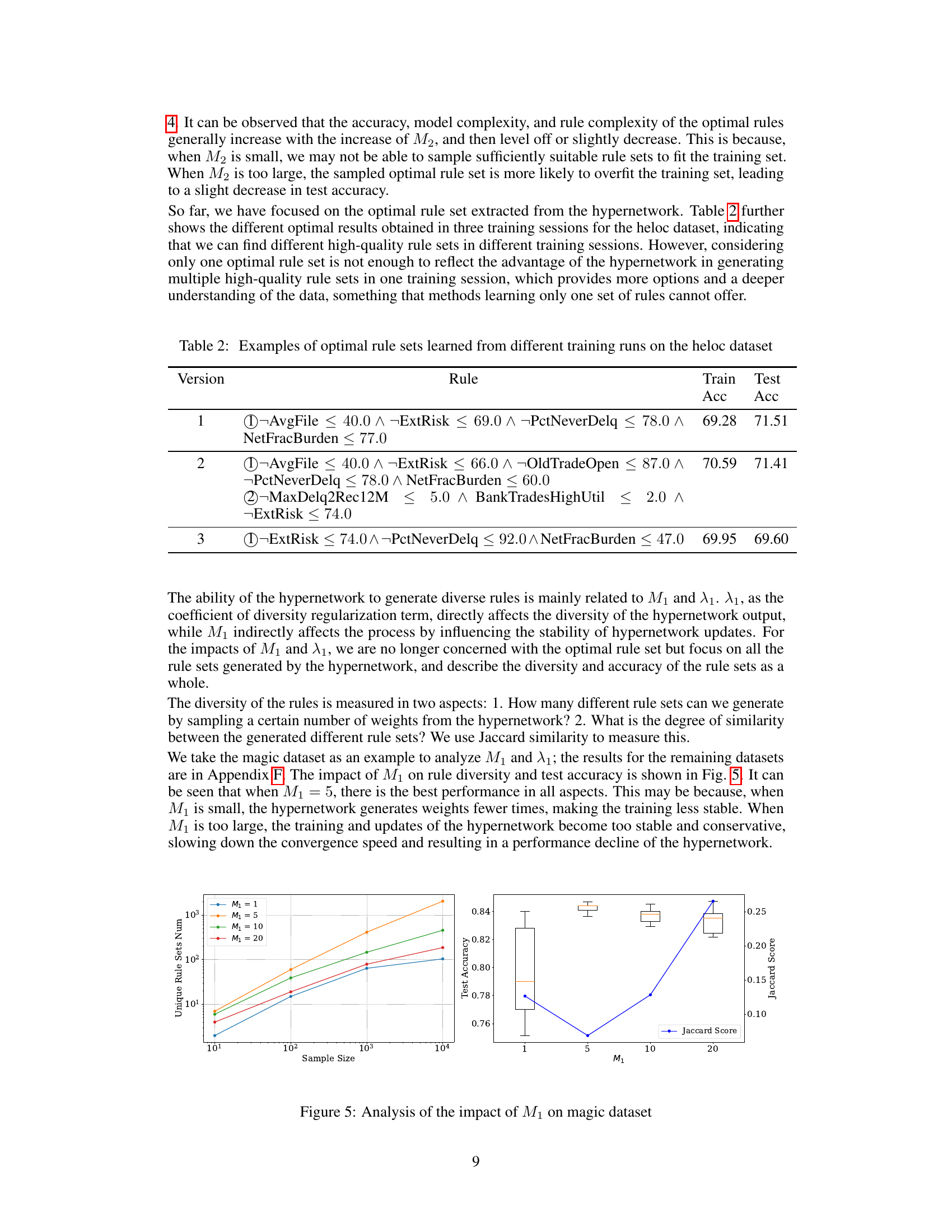
This figure compares the model complexity and rule complexity of HyperLogic and DR-Net across four datasets: magic, adult, house, and heloc. Model complexity represents the sum of the number of rules and the total number of conditions in the rule set, while rule complexity is the average number of conditions in each rule. The results show that HyperLogic achieves a lower model complexity and rule complexity compared to DR-Net across all four datasets.

This figure analyzes the effect of the hyperparameter M2 (number of rule sets sampled for selecting the optimal rule set) on the performance of HyperLogic across four datasets: magic, adult, house, and heloc. The left panel shows the test accuracy, the middle panel depicts model complexity (sum of rules and conditions), and the right panel displays average rule complexity (conditions per rule). The plots reveal the trend of performance metrics across different values of M2. For instance, it shows the point where model complexity and rule complexity are balanced with accuracy.

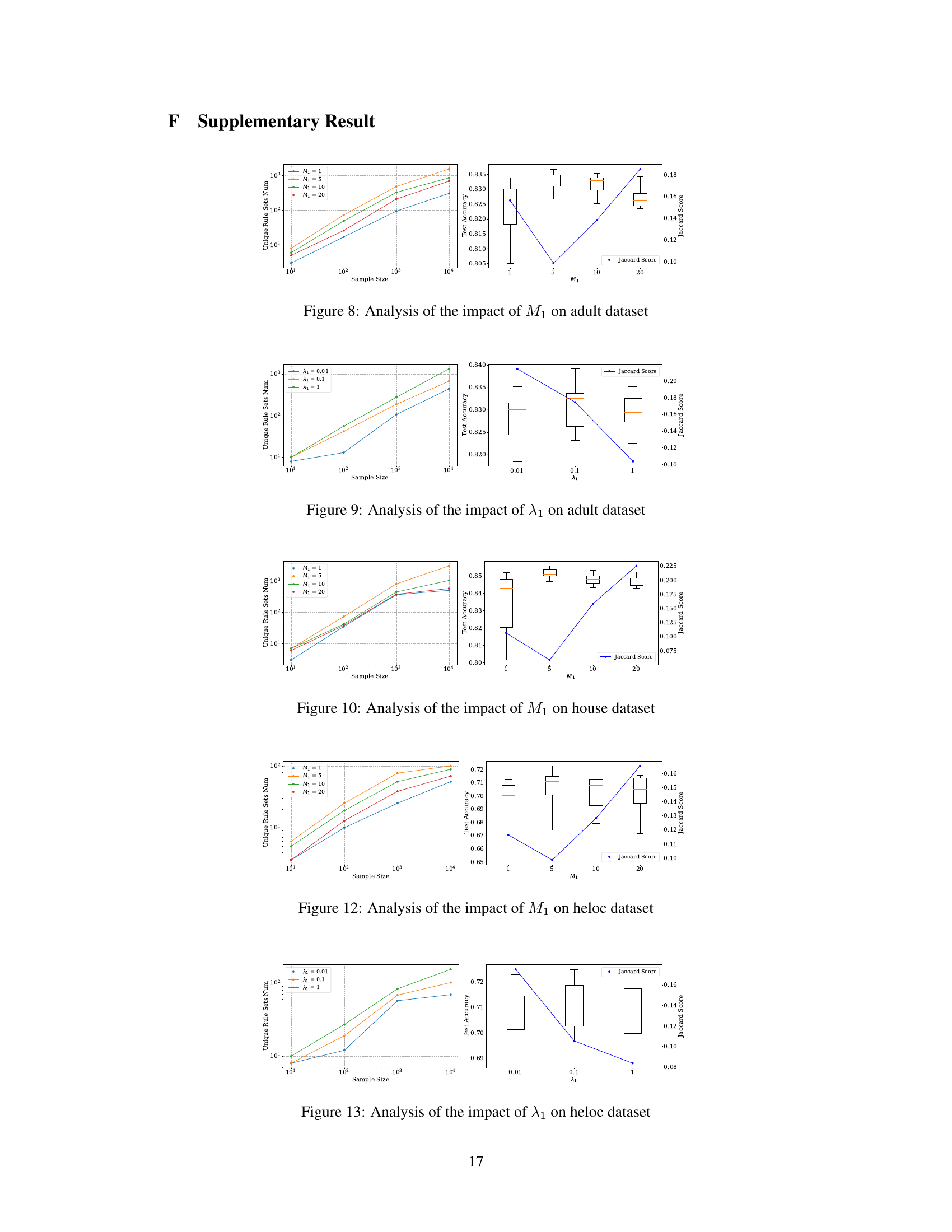
This figure analyzes how the hyperparameter M₁, which controls the number of weight samples generated by the hypernetwork, affects the performance of HyperLogic on the magic dataset. The left panel shows the number of unique rule sets generated as a function of the number of samples drawn, for different values of M₁. The right panel shows the test accuracy and Jaccard similarity (a measure of rule set diversity) as a function of M₁. The results suggest that an intermediate value of M₁ (around 5) provides a good balance between the diversity of the rule sets and the accuracy of the model.
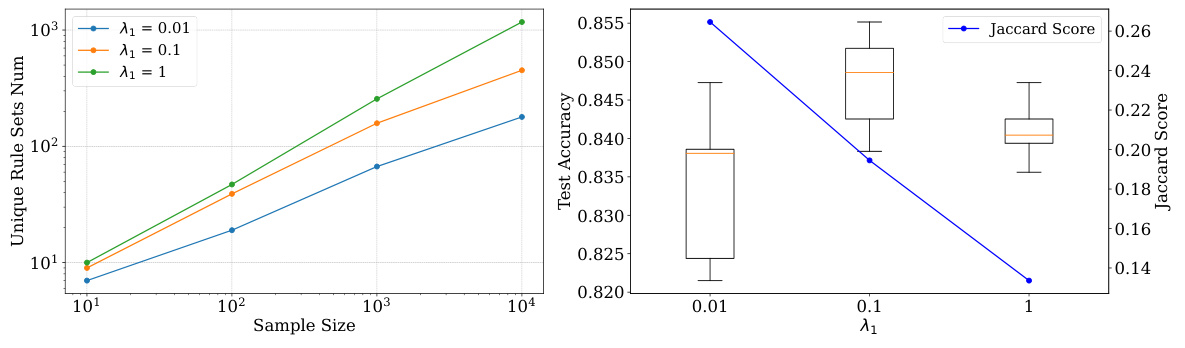
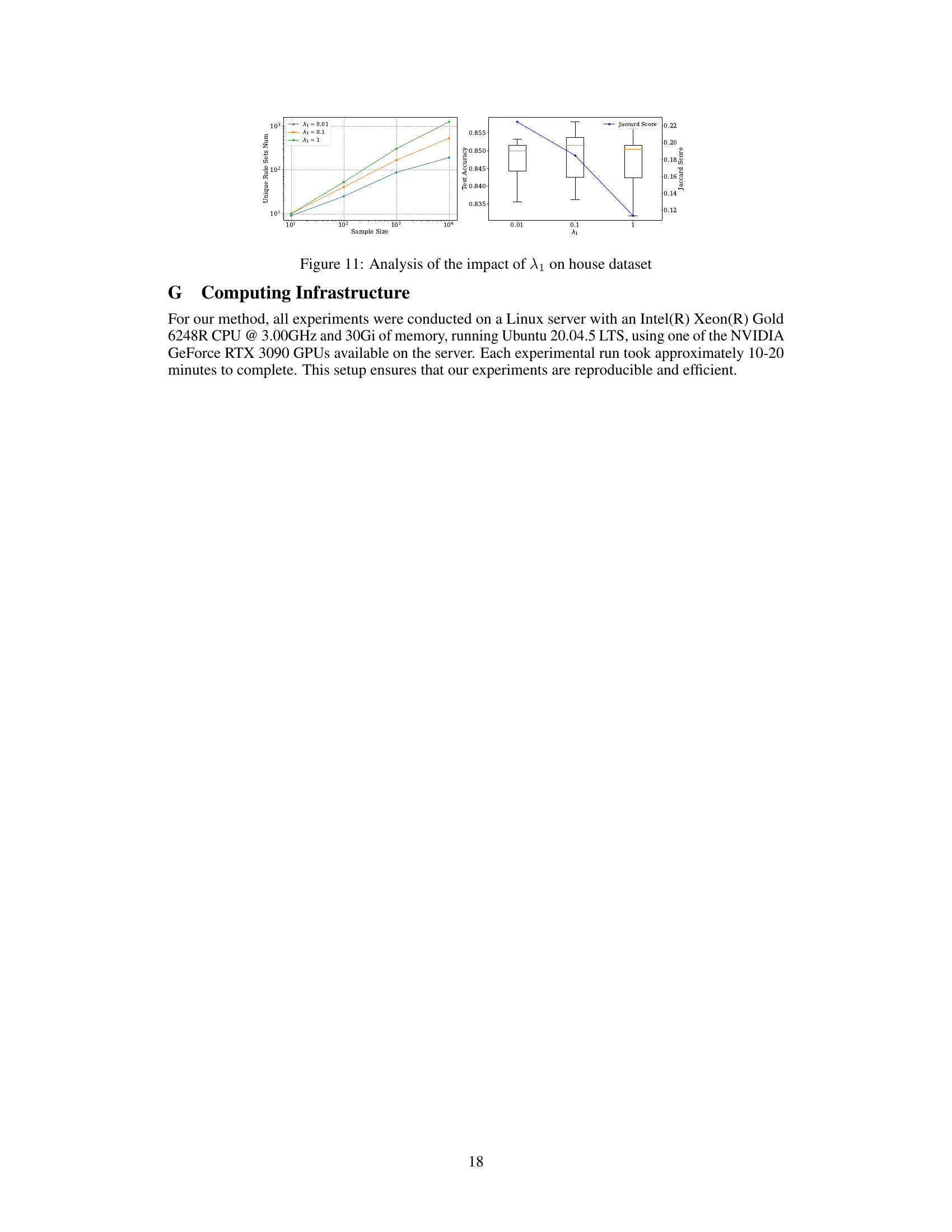
This figure analyzes how the hyperparameter λ₁, which controls the diversity regularization in the HyperLogic model, affects the number of unique rule sets generated, the test accuracy of the model, and the Jaccard similarity score between those rule sets. The left panel shows that increasing λ₁ leads to a greater number of unique rule sets generated. The right panel indicates a trade-off; while a larger λ₁ increases the diversity of rule sets (higher Jaccard score), it can slightly decrease the test accuracy, suggesting that an optimal balance needs to be found.

This figure displays the test accuracy achieved by using ensemble learning with varying numbers (L) of top-performing rule sets. The test accuracy is initially observed to increase as L increases, suggesting that the combination of diverse rule sets enhances the overall performance. However, after a certain point, increasing L leads to slightly reduced test accuracy. This indicates that incorporating an excessive number of rule sets can negatively impact the overall prediction accuracy, possibly due to overfitting or interference amongst rule sets.
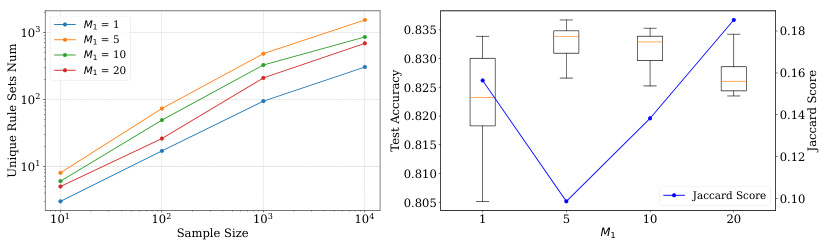
This figure analyzes how the hyperparameter M₁ (number of weight samples in the training stage) impacts the performance of HyperLogic on the MAGIC dataset. The left panel shows the number of unique rule sets generated as a function of the sample size for different values of M₁. The right panel displays boxplots of the test accuracy and Jaccard similarity score for varying M₁, illustrating the trade-off between diversity and accuracy. A small M₁ might not fully explore the parameter space during training, potentially affecting diversity and accuracy. Conversely, a large M₁ increases the number of rules but may not significantly enhance the performance and potentially cause overfitting. The optimal M₁ value appears to balance this trade-off, yielding both diverse rule sets and high accuracy.

This figure analyzes how the hyperparameter λ₁, which controls diversity regularization, affects the number of unique rule sets generated, test accuracy, and Jaccard similarity scores. The x-axis represents the number of samples drawn from the hypernetwork. Three lines show the results for different values of λ₁ (0.01, 0.1, and 1). The left subplot shows that as λ₁ increases, the number of unique rule sets generated also increases, indicating that higher values of λ₁ promote greater diversity. The right subplot shows that while increased λ₁ leads to greater diversity (lower Jaccard similarity), it can negatively impact test accuracy after reaching a peak.
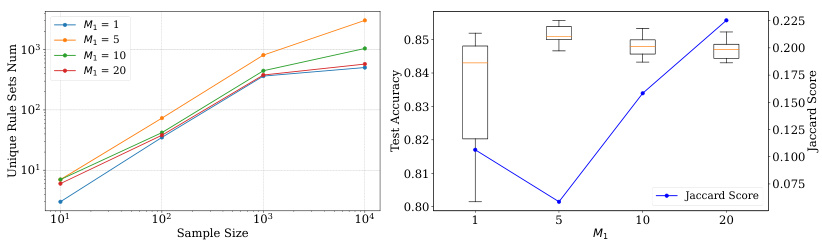
This figure analyzes how the hyperparameter M₁ (number of weight samples to approximate the expectation) affects the performance of HyperLogic on the MAGIC dataset. The left panel shows the number of unique rule sets generated as the sample size increases for different values of M₁. The right panel shows the test accuracy and Jaccard similarity (a measure of rule set diversity) for the different values of M₁. It demonstrates that a small value of M₁ (such as 5) strikes a good balance between diversity and accuracy.
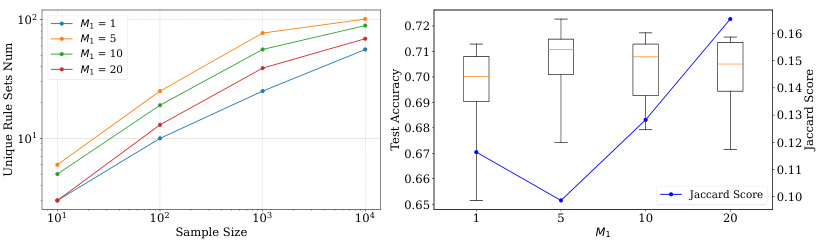
This figure analyzes how the hyperparameter M₁ (number of weight samples to approximate the expectation) affects the performance of HyperLogic on the MAGIC dataset. The left panel shows the number of unique rule sets generated as the sample size increases for different values of M₁. The right panel shows box plots of the test accuracy and a line plot of the Jaccard similarity score for the generated rules across varying M₁ values. This illustrates the trade-off between rule diversity (indicated by the number of unique rule sets and Jaccard score) and accuracy.
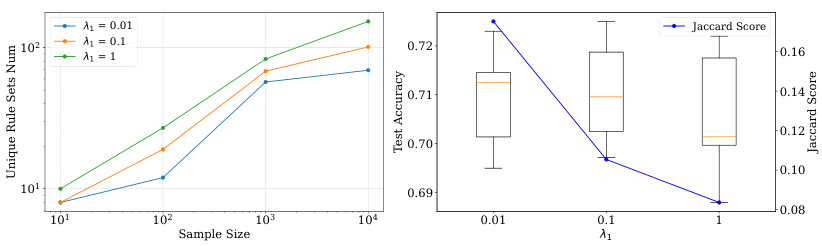
The figure analyzes how the hyperparameter λ₁, which controls the diversity regularization, affects the diversity and accuracy of the generated rules in the MAGIC dataset. The left subplot shows the number of unique rule sets generated as the sample size increases for different values of λ₁. The right subplot presents a box plot of the test accuracy and the Jaccard similarity (a measure of diversity) across different values of λ₁. The results indicate that increasing λ₁ leads to greater rule set diversity but might slightly decrease the accuracy.

This figure analyzes how the hyperparameter λ₁, which controls the diversity regularization in the HyperLogic model, affects the number of unique rule sets generated and the model’s test accuracy. The left panel shows that as the sample size increases, the number of unique rule sets generated increases for all values of λ₁. However, the increase is steeper for higher values of λ₁ indicating that increasing λ₁ leads to a greater diversity of rule sets. The right panel shows that while a higher λ₁ leads to increased diversity (as measured by Jaccard similarity), it also slightly decreases the model’s test accuracy. This suggests there’s a tradeoff between the diversity of rules generated and their overall predictive accuracy.
More on tables
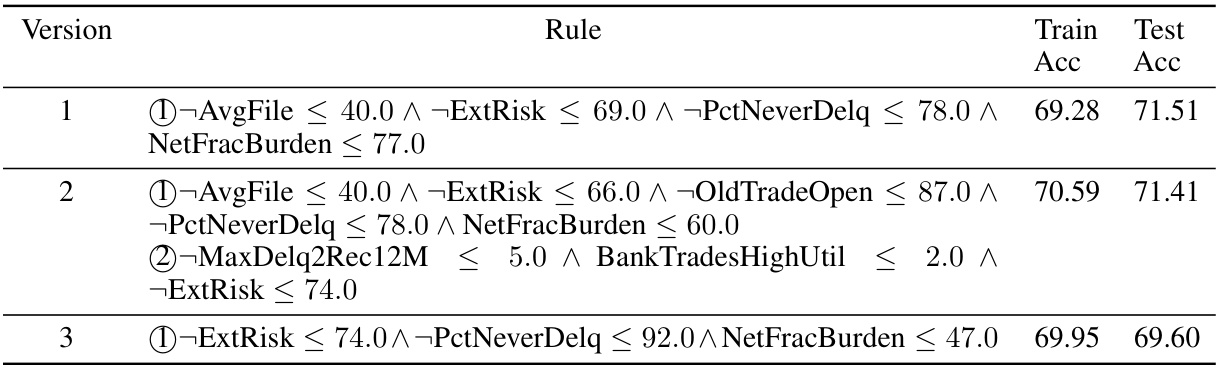
This table presents three different optimal rule sets obtained from three separate training sessions using the HyperLogic model on the HELOC dataset. Each rule set includes a set of logical rules aiming to predict a binary outcome. The ‘Train Acc’ and ‘Test Acc’ columns show the training and testing accuracy of each version. The variations between versions highlight the ability of HyperLogic to uncover multiple diverse, high-performing rule sets for the same task, which would not be accessible using a standard approach limited to producing a single set of rules.
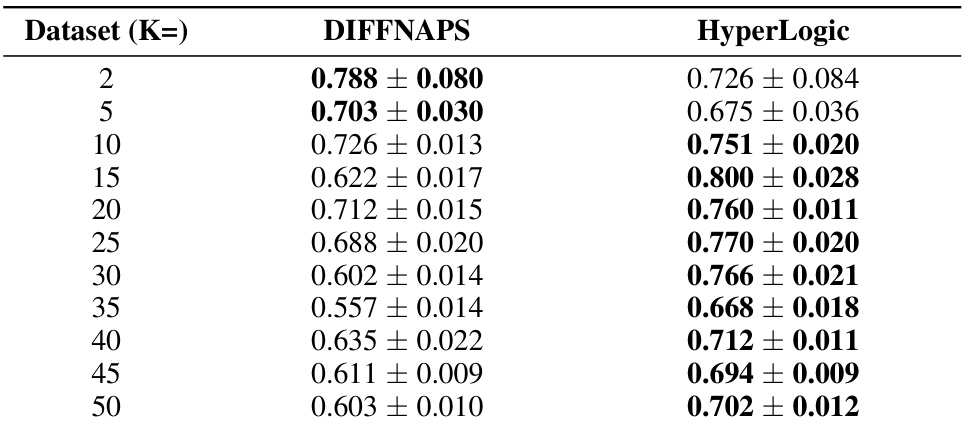
This table presents the F1 scores achieved by DIFFNAPS and HyperLogic on 11 synthetic datasets with varying numbers of categories (K). Each dataset is tested with a fixed input dimension of 5000, and each category contains 1000 samples. The F1 score, a measure of a test’s accuracy, is presented with its standard deviation, allowing for a statistical comparison of the two methods’ performance across different dataset complexities.
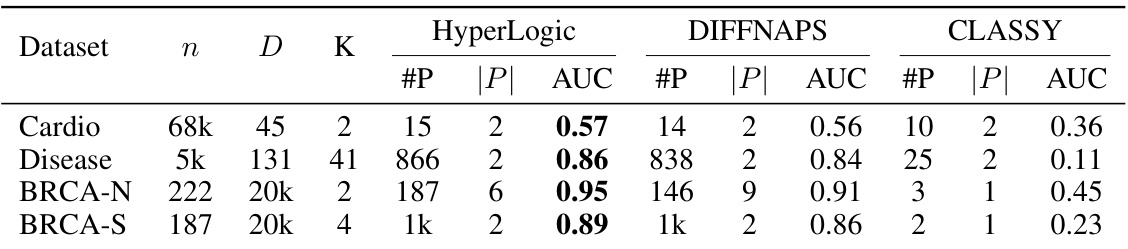
This table compares the performance of HyperLogic against two other methods, DIFFNAPS and CLASSY, on four real-world biological datasets. It shows the number of samples (n), features (D), and classes (K) in each dataset, along with the number of discovered patterns (#P), average pattern length (|P|), and Area Under the Curve (AUC) score achieved by each method. The results indicate HyperLogic’s competitive performance, particularly on larger datasets.
Full paper#