TL;DR#
Current language models (LMs) often fail to grasp the hierarchical nature of language, hindering their performance on tasks needing transitive inference or hierarchical knowledge transfer. This is a major limitation as many real-world concepts and knowledge domains are inherently hierarchical.
To address this, the researchers introduce Hierarchy Transformer Encoders (HITs), a novel approach that retrains transformer-based LMs in hyperbolic space. This space’s expansive nature is well-suited for hierarchical data. HITs utilize hyperbolic clustering and centripetal losses to effectively cluster and organize related entities hierarchically. The results show that HITs consistently outperform existing models on various tasks, demonstrating the effectiveness and transferability of the proposed approach. This work makes a substantial contribution by providing a novel solution to enhance the hierarchical reasoning capabilities of language models.
Key Takeaways#
Why does it matter?#
This paper is crucial because it directly addresses a major limitation of current language models—their inability to effectively understand and utilize hierarchical structures in language. By introducing a novel re-training method (HITs) that leverages hyperbolic geometry, the research significantly advances the field by improving models’ performance on tasks requiring transitive inference and hierarchical knowledge transfer. This opens exciting new avenues for future research and has significant implications for various NLP applications.
Visual Insights#
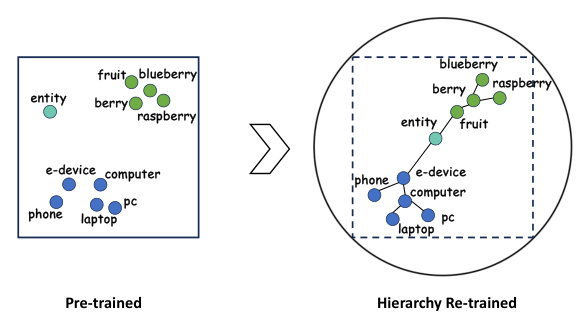
🔼 This figure illustrates the difference between the output embedding space of pre-trained transformer language models and the proposed Hierarchy Transformer Encoder (HIT). Pre-trained models use a tanh activation function which confines their output embeddings within a d-dimensional hypercube. The HIT model maps the output embeddings to a Poincaré ball, a hyperbolic space better suited for representing hierarchies. The Poincaré ball has a radius of √d, and its boundary circumscribes the hypercube. This allows HIT to explicitly model hierarchies using hyperbolic clustering and centripetal losses, as shown in the right panel by the clustered and hierarchically organized entities.
read the caption
Figure 1: Illustration of how hierarchies are explicitly encoded in HITs. The square (d-dimensional hyper-cube) refers to the output embedding space of transformer encoder-based LMs whose final activation function is typically tanh, and the circumscribed circle (d-dimensional hyper-sphere) refers to the Poincaré ball of radius √d. The distance and norm metrics involved in our hyperbolic losses are defined w.r.t. this manifold.
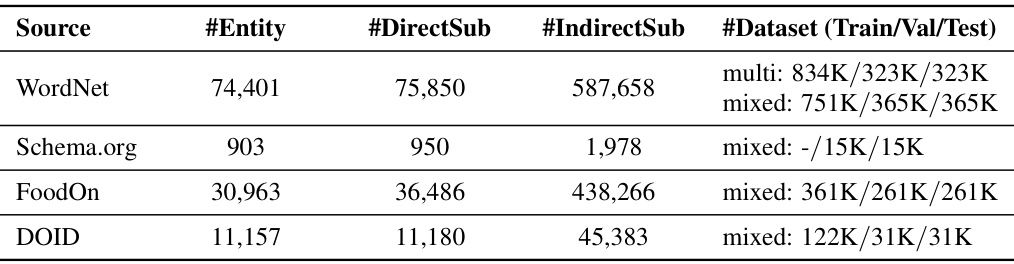
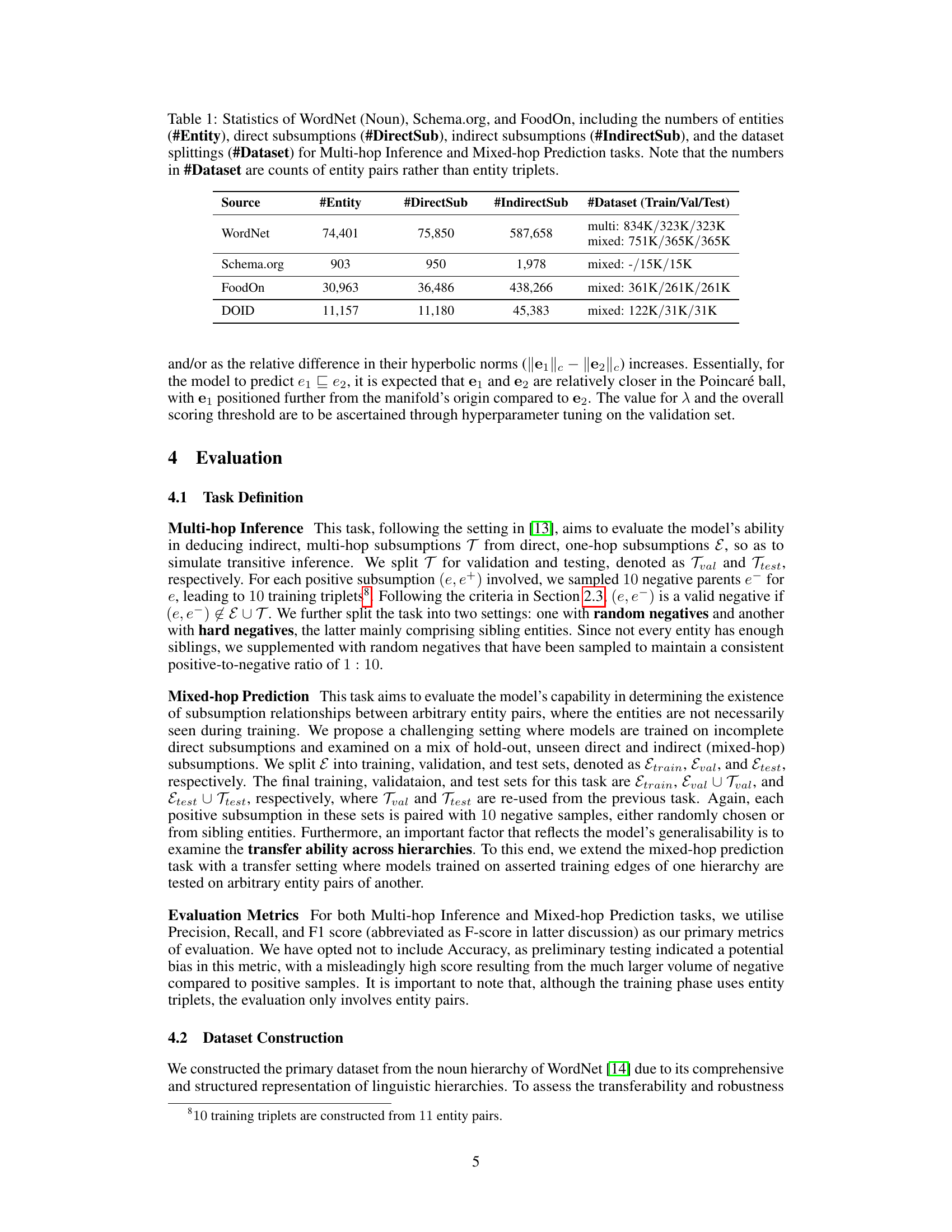
🔼 This table presents the statistics of four datasets used in the paper’s experiments: WordNet (Noun), Schema.org, FoodOn, and DOID. For each dataset, it shows the number of entities, direct subsumptions (one-hop relationships), indirect subsumptions (multi-hop relationships), and the dataset split into training, validation, and testing sets for both Multi-hop Inference and Mixed-hop Prediction tasks. The numbers in the ‘#Dataset’ column represent the number of entity pairs, not triplets.
read the caption
Table 1: Statistics of WordNet (Noun), Schema.org, and FoodOn, including the numbers of entities (#Entity), direct subsumptions (#DirectSub), indirect subsumptions (#IndirectSub), and the dataset splittings (#Dataset) for Multi-hop Inference and Mixed-hop Prediction tasks. Note that the numbers in #Dataset are counts of entity pairs rather than entity triplets.
In-depth insights#
Hyperbolic LM Retraining#
Retraining language models (LMs) within a hyperbolic space offers a novel approach to explicitly encode hierarchical structures inherent in language, a limitation of current LMs. This hyperbolic LM retraining method leverages the expansive nature of hyperbolic geometry to effectively organize and cluster semantically related entities. By situating the output embeddings of pre-trained LMs in a Poincaré ball, with curvature adapting to embedding dimension, and training with hyperbolic clustering and centripetal losses, the method enhances the model’s capacity to simulate transitive inference and predict hierarchical relationships. The use of hyperbolic losses is particularly crucial, as they encourage the formation of clusters reflecting hierarchical relationships, thereby overcoming the limitations of traditional Euclidean embedding approaches. The effectiveness and transferability of this approach is demonstrated through improved performance on tasks such as multi-hop inference and mixed-hop prediction, showcasing its potential for various NLP applications that involve hierarchical data.
Transitive Inference#
Transitive inference, the ability to deduce implicit relationships based on explicitly stated ones, is a crucial aspect of higher-order reasoning. In the context of language models, successful transitive inference demonstrates a deeper understanding of hierarchical structures and semantic relationships within a knowledge base. The paper likely investigates how well a language model, possibly through a novel training technique, can perform transitive inference tasks. Benchmarking the model’s performance against pre-trained models highlights the effectiveness of the new approach in capturing these complex relationships. The results might show improved accuracy in inferring unseen relationships compared to standard models, indicating a more nuanced comprehension of hierarchical knowledge. A key point to consider is whether the model truly understands the transitive relationship or simply memorizes patterns from the training data. The study likely probes for genuine understanding through careful task design and testing, evaluating the model’s ability to generalize to novel scenarios and unseen data points. Ultimately, the analysis of transitive inference results offers insights into the model’s cognitive capabilities and its potential applications in knowledge representation and reasoning.
Hierarchy Encoding#
The concept of ‘Hierarchy Encoding’ in the context of language models centers on the challenge of effectively representing hierarchical structures inherent in human language. Traditional language models often struggle with this, exhibiting limitations in capturing transitive inference and simulating hierarchical reasoning tasks. The proposed approach tackles this by leveraging hyperbolic geometry, a non-Euclidean space particularly well-suited to encode hierarchical relationships. By situating word embeddings within a Poincaré ball, and employing specific losses like hyperbolic clustering and centripetal loss, the model is trained to explicitly represent hierarchical information. This method surpasses traditional approaches by effectively clustering related entities and positioning them hierarchically based on their semantic distance. Importantly, this results in improved performance on tasks requiring hierarchical understanding, demonstrating the effectiveness of the proposed hyperbolic hierarchy encoding method and its potential in addressing the limitations of previous methods. The approach’s success underscores the significance of incorporating explicit hierarchical representations in language models for enhanced performance in various NLP applications. Further research could explore expanding this work to diverse datasets and evaluating it against other specialized hierarchy encoding techniques.
Hyperbolic Losses#
The concept of “Hyperbolic Losses” in the context of hierarchical structure learning within language models is a crucial innovation. It leverages the properties of hyperbolic geometry, specifically its ability to efficiently represent hierarchical relationships, to improve model performance. The approach likely involves defining losses that penalize embeddings that violate hierarchical constraints within a hyperbolic space. Two key losses are probable: a clustering loss that pulls semantically similar entities closer and pushes dissimilar entities farther apart, and a centripetal loss that ensures that higher-level (more general) entities are positioned closer to the origin of the hyperbolic space than lower-level (more specific) entities. The choice of hyperbolic space allows for the representation of hierarchical information in a way that’s not easily achievable in Euclidean space. The curvature of the hyperbolic space could be dynamically adjusted, potentially based on embedding dimensions, further enhancing the model’s ability to adapt to varying hierarchical complexities. The effectiveness of this method relies heavily on the careful design and weighting of these losses and how they interact during the training process. Successful implementation results in embeddings that naturally reflect the hierarchical structure of the data, allowing for improved knowledge transfer and inference tasks.
Future Work#
The paper’s ‘Future Work’ section suggests several promising avenues. Addressing catastrophic forgetting during hierarchy re-training is crucial, as this could impact the model’s overall language understanding. Investigating methods to handle entity naming ambiguity is also important; this would improve the robustness of the approach and reduce noise. The authors also propose extending HIT to handle multiple hierarchies and to incorporate multiple types of hierarchical relationships simultaneously to increase the model’s general applicability. Finally, developing a hierarchy-based semantic search leveraging the HIT model’s capabilities is highlighted as a valuable direction for future research. This would create a new paradigm in semantic search that could significantly improve performance and efficiency. These are all impactful suggestions that would enhance the model’s practicality and effectiveness.
More visual insights#
More on figures

🔼 This figure illustrates the effect of the proposed hyperbolic loss function (LHIT) on the learned entity embeddings. In Euclidean space, the forces pulling sibling entities (phone/computer, laptop/pc) toward their parent (e-device) while pushing them apart from each other would be contradictory. However, the hyperbolic space allows this, as distances grow exponentially towards the boundary, making it suitable for hierarchical structures.
read the caption
Figure 2: Illustration of the impact of LHIT during training. In Euclidean space, it seems contradictory that both 'phone' and 'computer' are pulled towards 'e-device' but are also pushed away from each other. However, in principle this is not a problem in hyperbolic space, where distances increase exponentially relative to Euclidean distances as one moves from the origin to the boundary of the manifold.

🔼 This histogram shows the distribution of hyperbolic norms for WordNet entities embedded using the Hierarchy Transformer encoder (HIT). The x-axis represents the hyperbolic norm, and the y-axis represents the count of entities with that norm. The distribution shows an exponential rise in the number of child entities, with a sharp decline in entities beyond a norm of approximately 23, indicating that few entities reside at the highest hierarchical levels. The relatively small range of norms (approximately 8 to 24) suggests that HIT effectively accommodates all WordNet entities within a limited region of the high-dimensional manifold.
read the caption
Figure 3: Distribution of WordNet entity embeddings generated by HIT w.r.t. their hyperbolic norms.
More on tables
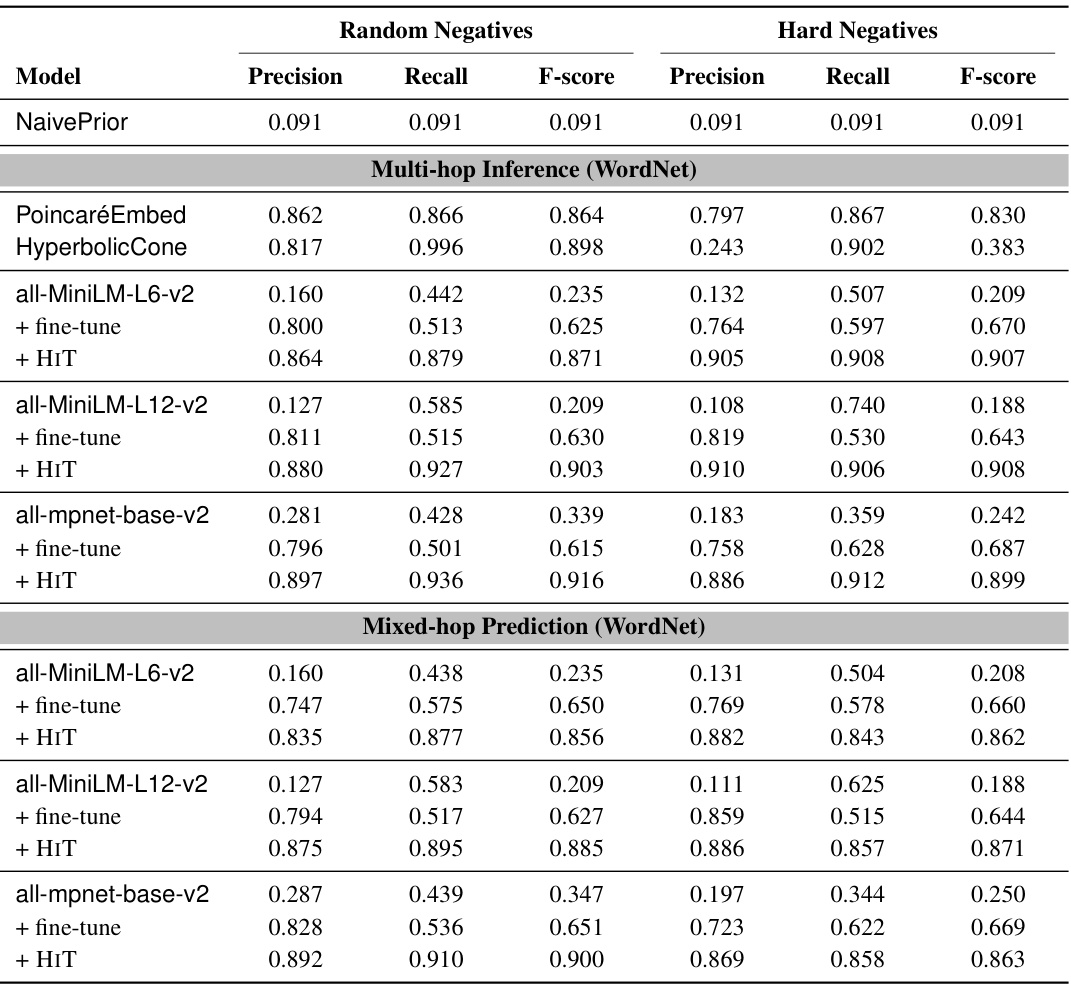
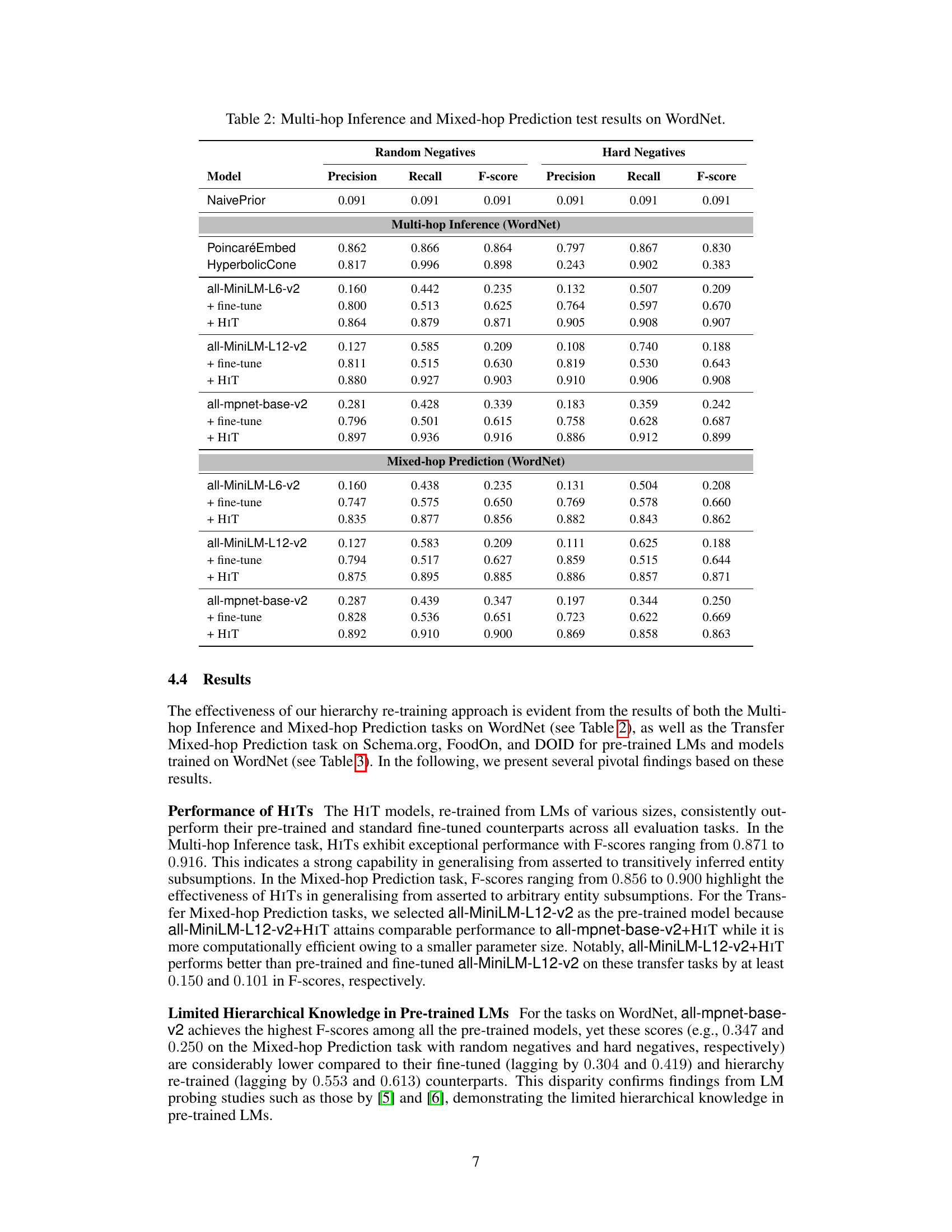
🔼 This table presents the results of the Multi-hop Inference and Mixed-hop Prediction tasks performed on the WordNet dataset. It compares the performance of several models, including pre-trained Language Models (LMs), fine-tuned LMs, and HIT models (Hierarchy Transformer encoders, the authors’ proposed method) across different experimental settings. These settings involve random negative samples and hard negative samples (sibling entities) used during the training process. The metrics used for comparison are Precision, Recall, and F-score. The table shows how HIT models consistently outperform baseline models across various scenarios.
read the caption
Table 2: Multi-hop Inference and Mixed-hop Prediction test results on WordNet.
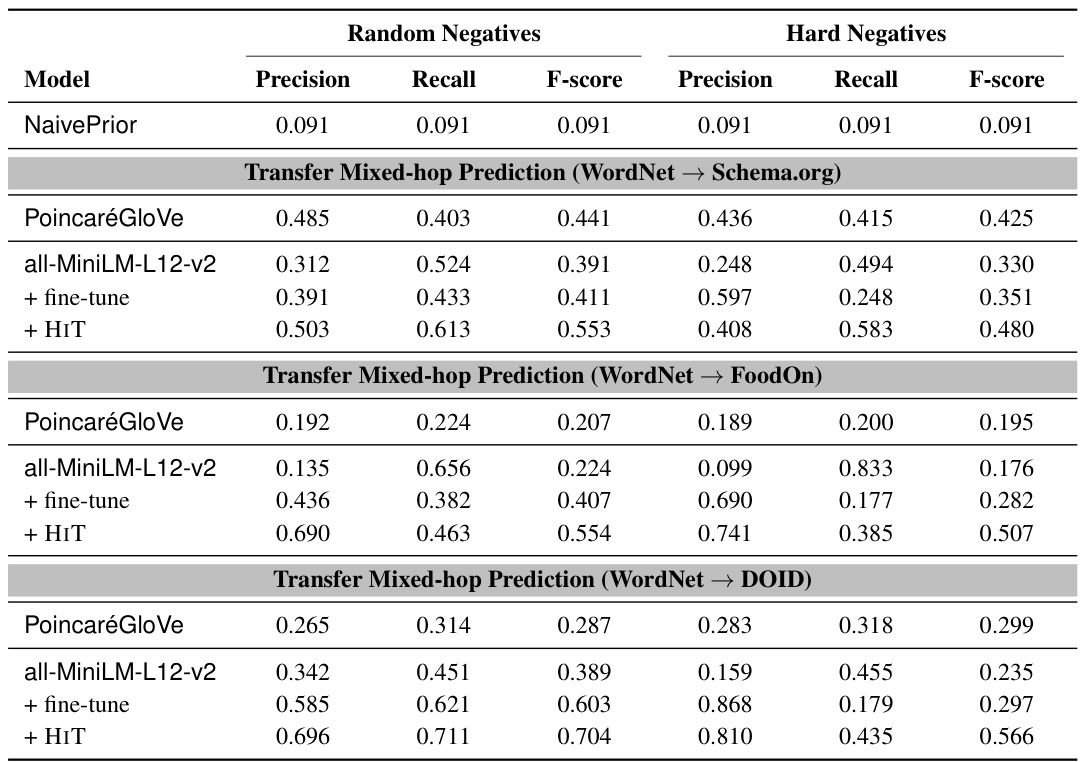
🔼 This table presents the results of the transfer learning experiments. The models were trained on WordNet and evaluated on three other ontologies (Schema.org, FoodOn, and DOID). The table shows the precision, recall, and F-score for both random and hard negative samples. The purpose is to assess how well models trained on one hierarchy generalize to other, unseen hierarchies.
read the caption
Table 3: Transfer Mixed-hop Prediction test results on Schema.org, FoodOn, and DOID.

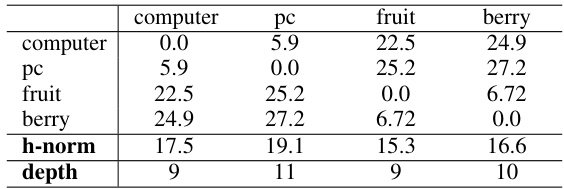
🔼 This table presents the Pearson correlation coefficients between the hyperbolic norms of entities and their depths in the WordNet hierarchy for three different hyperbolic models: HIT, PoincaréEmbed, and HyperbolicCone. The correlation coefficient measures the linear relationship between the two variables. A higher correlation coefficient indicates a stronger linear relationship. The results show that all three models exhibit a positive correlation, indicating that entities with higher depths (further down the hierarchy) tend to have higher hyperbolic norms, which is expected.
read the caption
Table 4: Statistical correlations between WordNet entities' depths and their hyperbolic norms across different hyperbolic models.
🔼 This table presents the results of Multi-hop Inference and Mixed-hop Prediction tasks performed on the WordNet dataset. It compares the performance of different models, including pre-trained Language Models (LMs), fine-tuned LMs, and the proposed Hierarchy Transformer encoders (HITs), across two negative sampling strategies: random negatives and hard negatives. The metrics used for evaluation are Precision, Recall, and F1-score (F-score). The results demonstrate the superiority of the HIT models, particularly in the hard negative setting, signifying their robustness in generalising from asserted to both inferred and unseen subsumption relationships.
read the caption
Table 5: Multi-hop Inference and Mixed-hop Prediction test results on WordNet.

🔼 This table shows the impact of varying the hyperparameters (loss margins α and β) on the performance of the allMiniLM-L12-v2+HIT model, specifically on the WordNet Mixed-hop Prediction task. It demonstrates the model’s robustness to changes in these hyperparameters, indicating consistent high performance even with different values.
read the caption
Table 6: Ablation results (F-score) of allMiniLM-L12-v2+HIT on WordNet’s Mixed-hop Prediction.

🔼 This table presents the statistics of the SNOMED CT hierarchy, including the number of entities, direct and indirect subsumptions, and the dataset split for both multi-hop inference and mixed-hop prediction tasks. It shows the counts of entity pairs (not triplets).
read the caption
Table 7: Statistics of SNOMED-CT, including the numbers of entities (#Entity), direct subsumptions (#DirectSub), indirect subsumptions (#IndirectSub), and the dataset splittings (#Dataset) for Multi-hop Inference and Mixed-hop Prediction tasks.
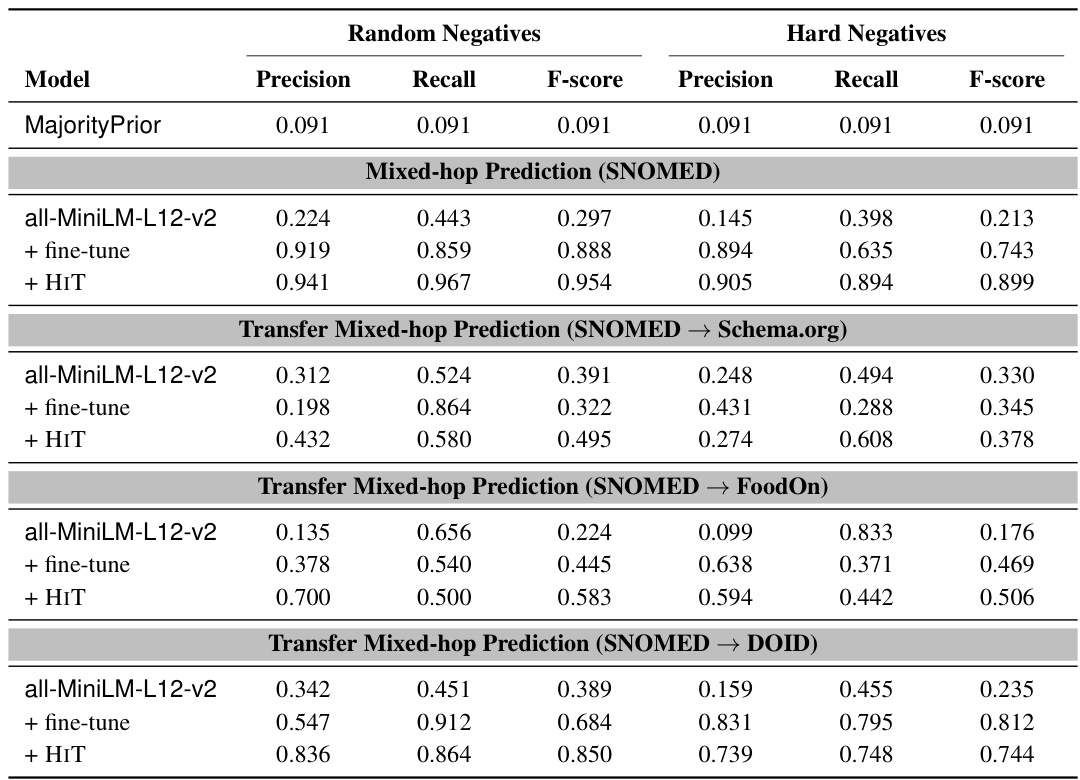
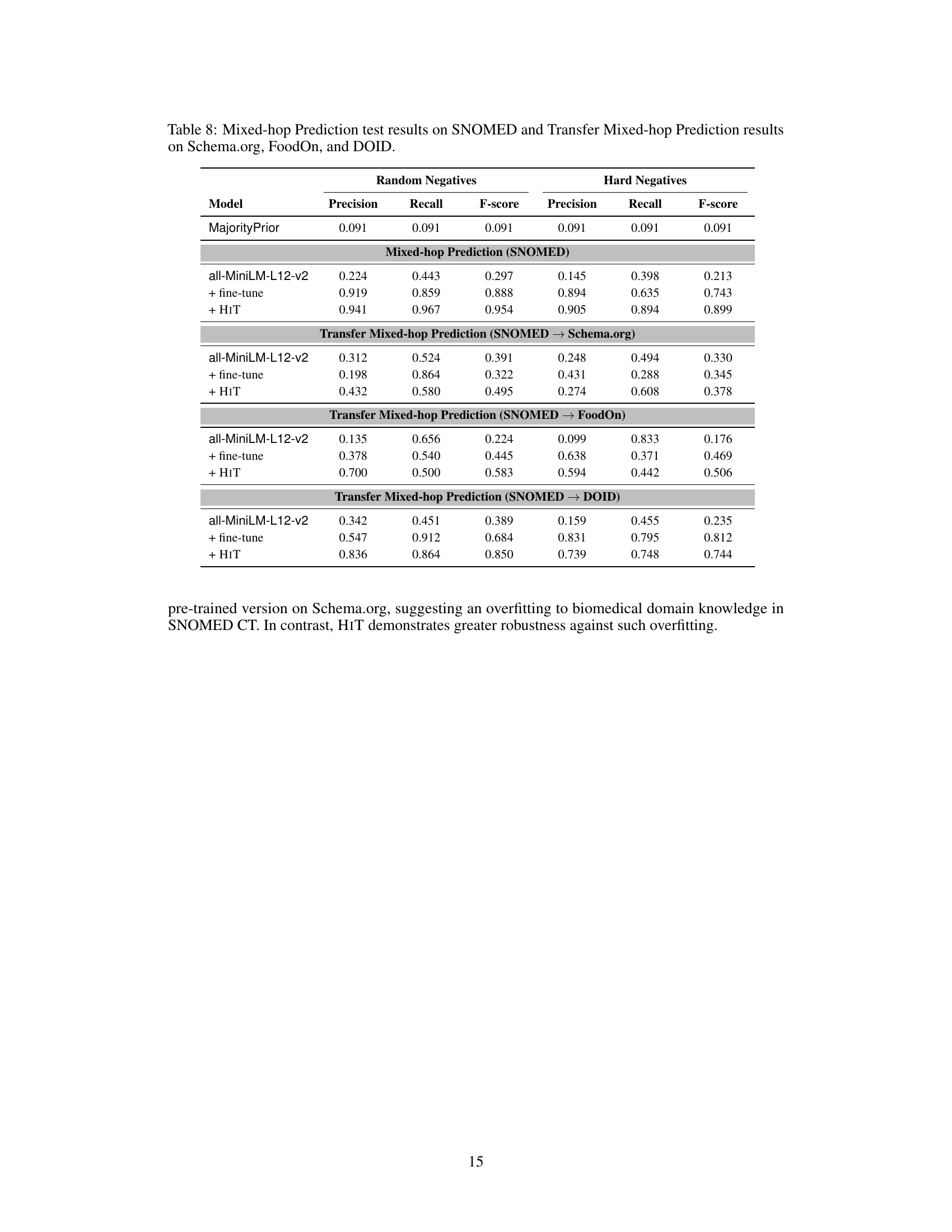
🔼 This table presents the results of the Mixed-hop Prediction task on the SNOMED CT ontology, along with transfer learning results to other ontologies (Schema.org, FoodOn, and DOID). It compares the performance of three models: the pre-trained all-MiniLM-L12-v2 model, the fine-tuned version of this model, and the HIT (Hierarchy Transformer) model. Results are shown separately for random and hard negative samples, indicating the performance metrics (Precision, Recall, and F-score) for each model on each dataset. The table highlights the effectiveness of HIT in handling various datasets and the robustness against overfitting.
read the caption
Table 8: Mixed-hop Prediction test results on SNOMED and Transfer Mixed-hop Prediction results on Schema.org, FoodOn, and DOID.
Full paper#