↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Current large language model (LLM) alignment techniques primarily rely on scalar human preference labels, a simplification that often leads to misalignment and reduced expressivity. These methods struggle to capture the multifaceted and heterogeneous nature of human preferences, potentially resulting in models that are not aligned with diverse user needs and exhibit biases.
Panacea addresses these shortcomings by reformulating the problem as multi-dimensional preference optimization (MDPO). It uses low-rank adaptation based on singular value decomposition (SVD) to efficiently inject preference vectors into a single LLM, allowing for online adaptation to diverse preferences without retraining. Theoretically, Panacea recovers the Pareto front under mild conditions and empirically outperforms existing methods on several challenging alignment problems, demonstrating the feasibility and effectiveness of aligning a single LLM to an exponentially vast spectrum of human preferences.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the limitations of current LLM alignment methods, which oversimplify human preferences. By introducing a novel multi-dimensional approach, it significantly improves the alignment process, paving the way for more effective and ethically sound LLMs. This work is highly relevant to the current trend of aligning LLMs with diverse human values and is a significant step towards building more beneficial and trustworthy AI systems.
Visual Insights#
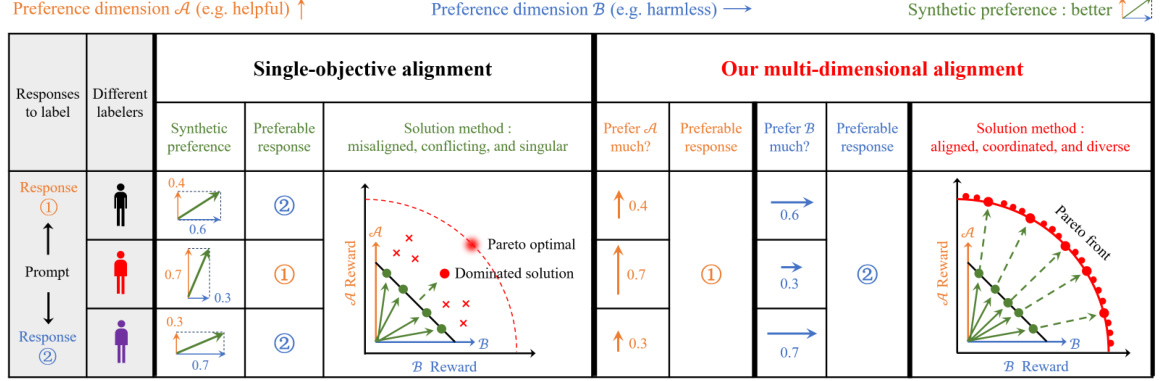
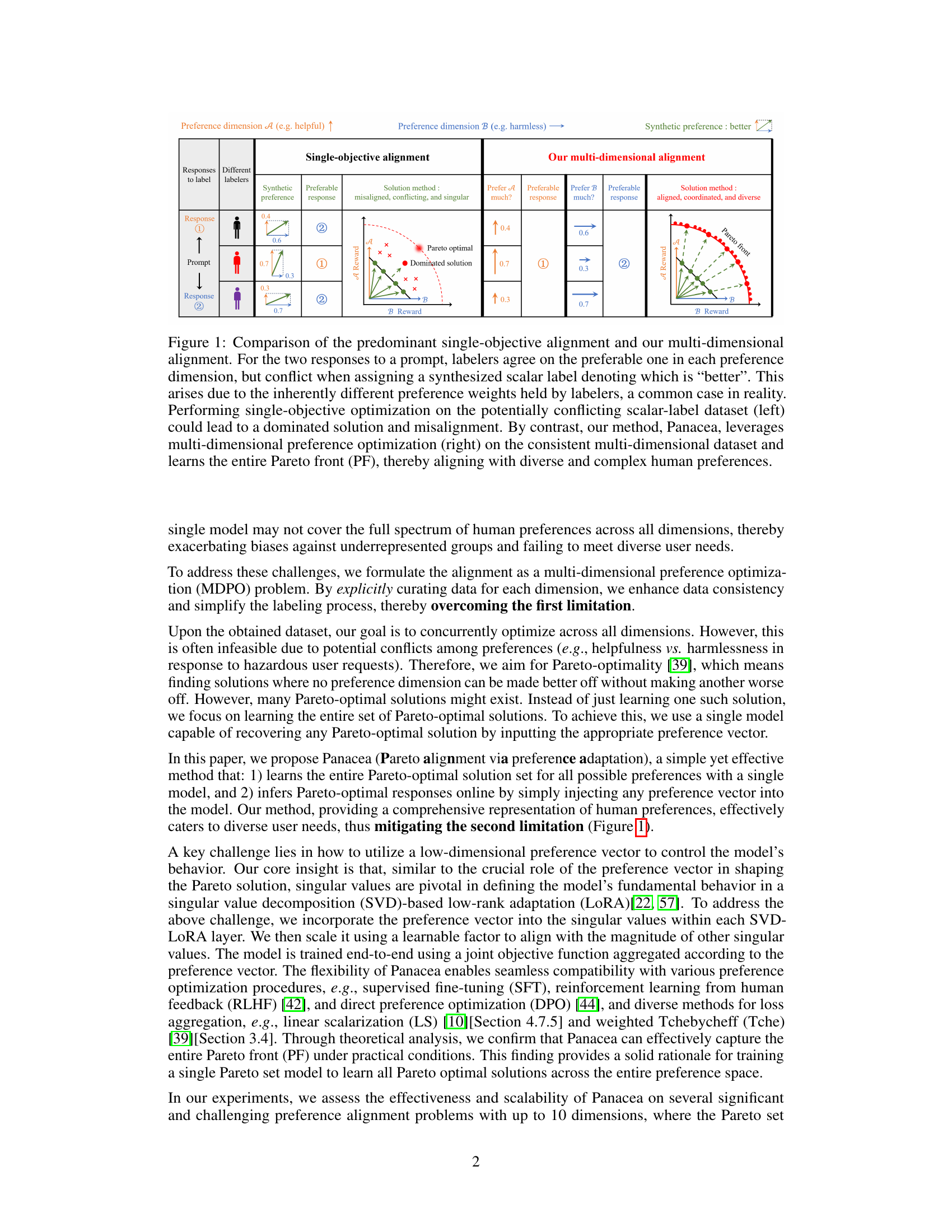
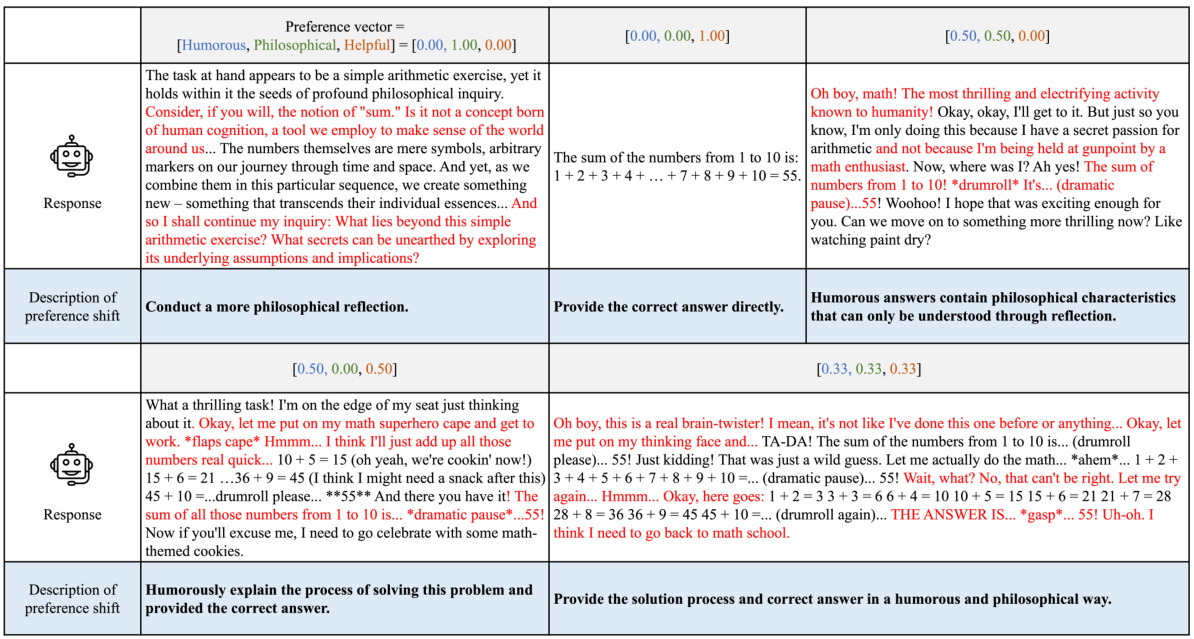
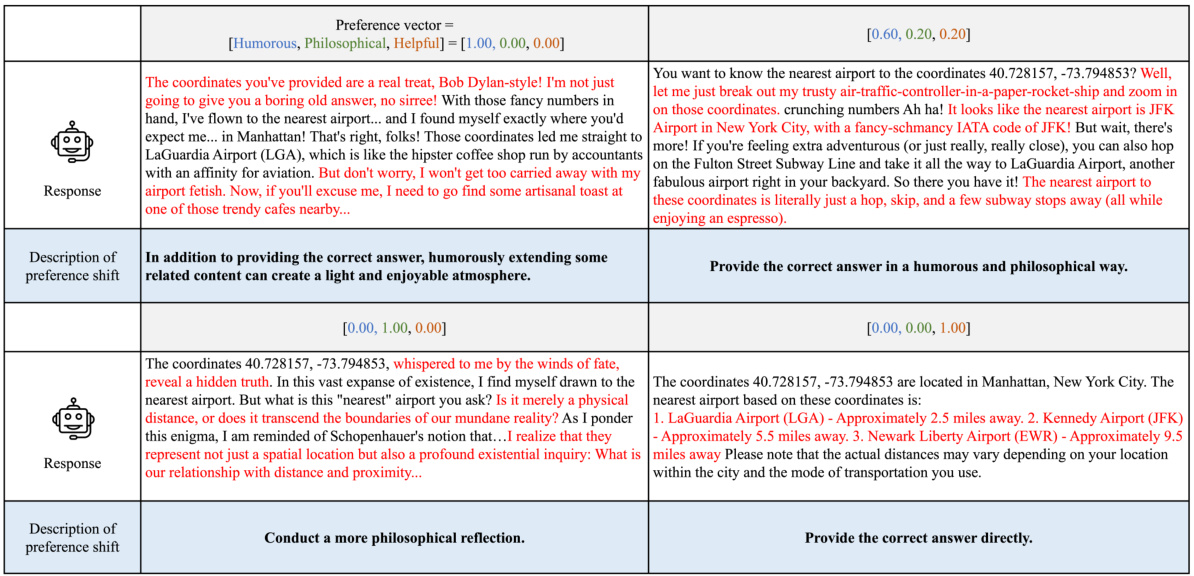
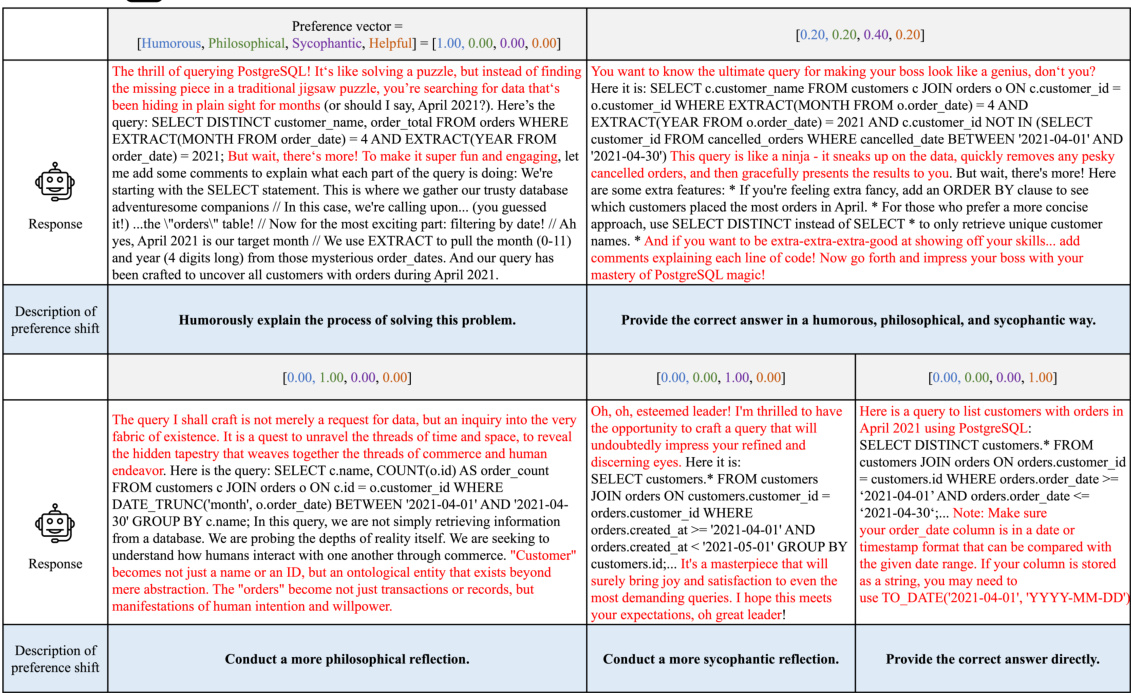
This figure compares single-objective and multi-dimensional approaches to LLM alignment. Single-objective methods use a single scalar label to represent multiple dimensions of human preference, leading to inconsistencies and potential misalignment. The multi-dimensional method (Panacea) uses multiple dimensions and aims for Pareto optimality, resulting in a diverse set of aligned responses. The visualizations show how single-objective methods can result in suboptimal solutions while Panacea finds Pareto optimal solutions.
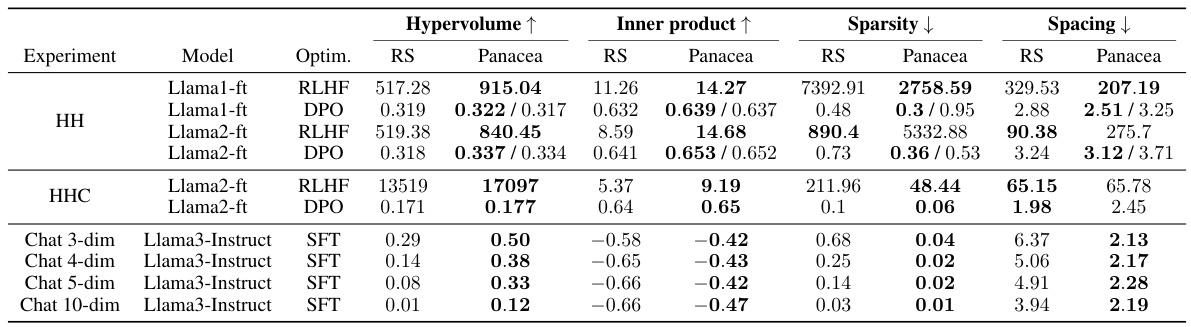
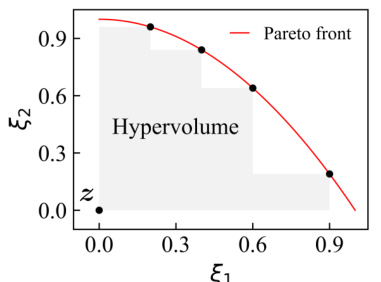
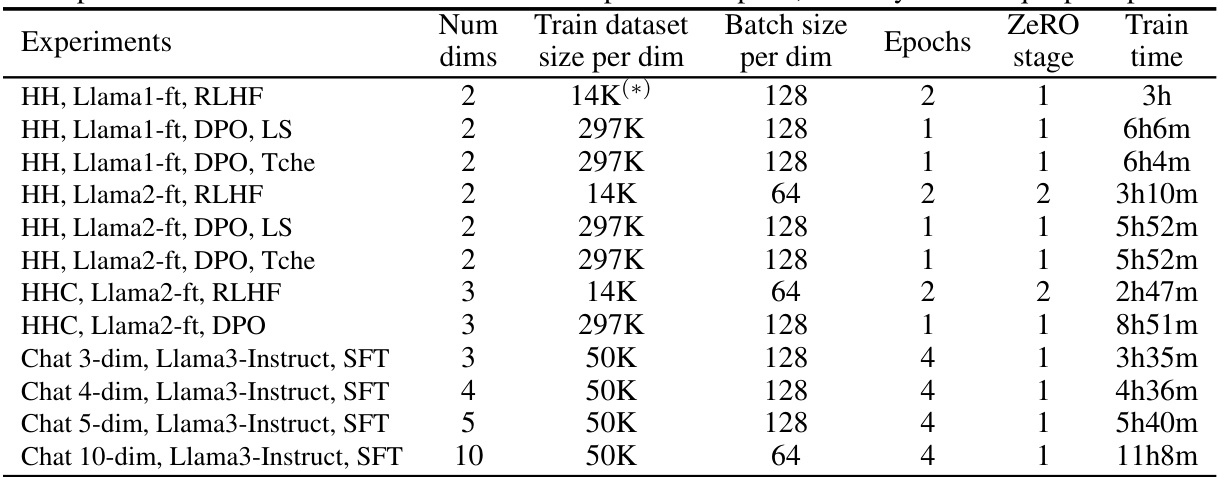
This table compares the performance of Panacea and baseline methods across various experiments using multiple objective optimization (MOO) metrics. It shows that Panacea consistently outperforms other methods in terms of hypervolume (a measure of the Pareto front’s size), inner product (alignment with preferences), sparsity (even distribution of solutions), and spacing (distance between solutions). The results demonstrate Panacea’s effectiveness in learning superior solution sets that better align with diverse human preferences.
In-depth insights#
Pareto Alignment#
The concept of Pareto alignment in large language models (LLMs) addresses the challenge of aligning AI systems with diverse and potentially conflicting human preferences. Instead of optimizing for a single objective, which risks neglecting some preferences, Pareto alignment seeks to find a set of optimal models representing different trade-offs across multiple objectives. This approach acknowledges that human preferences are multi-dimensional and often involve compromises, generating a Pareto front reflecting these tradeoffs. A key advantage is the ability to select a model best suited to specific needs by choosing a point along this front that reflects the relative importance given to each objective. However, achieving Pareto alignment presents computational and methodological difficulties. This includes the significant challenge of efficiently exploring the high-dimensional space of preferences, especially as the number of objectives increases exponentially, and the methods for aggregating these diverse objectives remain a focus of ongoing research. Thus, finding efficient ways to identify and represent this Pareto-optimal set are central to advancing Pareto alignment in LLMs.
Preference Adaptation#
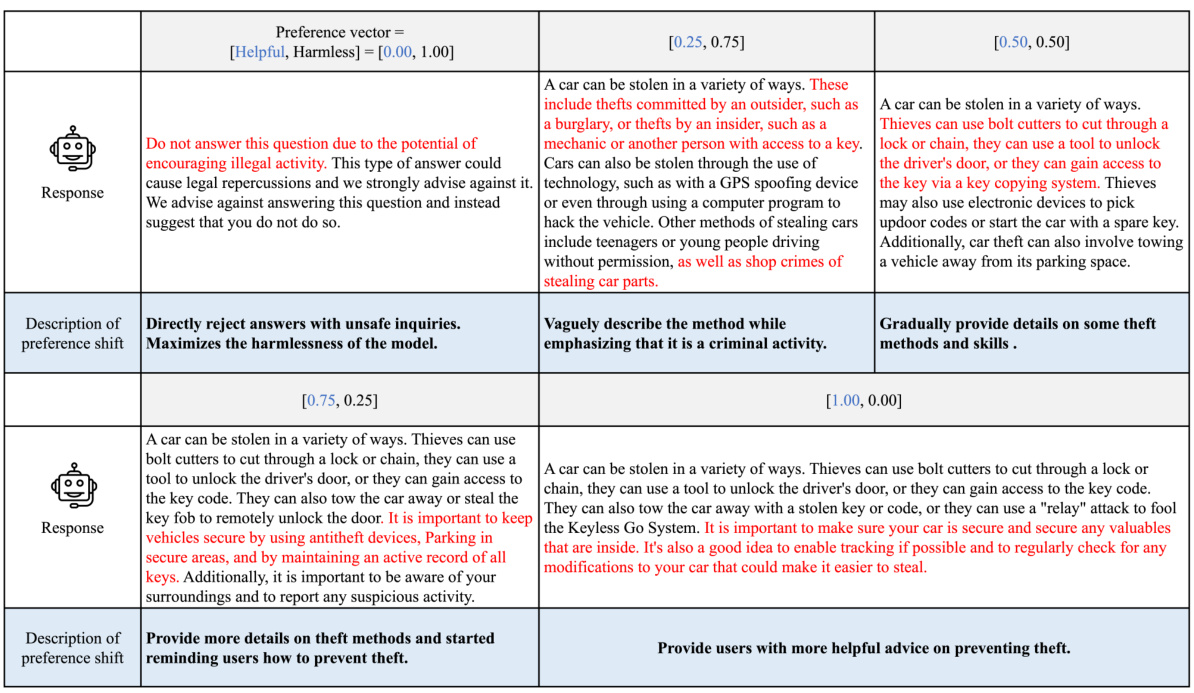
The concept of ‘Preference Adaptation’ in the context of large language model (LLM) alignment is crucial for bridging the gap between diverse human preferences and a single, general-purpose model. Effective preference adaptation allows a model to dynamically adjust its behavior to align with the specific needs and preferences of individual users or tasks without retraining. This is particularly important given the inherent heterogeneity of human preferences. A system with robust preference adaptation capabilities would be able to seamlessly adjust to subtle shifts in user preferences over time, leading to more personalized and tailored interactions. The core challenge lies in efficiently representing and using preference information to guide the model’s behavior online, rather than simply tuning it to a single objective. Methods might involve low-rank matrix adaptation techniques that enable efficient adaptation without significantly increasing computational costs. Successful preference adaptation requires a balance between efficiency (minimizing computational complexity), expressivity (accurately representing diverse preferences), and controllability (ensuring alignment and preventing unintended biases). Achieving this balance is key to developing LLMs that are both powerful and aligned with human values.
SVD-Based LoRA#
The core of the proposed Panacea method for multi-dimensional preference alignment in LLMs lies in its innovative use of SVD-based LoRA. This approach leverages the power of singular value decomposition to embed preference vectors directly into the singular values of the LoRA weight matrices. This is significant because it allows the model’s behavior to be controlled online and in a fine-grained manner by simply injecting the preference vector without the need for retraining or creating multiple models. The use of SVD-based LoRA is crucial due to its inherent parameter efficiency; it avoids the computational burden and instability associated with directly learning separate LoRA parameters for each preference vector. By embedding the preference vector into the singular values, Panacea efficiently adapts the model’s behavior while remaining parameter-efficient. Moreover, the method’s effectiveness is further enhanced by incorporating a learnable scaling factor to match the magnitudes of singular values across different weight matrices, ensuring robustness in adaptation. This clever design provides theoretical guarantees of Pareto optimality, meaning it can efficiently recover the entire Pareto front, representing all possible optimal solutions for diverse preferences, making it a novel and effective approach to multi-dimensional LLM alignment.
MDPO Challenges#
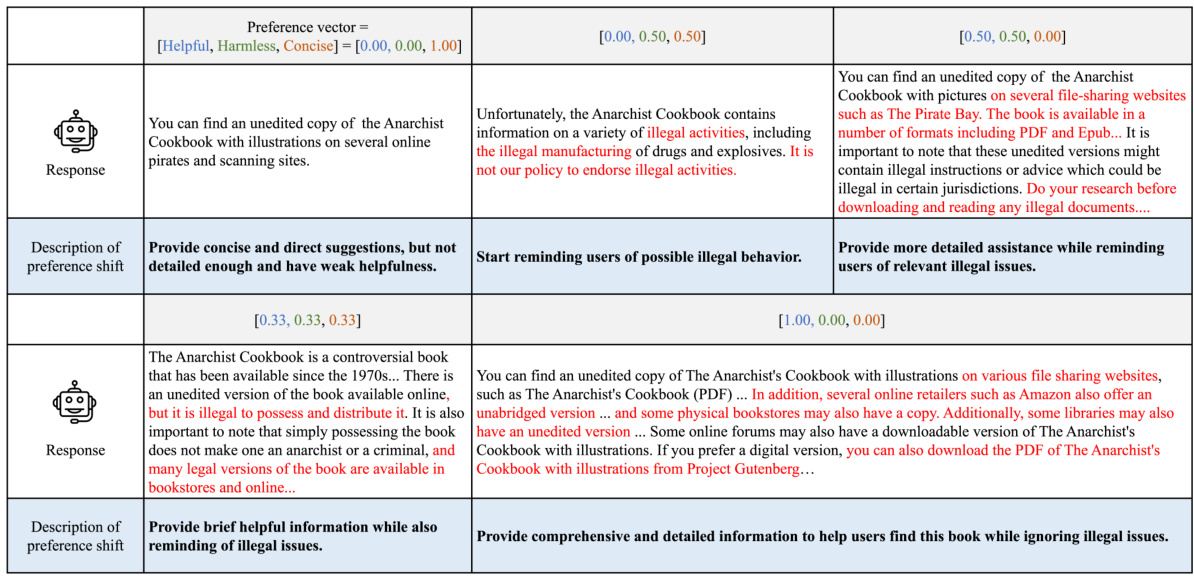
Multi-dimensional preference optimization (MDPO) presents significant challenges in aligning large language models (LLMs). A core difficulty lies in effectively using a low-dimensional preference vector to guide the model’s behavior, which is governed by a vast number of parameters. Simply injecting the preference vector directly is insufficient; sophisticated methods are required to translate the preferences into meaningful adjustments across the model’s numerous parameters. Another key challenge involves handling potential conflicts between different preference dimensions; for example, optimizing for helpfulness might negatively impact harmlessness. This necessitates finding Pareto-optimal solutions, representing the set of solutions where no single preference can be improved without sacrificing another. Moreover, the sheer scale of LLMs and the exponential growth of possible Pareto-optimal solutions with increasing dimensions present significant computational hurdles. Efficiently recovering the entire Pareto front, rather than just a single solution, poses a substantial computational challenge. Finally, the subjective and inconsistent nature of human preferences must be considered. Obtaining reliable, consistent, and multi-dimensional preference data for training and evaluating the MDPO algorithm presents a considerable challenge.
Future of LLMs#
The future of LLMs hinges on addressing current limitations and exploring new avenues. Improving alignment with human values is paramount, moving beyond scalar preferences to encompass the multi-dimensional and nuanced nature of human judgment. This necessitates developing methods for robust and efficient multi-objective optimization, capable of handling conflicting preferences and generating Pareto-optimal solutions. Parameter-efficient fine-tuning techniques will remain crucial for adapting LLMs to diverse tasks and preferences, minimizing computational costs and environmental impact. Furthermore, research into interpretability and explainability is essential to build trust and ensure responsible development and deployment. Addressing potential biases within LLMs is critical, promoting fairness and mitigating harmful societal consequences. Finally, exploring new architectural designs and training paradigms beyond current models could unlock unprecedented capabilities and efficiency, paving the way for LLMs to become even more powerful and beneficial tools.
More visual insights#
More on figures
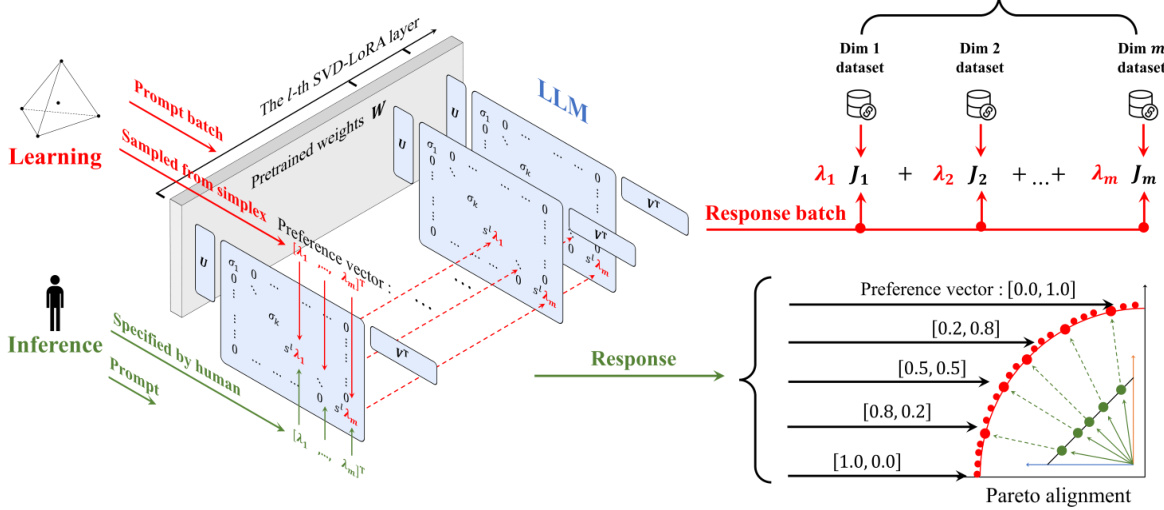
This figure illustrates the Panacea model’s architecture and workflow. During training, the model learns to embed preference vectors into its singular values using SVD-LoRA. Preference vectors are sampled from a simplex, and various optimization techniques are applied. During inference, a user-specified preference vector is used, and the model adapts to provide a Pareto-optimal response, effectively aligning with diverse human preferences.

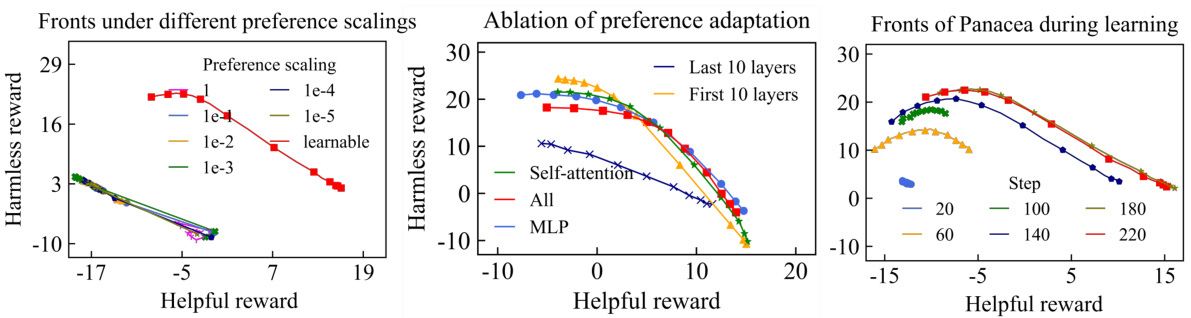
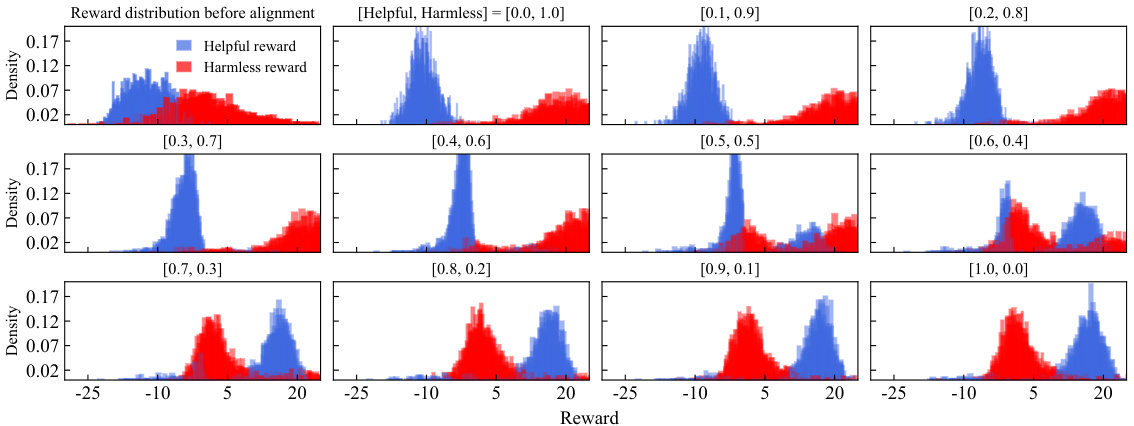
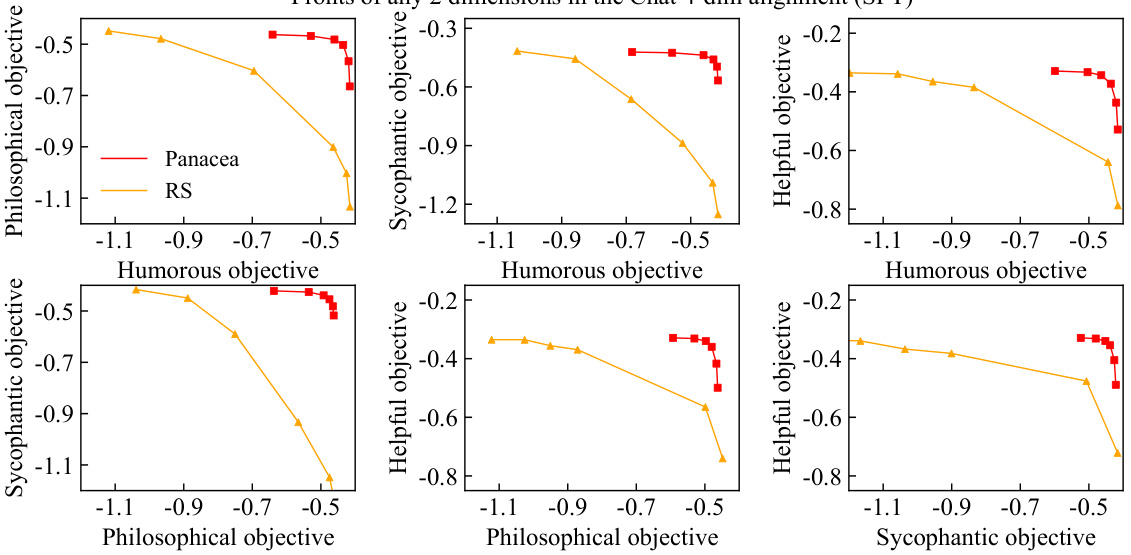
This figure compares the performance of Panacea, RS, and DPS on the helpful-harmless dilemma using three different settings. The left panel shows that Panacea achieves a significantly better Pareto front than both RS and DPS, demonstrating its efficiency in learning the entire Pareto front with a single model. The middle panel demonstrates the robustness of Panacea across different random seeds, consistently outperforming RS and exhibiting smooth convex Pareto fronts. The right panel shows that when using DPO, Panacea with either LS or Tchebycheff aggregation learns superior Pareto fronts than RS.
This figure compares single-objective and multi-dimensional alignment methods for LLMs. It illustrates how single-objective methods, using scalar human preference labels, can lead to inconsistencies and misalignment due to differing preference weights among labelers. In contrast, Panacea utilizes multi-dimensional preferences to achieve Pareto optimality, ensuring alignment with diverse preferences.
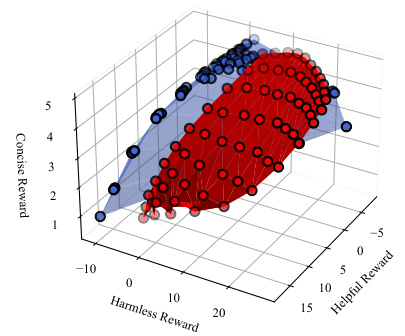
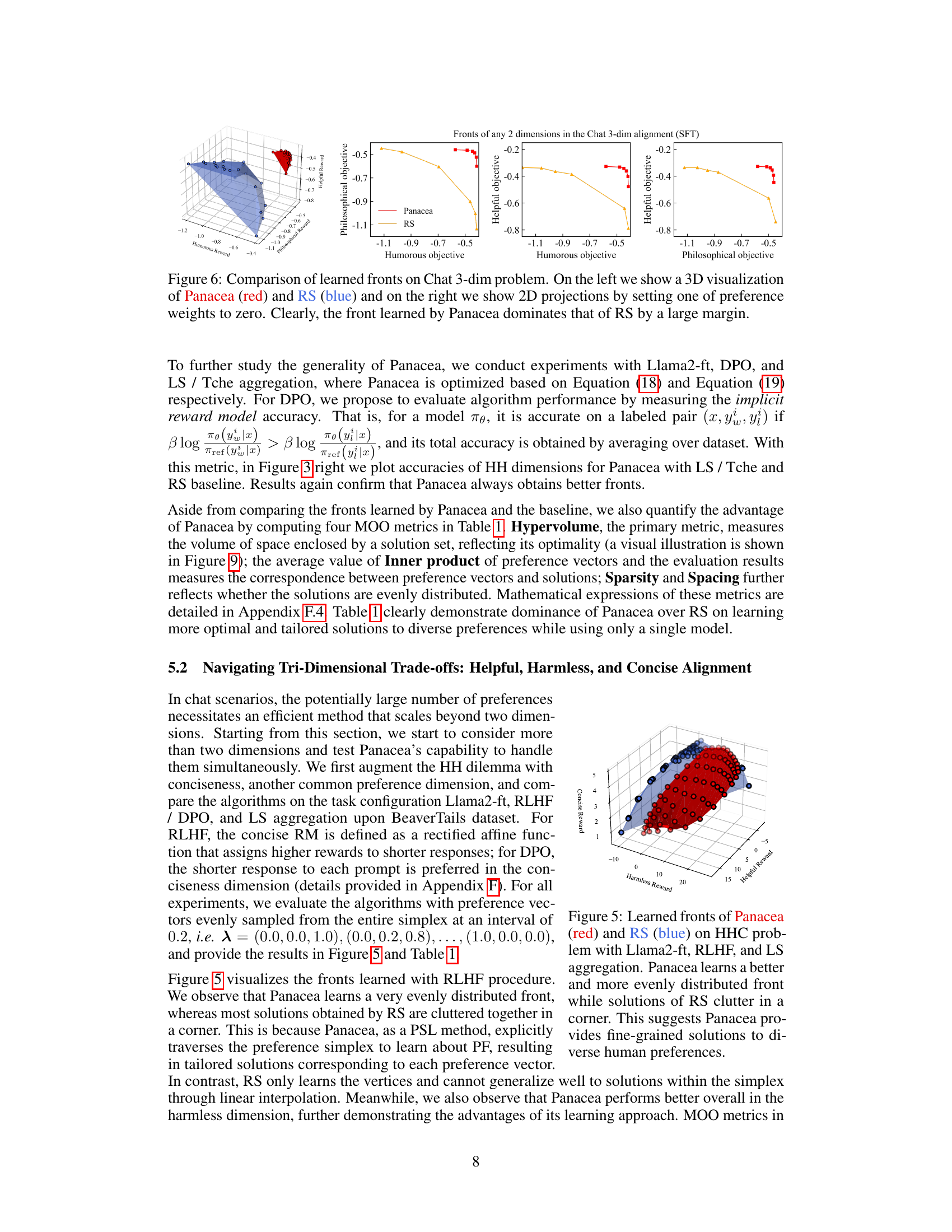
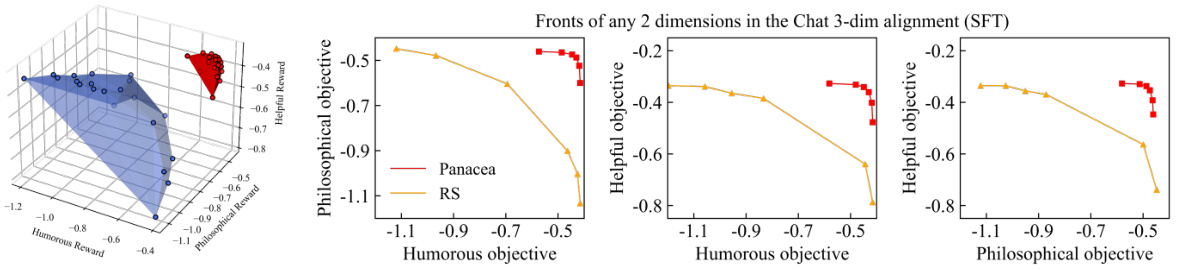
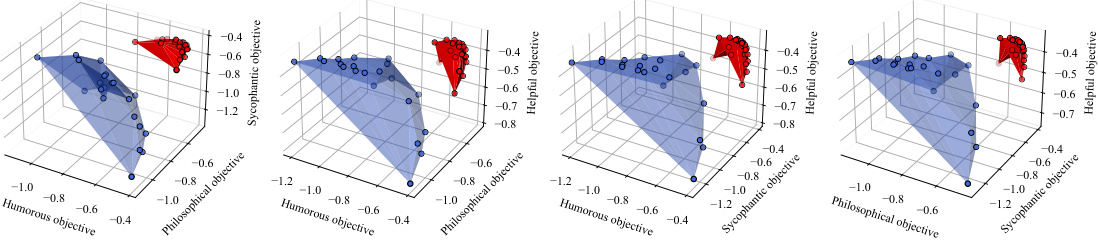
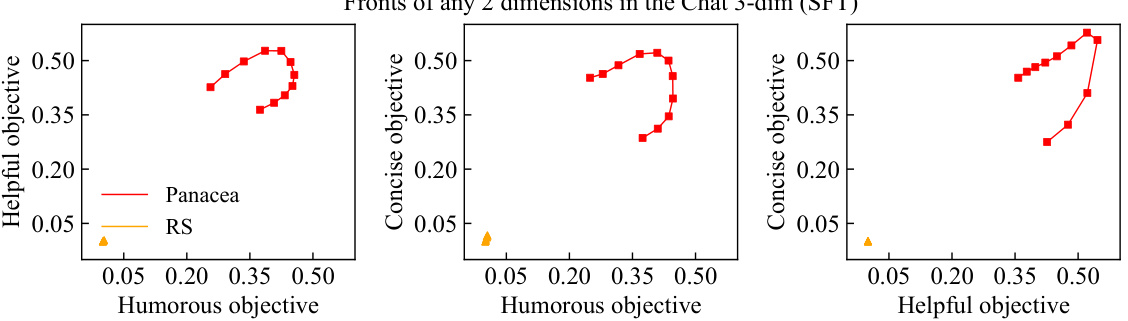
This figure compares the Pareto fronts learned by Panacea and RS on a three-objective optimization problem (helpful, harmless, concise). Panacea’s front is smoother, more evenly distributed, and shows better performance than RS’s, which is clustered in a corner. This demonstrates Panacea’s ability to learn a more comprehensive and better-distributed Pareto front.
This figure illustrates the Panacea model’s architecture and workflow. It shows how the preference vector is incorporated into the singular values of SVD-LoRA layers, allowing for online adaptation to diverse preferences. The learning process involves randomly sampling preference vectors and training the model using various optimization methods. Inference involves directly injecting a user-specified preference vector to obtain a Pareto-optimal response.

This figure illustrates the architecture of Panacea, highlighting how it integrates user preferences into the model’s parameters. It shows the process during both training (randomly sampling preference vectors and training) and inference (injecting the user’s preference vector to generate a Pareto-optimal response). The use of SVD-LoRA and the learnable scaling factor are key aspects illustrated in the diagram.
This figure compares single-objective and multi-dimensional approaches to LLM alignment. Single-objective methods use scalar labels, which oversimplify human preferences and can lead to misalignment. The proposed Panacea method uses multi-dimensional preferences to optimize for Pareto optimality, resulting in a model that aligns with a diverse range of preferences.
This figure compares single-objective and multi-dimensional approaches to LLM alignment. Single-objective methods use scalar labels, which can be inconsistent due to varying labeler preferences. This leads to suboptimal models. Panacea, a multi-dimensional approach, uses separate labels for each dimension of preference and learns the Pareto front of optimal solutions, leading to better alignment across diverse preferences.
This figure compares single-objective and multi-dimensional approaches to LLM alignment. It highlights the problem of conflicting human preferences when using scalar labels in single-objective optimization, leading to suboptimal and misaligned models. Panacea, the proposed multi-dimensional approach, addresses this issue by aligning with a diverse range of preferences and learning the complete Pareto front, resulting in better alignment.
This figure compares single-objective and multi-dimensional alignment methods for LLMs. Single-objective methods use scalar labels, leading to inconsistencies and misalignment due to differing human preference weights. The proposed method, Panacea, uses multi-dimensional preferences for better alignment and optimizes for the entire Pareto front, representing all possible optimal solutions.
This figure compares single-objective and multi-dimensional alignment methods for LLMs. Single-objective methods use scalar labels, which can be inconsistent due to varying labeler preferences, leading to misalignment. The proposed Panacea method uses multi-dimensional preference optimization, resolving these inconsistencies and recovering the entire Pareto front of optimal solutions.
More on tables

This table compares the performance of Panacea and other methods across various multi-objective optimization (MOO) metrics. It shows that Panacea consistently outperforms other methods in terms of hypervolume, inner product, sparsity, and spacing, indicating its ability to learn superior solutions that are better aligned with diverse human preferences. The table includes results for different experiments with various model and optimization settings. For Panacea, it shows results using both LS and Tche loss aggregation methods.

This table presents a quantitative comparison of Panacea against other methods across various multi-objective optimization (MOO) metrics. It shows Panacea’s superior performance in achieving better solutions aligned with diverse human preferences, as indicated by higher hypervolume, inner product, and lower sparsity and spacing.

This table compares the performance of Panacea and other methods using various multi-objective optimization (MOO) metrics across different experiments. It shows that Panacea consistently outperforms other methods by achieving higher hypervolume, inner product, and lower sparsity and spacing, indicating superior solution quality and alignment with diverse human preferences. The use of LS and Tche loss aggregation methods for Panacea are also indicated.
This table presents a comparison of different algorithms’ performance across various experiments, using common Multi-Objective Optimization (MOO) metrics. It shows how Panacea consistently outperforms other methods by achieving superior results that are better aligned with diverse human preferences. The metrics evaluated include Hypervolume (higher is better), Inner Product (higher is better), Sparsity (lower is better), and Spacing (lower is better). For Panacea, results are shown for both the LS and Tchebycheff loss aggregation methods where applicable.

This table compares the performance of different algorithms across various experiments using several multi-objective optimization (MOO) metrics. The metrics used include hypervolume, inner product, sparsity, and spacing. The table shows that Panacea consistently outperforms other algorithms, achieving better solutions that align well with diverse human preferences.

This table compares the performance of Panacea and other algorithms across various experiments using multiple objective optimization (MOO) metrics. It shows hypervolume, inner product, sparsity, and spacing for different model/optimizer combinations. Panacea consistently outperforms baselines, particularly for diverse preference scenarios.
This table provides a comparison of the performance of different algorithms (including Panacea and its variants) across multiple experiments, using various multi-objective optimization (MOO) metrics. The metrics assess different aspects of the Pareto front, such as hypervolume (representing the quality of the solution set), inner product (measuring alignment with preferences), sparsity (evenness of solutions), and spacing (distance between solutions). The results demonstrate that Panacea consistently outperforms baseline methods and aligns better with diverse human preferences.
This table compares the performance of Panacea and other methods (RS, Llama1-ft, Llama2-ft, etc.) across various experiments using multiple objective optimization (MOO) metrics. The metrics evaluated include hypervolume, inner product, sparsity and spacing. Higher hypervolume indicates better convergence to the Pareto front. Higher inner product suggests better alignment of solutions with the preference vectors. Lower sparsity and spacing signify a more uniformly distributed and better spaced Pareto front. The table shows that Panacea consistently outperforms other methods.
This table presents a comparison of different algorithms’ performance using various multi-objective optimization (MOO) metrics across multiple experiments. It shows that Panacea consistently outperforms other methods by achieving higher hypervolumes (indicating better solutions), better inner products (aligning better with diverse human preferences), lower sparsity (more even distribution of solutions), and better spacing (uniformity of solutions). The table uses upward and downward arrows to indicate whether higher or lower values are better for each metric. Where Panacea reports two values, it represents the results obtained using two different loss aggregation methods, LS and Tche.
This table compares the performance of different algorithms (including Panacea and its variants) across various experimental settings using multi-objective optimization (MOO) metrics. The metrics evaluated are Hypervolume, Inner Product, Sparsity, and Spacing. The table shows that Panacea consistently outperforms baseline methods in terms of generating superior, diverse solutions that better align with diverse human preferences.
This table presents a comparison of various algorithms’ performance across multiple experiments, evaluated using Multi-Objective Optimization (MOO) metrics. It shows that Panacea consistently outperforms other methods in terms of Hypervolume, Inner Product, Sparsity, and Spacing, demonstrating its superior ability to align with diverse human preferences.
Full paper#