↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Interpreting complex machine learning models is a significant challenge. Existing methods, like Shapley values, often struggle to capture higher-order interactions between inputs, limiting their explanatory power. Moreover, computing these measures can be computationally expensive, hindering their applicability to large models. This research addresses this challenge by focusing on the Möbius transform, a powerful mathematical tool that directly represents the importance of input sets.
The proposed algorithm significantly reduces the computational cost of computing the Möbius transform by exploiting sparsity and low-degree properties often observed in real-world models. It uses advanced group-testing techniques, leading to a non-adaptive algorithm with sub-linear sample complexity and robustness to noise. This is a major advancement because it allows efficient model interpretation even for large datasets and noisy environments. The study also provides rigorous theoretical guarantees and supports these claims with extensive simulations on real-world and synthetic datasets, demonstrating superior accuracy and efficiency compared to standard approaches.
Key Takeaways#
Why does it matter?#
This paper offers a novel, efficient algorithm for understanding complex machine learning models by identifying interactions between inputs. It is significant due to its non-adaptive, noise-tolerant nature and sub-linear query complexity, solving a crucial challenge in model interpretability.
Visual Insights#

This figure shows how the Möbius transform can provide a more nuanced understanding of sentiment analysis compared to simpler methods like Shapley values. It uses a BERT model analyzing the sentence ‘Her acting never fails to impress.’ The Möbius coefficients, visualized by color-coded values, show the interaction effects of different word combinations on the overall sentiment. Note that the removal of the word ’never’ significantly alters the sentiment, highlighting the importance of higher-order interactions that Shapley values alone cannot capture.

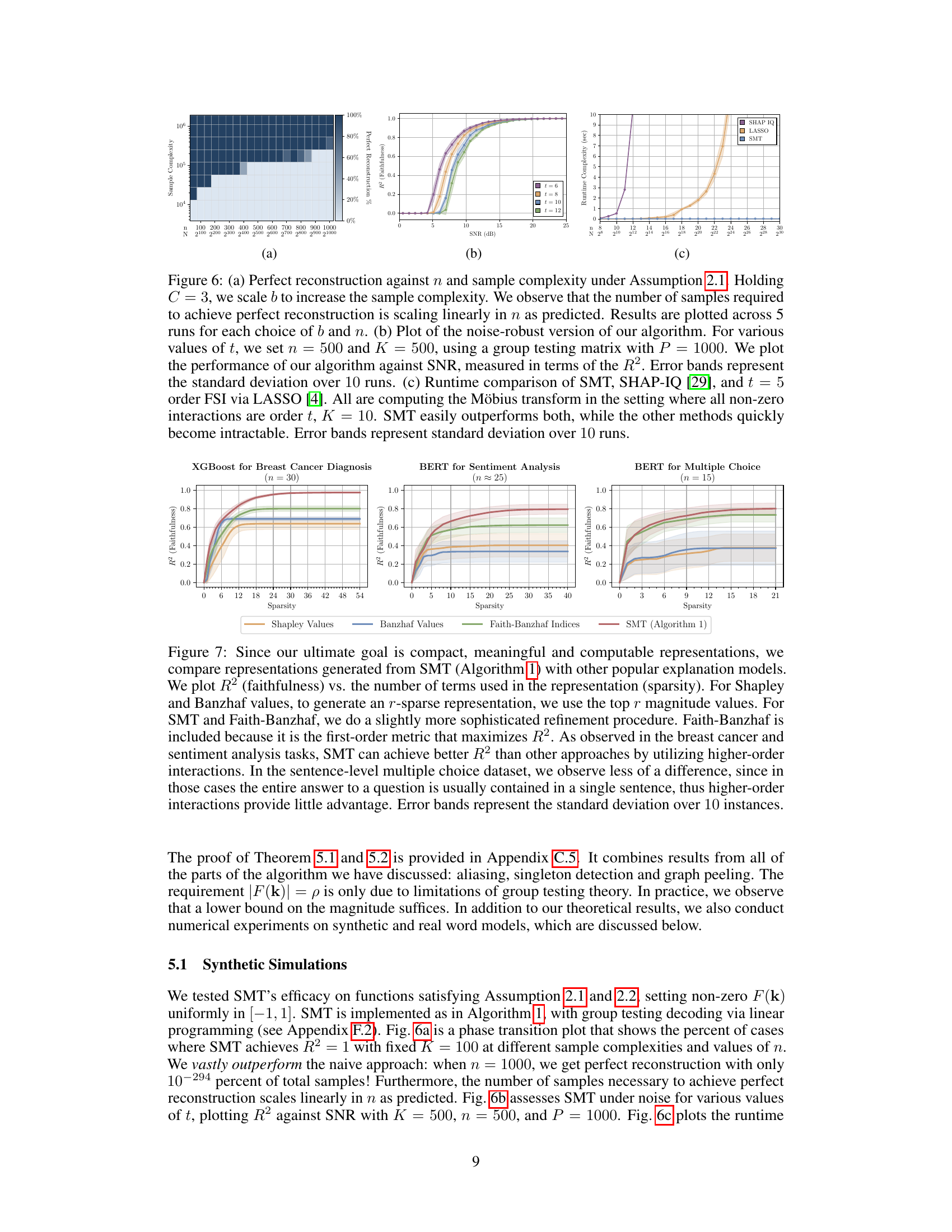
This table shows an example of how group testing can be used to efficiently identify singletons (Möbius coefficients with only one non-zero interaction). The first row represents a sentence with several words. Each row in the matrix Dc shows a subset of the words that are masked (value 0) and unmasked (value 1). The final column shows the output of the model based on which words were masked in that row. By cleverly designing the masking patterns using group testing techniques, it is possible to quickly identify which word (in this case, “never”) corresponds to the singleton in the Möbius transform, even with high-dimensional input. This approach significantly reduces the computational complexity of identifying non-zero interactions by utilizing group testing for efficient sparse Möbius transform computation.
In-depth insights#
Sparse Möbius#
The concept of “Sparse Möbius” in a machine learning context refers to a computationally efficient approach to using the Möbius transform for interpreting complex models. The Möbius transform is powerful for identifying and quantifying interactions between input variables, providing an interpretable representation of the model’s behavior. However, a standard Möbius transform has an exponential complexity (2n coefficients for n inputs), making it intractable for high-dimensional data. The “Sparse” aspect addresses this limitation by assuming the model’s output is primarily determined by a relatively small number of non-zero Möbius coefficients. This sparsity assumption, often observed in real-world models, greatly reduces computational complexity. Algorithms exploiting sparsity can significantly reduce both the sample complexity (number of model evaluations) and runtime needed to recover these important interactions, making the approach practically feasible for higher-dimensional data. This allows researchers to gain valuable insights into complex models without incurring the computational costs of a full Möbius transform. The use of group testing techniques can further enhance efficiency and robustness to noise in the data, furthering the practicality of the Sparse Möbius method. In essence, Sparse Möbius offers a balance between interpretability and computational efficiency for understanding and explaining machine learning models.
Group Testing#
The concept of ‘Group Testing’ in the context of the research paper presents a novel and efficient approach to identifying significant interactions within complex systems. It leverages the principles of group testing, originally developed for medical screening, to significantly reduce the number of samples needed to compute the Möbius transform. This is particularly crucial when dealing with high-dimensional data, where exhaustive testing becomes computationally intractable. The integration of group testing demonstrates a surprising connection between this established field and the computation of the Möbius transform. The algorithm’s efficiency stems from its non-adaptive nature, allowing for parallelization and further improving its speed and scalability. This approach significantly lowers both the sample and time complexity, rendering the computation of the Möbius transform feasible for previously unapproachable data sizes. The effectiveness of the method is highlighted through theoretical analysis and real-world experiments, showcasing its power for uncovering interpretable representations of complex models.
SMT Algorithm#
The Sparse Möbius Transform (SMT) algorithm is a computationally efficient method for identifying interactions within complex systems, particularly useful in machine learning model explainability. Its core innovation lies in leveraging sparsity and low-degree assumptions of real-world functions. By cleverly employing techniques from group testing and signal processing, SMT significantly reduces the number of queries needed to compute the Möbius transform, making it tractable for high-dimensional data. The algorithm’s robustness to noise is another strength, enhancing its applicability to real-world scenarios where perfect data is rarely available. The connection between group testing and the Möbius transform itself is a key theoretical contribution. This is important because group testing is well-studied, offering both theoretical guarantees and readily available efficient algorithms. Ultimately, SMT provides a powerful tool for uncovering crucial insights into the workings of complex models, paving the way for more interpretable and trustworthy AI systems. Its sub-linear query complexity and noise tolerance mark significant advances over previous approaches.
Interpretability#
The concept of interpretability in machine learning is explored, focusing on the challenges of understanding complex models. The Möbius transform is highlighted as a crucial tool for achieving interpretability, offering unique importance scores for sets of input variables and capturing higher-order interactions that other methods, like Shapley values, often miss. The paper addresses the computational complexity of calculating the Möbius transform by leveraging sparsity and low-degree assumptions common in real-world functions. A novel algorithm (SMT) is proposed, combining subsampling techniques with group testing principles to significantly reduce the computational cost while maintaining accuracy, even in the presence of noise. The effectiveness of the SMT algorithm is validated through theoretical analysis and real-world experiments, demonstrating the generation of more faithful model representations compared to existing methods. Key contributions include non-adaptive algorithms with sub-linear query complexities and robustness to noise, ultimately advancing the field of interpretable machine learning.
Future works#
The “Future Works” section of a research paper on the M
“obius Transform for interaction identification would ideally outline several promising avenues for future research. Extending the algorithm’s applicability to non-sparse, high-degree functions is a crucial direction. The current work assumes sparsity and low degree; relaxing these assumptions would significantly broaden its practical impact. Further research should explore robustness to various noise models, beyond the additive Gaussian noise considered. Real-world data often exhibits more complex noise patterns. Investigating the computational efficiency is vital, especially for large-scale applications involving many inputs. While the current algorithm shows sub-linear complexity under specific conditions, improved efficiency is needed. Another critical area is developing theoretical guarantees for the finite-sample regime, moving beyond asymptotic analysis. Finally, applying the Möbius Transform to different domains such as natural language processing, computer vision, or time-series analysis would greatly expand the method’s reach and impact. The development of novel applications based on the improved explanation capacity of the Möbius transform over Shapley values should also be prioritized.
More visual insights#
More on figures

This figure empirically validates the sparsity and low-degree assumptions of the proposed algorithm. It shows the faithfulness (R-squared) of the Möbius transform approximations for three different machine learning tasks (breast cancer diagnosis, sentiment analysis, and multiple choice) as a function of sparsity and degree. The plots demonstrate that a small number of coefficients (low sparsity and low degree) are sufficient to achieve high faithfulness, supporting the algorithm’s assumptions.
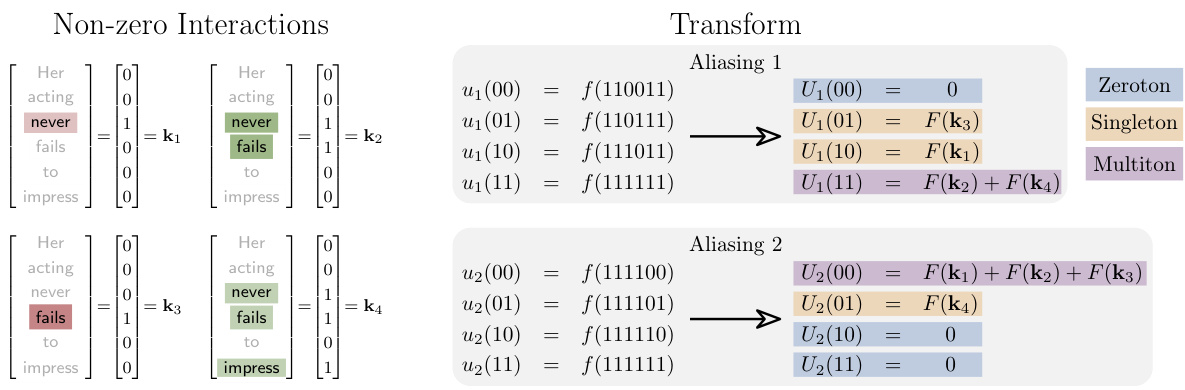
This figure illustrates the concept of aliasing in the context of the Möbius transform. It shows how different subsampling strategies (Aliasing 1 and Aliasing 2) can lead to different groupings of the non-zero Möbius coefficients. These groupings are categorized as zerotons (all zero coefficients), singletons (only one non-zero coefficient), and multitons (more than one non-zero coefficient). The figure highlights that the effectiveness of the sparse Möbius transform algorithm depends on maximizing the number of singletons.

This figure shows two different ways of subsampling the Möbius transform to reduce the computational complexity. Each subsampling method results in a different aliasing structure, shown as a bipartite graph with variable nodes (non-zero Möbius coefficients) and check nodes (subsampled function values). The different aliasing patterns highlight the impact of subsampling choices on the number of singletons (easily recovered coefficients) and multitons (coefficients that require further processing).
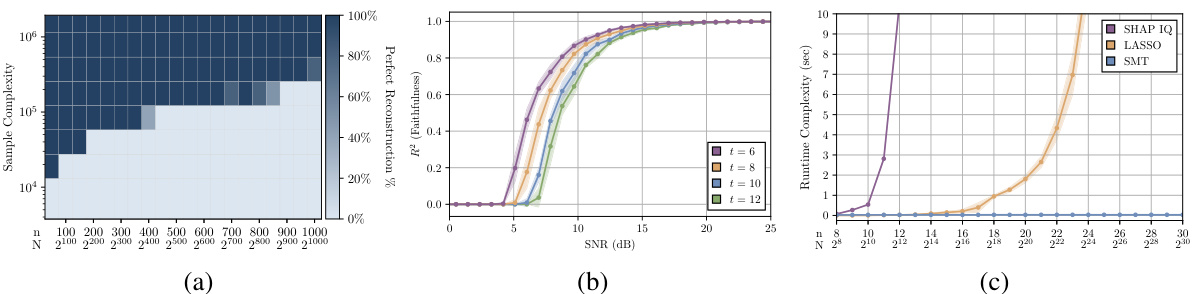
This figure demonstrates the performance of the Sparse Möbius Transform (SMT) algorithm under different conditions. Subfigure (a) shows the perfect reconstruction percentage against the sample complexity and n under Assumption 2.1. Subfigure (b) shows the performance of the noise-robust version of the SMT algorithm for various t, n, K, and P. Subfigure (c) compares the runtime complexity of SMT, SHAP-IQ, and FSI via LASSO.

This figure compares the faithfulness (R²) of different explanation models (SMT, Shapley values, Banzhaf values, Faith-Banzhaf indices) against the sparsity (number of terms used in the representation) for three real-world machine learning tasks. SMT consistently achieves higher faithfulness with the same or fewer terms compared to other methods, highlighting its ability to leverage higher-order interactions for better model interpretability.
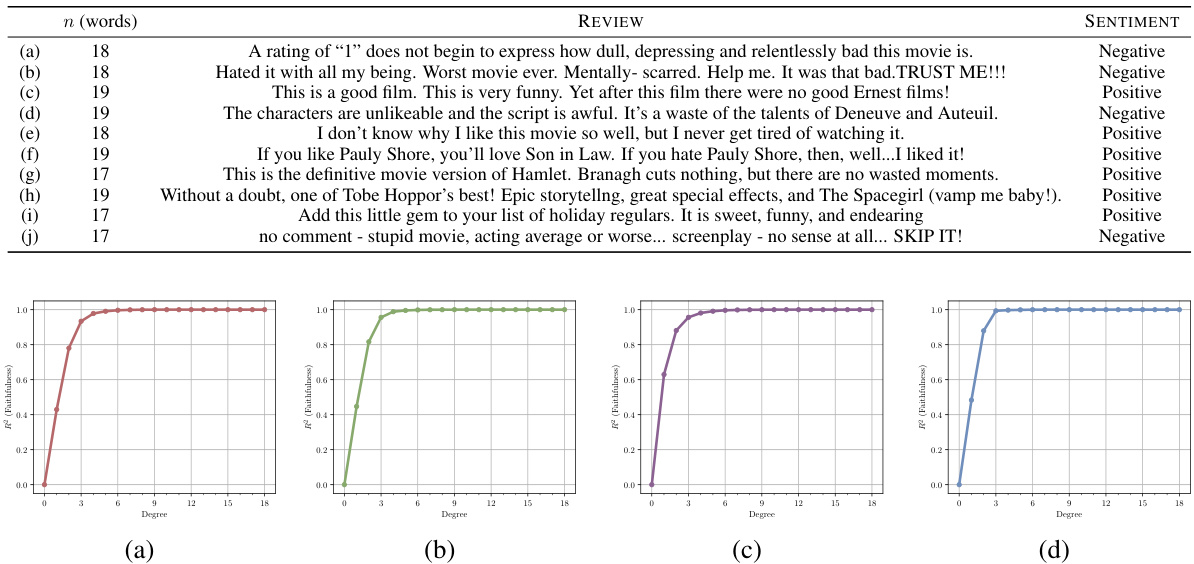
This figure shows plots that support the assumptions of sparsity and low degree for real-world functions. Three different machine learning tasks (breast cancer diagnosis, sentiment analysis, and multiple choice) are examined. The top row shows how much of the function’s behavior can be explained using a certain number of non-zero Möbius coefficients (sparsity). The bottom row shows how much can be explained by considering only interactions of a certain degree. In all cases, a relatively small number of coefficients suffices for high R-squared (faithfulness), which suggests sparsity and low degree are reasonable.

This figure empirically validates the assumptions of sparsity and low degree of the Möbius transform for real-world machine learning models. It shows that for three different tasks (breast cancer diagnosis, sentiment analysis, and multiple choice question answering), a small number of Möbius coefficients are sufficient to achieve high faithfulness (R^2). The plots depict R^2 as a function of sparsity and degree of the transform.

This figure shows the symmetric cross-over probability in a hypothesis testing problem for noisy singleton identification and detection. The x-axis represents the signal-to-noise ratio (ρ/σ), and the y-axis represents the crossover probability. The curve shows how the probability of making a correct decision changes with the signal-to-noise ratio.
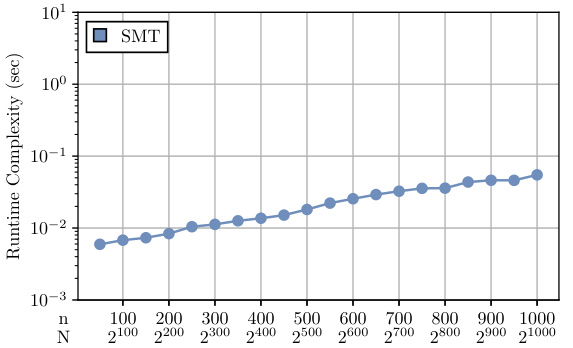
This figure demonstrates the performance of the Sparse Möbius Transform (SMT) algorithm under different conditions. Subfigure (a) shows the perfect reconstruction percentage against the number of samples under Assumption 2.1, demonstrating a linear scaling. Subfigure (b) illustrates the algorithm’s noise robustness under various interaction orders (t), showcasing the R² (faithfulness) against the signal-to-noise ratio (SNR). Lastly, subfigure (c) compares the runtime complexity of SMT against other approaches like SHAP-IQ and LASSO for computing the Möbius transform, clearly showing SMT’s superiority.
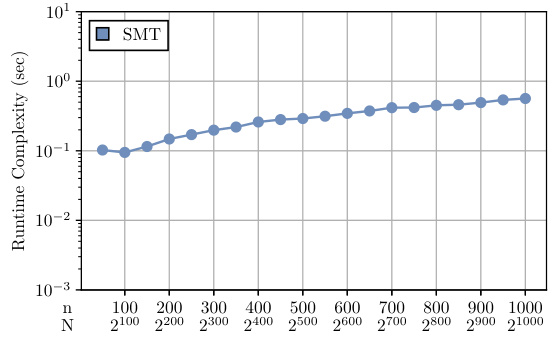
This figure shows the results of experiments to evaluate the performance of the Sparse Möbius Transform (SMT) algorithm. Panel (a) demonstrates the linear scaling of sample complexity with the number of features (n) under perfect reconstruction conditions. Panel (b) illustrates the algorithm’s robustness to noise, showing faithfulness (R²) against signal-to-noise ratio (SNR) for different interaction orders. Panel (c) compares the runtime of SMT to other methods (SHAP-IQ and LASSO), highlighting SMT’s superior efficiency.

This figure demonstrates the performance of the Sparse Möbius Transform (SMT) algorithm under different conditions. (a) shows the perfect reconstruction percentage against the number of samples and n under Assumption 2.1. (b) shows the performance of the noise-robust version of the algorithm against signal-to-noise ratio (SNR) under Assumption 2.2 with different maximum interaction orders (t). (c) compares the runtime of SMT with other methods (SHAP-IQ and LASSO) for computing the Möbius transform with a fixed number of non-zero interactions (K).
More on tables

This table shows the addition, multiplication, and subtraction operations for boolean arithmetic used in the paper. Note that the subtraction is only defined when y ≤ x.

This table defines the addition, multiplication, and subtraction operations in the Boolean arithmetic used in the paper. Note that the subtraction operation is only defined when y ≤ x. The table clarifies how these operations are performed in the context of the paper’s mathematical framework, which is relevant to the interpretation of the Möbius transform and interaction indices.
Full paper#