TL;DR#
Evaluating the diversity of latent representations in deep learning models is crucial but challenging. Existing methods often lack the expressivity to capture the complexities of high-dimensional data and struggle with the stability issue. This research proposes a new family of diversity measures based on the mathematical concept of “metric space magnitude.” Magnitude, a multi-scale summary of the space’s geometry, effectively handles the aforementioned issues.
The proposed measures are shown to be stable under data perturbations, computationally efficient, and effective in various domains. Their utility is demonstrated through improved performance in automated diversity estimation, mode collapse detection in generative models, and embedding model characterization across text, image, and graph data. This work provides a principled, mathematically grounded approach to evaluating latent space diversity.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel, robust method for evaluating the diversity of latent representations in machine learning models. It addresses a critical need for reference-free diversity measures that can capture multi-scale geometric properties. This method has the potential to improve model evaluation and selection across various domains. The rigorous theoretical foundation and demonstrated effectiveness make it a significant contribution to the field.
Visual Insights#

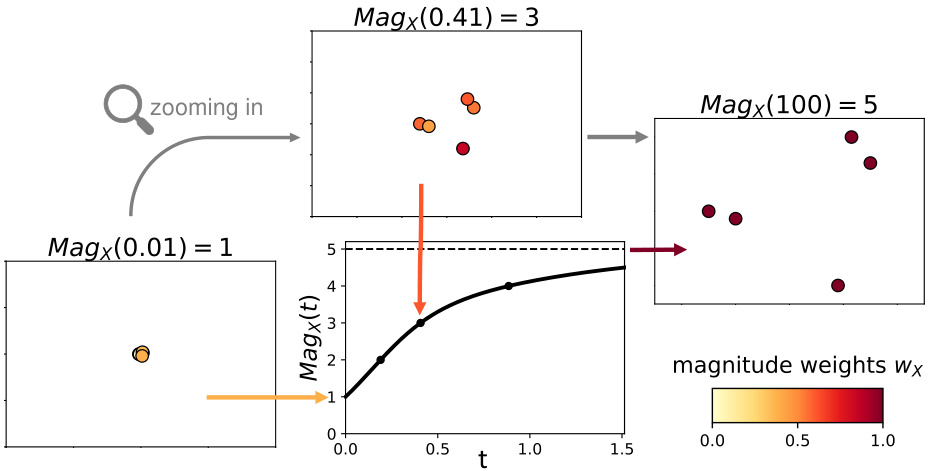
🔼 This figure provides a visual overview of the proposed diversity evaluation pipeline using metric space magnitude. It showcases how the magnitude function captures the effective number of points in a latent space at various scales. The pipeline uses the area under the magnitude curve (MAGAREA) for reference-free diversity and the difference between magnitude curves (MAGDIFF) for reference-based diversity comparisons. The figure illustrates these concepts with example latent spaces and their corresponding magnitude functions.
read the caption
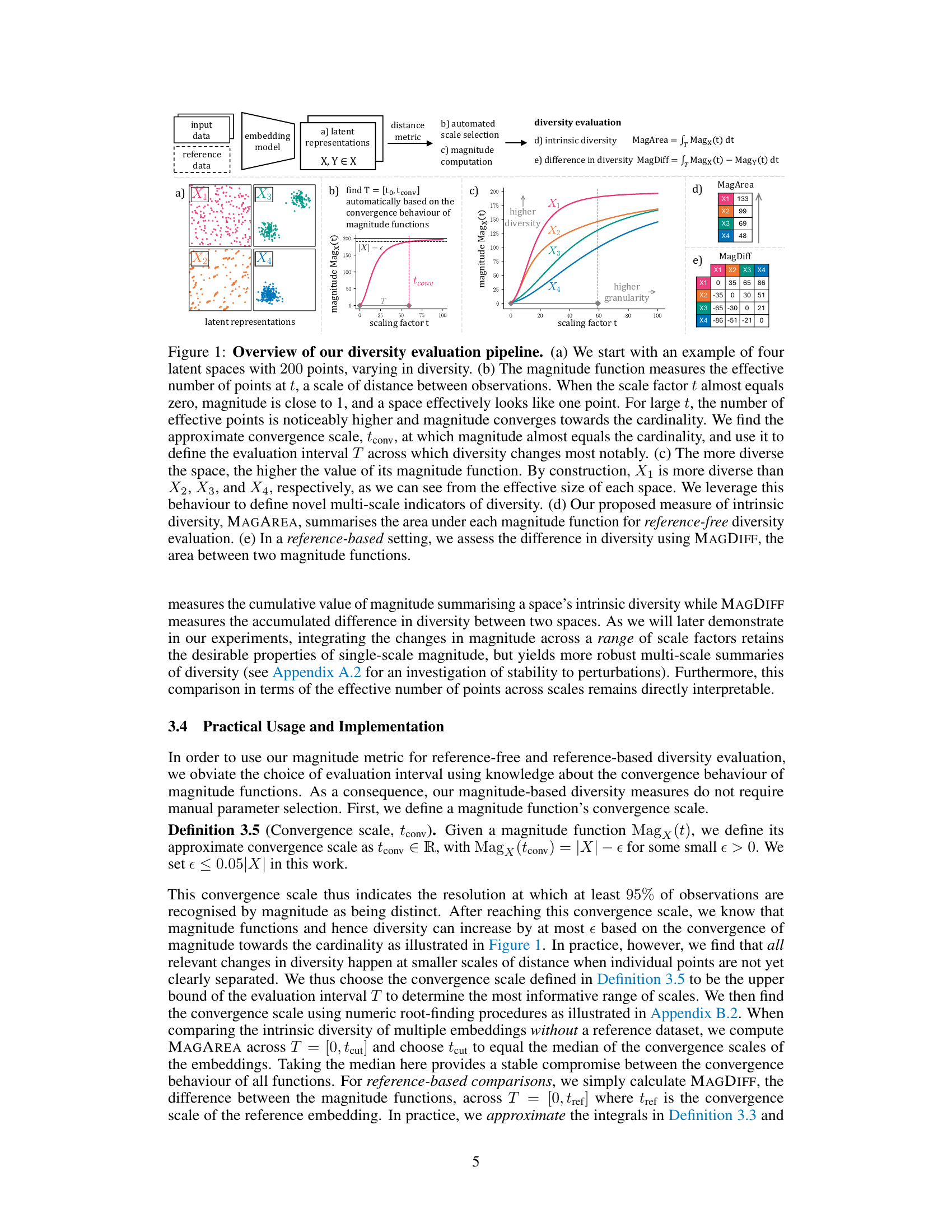
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.
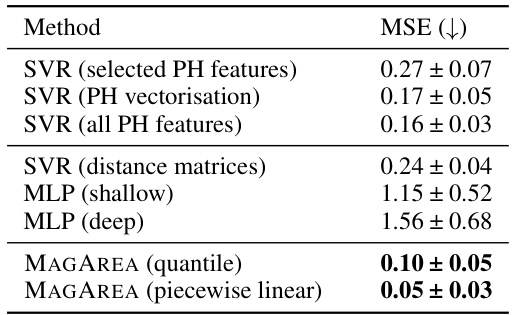
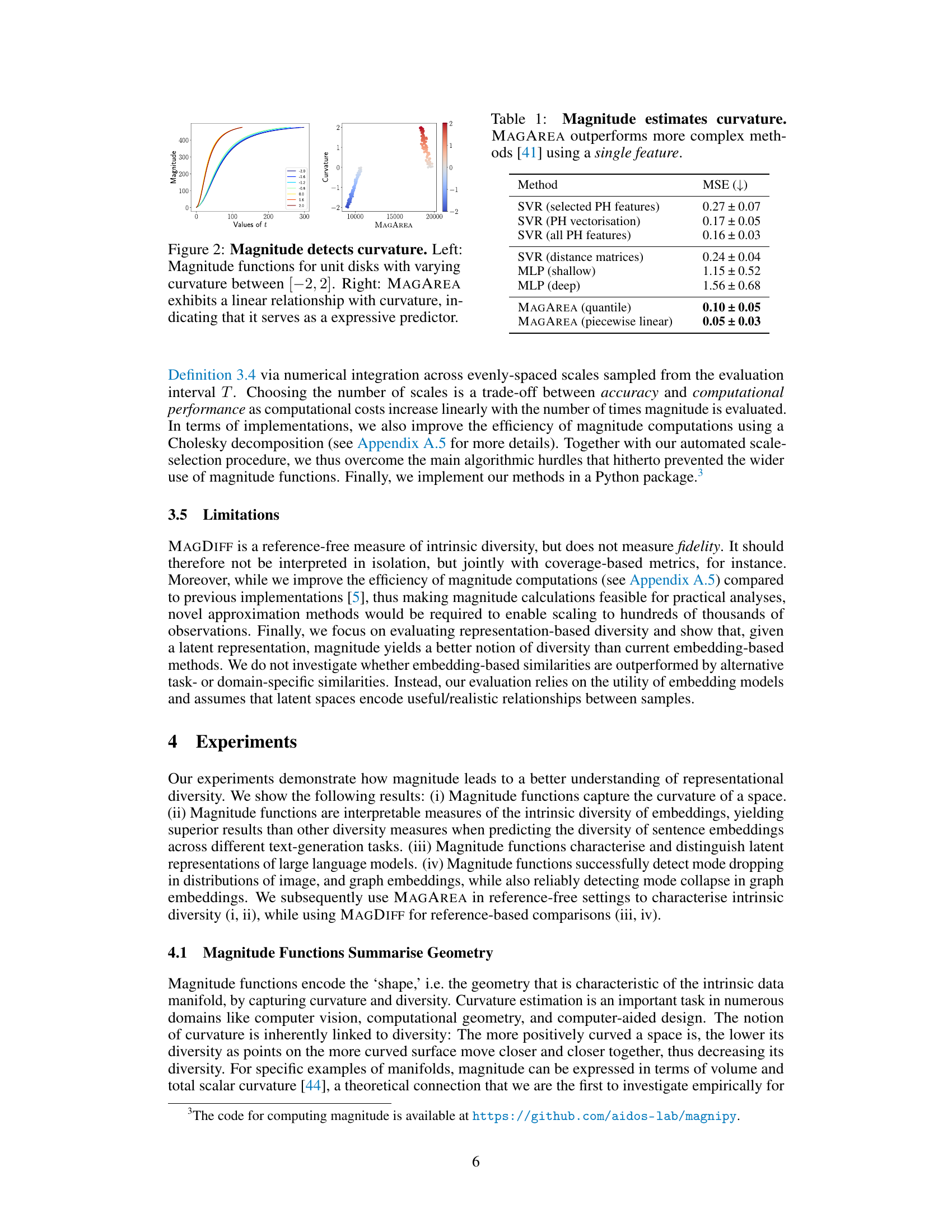
🔼 This table compares the mean squared error (MSE) of different methods for estimating curvature. The methods include Support Vector Regression (SVR) using various features derived from persistent homology (PH) analysis, Multilayer Perceptrons (MLP) with shallow and deep architectures, and the proposed MAGAREA method using both quantile and piecewise linear regression. The results show that MAGAREA achieves the lowest MSE, indicating its superior performance in curvature estimation, especially when compared to more complex methods.
read the caption
Table 1: Magnitude estimates curvature. MAGAREA outperforms more complex methods [41] using a single feature.
In-depth insights#
Metric Space Mag.#
The concept of “Metric Space Magnitude” offers a novel, multi-scale approach to evaluating the diversity of latent representations in machine learning. It moves beyond single-scale metrics by capturing the ’effective size’ of a data space across multiple levels of similarity. This is valuable because it provides a more holistic understanding of diversity, incorporating both local and global geometric characteristics, which are often missed by traditional measures. Its multi-scale nature allows for a more nuanced understanding of the distribution of data points. The framework’s strength lies in its theoretical foundation, satisfying key desiderata for diversity measures and offering proven stability under data perturbations. Unlike entropy-based methods, it directly incorporates geometric properties of the data space. Its broad applicability across domains, from text and images to graphs, is a considerable strength. However, computational costs remain a consideration for very large datasets and further investigation is needed to optimize computational efficiency for larger-scale applications. The framework shows considerable promise in addressing the need for robust and interpretable diversity assessments in machine learning.
Multi-scale Diversity#
The concept of “Multi-scale Diversity” proposes a nuanced perspective on data diversity, moving beyond simplistic single-scale metrics. It acknowledges that datasets exhibit variations in their diversity at different levels of granularity. Analyzing diversity across multiple scales is crucial because a dataset may appear homogeneous at a coarse level, yet reveal substantial heterogeneity upon closer inspection. For example, a collection of images may appear diverse at a high level, based on overall content, but exhibit less diversity when analyzed by specific features like color or texture at a finer scale. This multi-scale approach is vital in applications where detailed characterization of diversity is needed. This is because a comprehensive understanding of the data’s diversity across multiple scales is essential for tasks such as generative modeling, anomaly detection, and similarity analysis. It allows for a more robust and accurate assessment of diversity, capturing the full spectrum of variation in data distribution, something that single-scale analysis cannot achieve. This approach enables the development of more sophisticated and robust methods for evaluating the diversity of latent spaces, leading to a better understanding of data representations and more effective applications.
Magnitude Stability#
Magnitude stability, in the context of a research paper evaluating the diversity of latent representations using metric space magnitude, is a crucial concept. It addresses the robustness of the magnitude-based diversity measure to small perturbations in the data. A stable magnitude ensures that minor data variations do not drastically alter the computed diversity, which is critical for reliable model evaluation. The analysis likely explores the theoretical properties that guarantee this stability, potentially using concepts from topology or geometry. Empirical evidence demonstrating the stability under different noise levels and data transformations would also be presented. This could involve adding noise to the data, applying various transformations, or subsampling. The results would show that while there might be minor fluctuations, the overall magnitude and, consequently, the diversity measure remain consistent, providing confidence in the reliability of the approach. The level of stability achieved might be quantified by analyzing the sensitivity of the magnitude to noise or perturbations. This would involve measuring the change in magnitude as a function of some metric measuring the level of noise or perturbation. Such an analysis would contribute significantly to establishing the practical utility and reliability of using metric space magnitude for assessing diversity in the context of latent space analysis. The demonstration of magnitude stability would underscore its value as a powerful tool for understanding and comparing latent representations.
Diverse Embeddings#
The concept of “Diverse Embeddings” in a research paper likely refers to the creation and evaluation of vector representations (embeddings) that capture the diversity within a dataset. High-quality diverse embeddings are crucial for many machine learning tasks, as they ensure that the model is exposed to a broad range of features and patterns. A lack of diversity can lead to issues like mode collapse, where the model generates limited outputs, or under-representation, where some parts of the data are not adequately captured. The paper likely explores methods to promote diversity in embeddings, perhaps through techniques like data augmentation, loss function modifications, or architectural designs. The assessment of diversity is also key, and the paper probably presents novel ways of measuring this property, potentially moving beyond simple metrics towards more sophisticated evaluations that consider multi-scale relationships and capture the geometry of the embedding space. Evaluation may involve comparing different embedding generation methods or analyzing how diversity affects downstream task performance. The paper likely presents empirical results demonstrating the effectiveness of the proposed techniques and comparisons to existing approaches.
Future Directions#
Future research could explore extending metric space magnitude to handle diverse data modalities more effectively, perhaps by investigating alternative distance metrics or embedding techniques tailored to specific data types. Improving computational efficiency for large datasets remains crucial; exploring approximation methods or leveraging specialized hardware could unlock wider applicability. A deeper theoretical investigation into the relationship between magnitude and other diversity measures would enhance understanding and facilitate comparisons. Combining magnitude with other diversity metrics offers promising avenues, allowing for a more holistic assessment of latent space quality. Finally, applying magnitude to assess diversity in novel domains, such as reinforcement learning or time-series analysis, could reveal unexpected insights and further demonstrate its versatility as a robust and interpretable tool for evaluating diversity in diverse domains. Formalizing axiomatic properties and proving further theoretical guarantees related to magnitude’s behavior under various conditions would strengthen its foundation and enhance its adoption in the broader machine learning community.
More visual insights#
More on figures
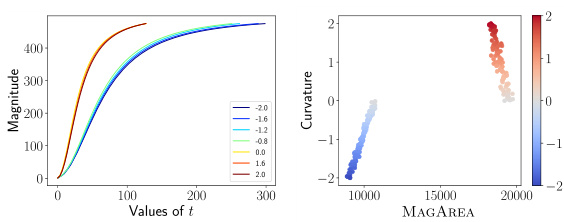
🔼 This figure shows that magnitude functions can capture curvature information. The left panel displays magnitude functions for unit disks with different curvatures, ranging from -2 to 2. The right panel demonstrates a linear relationship between the area under the magnitude function (MAGAREA) and the curvature value. This indicates that MAGAREA serves as a good predictor of curvature and can effectively capture this geometric property.
read the caption
Figure 2: Magnitude detects curvature. Left: Magnitude functions for unit disks with varying curvature between [-2,2]. Right: MAGAREA exhibits a linear relationship with curvature, indicating that it serves as a expressive predictor.

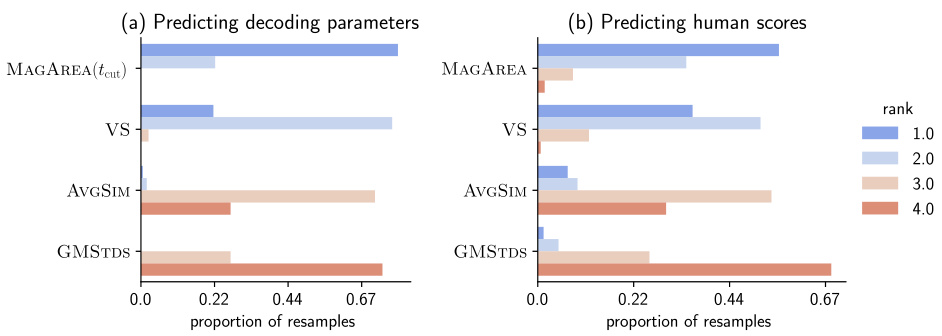
🔼 The figure compares MAGAREA with three other diversity measures (VS, AVGSIM, GMSTDS) in predicting the ground truth diversity of generated sentences across three tasks (prompt, resp, story) and five embedding models. The softmax temperature controls the diversity of generated sentences. MAGAREA consistently outperforms the other methods.
read the caption
Figure 3: MAGAREA outperforms alternative diversity measures at predicting the ground truth-diversity of generated sentences, controlled by the softmax-temperature across 3 tasks and 5 embed-ding models. Baseline measures, AVGSIM and GMSTDS, perform worse in terms of the R2 scores.Points show the mean of the R² scores, while lines represent the standard deviations across 5-foldcross-validation (repeated 10 times).

🔼 This figure illustrates the diversity evaluation pipeline using metric space magnitude. It shows how the magnitude function captures the effective number of points at different scales, and how MAGAREA and MAGDIFF are used for reference-free and reference-based diversity evaluation, respectively.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

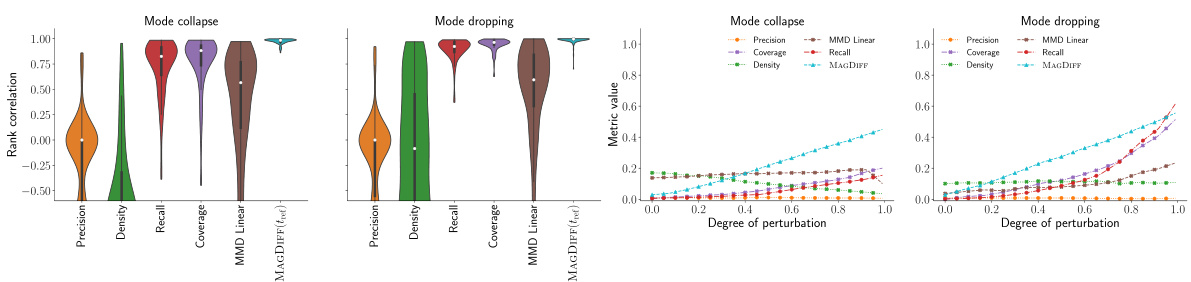
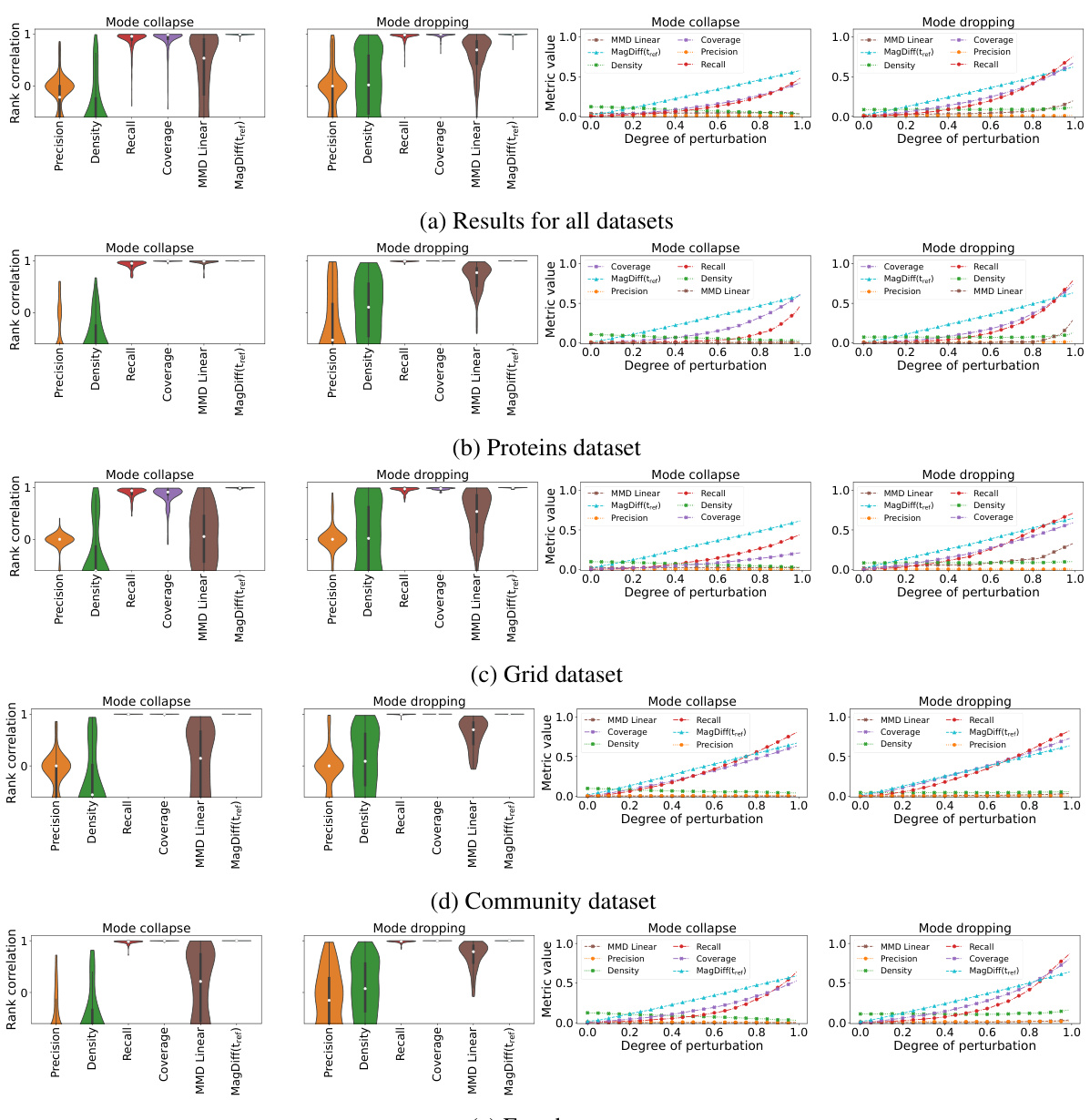
🔼 This figure compares different diversity metrics’ performance in detecting mode dropping in image embeddings. It demonstrates that MAGDIFF and MAG(0.5tref) accurately reflect the decrease in diversity regardless of whether modes are dropped simultaneously or sequentially. In contrast, recall and coverage metrics show inconsistencies, particularly in the sequential mode dropping scenario, overestimating the rate of diversity decrease.
read the caption
Figure 5: Magnitude correctly detects that diversity decreases in the same manner across simultaneous and sequential mode dropping outperforming recall and coverage. Lines show the mean values of each metric across 20 resamples, shaded areas the standard deviations.
🔼 This figure illustrates the pipeline for evaluating the diversity of latent representations using the proposed magnitude-based measures. It shows how the magnitude function captures the effective number of points at different scales, and how MAGAREA and MAGDIFF are used for reference-free and reference-based diversity evaluations, respectively.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.
🔼 This figure provides a visual overview of the diversity evaluation pipeline using metric space magnitude. It starts with an example of four latent spaces with varying diversity, then illustrates how the magnitude function captures the effective number of points at different scales. The figure shows how the area under the magnitude function (MAGAREA) can be used for reference-free diversity evaluation, while the difference in area between two magnitude functions (MAGDIFF) is utilized for reference-based diversity assessment. The figure highlights the multi-scale nature of the proposed method and its application in different scenarios.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X₂, X₃, and X₄, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

🔼 This figure shows the pipeline for evaluating the diversity of latent representations using the proposed magnitude-based measures. It illustrates how magnitude functions capture diversity at multiple scales and how MAGAREA and MAGDIFF are used for reference-free and reference-based diversity evaluations, respectively. Examples of latent spaces with varying diversity are provided to visualize the process.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

🔼 This figure provides a visual overview of the diversity evaluation pipeline proposed in the paper. It illustrates how the magnitude function is used to quantify diversity across multiple scales, culminating in two proposed measures: MAGAREA for reference-free diversity and MAGDIFF for reference-based diversity. The figure uses examples of latent spaces with varying diversity levels to showcase the methodology and interpretation of the results.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X1 is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

🔼 This figure provides a visual overview of the diversity evaluation pipeline proposed in the paper. It illustrates how magnitude functions are used to quantify the intrinsic diversity of latent representations, both with and without a reference distribution. Panel (a) shows example latent spaces with varying diversity. Panel (b) explains the concept of a magnitude function, which represents the effective number of points at different scales. Panels (c), (d), and (e) illustrate how MAGAREA and MAGDIFF, two novel diversity measures based on the area under the magnitude function, are used for reference-free and reference-based diversity evaluations respectively.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.
🔼 This figure provides a visual overview of the diversity evaluation pipeline using the proposed magnitude-based measures. It illustrates how the magnitude function captures the effective number of points at different scales, and how this information is used to define reference-free (MAGAREA) and reference-based (MAGDIFF) diversity measures. The figure uses four example latent spaces with varying diversity levels to demonstrate the approach, showcasing the relationship between the magnitude function, the proposed diversity measures, and the overall diversity of the latent space.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X₂, X₃, and X₄, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

🔼 This figure provides a visual overview of the diversity evaluation pipeline using the proposed magnitude-based measures. It showcases how magnitude functions capture diversity at multiple scales and how MAGAREA and MAGDIFF are used for reference-free and reference-based diversity evaluations, respectively.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

🔼 This figure provides a visual overview of the diversity evaluation pipeline proposed in the paper. It uses a series of example latent spaces to illustrate how the magnitude function is calculated and used to define measures of intrinsic diversity (MAGAREA) and the difference in diversity between two spaces (MAGDIFF). The figure highlights the multi-scale nature of the approach and shows how it can be used for both reference-free and reference-based diversity evaluation.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X₂, X₃, and X₄, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

🔼 The figure shows the performance of MAGAREA and other diversity measures in predicting the ground truth diversity of generated sentences for three different tasks and five embedding models. The x-axis represents the R-squared values for different diversity measures, while the y-axis represents the embedding models and tasks. The results demonstrate that MAGAREA consistently outperforms the other measures, highlighting its effectiveness in quantifying diversity.
read the caption
Figure 3: MAGAREA outperforms alternative diversity measures at predicting the ground truth-diversity of generated sentences, controlled by the softmax-temperature across 3 tasks and 5 embed-ding models. Baseline measures, AVGSIM and GMSTDS, perform worse in terms of the R2 scores.Points show the mean of the R² scores, while lines represent the standard deviations across 5-foldcross-validation (repeated 10 times).

🔼 This figure compares the performance of MAGAREA against other diversity metrics in predicting ground truth diversity scores for generated sentences. The diversity of the sentences was controlled by varying the softmax temperature across three different tasks and five different embedding models. MAGAREA shows significantly better performance (higher R-squared values) than the baseline methods (AVGSIM and GMSTDS), indicating that it’s a more effective measure for quantifying intrinsic diversity in this context.
read the caption
Figure 3: MAGAREA outperforms alternative diversity measures at predicting the ground truth-diversity of generated sentences, controlled by the softmax-temperature across 3 tasks and 5 embed-ding models. Baseline measures, AVGSIM and GMSTDS, perform worse in terms of the R2 scores. Points show the mean of the R² scores, while lines represent the standard deviations across 5-fold cross-validation (repeated 10 times).

🔼 This figure compares the performance of MAGAREA against other diversity metrics (VS, AVGSIM, GMSTDS) in predicting the ground truth diversity of generated sentences. The diversity is controlled by adjusting the softmax temperature across three different sentence generation tasks (prompt, resp, story) and five different embedding models. The results show that MAGAREA significantly outperforms the baselines, as measured by R-squared values.
read the caption
Figure 3: MAGAREA outperforms alternative diversity measures at predicting the ground truth-diversity of generated sentences, controlled by the softmax-temperature across 3 tasks and 5 embed-ding models. Baseline measures, AVGSIM and GMSTDS, perform worse in terms of the R2 scores.Points show the mean of the R² scores, while lines represent the standard deviations across 5-foldcross-validation (repeated 10 times).
🔼 This figure provides a visual overview of the diversity evaluation pipeline proposed in the paper. It illustrates how magnitude functions, which represent the effective number of points in a space at different scales, are used to measure both intrinsic and comparative diversity. The figure shows examples of latent spaces with varying diversity, their corresponding magnitude functions, and the calculations of MAGAREA and MAGDIFF as measures of diversity.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

🔼 This figure provides a visual overview of the proposed diversity evaluation pipeline using metric space magnitude. It demonstrates how magnitude functions capture multi-scale diversity, and introduces MAGAREA and MAGDIFF as novel measures for intrinsic and reference-based diversity evaluation respectively.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.
🔼 This figure illustrates the diversity evaluation pipeline proposed in the paper. It shows how the magnitude function, a multi-scale measure of diversity, is used to evaluate both the intrinsic diversity of latent representations (reference-free) and the difference in diversity between two representations (reference-based). The figure includes examples of different latent spaces with varying diversity levels, their corresponding magnitude functions, and how MAGAREA and MAGDIFF are used to quantify and compare their diversity.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.

🔼 This figure demonstrates the effectiveness of the proposed MAGDIFF metric in measuring the change in diversity under mode collapse and mode dropping scenarios. It compares the performance of MAGDIFF to other metrics like recall and coverage. The results show that MAGDIFF accurately captures the decrease in diversity regardless of whether modes are dropped sequentially or simultaneously, while the other methods exhibit inaccurate or inconsistent behavior.
read the caption
Figure 5: Magnitude correctly detects that diversity decreases in the same manner across simultaneous and sequential mode dropping outperforming recall and coverage. Lines show the mean values of each metric across 20 resamples, shaded areas the standard deviations.

🔼 This figure compares different diversity metrics in the context of mode dropping (the inability of a model to capture all parts of an input distribution) in image generative models. It shows how the magnitude-based measure (MAGDIFF) accurately reflects the decrease in diversity whether modes are dropped simultaneously or sequentially. In contrast, recall and coverage metrics are shown to be less accurate and sensitive to the order of mode dropping.
read the caption
Figure 5: Magnitude correctly detects that diversity decreases in the same manner across simultaneous and sequential mode dropping outperforming recall and coverage. Lines show the mean values of each metric across 20 resamples, shaded areas the standard deviations.
🔼 This figure illustrates the diversity evaluation pipeline proposed in the paper. It starts with an example showing four latent spaces with varying diversity levels. The pipeline then uses the magnitude function to assess diversity across multiple scales (local and global), identifying a convergence scale (tconv) to define the evaluation interval. The area under the magnitude function (MAGAREA) quantifies intrinsic diversity in reference-free scenarios, while the difference in areas (MAGDIFF) is used for reference-based comparison. The example shows how the approach distinguishes different spaces based on their diversity.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.
🔼 This figure provides a visual overview of the diversity evaluation pipeline proposed in the paper. It showcases how magnitude functions are used to quantify diversity at multiple scales and how these functions can be summarized to obtain reference-free and reference-based diversity metrics. The figure includes examples to illustrate how diversity varies across different latent spaces and how the proposed metrics can capture these variations.
read the caption
Figure 1: Overview of our diversity evaluation pipeline. (a) We start with an example of four latent spaces with 200 points, varying in diversity. (b) The magnitude function measures the effective number of points at t, a scale of distance between observations. When the scale factor t almost equals zero, magnitude is close to 1, and a space effectively looks like one point. For large t, the number of effective points is noticeably higher and magnitude converges towards the cardinality. We find the approximate convergence scale, tconv, at which magnitude almost equals the cardinality, and use it to define the evaluation interval T across which diversity changes most notably. (c) The more diverse the space, the higher the value of its magnitude function. By construction, X₁ is more diverse than X2, X3, and X4, respectively, as we can see from the effective size of each space. We leverage this behaviour to define novel multi-scale indicators of diversity. (d) Our proposed measure of intrinsic diversity, MAGAREA, summarises the area under each magnitude function for reference-free diversity evaluation. (e) In a reference-based setting, we assess the difference in diversity using MAGDIFF, the area between two magnitude functions.
More on tables

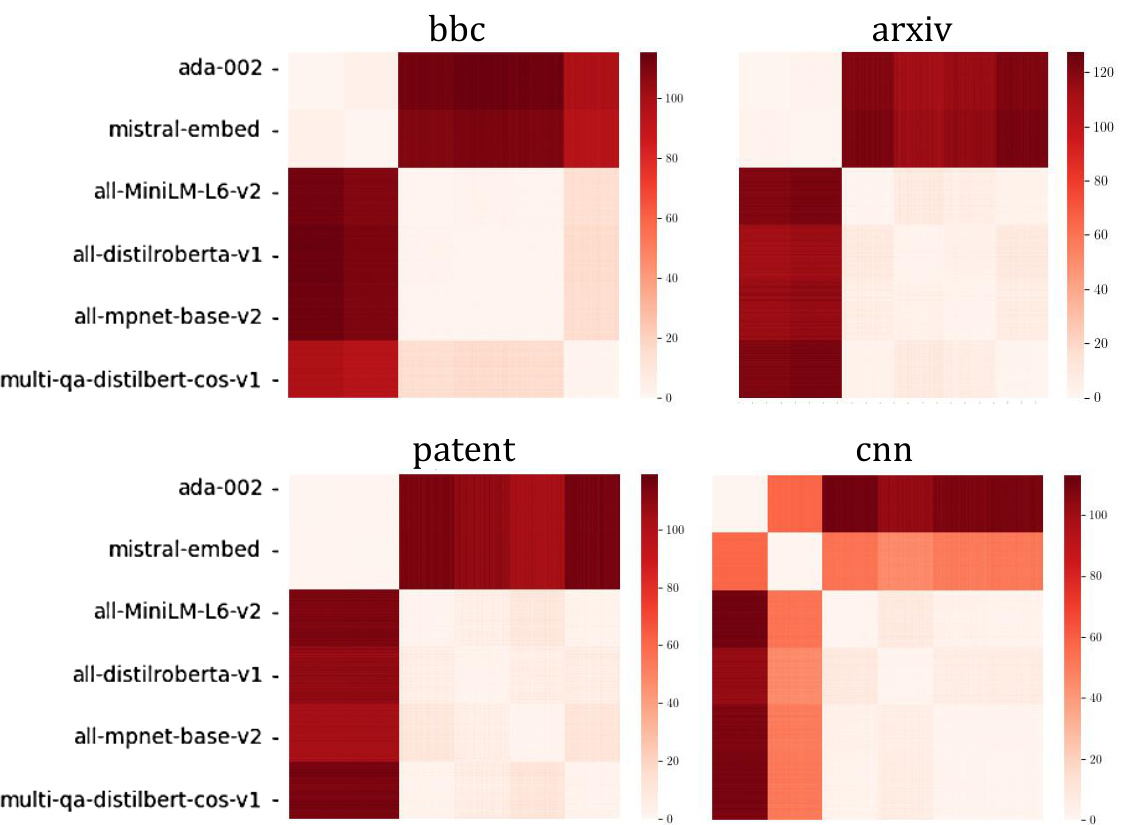
🔼 This table presents the results of a 5-NN classification experiment to determine whether embedding models can be distinguished based solely on their intrinsic diversity. The experiment uses six different embedding models and four different datasets (cnn, patents, arXiv, bbc). The table shows the classification accuracy for each embedding model using four different diversity measures: MAGDIFF, AVGSIM, VS, and GMSTDS. The experiment is conducted twice, once with no pre-processing of the embeddings and once with PCA pre-processing. The results show that MAGDIFF consistently achieves the highest accuracy in distinguishing between the embedding models, demonstrating the effectiveness of magnitude as a measure of intrinsic diversity.
read the caption
Table 2: Magnitude characterises text embedding models. We show the accuracy (↑) of different diversity scores for distinguishing between six embedding models, using a 5-NN classifier.
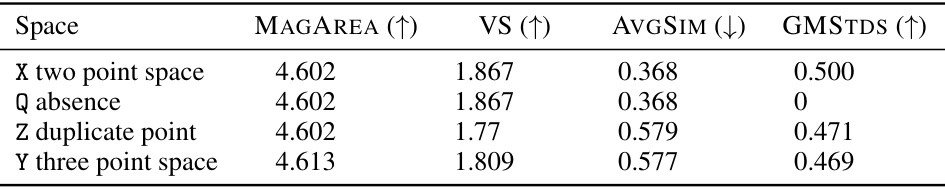
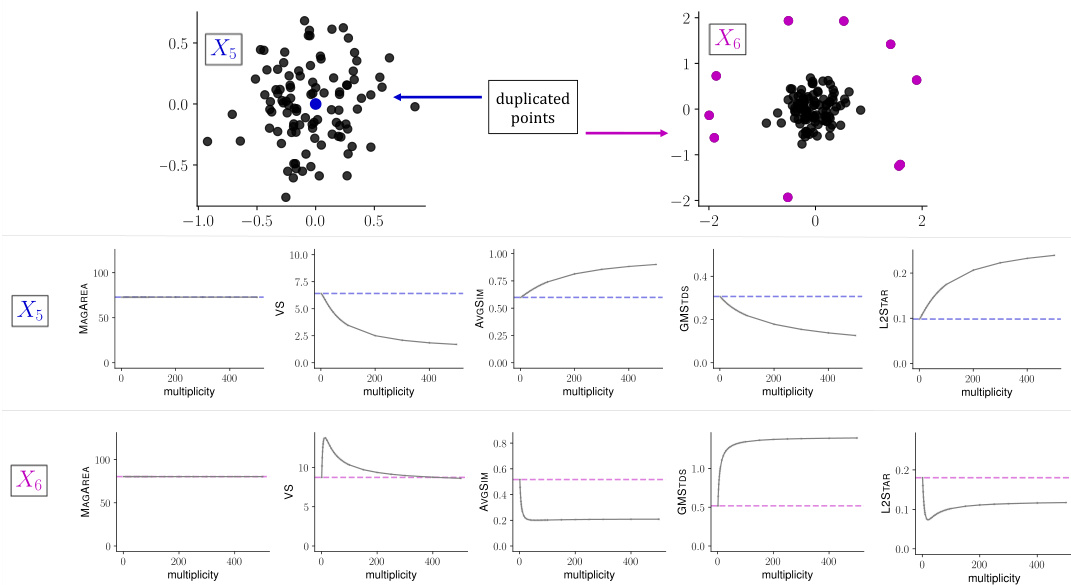
🔼 This table demonstrates the failure of several common diversity measures (VS, AVGSIM, GMSTDS) to satisfy fundamental axioms of diversity, which are: twin property (adding a duplicate observation does not change diversity), absence invariance (removing unobserved features does not change diversity), and monotonicity in observations (adding new observations does not decrease diversity). The table presents four scenarios (spaces X, Q, Z, Y) showing how the baseline measures fail these checks, highlighting their limitations. In contrast, MAGAREA successfully fulfills these properties in all cases, demonstrating its theoretical soundness.
read the caption
Table S.1: Counterexamples demonstrating that alternative diversity measures fail to fulfil fundamental axioms of diversity, whereas magnitude passes these sanity checks.

🔼 This table compares four different diversity measures (MAGAREA, VS, AVGSIM, GMSTDS, and L2STAR) across four simulated datasets (X1-X4) representing varying levels of diversity. The datasets are visually represented in Figure 1a) of the main paper and represent different distributions of points, ranging from uniformly distributed (high diversity) to highly clustered (low diversity). The table demonstrates that MAGAREA accurately reflects the intuitive understanding of diversity, correctly ranking the datasets from most to least diverse, unlike the other metrics which fail to capture the differences between the datasets.
read the caption
Table S.2: MAGAREA shows the correct order in diversity when comparing the simulated examples in Figure 1a) from the main text. In contrast, two baseline diversity measures, AVGSIM and GMSTDS, as well as the discrepancy measure L2STAR fail to distinguish that the random point pattern, X1, is more diverse than the clustered point pattern, X2.

🔼 This table presents the mean R-squared values achieved by various diversity metrics in predicting the decoding parameter (softmax temperature), along with standard deviations and 95% percentile intervals. The metrics are MAGAREA, VS, AVGSIM, and GMSTDS, tested across three tasks (Prompt, Resp, Story). It shows the relative performance of each metric in predicting the decoding parameter, which serves as a proxy for ground truth diversity.
read the caption
Table S.3: The mean performance of each diversity measure in terms of R² scores for predicting the decoding parameter. We also report 95% percentile intervals of these scores as well as standard deviations.
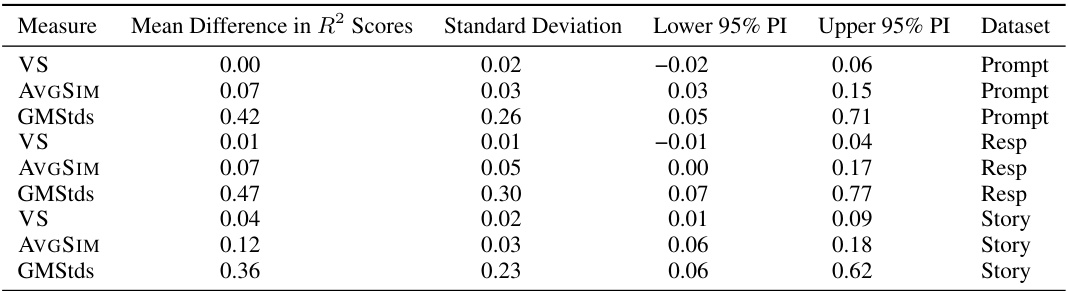
🔼 This table compares the performance of MAGAREA against other diversity measures (VS, AVGSIM, GMStds) in predicting decoding parameters. It shows the mean difference in R² scores between each alternative measure and MAGAREA, along with standard deviations and 95% percentile intervals. This allows for a more detailed analysis of the relative performance of MAGAREA compared to the baseline methods for each task (prompt, resp, story).
read the caption
Table S.4: The difference between each diversity measure and MAGAREA in terms of the difference in R² scores when predicting the decoding parameter. We also report 95% percentile intervals of these differences and standard deviations.

🔼 This table presents the results of a 5-NN classification task to distinguish between six different embedding models of the bbc dataset. The classification is performed using different diversity scores (MAGDIFF, AVGSIM, VS, GMSTDS) and varying numbers of nearest neighbors (k). The table shows the accuracy of the classification for each diversity score and value of k, demonstrating the consistent performance of MAGDIFF across different values of k. The results are analogous to those in Table 2 of the main text, which compares performance across different datasets.
read the caption
Table S.5: Classification performance remains consistent across varying choices of k for k-NN classification. We show the accuracy (↑) of different diversity scores for distinguishing between six embedding models of the bbc dataset, using PCA pre-processing and a k-NN classifier across varying values of k. These results are analogous to Table 2 in the main text.
Full paper#