↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world applications, such as recommendation systems, suffer from the problem of missing data, where the missing values are often “missing not at random” (MNAR). This poses significant challenges to predictive model accuracy as standard methods struggle to provide unbiased estimates with bounded variances. Existing techniques, like regularization, often fail to adequately address this issue, leading to unstable and unreliable model performance. The issue is further compounded as attempts to achieve unbiased estimation often result in unbounded variances.
This research introduces a novel framework that directly addresses this critical problem. The key innovation is a fine-grained dynamic learning approach, which adaptively selects the best estimator for each data point based on a defined objective function. This approach not only reduces bias and variance but also provides theoretical guarantees on the boundedness of variance and generalization error. The paper demonstrates the effectiveness of this dynamic framework through extensive experiments, showcasing significant improvements in predictive performance and robustness compared to existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers dealing with missing-not-at-random (MNAR) data, a prevalent issue in various fields like recommendation systems and online advertising. It offers a novel fine-grained dynamic learning framework that effectively addresses the limitations of existing methods in handling MNAR data, opening new avenues for research on bias-variance optimization and improving predictive model performance.
Visual Insights#

This figure visualizes the key factors and the objective function used in the dynamic estimator design. Panel (a) shows the surface of hst (bias determining factor), (b) shows the surface of hest (variance determining factor), and (c) illustrates the combined objective function w1(hest)² + w2hest which balances bias and variance. Finally, (d) presents the optimal objective values, showing how the optimal value of the objective function varies with the propensity (pu). This demonstrates how the framework dynamically adapts to various propensities, optimizing both bias and variance.

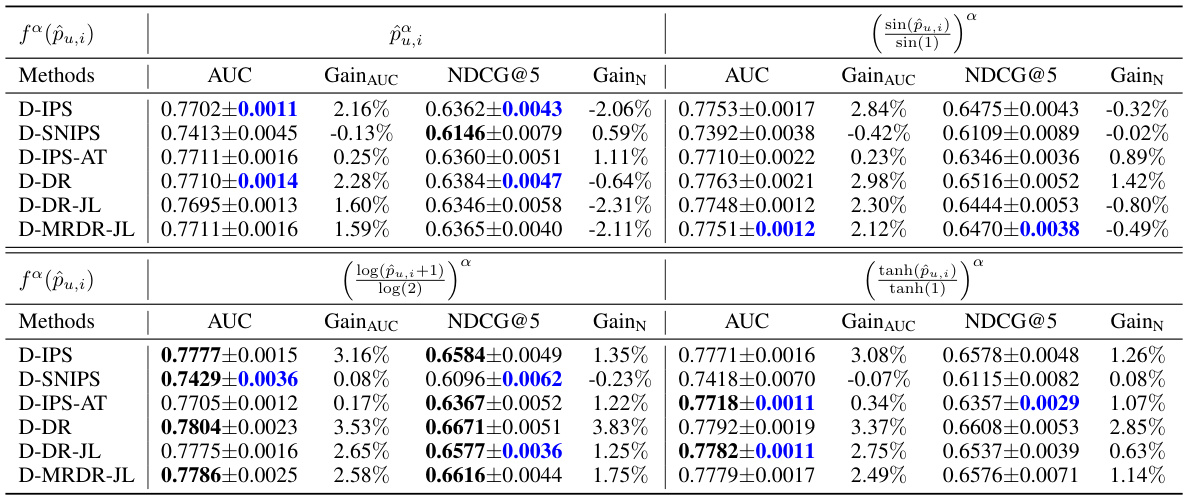
This table presents four different functions, f(pu,i), used in the dynamic estimator framework. Each function is designed to balance bias and variance in the context of missing-not-at-random data. The table also shows the specific expressions for bias (hB) and variance (hV) terms resulting from each of the four functions. These hB and hV expressions are key components in the bias-variance joint optimization strategy proposed in the paper, allowing the framework to adaptively select estimators that achieve a balance between bias and variance for each user-item pair.
In-depth insights#
MNAR Bias Issue#
The core issue lies in handling missing data not at random (MNAR). Standard approaches often assume data is Missing At Random (MAR) or even Missing Completely At Random (MCAR), leading to biased and unreliable model estimations. MNAR data introduces sample selection bias, where the probability of missingness depends on the unobserved values. This bias significantly impacts the accuracy and generalization of models trained on such data. Traditional methods like imputation or weighting techniques struggle to address this issue effectively, especially when propensity scores (the probability of observing a value) are near zero. The paper highlights that simply eliminating bias often results in unbounded variance, so there is a need for a quantitative joint optimization of bias and variance. This requires moving beyond simple bias-variance trade-offs and adopting adaptive strategies that carefully balance the two, using appropriate estimators suited to the data characteristics.
Dynamic Estimators#
The concept of “Dynamic Estimators” in the context of handling data missing not at random (MNAR) is a significant advancement. Instead of using a single, static estimation method, dynamic estimators adapt their approach based on the characteristics of each data point (e.g., user-item pair). This adaptability is crucial for MNAR data, where the probability of missingness varies across data points. By considering the specific properties of each instance, dynamic estimators can reduce bias and variance while simultaneously bounding generalization errors. This joint optimization of bias and variance is a key theoretical contribution and represents a paradigm shift from traditional static methods, which typically focus on only one of these factors. The proposed framework showcases a fine-grained approach that allows for selecting an estimator tailored to each situation, leading to improved performance and robustness. The dynamic nature enhances the adaptability and ultimately the predictive accuracy of the models in real-world scenarios where MNAR data is pervasive.
Bias-Variance Tradeoff#
The bias-variance tradeoff is a central concept in machine learning, representing the tension between model accuracy and generalizability. High bias indicates that a model is overly simplistic and fails to capture underlying data patterns, leading to underfitting. Conversely, high variance suggests a model is excessively complex, fitting noise in the training data and thus generalizing poorly to unseen data, resulting in overfitting. The optimal model achieves a balance between these extremes, minimizing both bias and variance to achieve optimal predictive performance. This balance is context-dependent, varying with data characteristics and problem complexity. Techniques like regularization, cross-validation, and ensemble methods are employed to manage this tradeoff, aiming to find a model with sufficient complexity to capture essential patterns while avoiding excessive complexity that would lead to overfitting and poor generalization.
Regularization Limits#
The concept of ‘Regularization Limits’ in machine learning, particularly within the context of addressing bias and variance in models trained on data with missing not at random (MNAR) values, is a crucial one. Standard regularization techniques often fall short in this scenario because they primarily target variance reduction without fully considering the intricate interplay between bias and variance, especially when dealing with MNAR data. The inherent limitations stem from the fact that unbiasedness, while desirable, can conflict with achieving bounded variance. Attempts to reduce variance via regularization might introduce or amplify bias, rendering the model unstable or less effective in generalization. The core issue is that simple bias-variance trade-offs are insufficient; a more nuanced, quantitative joint optimization of bias and variance is necessary, particularly when propensity scores approach zero. Fine-grained, dynamic approaches that adapt to the specific characteristics of each data point are required to circumvent these limits and obtain models that are both robust and accurate.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the dynamic framework to encompass a broader range of missing data mechanisms beyond MNAR is crucial. Investigating the impact of different propensity score estimation methods on the framework’s performance would also be valuable. Developing more sophisticated objective functions for bias-variance trade-off optimization could further enhance the model’s predictive accuracy and robustness. Additionally, exploring the applicability of the framework to various downstream tasks beyond recommendation systems is warranted, potentially including tasks in natural language processing or computer vision. Finally, a comprehensive study comparing the fine-grained dynamic approach to existing state-of-the-art methods on diverse benchmark datasets is needed for robust evaluation and to highlight the unique advantages of this novel approach.
More visual insights#
More on tables
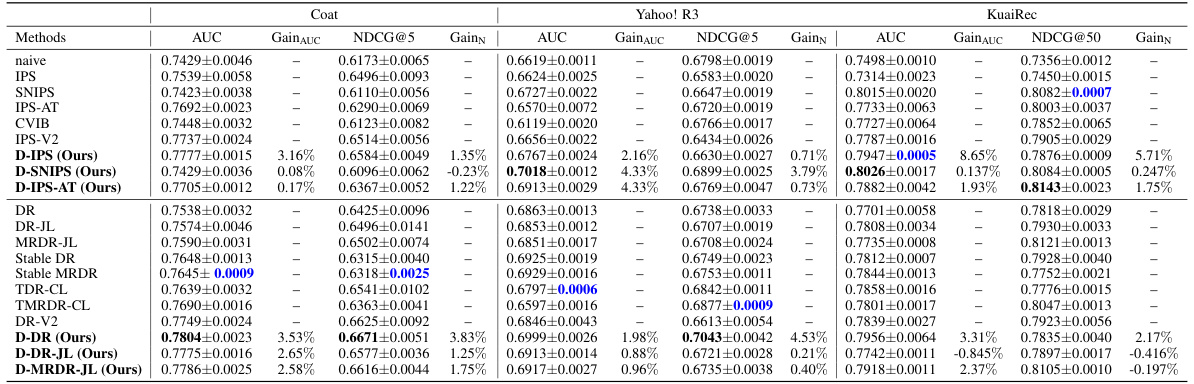
This table presents the performance comparison of the proposed dynamic learning framework against various state-of-the-art (SOTA) methods. The performance metrics used are AUC (Area Under the ROC Curve) and NDCG@5 (Normalized Discounted Cumulative Gain at 5). The results are shown for three datasets: Coat, Yahoo! R3, and KuaiRec. For each dataset and method, the mean and standard deviation of the metrics across 10 runs are displayed. GainAUC and GainNDCG represent the percentage improvement in AUC and NDCG@5 respectively, compared to the corresponding baseline.
This table presents the performance comparison of the proposed dynamic learning framework with existing state-of-the-art (SOTA) approaches on three real-world datasets (COAT, Yahoo! R3, and Kuairec). The performance metrics used are AUC and NDCG@5 (for COAT and Yahoo! R3) and NDCG@50 (for Kuairec). For each dataset and metric, the mean and standard deviation of the results across ten runs are shown for each method. The ‘GainAUC’ and ‘GainNDCG’ columns show the relative improvement of the dynamic methods over the respective baseline methods.

This table presents the bias and variance formulas for four different estimators: naive, EIB, IPS, and DR. Each formula shows how the bias and variance are calculated based on the prediction error (eu,i), the imputed error (êu,i), the propensity score (pu,i), and the indicator variable (δu,i). The formulas highlight the dependence of bias and variance on the propensity scores, particularly showing that unbiasedness may lead to unbounded variance when propensity scores approach zero.
Full paper#



















