TL;DR#
Logical Credal Networks (LCNs) offer a powerful framework for handling uncertainty and imprecision in probabilistic reasoning. However, performing abductive reasoning tasks, like finding the most probable explanation for observed evidence (MAP inference), is computationally challenging, especially for large networks. This limits the applicability of LCNs in complex real-world scenarios.
This research addresses this challenge by developing novel algorithms for solving MAP and Marginal MAP inference queries in LCNs. The paper proposes both exact search-based algorithms and approximate methods to handle larger problem instances. Extensive experiments demonstrate the effectiveness of the proposed techniques on various LCN instances, including randomly generated networks and realistic use cases. The approximate methods especially prove successful in tackling larger problems, expanding the applicability of LCNs to more complex situations. The key contribution is the improvement in scalability and efficiency of abductive reasoning within the LCN framework, making it more suitable for real-world applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with imprecise knowledge representation and reasoning. It introduces novel algorithms for abductive reasoning tasks, particularly in the context of Logical Credal Networks (LCNs), offering efficient solutions for problems previously intractable due to computational complexity. This work opens up new avenues for research in areas where uncertainty and imprecision are significant, such as diagnosis, abduction, and explanation in complex real-world applications.
Visual Insights#
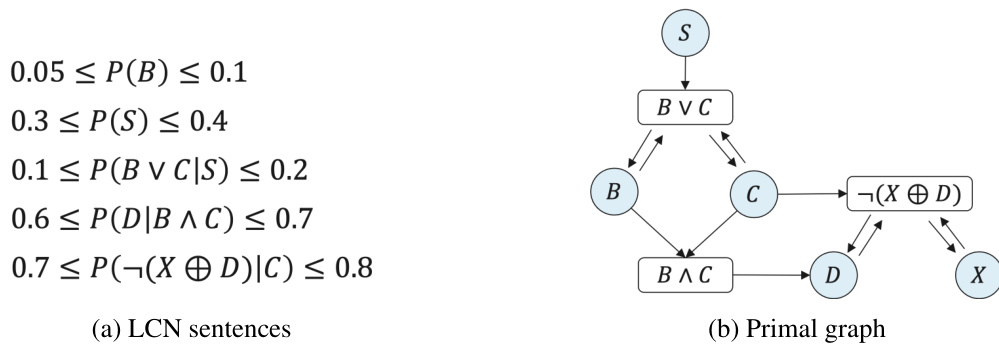
🔼 This figure shows a simple example of a Logical Credal Network (LCN) and its corresponding primal graph. The LCN sentences define probability bounds for different logical combinations of propositions (B, S, C, D, X). The primal graph visually represents the dependencies between these propositions, reflecting the structure of the LCN.
read the caption
Figure 1: A simple LCN and its primal graph.
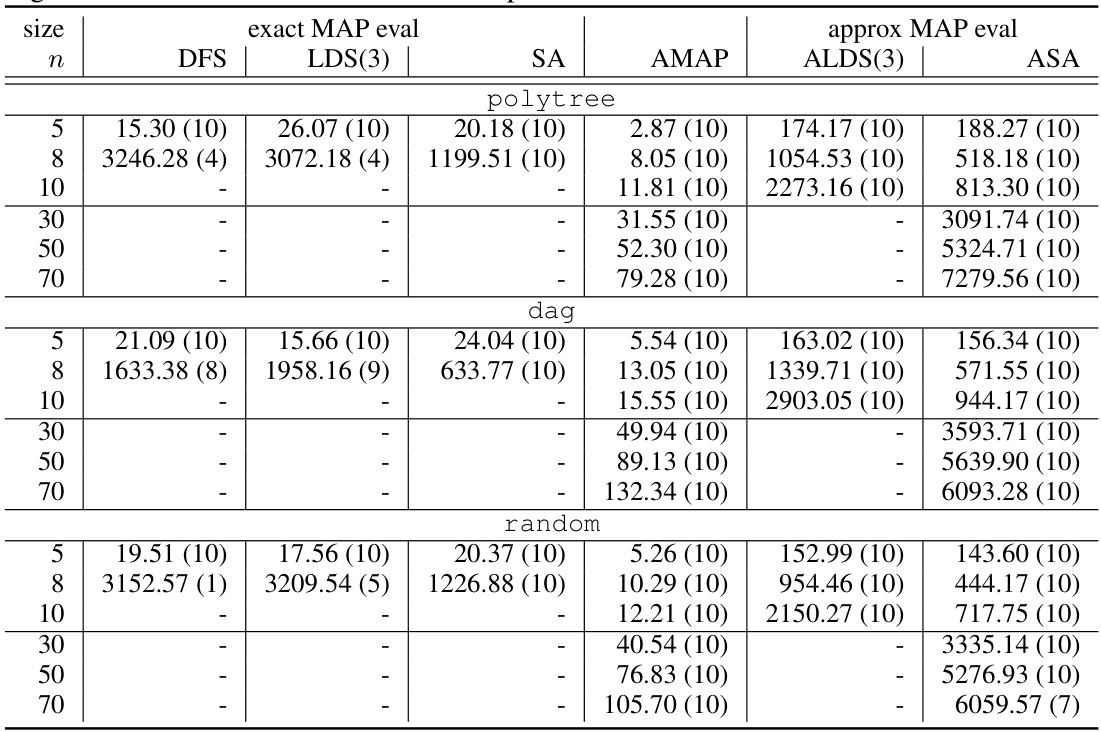
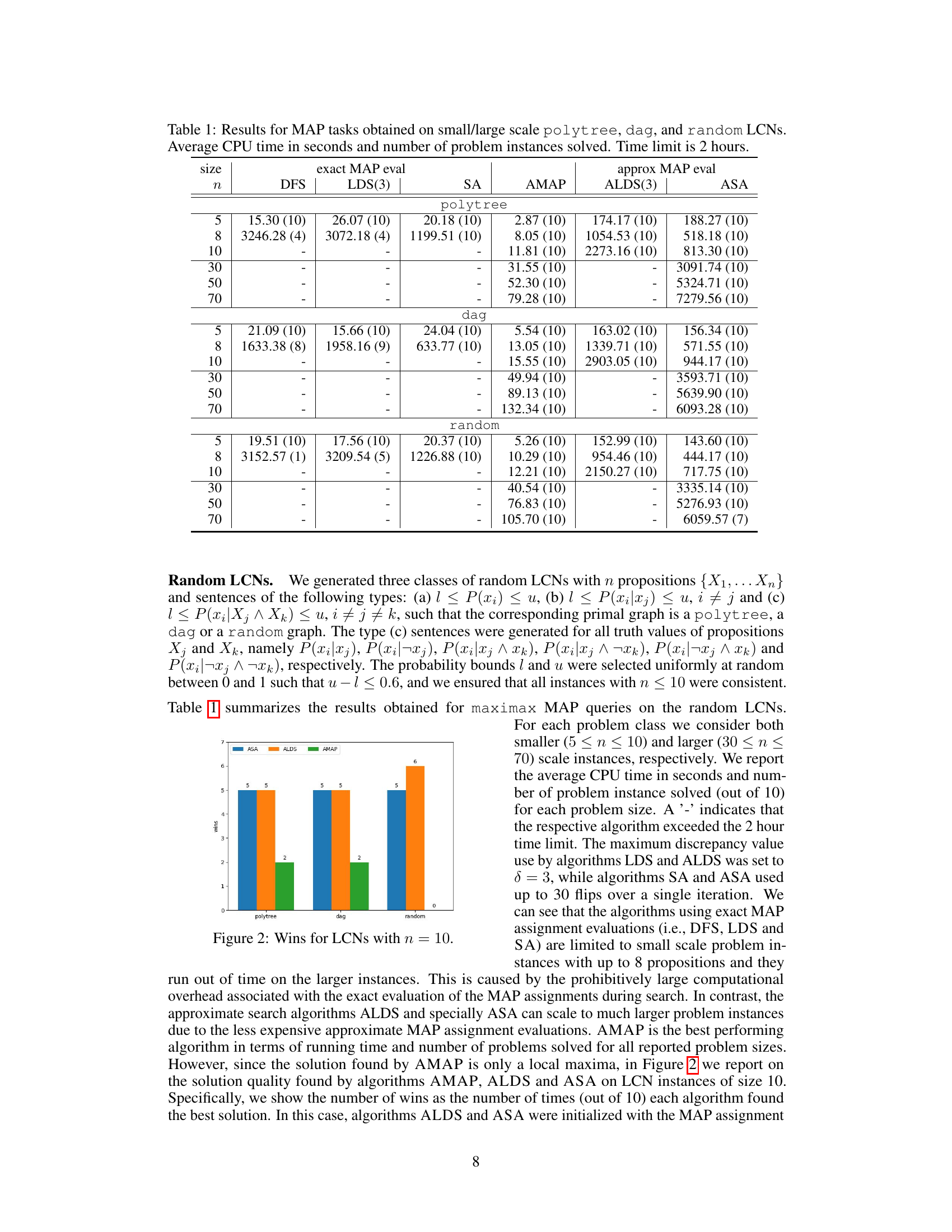
🔼 This table presents the results of the Maximum A Posteriori (MAP) inference experiments performed on three different types of Logical Credal Networks (LCNs): polytree, directed acyclic graph (DAG), and random LCNs. The experiments were conducted on both small (5-10 nodes) and larger (30-70 nodes) networks. The table shows the average CPU time (in seconds) and the number of problem instances solved within a 2-hour time limit for each algorithm and network type. The algorithms compared include Depth-First Search (DFS), Limited Discrepancy Search (LDS) with a discrepancy of 3, Simulated Annealing (SA), Approximate MAP (AMAP), Approximate LDS (ALDS) with a discrepancy of 3, and Approximate SA (ASA).
read the caption
Table 1: Results for MAP tasks obtained on small/large scale polytree, dag, and random LCNs. Average CPU time in seconds and number of problem instances solved. Time limit is 2 hours.
In-depth insights#
LCN Abductive Inference#
LCN abductive inference tackles the challenge of explaining evidence within Logical Credal Networks (LCNs). Unlike traditional probabilistic graphical models, LCNs handle imprecise probabilities and can represent cyclic relationships, making inference more complex. The core problem involves identifying the most probable (or plausible) explanations for observed evidence, often framed as finding maximum a posteriori (MAP) or marginal MAP (MMAP) assignments. Exact methods for solving these problems are computationally expensive and thus typically limited to smaller LCNs. The paper explores efficient approximate algorithms such as message passing and heuristic search methods (like simulated annealing and limited discrepancy search) to scale to larger problems. Approximate methods trade-off computational cost for solution quality, often providing near-optimal solutions, although it’s crucial to evaluate the trade-off in various applications. The work highlights a crucial need for efficient inference algorithms in the face of realistic, complex uncertain scenarios where cycles and imprecise probabilities are common features.
Exact MAP Search#
Exact MAP (Maximum a Posteriori) search algorithms, in the context of probabilistic reasoning models like Logical Credal Networks (LCNs), aim to find the most probable complete assignment of values to variables given observed evidence. The core challenge lies in the computational complexity, especially for LCNs which handle uncertainty by representing sets of probability distributions. Exact methods generally utilize exhaustive search or depth-first search strategies to explore all possible assignments. While guaranteeing optimality, these exact algorithms suffer from scalability issues, becoming computationally intractable even for moderately sized problems. The high computational cost stems from the need to evaluate the exact probability of each assignment, which often involves solving complex optimization problems. Thus, despite their theoretical appeal, the practical utility of exact MAP search in LCNs is severely limited by their exponential time complexity. Researchers frequently resort to approximation algorithms, which sacrifice optimality for scalability, to tackle larger problems.
Approximate Schemes#
The section on “Approximate Schemes” would likely detail methods to address the computational cost of exact MAP and Marginal MAP inference in Logical Credal Networks (LCNs). Exact methods, while providing precise solutions, become intractable for large-scale problems. Approximate schemes offer a trade-off: sacrificing some precision for improved efficiency. This could involve techniques such as message-passing algorithms, which iteratively refine probability estimates by propagating information across the network’s structure, or heuristic search strategies, like Simulated Annealing or Limited Discrepancy Search, that explore the solution space intelligently. The discussion would likely compare the accuracy and efficiency of different approximation techniques, highlighting scenarios where approximations are particularly beneficial. A key consideration would be the impact of approximation on the reliability of the resulting abductive reasoning. The paper would need to justify that any loss of precision is acceptable given the gains in computational scalability. This section is crucial for demonstrating the practical applicability of LCNs to real-world problems, where datasets often involve numerous propositions.
Empirical Evaluation#
A robust empirical evaluation section is crucial for validating the claims made in a research paper. It should demonstrate the effectiveness of proposed methods by comparing them against existing approaches using appropriate metrics. The selection of datasets is vital, ensuring they represent diverse scenarios and potential challenges. Clear methodology regarding experimental setup, parameter tuning, and statistical significance testing must be detailed. Results should be presented concisely yet comprehensively, possibly with visual aids like graphs and tables, highlighting both strengths and weaknesses. The discussion of results should go beyond mere observation, providing insightful analysis and relating findings to the broader research context. Reproducibility is paramount, and sufficient detail on dataset sources, code, and computational resources are essential for future validation and comparison. Finally, limitations of the evaluation should be acknowledged transparently, such as dataset bias, or limitations in scope, thereby maintaining the integrity and value of the research.
Future Directions#
Future research could explore more sophisticated search algorithms for MAP and MMAP inference in LCNs, such as improved branch and bound or best-first search methods, potentially incorporating advanced heuristics. Developing novel bounding techniques to guide the search process more effectively would be crucial. Furthermore, research should investigate more efficient approximation schemes for marginal inference within LCNs, which is a significant computational bottleneck. This might involve exploring alternative message-passing algorithms or leveraging advanced optimization techniques. Extending the framework to handle larger-scale problems more effectively is a primary goal, and this will require both algorithmic innovations and possibly exploring distributed or parallel computing approaches. Finally, applying LCNs to new problem domains and evaluating their performance against existing methodologies would be essential to demonstrate their practical utility and identify areas for future enhancement.
More visual insights#
More on figures
🔼 This figure shows a simple example of a Logical Credal Network (LCN) and its corresponding primal graph. The LCN is represented by a set of sentences specifying probability bounds on logical formulas involving propositions such as Bronchitis (B), Smoking (S), Cancer (C), Dyspnea (D), and X-Ray result (X). The primal graph visually depicts the relationships between these propositions and formulas, illustrating the network’s structure.
read the caption
Figure 1: A simple LCN and its primal graph.
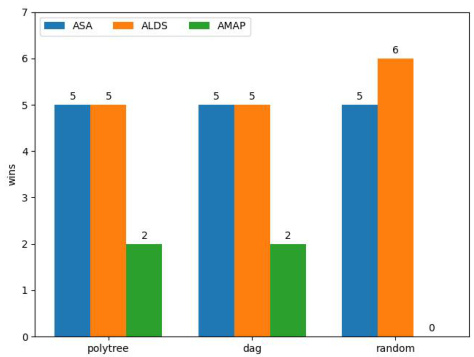
🔼 This figure shows the number of times (out of 10) that each algorithm (ASA, ALDS, and AMAP) found the best solution for LCNs with 10 propositions. For each of the three types of LCNs (polytree, DAG, and random), the bar chart displays the number of wins for each algorithm. It highlights the relative performance of the approximate search algorithms (ALDS and ASA) compared to the approximate message-passing algorithm (AMAP) in finding high-quality solutions.
read the caption
Figure 2: Wins for LCNs with n = 10.
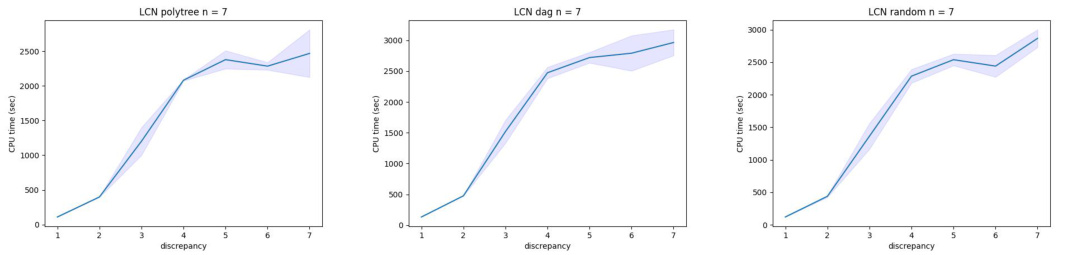
🔼 This figure shows the average CPU time and standard deviation of the Approximate Limited Discrepancy Search (ALDS) algorithm for different discrepancy values (δ). The results are presented for three different types of Logical Credal Networks (LCNs): polytree, DAG, and random, each with 7 propositions (n=7). The shaded area represents the standard deviation, illustrating the variability in runtime for each discrepancy level.
read the caption
Figure 3: Average CPU time in seconds and standard deviation vs discrepancy δ for ALDS(δ).
More on tables
🔼 This table presents the results of applying different algorithms (exact and approximate) to solve Marginal MAP (MMAP) inference tasks on a set of realistic Logical Credal Networks (LCNs). The algorithms’ performance is evaluated based on CPU time in seconds, with a time limit of 2 hours. The table shows that exact methods struggle with larger networks while approximate methods can scale better.
read the caption
Table 2: Results for MMAP tasks on realistic LCNs. CPU time in seconds. Time limit is 2 hours.
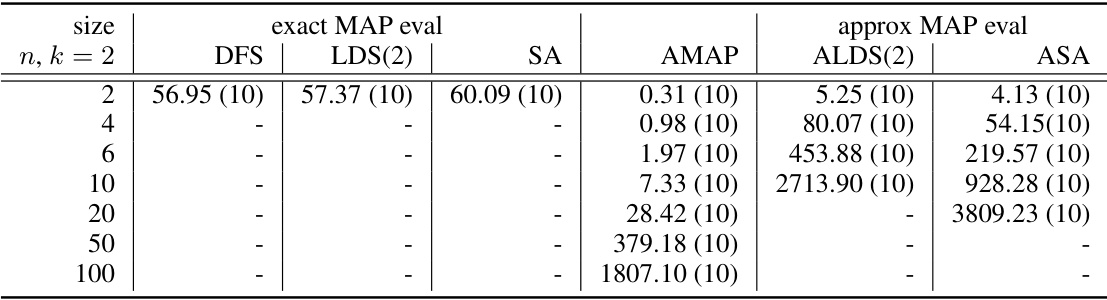
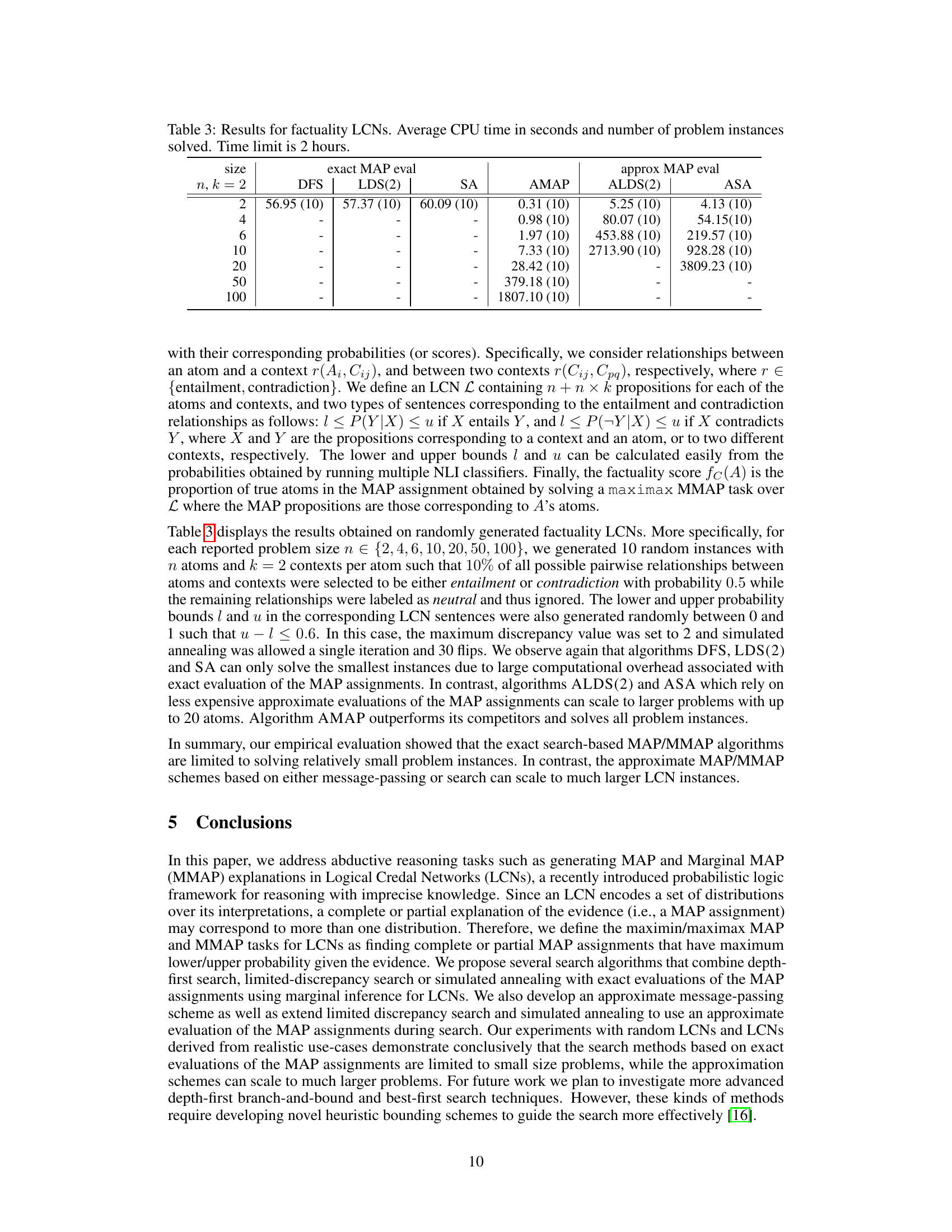
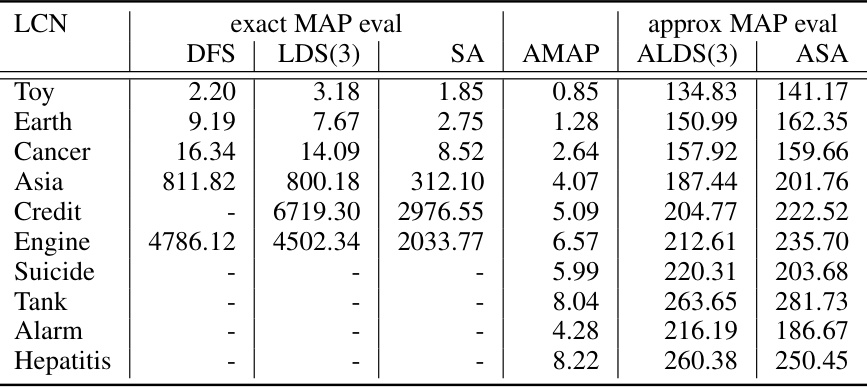
🔼 This table presents the results of experiments on factuality LCNs, focusing on the performance of different MAP inference algorithms (exact and approximate). It shows the average CPU time and the number of problem instances solved within a 2-hour time limit for various problem sizes (n, k = 2). The algorithms are categorized into exact MAP evaluation methods (DFS, LDS(2), SA) and approximate MAP evaluation methods (AMAP, ALDS(2), ASA). The table highlights the scalability challenges of exact methods as problem size increases, contrasting with the improved performance of approximation-based methods in larger instances.
read the caption
Table 3: Results for factuality LCNs. Average CPU time in seconds and number of problem instances solved. Time limit is 2 hours.
Full paper#