TL;DR#
Graph Neural Networks (GNNs) heavily rely on the ‘homophily’ assumption—that connected nodes share similar characteristics. However, existing homophily metrics often fail to accurately predict GNN performance. This paper identifies this problem and explores why conventional methods are insufficient.
The authors propose a novel approach to address this limitation. They introduce ‘Tri-Hom’, a composite metric that disentangles graph homophily into three crucial aspects: label, structural, and feature homophily. Extensive experiments on synthetic and real-world datasets demonstrate Tri-Hom’s superior predictive power compared to 17 existing metrics, highlighting the importance of considering these three homophily aspects synergistically for a complete understanding of GNN behavior.
Key Takeaways#
Why does it matter?#
This paper is crucial for GNN researchers. It challenges the limitations of existing homophily metrics by introducing a novel composite metric, Tri-Hom, which considers label, structural, and feature aspects. This significantly improves correlation with GNN performance, opening new avenues for understanding and improving GNNs in both theory and practice.
Visual Insights#
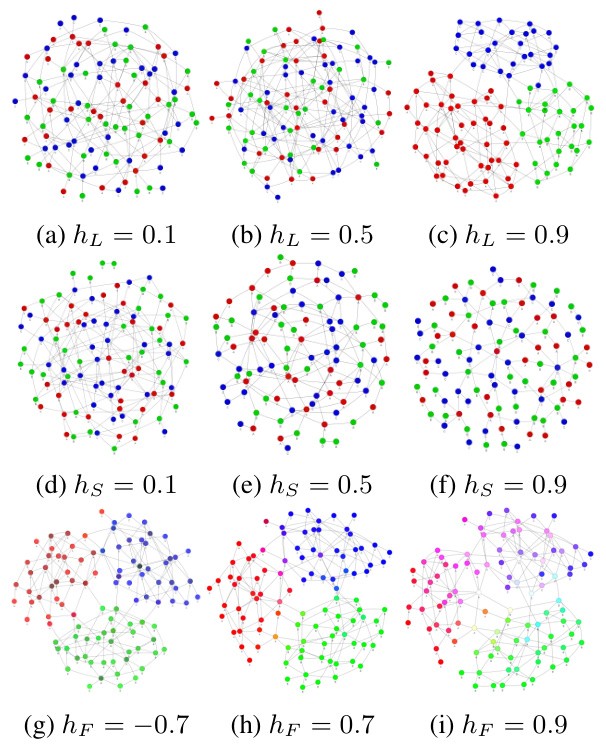
🔼 This figure visualizes synthetic graphs generated using the Contextual Stochastic Block Model with three types of Homophily (CSBM-3H). It demonstrates how varying levels of label homophily (a-c), structural homophily (d-f), and feature homophily (g-i) affect the graph structure and node features. Different colors represent different node classes or feature values, illustrating how these homophily aspects influence node clustering and feature distributions within the graph.
read the caption
Figure 1: Visualization of synthetic graphs generated by CSBM-3H with varying levels of label homophily, structural homophily, and feature homophily. The node colors denote node classes in sub-figure (a-f) and node features in sub-figure (g-i)
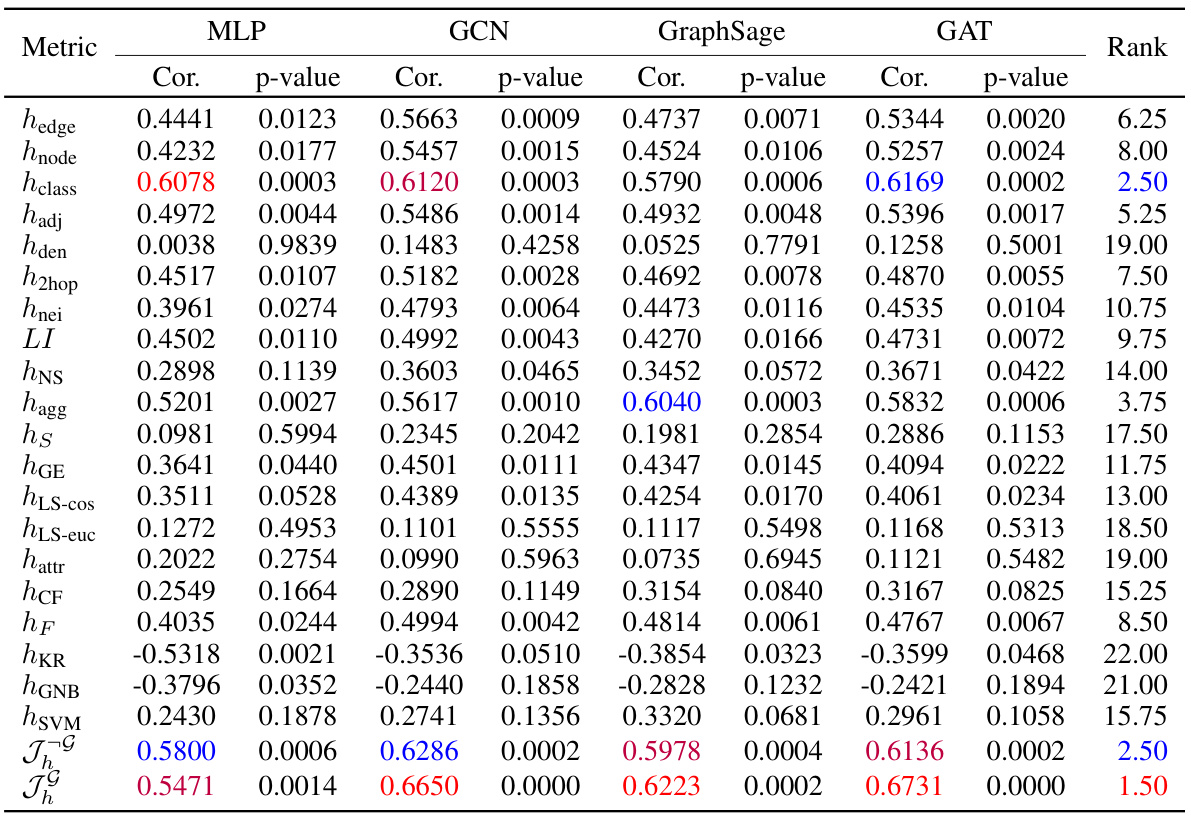
🔼 This table shows the Pearson correlation and p-value between 17 existing homophily metrics and the proposed Tri-Hom metric, and the performance of four node classification models (MLP, GCN, GraphSage, GAT) on 31 real-world datasets. The table helps to evaluate the ability of each metric to predict the performance of graph neural networks (GNNs) on node-level tasks. The rank column provides a summary of the overall predictive ability of each metric across the different models. A lower rank indicates better predictive ability.
read the caption
Table 1: Pearson correlation with p-value of all the metrics with model performance of node classification on 31 real-world datasets.
In-depth insights#
Homophily’s Limits#
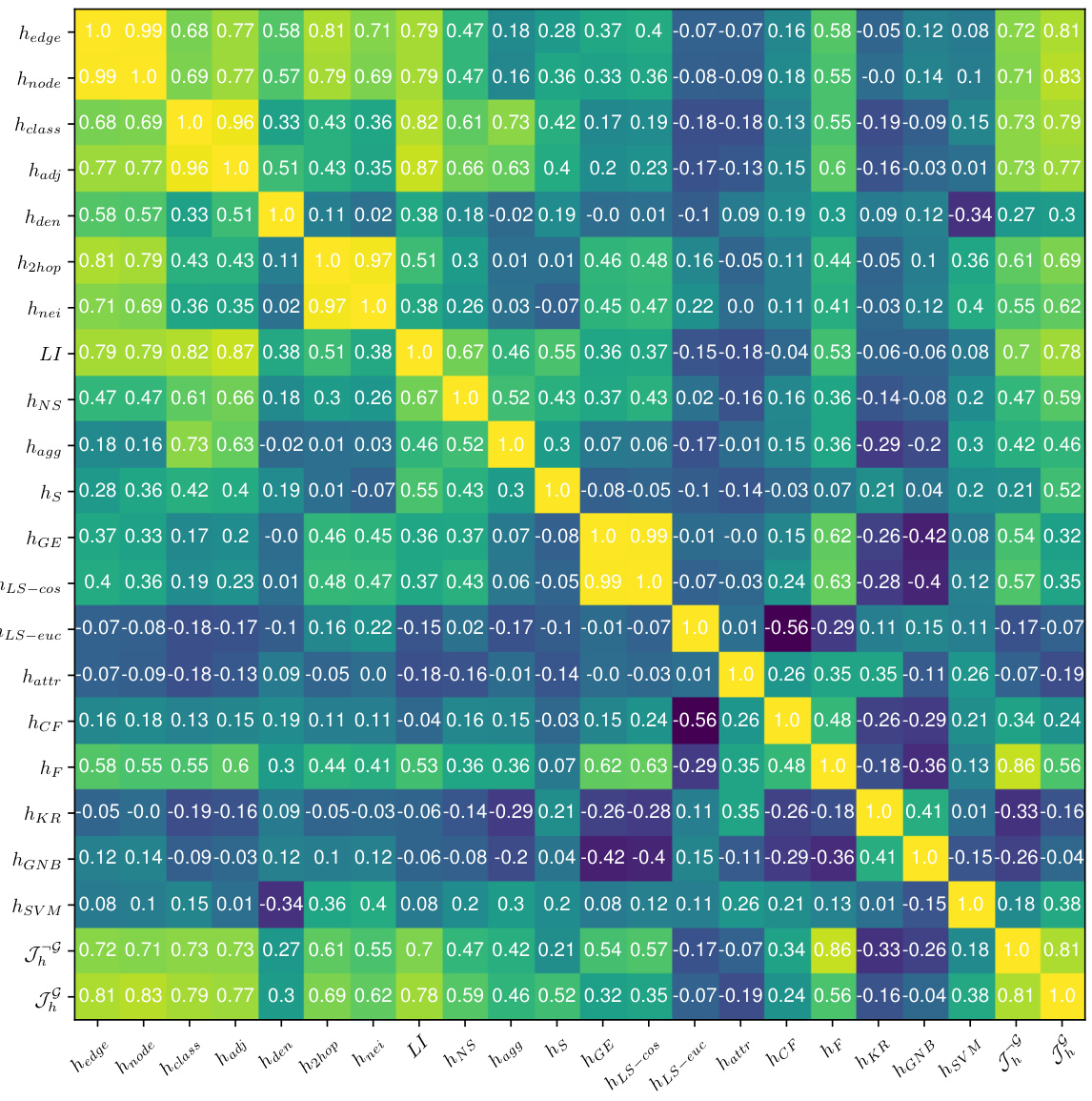
The concept of homophily, where similar nodes connect in a graph, is central to Graph Neural Networks (GNNs). However, the relationship between homophily and GNN performance is complex and not fully understood. Existing homophily metrics often fail to capture the nuances of real-world graph structures, leading to inconsistencies between measured homophily and observed GNN accuracy. This limitation arises because conventional metrics typically focus solely on label homophily (similarity in node labels), neglecting crucial aspects like structural homophily (consistency of neighborhood structures) and feature homophily (dependencies between node features). A more comprehensive understanding requires disentangling homophily into these three facets. This disentanglement reveals that the synergy between label, structural, and feature homophily is key to predicting GNN performance, highlighting the limitations of single-aspect homophily metrics. Future research should focus on developing more robust metrics that incorporate these multifaceted aspects of homophily, leading to improved GNN design and a deeper understanding of their capabilities and limitations in various applications.
Tri-Homophily Metric#
The proposed “Tri-Homophily Metric” offers a novel approach to understanding graph homophily by decomposing it into three distinct aspects: label, structural, and feature homophily. This multifaceted perspective addresses limitations of traditional metrics which often focus solely on label consistency. By incorporating structural and feature dependencies, Tri-Homophily provides a more comprehensive evaluation of how node similarity influences graph neural network (GNN) performance. This holistic measure is expected to improve correlation with GNN performance, overcoming the limitations of single-aspect metrics which may not fully capture the complexity of real-world graphs. The synergistic effects of the three homophily types, as highlighted by the metric, offer valuable insights into GNN behavior and explain previously observed phenomena such as the mid-homophily pitfall and the impact of feature shuffling. CSBM-3H, a generative model incorporating all three homophily aspects, supports Tri-Homophily’s theoretical validity and practical effectiveness, showing its potential as a crucial tool for GNN research and development.
CSBM-3H Model#
The CSBM-3H model is a significant contribution, introducing a novel approach to understanding graph homophily’s multifaceted influence on Graph Neural Networks (GNNs). Instead of relying solely on label homophily, CSBM-3H disentangles homophily into three crucial aspects: label, structural, and feature homophily, reflecting the synergistic interplay of node labels, graph topology, and node features. This nuanced perspective addresses the limitations of previous models that focus solely on label consistency. The model’s strength lies in its ability to generate synthetic graphs with controlled levels of these three homophily types. This allows for systematic investigation and a deeper understanding of how each aspect impacts GNN performance. The theoretical analysis, backed by synthetic and real-world experiments, reveals the superiority of a composite metric (Tri-Hom) which considers the synergy of all three homophily aspects. Tri-Hom demonstrates a significantly stronger correlation with GNN performance compared to existing metrics that consider only single homophily aspects, highlighting the importance of the holistic view provided by CSBM-3H. This framework is a crucial step towards more accurate and reliable assessment and design of GNNs.
Synthetic Datasets#
The use of synthetic datasets in evaluating graph neural network (GNN) performance, particularly concerning graph homophily, offers several advantages. Synthetic data allows for precise control over various graph properties, including the degree of homophily, network topology, and feature distributions, enabling researchers to isolate and study the effects of specific factors on GNN performance. This controlled environment is crucial because real-world datasets often exhibit complex interdependencies and confounding variables that make it difficult to draw definitive conclusions. By systematically varying homophily levels in synthetic data, researchers can build a more complete understanding of how homophily impacts GNNs and identify potential performance pitfalls. However, a critical limitation lies in the generalizability of findings from synthetic data to real-world scenarios. Real-world graphs are far more complex and heterogeneous than synthetic ones, potentially exhibiting distributions of node features, relationships, and network structures that are not captured in artificial datasets. Therefore, while synthetic data provides valuable insights for controlled experiments, its use should be complemented by rigorous testing on diverse real-world datasets to ensure that conclusions are broadly applicable and robust.
Future Directions#
The “Future Directions” section of this research paper suggests several promising avenues for future work. Disentangling graph homophily beyond the current label, structural, and feature aspects is crucial, especially exploring more generalized settings without restrictive assumptions like uniform node degrees or balanced classes. Investigating the interplay of homophily types in unsupervised or weak-supervised scenarios, especially important in label-scarcity settings, is highlighted. Improving model design is a key focus, with suggestions to use the developed understanding to refine GNNs by improving their ability to handle diverse structural patterns, heterophily levels, and feature dependencies. Specific applications like recommendation systems and social network analysis are emphasized, urging the exploration of how the disentangled homophily framework can deliver new insights and improved performance in these domains. The overall direction is towards a more nuanced and comprehensive approach to understanding graph homophily, impacting both theoretical advancements and the practical application of GNNs to real-world problems.
More visual insights#
More on figures
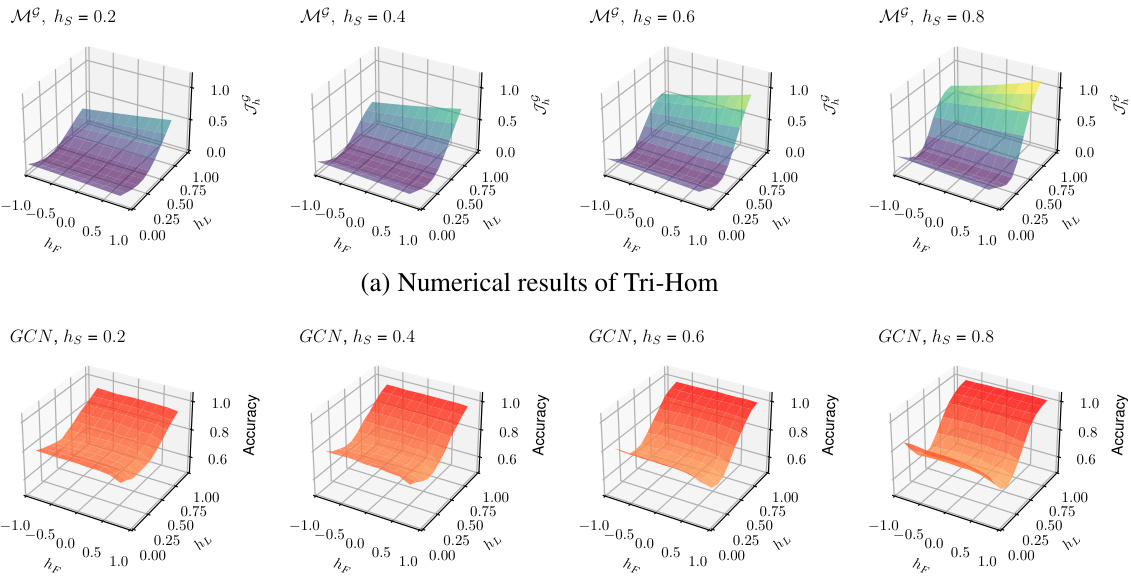
🔼 This figure shows the impact of label homophily (hL), feature homophily (hF), and structural homophily (hs) on both the numerical results of Tri-Hom and the model performance (GCN) using synthetic datasets generated by CSBM-3H. The left panel displays the numerical values of Tri-Hom calculated using the formula derived from the theoretical analysis of CSBM-3H. The right panel illustrates the GCN node classification accuracy obtained from experiments on the synthetic graphs. Both panels visualize how changes in hL, hF, and hs affect Tri-Hom and GCN performance, respectively, across different values of hs. This comparison helps demonstrate how well the Tri-Hom metric captures the impact of graph homophily on GCN performance.
read the caption
Figure 2: We measure the impact of label homophily h₁, feature homophily hF, and structural homophily hs through numerical results of Tri-Hom R and simulation results of the node classification accuracy with GCN on synthetic datasets.

🔼 This figure visualizes the results of an experiment evaluating the impact of three types of graph homophily (label, feature, and structural) on the performance of a Graph Convolutional Network (GCN) for node classification. It compares numerical results of a composite metric called Tri-Hom with the actual GCN performance across a range of homophily levels. The results demonstrate the complex interplay between these homophily types and model performance.
read the caption
Figure 2: We measure the impact of label homophily h₁, feature homophily hF, and structural homophily hs through numerical results of Tri-Hom and simulation results of the node classification accuracy with GCN on synthetic datasets.
🔼 This figure visualizes the impact of label, feature, and structural homophily on both the numerical results of the Tri-Hom metric and the model performance (using GCN) on synthetic datasets. It shows 3D plots where the x-axis represents label homophily (h₁), the y-axis represents feature homophily (hF), and the z-axis represents the Tri-Hom value or model accuracy. Separate plots are shown for different levels of structural homophily (hs). The plots demonstrate the complex interplay between these three types of homophily and their combined effect on model performance.
read the caption
Figure 2: We measure the impact of label homophily h₁, feature homophily hF, and structural homophily hs through numerical results of Tri-Hom I and simulation results of the node classification accuracy with GCN on synthetic datasets.

🔼 This figure shows a comparison between the numerical results of Tri-Hom and the model performance on synthetic datasets generated by CSBM-3H with varying label homophily (hL), feature homophily (hF), and structural homophily (hs). Subfigures (a) and (b) show the impact of hL, hF, and hs on Tri-Hom and GCN’s node classification accuracy, respectively. The results demonstrate the alignment between the numerical results of Tri-Hom and GCN’s performance, highlighting the effectiveness of Tri-Hom in capturing the influence of the three aspects of homophily on GCN’s performance.
read the caption
Figure 2: We measure the impact of label homophily h₁, feature homophily hF, and structural homophily hs through numerical results of Tri-Hom I and simulation results of the node classification accuracy with GCN on synthetic datasets.
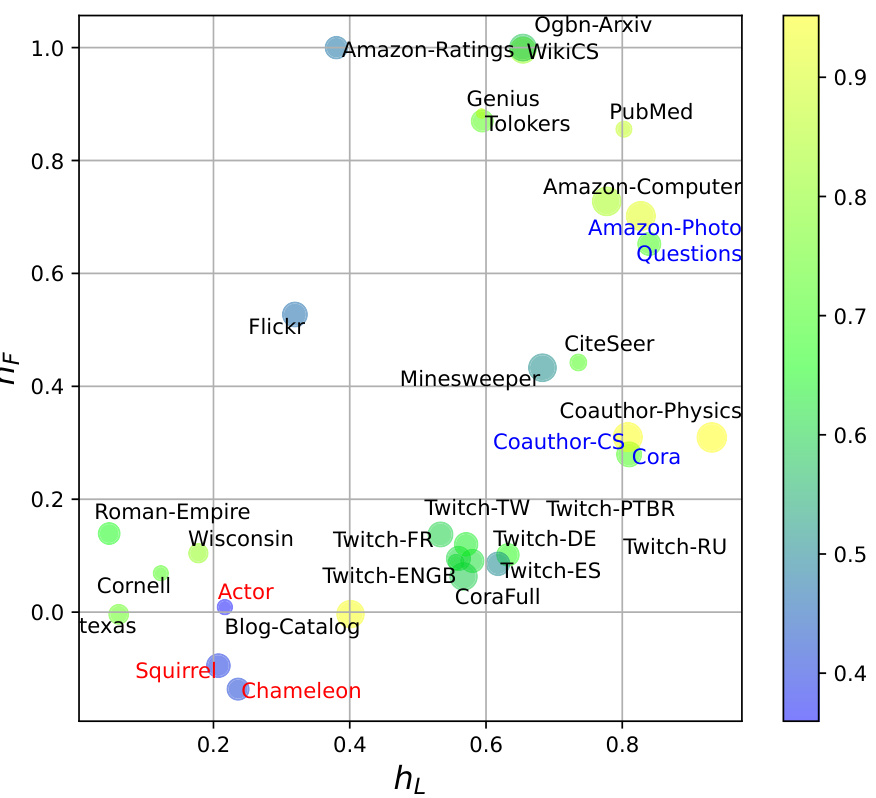
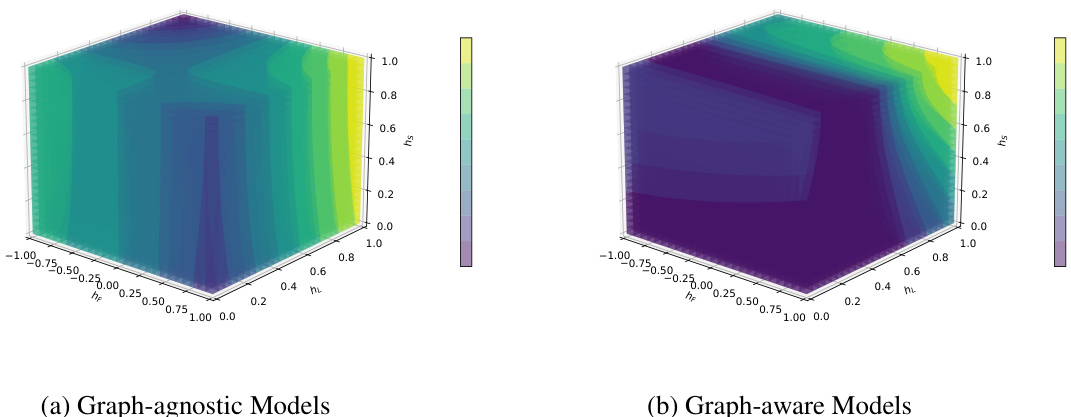
🔼 This figure visualizes the relationship between label homophily (hL), feature homophily (hF), structural homophily (hs), and the performance of Graph Convolutional Networks (GCNs) on 31 real-world datasets. Each data point represents a dataset; its x-coordinate corresponds to its label homophily, its y-coordinate to its feature homophily, and the size of the point represents its structural homophily. The color of the data point indicates the GCN classification accuracy on the dataset, ranging from low accuracy (blue) to high accuracy (yellow). The visualization helps understand how these three types of homophily interact and affect GCN performance.
read the caption
Figure 6: Label, feature, and structural homophily metrics on real-world datasets are shown as the x-axis, y-axis, and the size of the scatter respectively. The classification performance of GCN is denoted by the color of the scatters.

🔼 This figure shows a comparison of numerical results of the Tri-Hom metric and the performance of a Graph Convolutional Network (GCN) model on synthetic datasets. The impact of label homophily (h₁), feature homophily (hF), and structural homophily (hs) on both the Tri-Hom metric and GCN accuracy is visualized. The results demonstrate a strong correlation between the Tri-Hom metric and the GCN’s performance, highlighting the effectiveness of Tri-Hom in capturing the combined effect of these three homophily aspects.
read the caption
Figure 2: We measure the impact of label homophily h₁, feature homophily hF, and structural homophily hs through numerical results of Tri-Hom I and simulation results of the node classification accuracy with GCN on synthetic datasets.
🔼 This figure visualizes synthetic graphs generated using the Contextual Stochastic Block Model with three types of Homophily (CSBM-3H). It shows how varying levels of label homophily (a-c), structural homophily (d-f), and feature homophily (g-i) impact the generated graph structure. Different node colors represent different classes (a-f) or feature values (g-i).
read the caption
Figure 1: Visualization of synthetic graphs generated by CSBM-3H with varying levels of label homophily, structural homophily, and feature homophily. The node colors denote node classes in sub-figure (a-f) and node features in sub-figure (g-i)
More on tables
🔼 This table presents the Pearson correlation coefficients and their corresponding p-values between 18 different graph homophily metrics and the performance of four graph neural network models (MLP, GCN, GraphSage, and GAT) on 31 real-world datasets for node classification tasks. The metrics cover various aspects of homophily (label, structure, and features), and the purpose is to assess the correlation between homophily and GNN performance, helping to evaluate the predictive power of different homophily measures.
read the caption
Table 1: Pearson correlation with p-value of all the metrics with model performance of node classification on 31 real-world datasets.
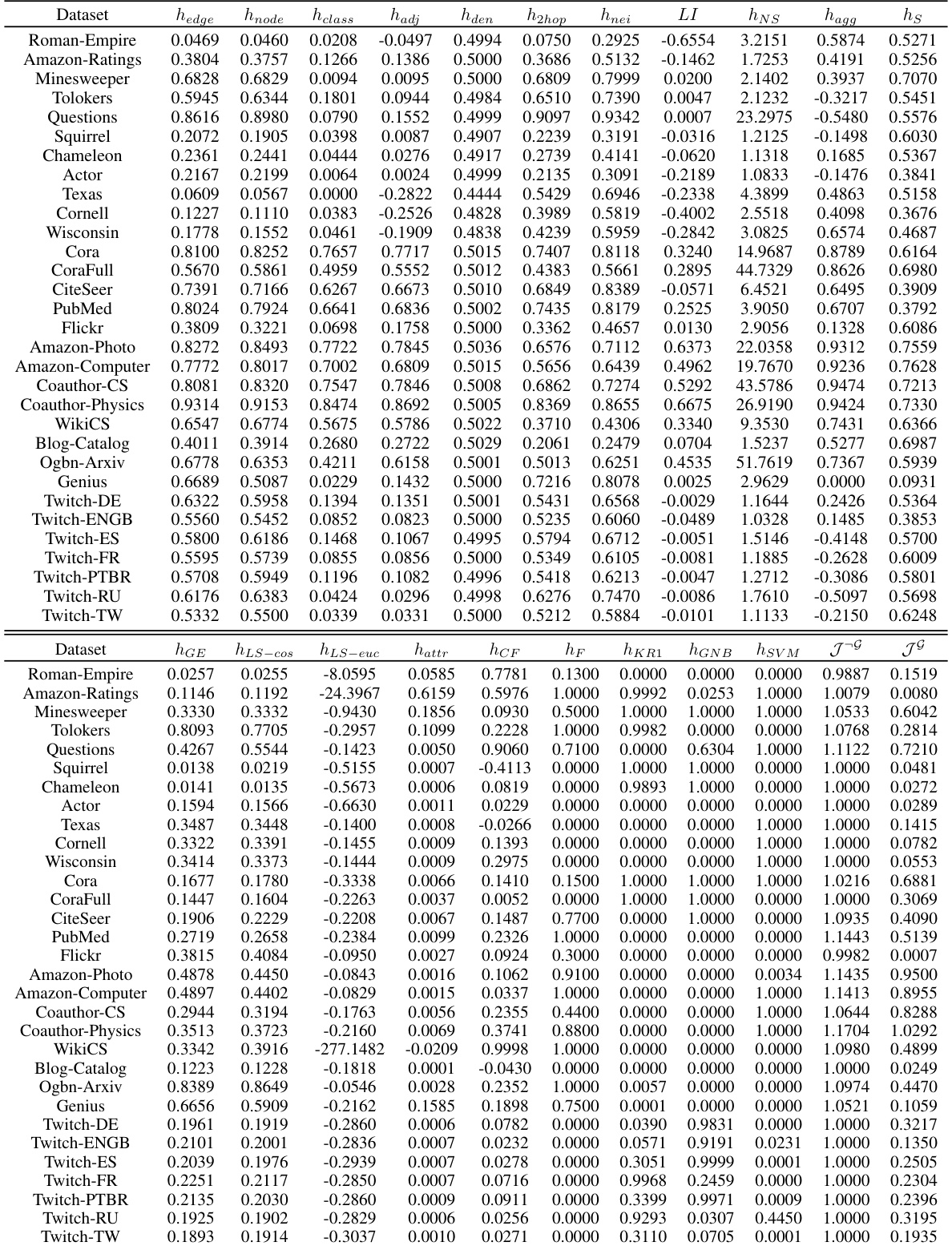
🔼 This table shows the Pearson correlation and p-values between 18 different homophily metrics and the performance of four different graph neural network models (MLP, GCN, GraphSage, and GAT) on 31 real-world datasets. The goal is to assess how well each metric correlates with the accuracy of node classification. A lower p-value indicates stronger statistical significance. The rank column provides the average rank of each metric across the four models.
read the caption
Table 1: Pearson correlation with p-value of all the metrics with model performance of node classification on 31 real-world datasets.

🔼 This table presents the Pearson correlation and p-values between 18 different graph homophily metrics and the performance of four node classification models (MLP, GCN, GraphSage, and GAT) on 31 real-world datasets. The metrics are categorized into label-based, structure-based, feature-based, and classifier-based homophily metrics. The table helps to evaluate the effectiveness of each metric in predicting model performance.
read the caption
Table 1: Pearson correlation with p-value of all the metrics with model performance of node classification on 31 real-world datasets.

🔼 This table presents the Pearson correlation coefficients and their corresponding p-values for various graph homophily metrics and node classification performance across 31 real-world datasets. It shows how well each metric correlates with the performance of four different graph neural network models (MLP, GCN, GraphSage, GAT). The lower the p-value, the more statistically significant the correlation. The rank column indicates the average rank of each metric across the four models based on the correlation strength, where lower ranks signify better predictive power of the metric.
read the caption
Table 1: Pearson correlation with p-value of all the metrics with model performance of node classification on 31 real-world datasets.

🔼 This table shows the Pearson correlation and p-value between 18 different graph homophily metrics and the performance (node classification accuracy) of four different graph neural network models (MLP, GCN, GraphSage, GAT) across 31 real-world datasets. The rank of each metric based on its correlation with GCN performance is also included, indicating the relative importance of different homophily aspects in predicting model performance.
read the caption
Table 1: Pearson correlation with p-value of all the metrics with model performance of node classification on 31 real-world datasets.
Full paper#



















