Understanding the Gains from Repeated Self-Distillation

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it provides a theoretical understanding of the significant gains achievable through repeated self-distillation, a technique widely used in deep learning but lacking rigorous analysis. It offers practical guidance on hyperparameter selection and opens avenues for optimizing knowledge transfer and model generalization.

Visual Insights

#

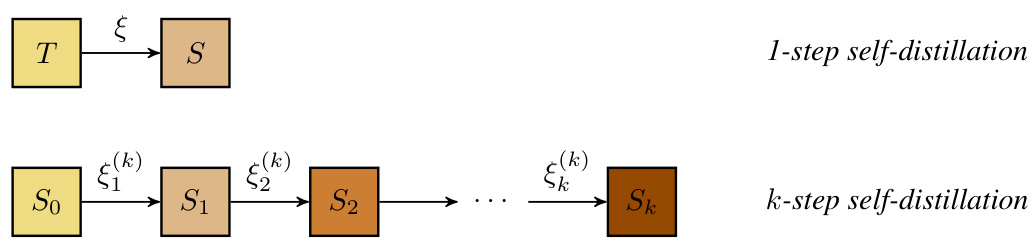
This figure illustrates the difference between 1-step and k-step self-distillation. In 1-step self-distillation, a teacher model (T) is used to train a student model (S) using a combined loss function that considers both the teacher’s prediction and the ground truth label. In k-step self-distillation, this process is repeated k times, where the student model from the previous step acts as the teacher for the next step. The figure shows this process using boxes to represent the models and arrows to represent the training process with parameters ξ.

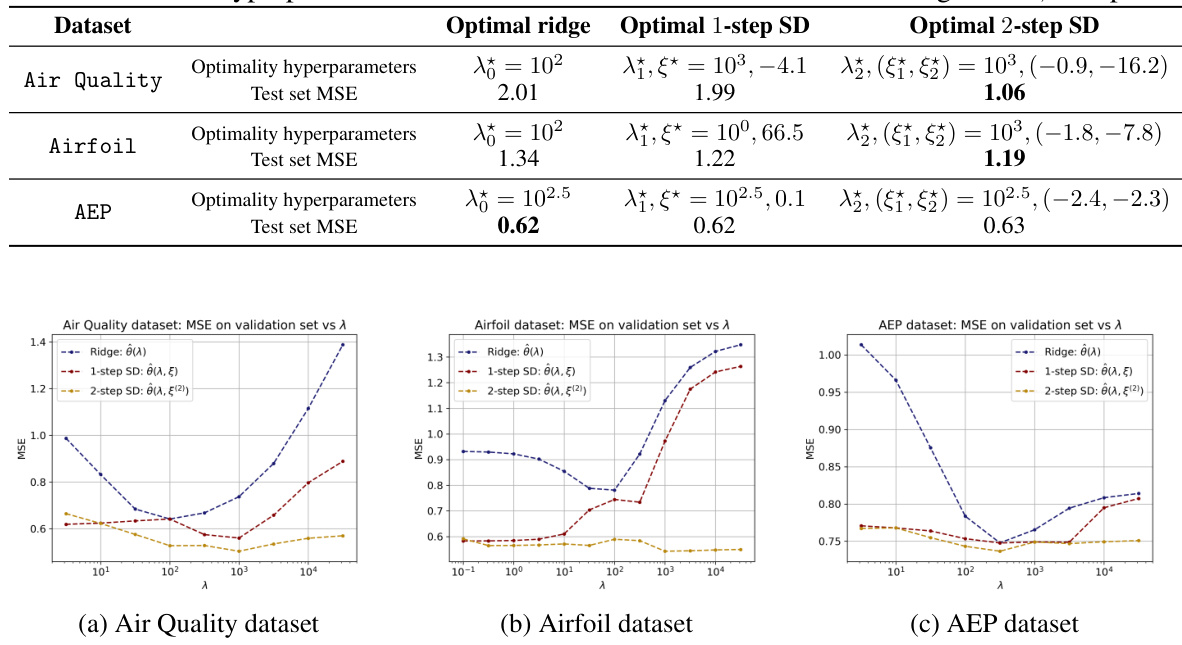
This table presents a comparison of the Mean Squared Error (MSE) achieved by three different regression models on three real-world datasets: Air Quality, Airfoil, and AEP. The models compared are the standard Ridge regression, 1-step Self-Distillation (SD), and 2-step SD. For each model and dataset, the optimal hyperparameters (lambda and the imitation parameters, xi) that minimize the MSE on a validation set are reported, along with the resulting MSE on a held-out test set. The table shows that 2-step SD can sometimes outperform both Ridge regression and 1-step SD, achieving lower test MSE.

In-depth insights

#

Repeated SD Gains

#

The concept of “Repeated SD Gains” in the context of self-distillation suggests that iteratively applying the self-distillation process leads to cumulative improvements in model performance. Unlike traditional knowledge distillation which transfers knowledge from a larger teacher model to a smaller student model, self-distillation uses the same architecture for both teacher and student. The paper’s analysis focuses on the linear regression setting, demonstrating that repeated self-distillation can significantly reduce excess risk, potentially by a factor as large as the input dimension (d). This is achieved by optimizing the imitation parameter at each step. The theoretical findings are supported by empirical results on regression datasets, showing improvements of up to 47%. The key insight is that multi-step self-distillation offers additional freedom in controlling the model’s spectrum, thereby enhancing its generalization capabilities and leading to substantial performance gains beyond what’s achievable with a single step.

Linear Regression

#

The section on linear regression serves as the foundational model for analyzing self-distillation’s impact. The authors strategically choose linear regression due to its simplicity and analytical tractability, making it ideal for theoretical analysis of the core concepts. The use of a fixed design setup, where the input data matrix X is treated as fixed, allows for a clean separation of signal from noise, simplifying the study of bias and variance. This allows for rigorous examination of how multi-step self-distillation impacts the excess risk of the model, particularly when compared to a standard ridge estimator and one-step self-distillation. Key assumptions, such as the uniqueness of singular values and the alignment of the underlying true parameter vector with the data’s eigenbasis, are carefully examined to highlight the conditions under which multi-step self-distillation can significantly improve the estimator’s performance. This theoretical foundation provides valuable insights into the effectiveness of self-distillation as a method for model refinement. The linear regression task is a canonical problem, allowing the researchers to generate clear, mathematically provable results.

Assumption Analysis

#

A rigorous assumption analysis is crucial for validating the theoretical findings of a research paper. It involves a careful examination of the premises upon which the core arguments and claims are built. Identifying the key assumptions allows for a better understanding of the scope and limitations of the study. The analysis should not only list the assumptions but also discuss their plausibility and potential impact on the results. For instance, examining how sensitive the results are to deviations from these assumptions is critical, particularly when dealing with simplified models or real-world applications. The paper should also explore the implications of violating the assumptions, either theoretically or empirically. Addressing edge cases and exploring situations where the assumptions break down helps in a more complete understanding. A solid assumption analysis enhances the reliability and generalizability of the presented research. Providing alternative approaches if certain assumptions are unrealistic or difficult to satisfy is a valuable contribution, enhancing the robustness of the study.

Hyperparameter Choice

#

The choice of hyperparameters is crucial for the success of self-distillation, significantly influencing the model’s performance. The paper investigates the optimal selection of the imitation parameter, ξ, and the regularization parameter, λ, in the context of linear regression. Optimal hyperparameter selection is non-trivial, requiring careful consideration of bias-variance trade-offs and potentially involving computationally intensive searches over a large parameter space. The authors propose a strategy to leverage the theoretical insight that the excess risk is a quadratic function of ξ(k) to more efficiently search for optimal values, reducing the computational burden of a naive grid search, especially for multi-step self-distillation. This demonstrates a practical application of theoretical findings, enabling effective hyperparameter tuning in real-world scenarios. While the theoretical analysis focuses on linear regression, the proposed quadratic optimization approach provides a promising avenue for hyperparameter tuning in more complex models and datasets. The empirical results showcase the effectiveness of this strategy, demonstrating its potential to enhance the performance gains from repeated self-distillation.

Future Work

#

The paper’s theoretical analysis is limited to fixed design linear regression, a significant constraint. Future work should focus on extending the analysis to the more realistic setting of random design regression. This would involve dealing with the complexities introduced by the randomness of the data matrix X. Additionally, the empirical results are limited in scale. Expanding empirical testing to larger, more diverse datasets, and possibly including non-linear regression tasks, would strengthen the findings and demonstrate the practical applicability of the proposed multi-step self-distillation method. A crucial next step is to explore the suggested approach of directly computing optimal parameters through efficient validation set evaluations, which requires further theoretical and empirical investigation. Investigating the sensitivity of the method to hyperparameter choices, particularly the selection of λ and the sequence of ξ values is needed, as current selection methods are heuristic. Finally, examining the method’s behavior in the context of label noise and its potential robustness is a key area for future exploration. A comprehensive study of the method’s generalization performance compared to other knowledge distillation methods, will contribute significantly to its applicability.

More visual insights

#

More on figures

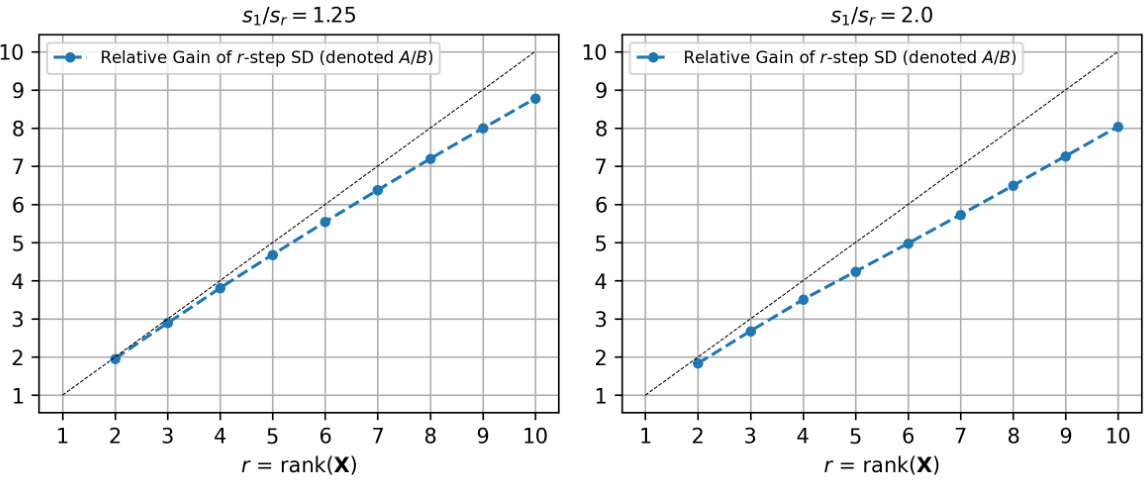
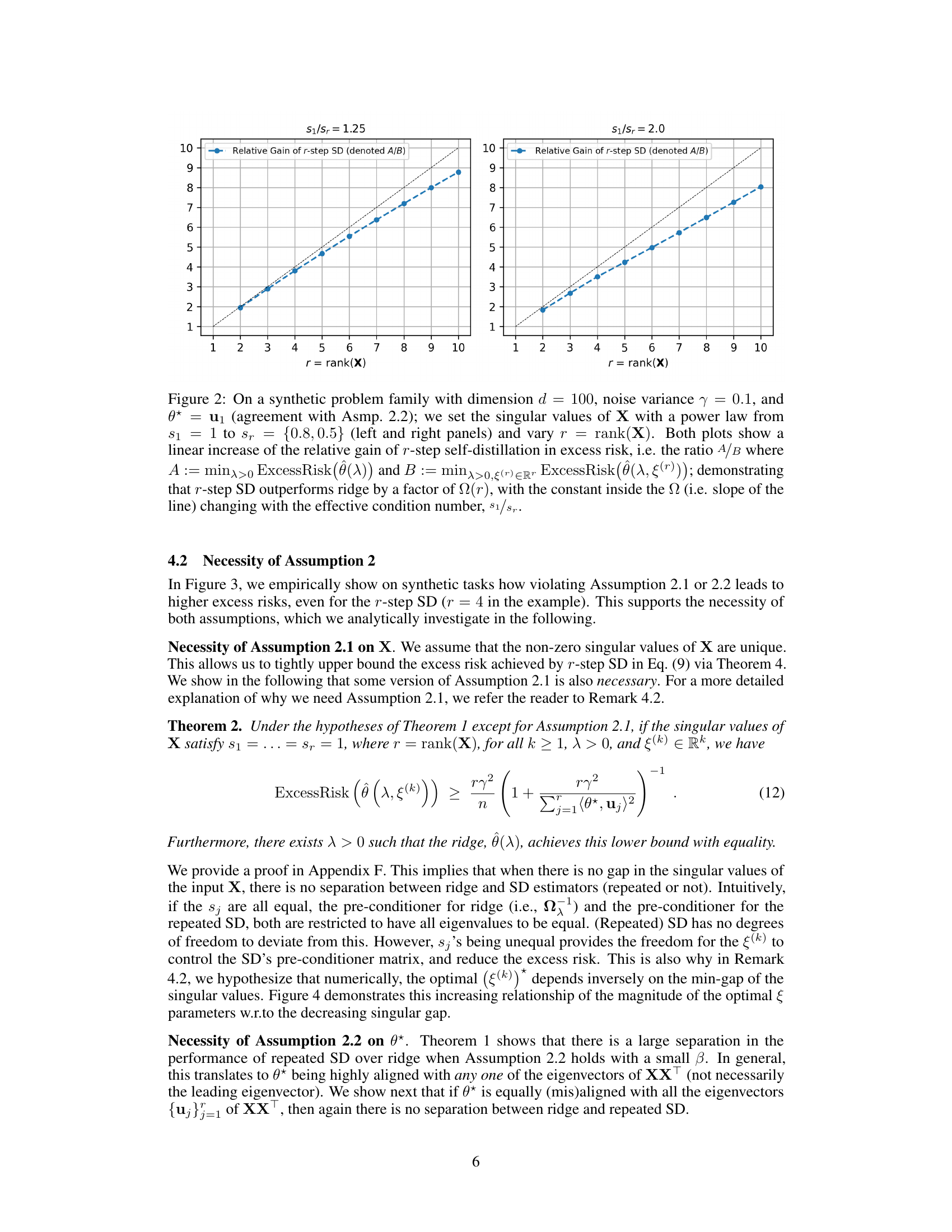
This figure empirically demonstrates the multiplicative separation between the excess risk achieved by r-step self-distillation and the excess risk achieved by 1-step self-distillation and ridge regression, in the context of a synthetic problem family. The plots show that the relative gain in excess risk increases linearly with the rank (r) of the input data matrix (X). This empirically supports Theorem 1 which theoretically proves this multiplicative separation under specific assumptions.

The figure shows the necessity of the assumptions made in Theorem 1. It shows the excess risk of different estimators (ridge, 1-step SD, 2-step SD, 3-step SD, and 4-step SD) for different values of λ and 3 different synthetic datasets. The first dataset satisfies the assumptions, the second violates assumption 2.1, and the third violates assumption 2.2. The results show that the assumptions are necessary for multi-step SD to significantly outperform 1-step SD and ridge.

This figure shows the impact of the singular value gap on the optimal hyperparameter values for different numbers of self-distillation steps. As the gap decreases (i.e., singular values become closer), the magnitude of the optimal hyperparameters increases. This behavior is consistent with Remark 4.2 in the paper, which discusses the necessity of a significant gap between singular values for achieving large performance gains with multi-step self-distillation.

This figure illustrates the difference between 1-step self-distillation and k-step self-distillation. In 1-step self-distillation, a teacher model (T) trains a student model (S) using a combined loss function of teacher predictions and ground truth labels. In k-step self-distillation, this process is repeated k times, where the student model from the previous step becomes the teacher for the next step. Each step introduces an additional hyperparameter ξ(k) which influences the weighting of teacher predictions and ground truth labels in the loss function.

This figure illustrates the difference between 1-step self-distillation and k-step self-distillation. In 1-step self-distillation, a single student model (S) is trained using predictions from a teacher model (T) and ground truth labels. In k-step self-distillation, the process is repeated k times; each time, the student model from the previous step becomes the teacher for the next student model. The parameters ξ and ξ(k) represent the imitation parameter that balances the contributions of teacher predictions and ground truth labels.

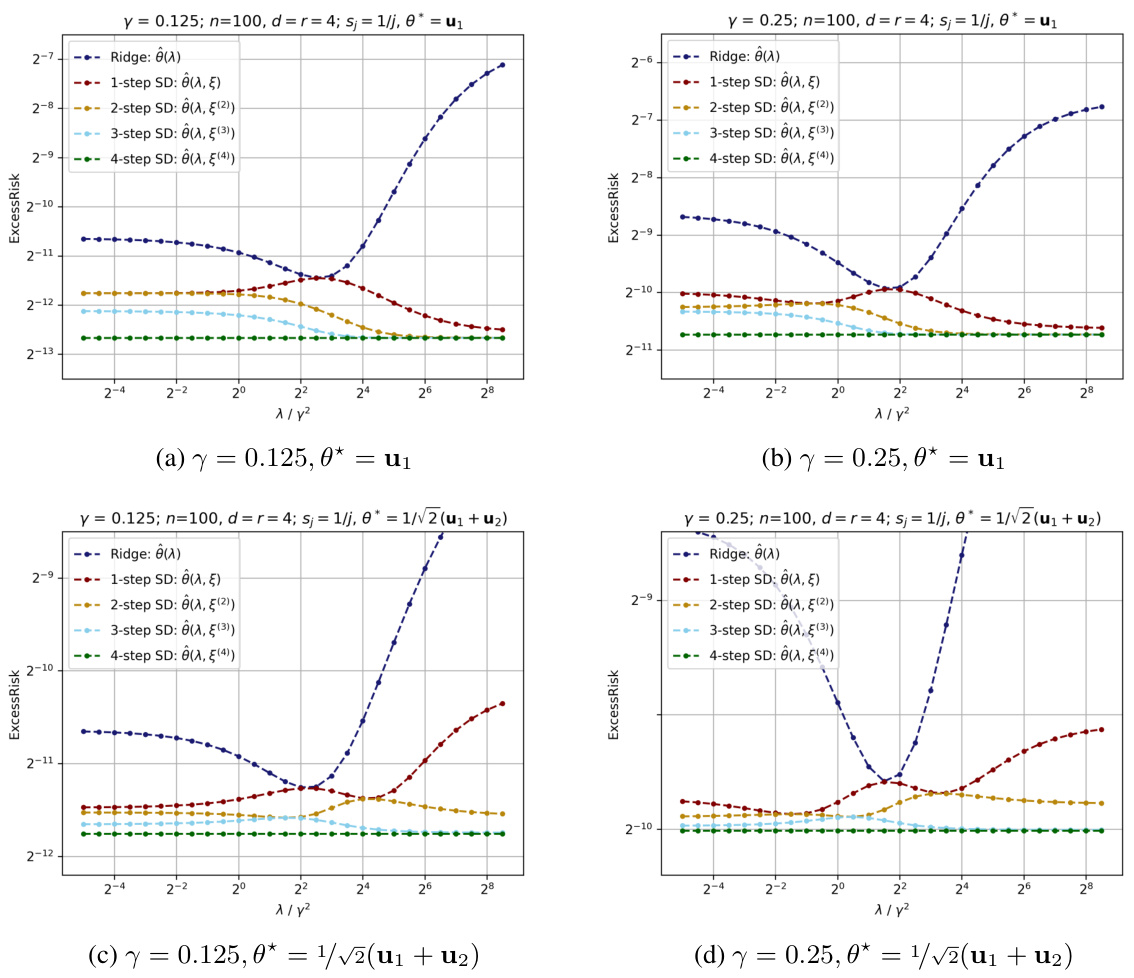
This figure displays the excess risk curves for ridge regression and 1-4 steps of self-distillation for a range of λ values. The curves show how the excess risk changes as the number of steps and the regularization parameter λ are varied. It demonstrates how multi-step self-distillation can reduce the excess risk in linear regression. The figure also validates the necessity of assumptions made earlier in the paper. The two different panels represent different noise levels and different relationships between θ* and the eigenvectors of XXᵀ. The results demonstrate how multi-step SD significantly improves upon the 1-step SD and Ridge regression.

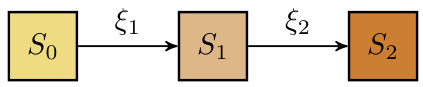
This figure illustrates the difference between one-step self-distillation and k-step self-distillation. In one-step self-distillation, a teacher model (T) trains a student model (S) using a combined loss function of the teacher’s prediction and ground truth. In k-step self-distillation, the process is repeated k times, with the student model from the previous step becoming the teacher for the next step. Each step uses a parameter ξ to weight the influence of the teacher’s prediction and ground truth labels.

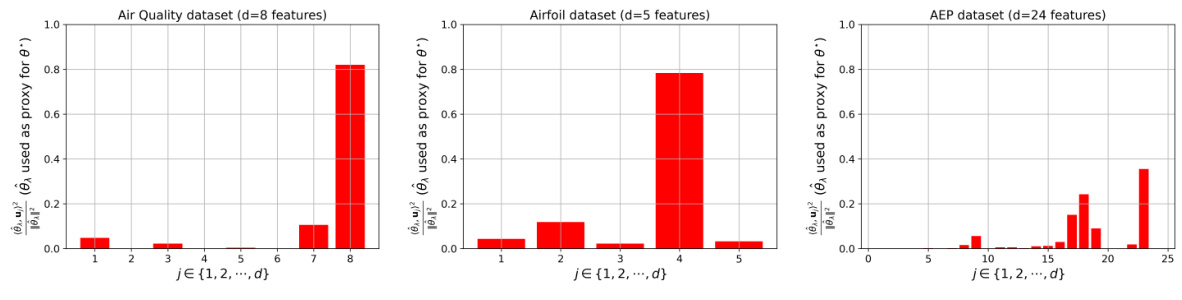
This figure shows the alignment between the true parameter vector θ* and the eigenvectors of the data covariance matrix for three real-world datasets. The height of each bar represents the squared cosine similarity between θ* (approximated by the ridge regression solution) and each eigenvector. For the Air Quality and Airfoil datasets, θ* aligns strongly with a few eigenvectors, indicating that the data contains strong linear relationships that self-distillation can exploit to reduce error. In contrast, for the AEP dataset, θ* does not align strongly with any eigenvector, which explains why self-distillation does not improve the model’s performance.

This figure shows the validation set MSE (mean squared error) plotted against the regularization parameter λ (lambda) for three different estimators: Ridge regression, 1-step self-distillation (SD), and 2-step SD. Each curve represents the performance of a specific estimator across different values of λ. The purpose is to compare the performance of the three estimators on a validation set and to show the effect of repeated self-distillation on model performance, particularly on the test error. By tuning λ and the self-distillation parameters, the 2-step SD aims to achieve lower MSE on the validation set compared to the other estimators, indicating its potential for better generalization.

Full paper

#