TL;DR#
Reinforcement learning from human feedback (RLHF) often relies on human preference rankings which don’t capture the varying strengths of preferences. This inconsistency makes reward modeling complex and leads to suboptimal policies. Previous methods using linear scaling are often insufficient, hindering the learning of versatile reward functions.
This paper introduces a novel adaptive preference loss function, based on DRO, that addresses this issue. By incorporating an adaptive scaling parameter for each pair of preferences, this method enables more flexibility in reward modeling. The loss function is strictly convex and univariate, allowing for efficient optimization. Experiments with robotic control and natural language generation showcase improved policy performance and better alignment between reward function selection and policy optimization, simplifying hyperparameter tuning.
Key Takeaways#
Why does it matter?#
This paper is crucial for RLHF researchers as it tackles the challenge of reward modeling from ambiguous human preference data. Its novel adaptive preference loss function enhances the flexibility and efficiency of reward learning, leading to improved policy performance and easier hyperparameter tuning. This work also highlights the misalignment issue between reward modeling and policy optimization, offering a potential solution and opening avenues for improved alignment in RLHF.
Visual Insights#
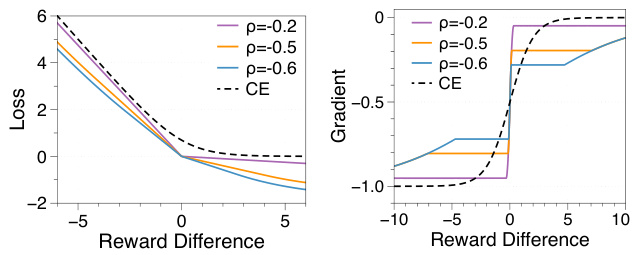
🔼 This figure visualizes the adaptive preference loss function and its gradient. The left panel shows the loss function’s behavior for different values of the reward difference, comparing it to the cross-entropy loss. The right panel shows the gradient of the loss function, highlighting how the adaptive loss function leads to a more flexible reward model by adjusting its sensitivity to reward differences.
read the caption
Figure 1: Visualization of the loss function (left) and its gradient (right) on different reward differences.
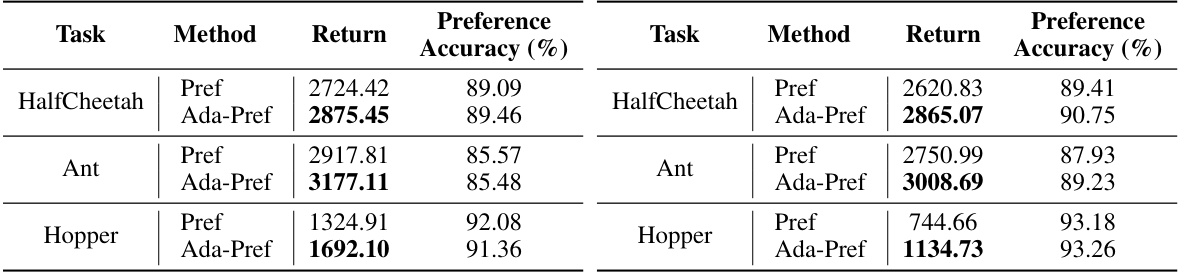
🔼 This table presents the results of the robotic control experiments. For each task (HalfCheetah, Ant, Hopper), it shows the highest return achieved by the best policy found using two different methods: Pref (baseline using cross-entropy loss) and Ada-Pref (the proposed method using adaptive preference scaling). It also provides the average preference prediction accuracy of the corresponding reward function for each method. The data demonstrates the improvement of Ada-Pref over Pref in terms of both policy performance (return) and reward function alignment (accuracy).
read the caption
Table 1: Table for the highest return of the best policy and the average preference prediction accuracy of the corresponding reward function.
In-depth insights#
Adaptive Loss Function#
An adaptive loss function, in the context of reinforcement learning from human feedback (RLHF), is a crucial development addressing the limitations of traditional methods. Standard RLHF often struggles with the inherent ambiguity in human preference data, which typically involves rankings of trajectory segments without explicit strength indicators. An adaptive loss function aims to dynamically adjust its sensitivity to preference strength, assigning higher weights to confident human preferences and lower weights to ambiguous ones. This nuanced approach allows the reward model to learn more effectively from varying degrees of preference certainty, ultimately leading to improved policy alignment and performance. The adaptive nature is typically achieved through instance-specific scaling parameters learned during training, thereby increasing the flexibility and robustness of reward modeling, and mitigating the risk of overfitting or misinterpreting uncertain feedback. The core benefit lies in its ability to better capture the subtle nuances of human preferences, resulting in more robust and effective reward functions, which consequently improve the policy’s performance and alignment with human values. Computational efficiency is often a key consideration in the design and implementation of these adaptive approaches, and usually efficient optimization methods are leveraged to maintain tractability.
DRO-based Reward#
A DRO-based reward approach in reinforcement learning leverages the robustness of distributionally robust optimization. Instead of learning a reward function that performs optimally on the training data’s empirical distribution, DRO aims for a reward function performing well across a range of possible distributions. This is crucial when human feedback, often noisy or inconsistent, shapes reward signals. By incorporating DRO, the method implicitly accounts for the uncertainty inherent in human preferences, creating more robust and generalizable reward models. The key advantage lies in the ability to assign different weights (scaling factors) to various preference pairs depending on their ambiguity or certainty. Ambiguous preferences receive lower weights, preventing overfitting to noisy data, while clear preferences are weighted more heavily, allowing the model to learn effectively from strong signals. This adaptive approach leads to improved policy performance and better alignment between reward function selection and downstream policy optimization, simplifying the hyperparameter tuning process.
RLHF Misalignment#
RLHF, while promising, suffers from a critical challenge: misalignment between reward model optimization and downstream policy optimization. Optimizing solely for reward prediction accuracy (e.g., high preference prediction accuracy) doesn’t guarantee optimal policy performance. This stems from the limitations of preference data, which often lacks the granularity to fully capture nuanced reward differences, leading to inconsistent scaling between preference strength and reward differences. The paper addresses this by proposing an adaptive preference loss, introducing instance-specific scaling parameters to adjust the loss function’s sensitivity based on the ambiguity of each preference comparison. This allows for more flexible reward modeling, leading to better alignment with policy optimization and easing hyperparameter tuning. The core insight is that directly addressing the uncertainty inherent in preference data improves the overall RLHF process, ultimately yielding better policies and avoiding suboptimal reward function selection.
Robotic Control Tests#
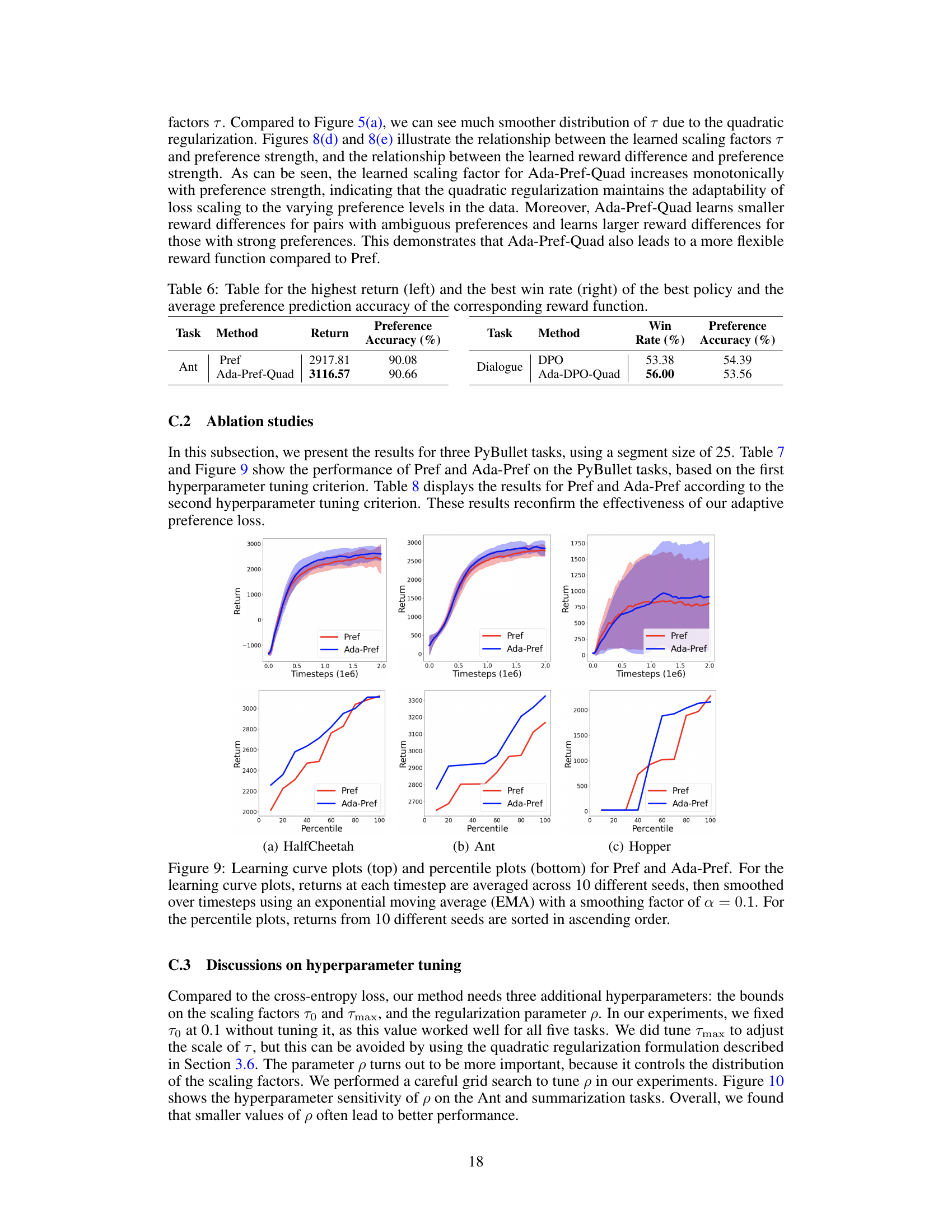
The robotic control experiments section in the paper is crucial for evaluating the effectiveness of the proposed adaptive preference scaling method in reinforcement learning. The researchers leverage a synthetic preference dataset which is generated using ground truth rewards, a clever design choice which avoids the high cost and time involved in collecting human preference data for robotic tasks. They utilize three standard robotic control environments – HalfCheetah, Ant, and Hopper – to ensure broad applicability and comparability to prior work. The experiments are designed to be robust, using multiple random seeds, which gives us greater confidence in the results. Comparing the proposed method to a standard cross-entropy baseline on these tasks allows for clear evaluation of the performance improvements achieved by the adaptive scaling. The focus on both reward function prediction accuracy and the downstream policy performance is a noteworthy aspect of the experimental design, which serves to illuminate the alignment of reward learning with policy optimization. Finally, the detailed analysis of the results, which include learning curves, percentile plots, and statistical measures, suggests a rigorous evaluation of their approach, demonstrating its effectiveness on multiple tasks.
LLM Text Generation#
Large language models (LLMs) are revolutionizing text generation, offering unprecedented capabilities in various applications. Their ability to learn complex patterns and relationships from massive datasets allows for the creation of human-quality text, ranging from creative writing and code generation to summarization and translation. However, the training process of LLMs often involves massive computational resources and datasets. Ethical considerations are paramount, as biases present in training data can easily be reflected in the generated text, potentially leading to unfair or discriminatory outputs. Research into techniques like reinforcement learning from human feedback (RLHF) attempts to mitigate these biases, aligning LLM output more closely with human preferences and values. Despite challenges, the advancements in LLM text generation demonstrate immense potential, promising to reshape communication and content creation across various domains. Future research will likely focus on enhancing efficiency, addressing ethical concerns, and improving controllability over the generated text, ensuring its responsible and beneficial use.
More visual insights#
More on figures

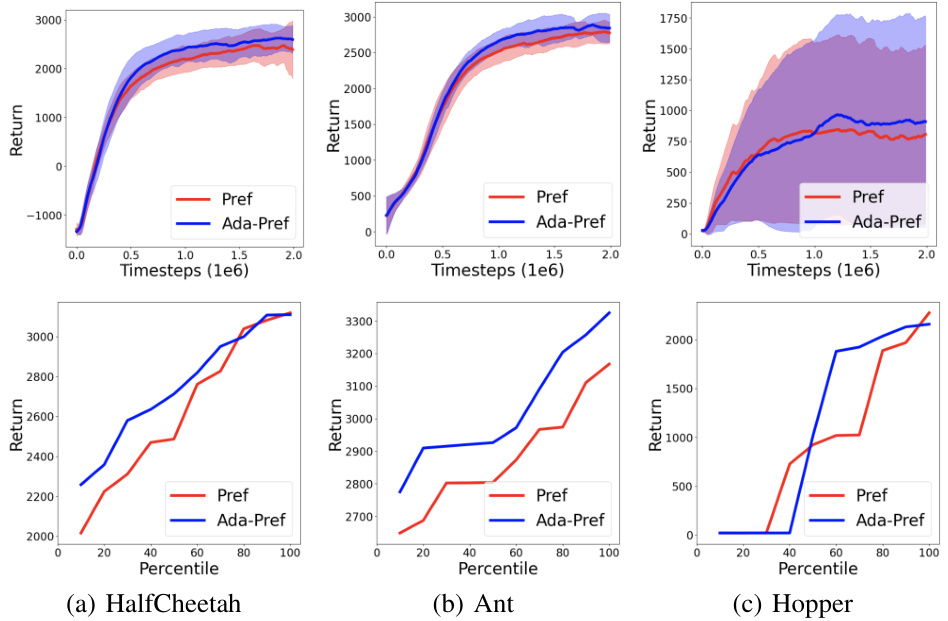
🔼 This figure compares the performance of the baseline method (Pref) and the proposed method (Ada-Pref) across three robotic control tasks. The top row shows learning curves, plotting average returns over time for each method across 10 different random seeds. The bottom row displays percentile plots, providing a more detailed view of performance variability across the 10 seeds. The plots demonstrate Ada-Pref’s consistent superiority over Pref in terms of cumulative returns and robustness.
read the caption
Figure 2: Learning curve plots (top) and percentile plots (bottom) for Pref and Ada-Pref. For the learning curve plots, returns at each timestep are averaged across 10 different seeds, then smoothed over timesteps using an exponential moving average (EMA) with a smoothing factor of α = 0.1. For the percentile plots, returns from 10 different seeds are sorted in ascending order.
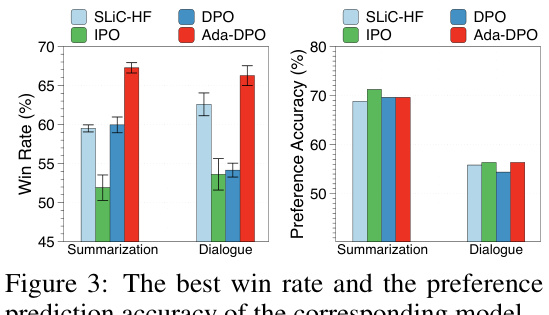
🔼 This figure shows a comparison of different methods (SLIC-HF, IPO, DPO, and Ada-DPO) for two natural language generation tasks: summarization and dialogue. For each method, the figure displays the highest win rate achieved (percentage of times the method’s generated response was preferred over a baseline) and the corresponding preference prediction accuracy. The goal is to demonstrate the improved performance of the Ada-DPO method.
read the caption
Figure 3: The best win rate and the preference prediction accuracy of the corresponding model
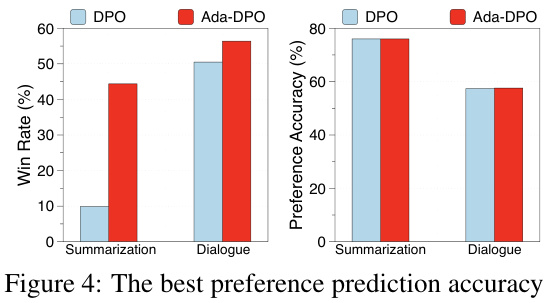
🔼 This figure compares the performance of DPO and Ada-DPO methods across summarization and dialogue tasks, showing the best preference prediction accuracy achieved by each method for each task. Ada-DPO demonstrates a better ability to align the learned reward function with policy optimization, leading to higher win rates (performance against baseline models) than the standard DPO method. Note that the preference accuracy reported is the performance of the model chosen for its best accuracy, rather than its win rate.
read the caption
Figure 4: The best preference prediction accuracy
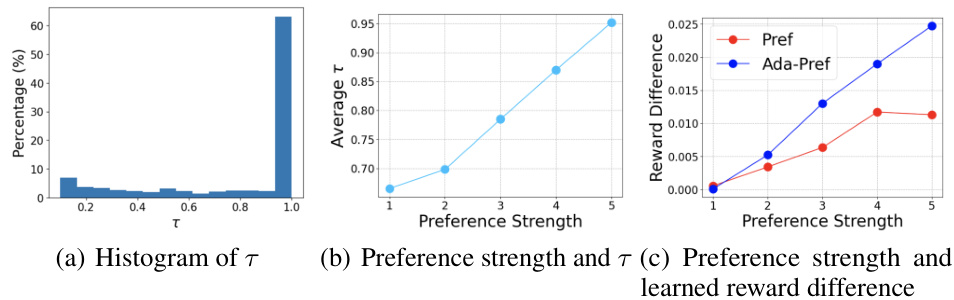
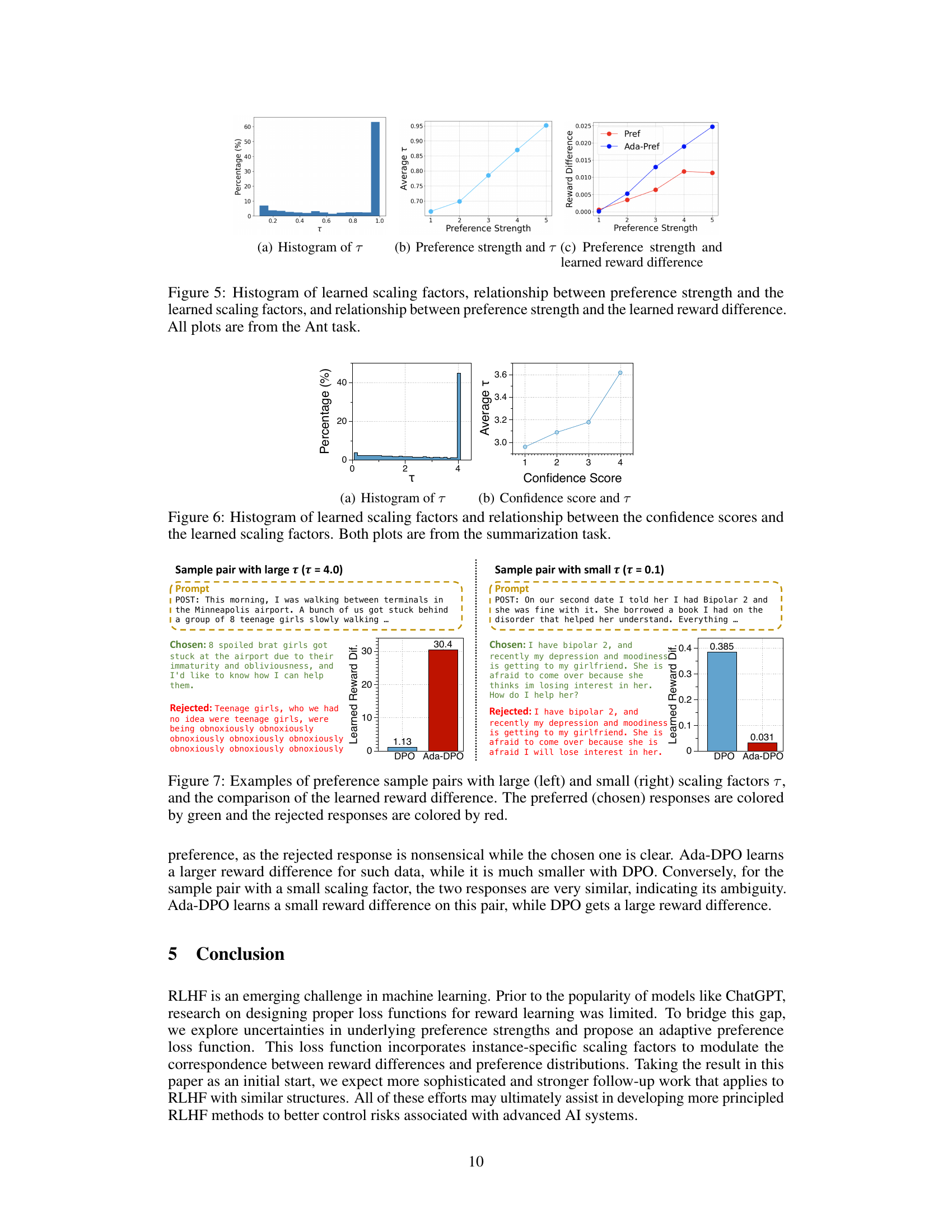
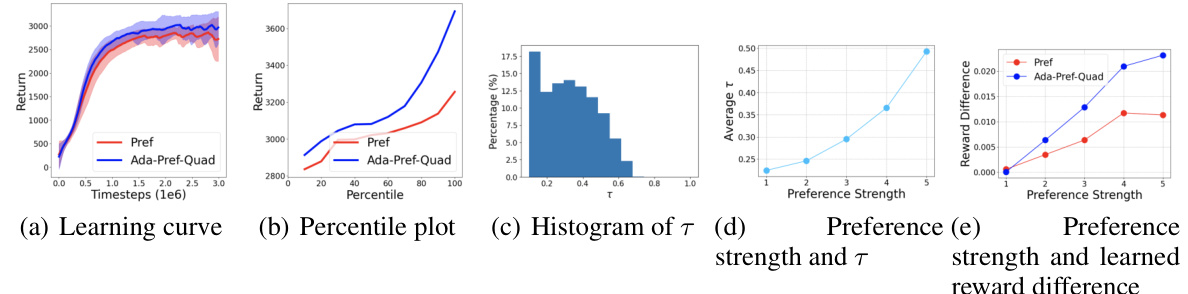
🔼 This figure consists of three subplots visualizing different aspects of the adaptive preference scaling method applied to the Ant robotic control task. (a) shows a histogram of the learned scaling factors (τ), demonstrating the distribution of the learned scaling parameters across different instances. (b) illustrates the relationship between preference strength (measured by the true reward difference) and the average learned scaling factor, showing how the scaling factor adapts to varying levels of preference uncertainty. Lastly, (c) shows the relationship between preference strength and the learned reward difference for both the proposed Ada-Pref method and the baseline Pref method. This comparison visually demonstrates Ada-Pref’s adaptability, learning larger reward differences for strong preferences and smaller differences for ambiguous ones.
read the caption
Figure 5: Histogram of learned scaling factors, relationship between preference strength and the learned scaling factors, and relationship between preference strength and the learned reward difference. All plots are from the Ant task.

🔼 This figure visualizes the distribution of learned scaling factors (τ) and their relationship with confidence scores in the summarization task. The left panel shows a histogram of the scaling factors, indicating their distribution across different values. The right panel presents a line graph showing how the average scaling factor changes as the confidence score increases. This suggests that higher confidence scores (indicating clearer preferences) are associated with larger scaling factors, while lower confidence scores (indicating ambiguous preferences) are linked to smaller scaling factors.
read the caption
Figure 6: Histogram of learned scaling factors and relationship between the confidence scores and the learned scaling factors. Both plots are from the summarization task.
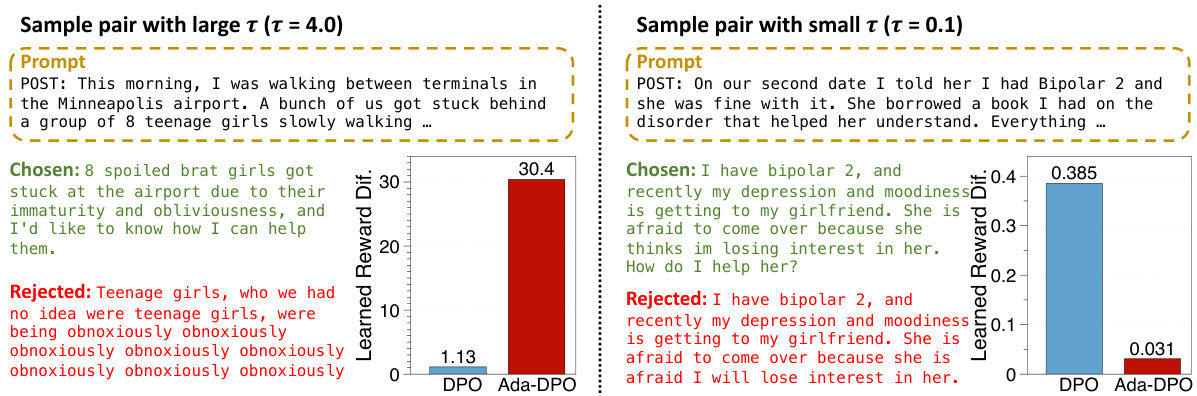
🔼 This figure shows two examples of preference data used in the paper. The left example demonstrates a pair with a large scaling factor (τ = 4.0). The chosen response is rated as significantly better than the rejected response, leading to a large reward difference learned by the Ada-DPO method. The right example shows a pair with a small scaling factor (τ = 0.1). Here, the two responses are very similar, resulting in a small reward difference learned by Ada-DPO, signifying that the method is successfully adapting the loss scaling to the varying preference levels in the data. The figure helps to illustrate how the adaptive preference scaling adjusts the sensitivity of the model to varying degrees of preference strength.
read the caption
Figure 7: Examples of preference sample pairs with large (left) and small (right) scaling factors τ, and the comparison of the learned reward difference. The preferred (chosen) responses are colored by green and the rejected responses are colored by red.

🔼 This figure shows the performance of two reward learning methods, Pref and Ada-Pref, on three robotic control tasks. The top part displays learning curves, showing the average return over time for each method. The bottom part shows percentile plots, illustrating the distribution of returns across multiple independent runs. Ada-Pref consistently outperforms Pref across all tasks and percentiles.
read the caption
Figure 2: Learning curve plots (top) and percentile plots (bottom) for Pref and Ada-Pref. For the learning curve plots, returns at each timestep are averaged across 10 different seeds, then smoothed over timesteps using an exponential moving average (EMA) with a smoothing factor of α = 0.1. For the percentile plots, returns from 10 different seeds are sorted in ascending order.

🔼 This figure compares the performance of the proposed Ada-Pref method and the baseline Pref method across three robotic control tasks (HalfCheetah, Ant, and Hopper). The top row shows the learning curves for both methods, where the average return is plotted against the number of timesteps. The bottom row shows the percentile plots, which display the distribution of returns across multiple trials. The figure demonstrates that Ada-Pref consistently outperforms Pref in terms of both average return and percentile performance across all three tasks.
read the caption
Figure 2: Learning curve plots (top) and percentile plots (bottom) for Pref and Ada-Pref. For the learning curve plots, returns at each timestep are averaged across 10 different seeds, then smoothed over timesteps using an exponential moving average (EMA) with a smoothing factor of α = 0.1. For the percentile plots, returns from 10 different seeds are sorted in ascending order.
🔼 This figure presents a comprehensive analysis of the Ant task, comparing the performance of Pref and Ada-Pref-Quad. It includes four sub-figures. (a) shows the learning curves, illustrating the performance improvement of Ada-Pref-Quad over Pref across time steps. (b) displays percentile plots, demonstrating the consistent superiority of Ada-Pref-Quad across different random seeds. (c) provides a histogram of the learned scaling factors (τ), visualizing their distribution. Finally, (d) and (e) illustrate the relationship between preference strength and both the learned scaling factor and the resulting reward difference, highlighting how Ada-Pref-Quad adapts to varying preference strengths more effectively than Pref.
read the caption
Figure 8: Left: Learning curve and percentile plot for Pref and Ada-Pref-Quad. Middle: Histogram of the learned scaling factors. Right: Relationship between preference strength and the learned scaling factors, and relationship between preference strength and the learned reward difference. All plots are from the Ant task.
🔼 This figure shows the performance comparison between the baseline method (Pref) and the proposed adaptive preference scaling method (Ada-Pref) on three robotic control tasks. The top row presents learning curves, illustrating the average return over time for each method across multiple trials. The bottom row displays percentile plots, showing the distribution of returns across different trials for each method and providing a more robust measure of performance. Ada-Pref consistently outperforms Pref across all tasks and percentiles.
read the caption
Figure 2: Learning curve plots (top) and percentile plots (bottom) for Pref and Ada-Pref. For the learning curve plots, returns at each timestep are averaged across 10 different seeds, then smoothed over timesteps using an exponential moving average (EMA) with a smoothing factor of α = 0.1. For the percentile plots, returns from 10 different seeds are sorted in ascending order.
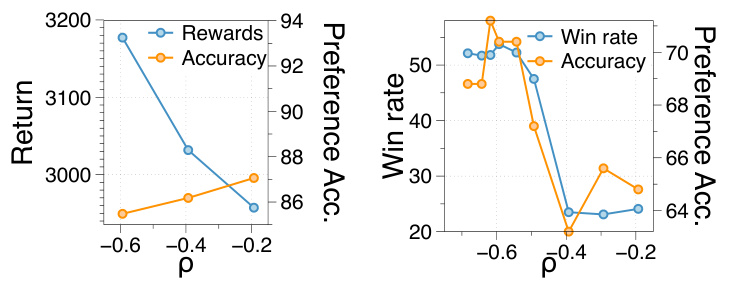
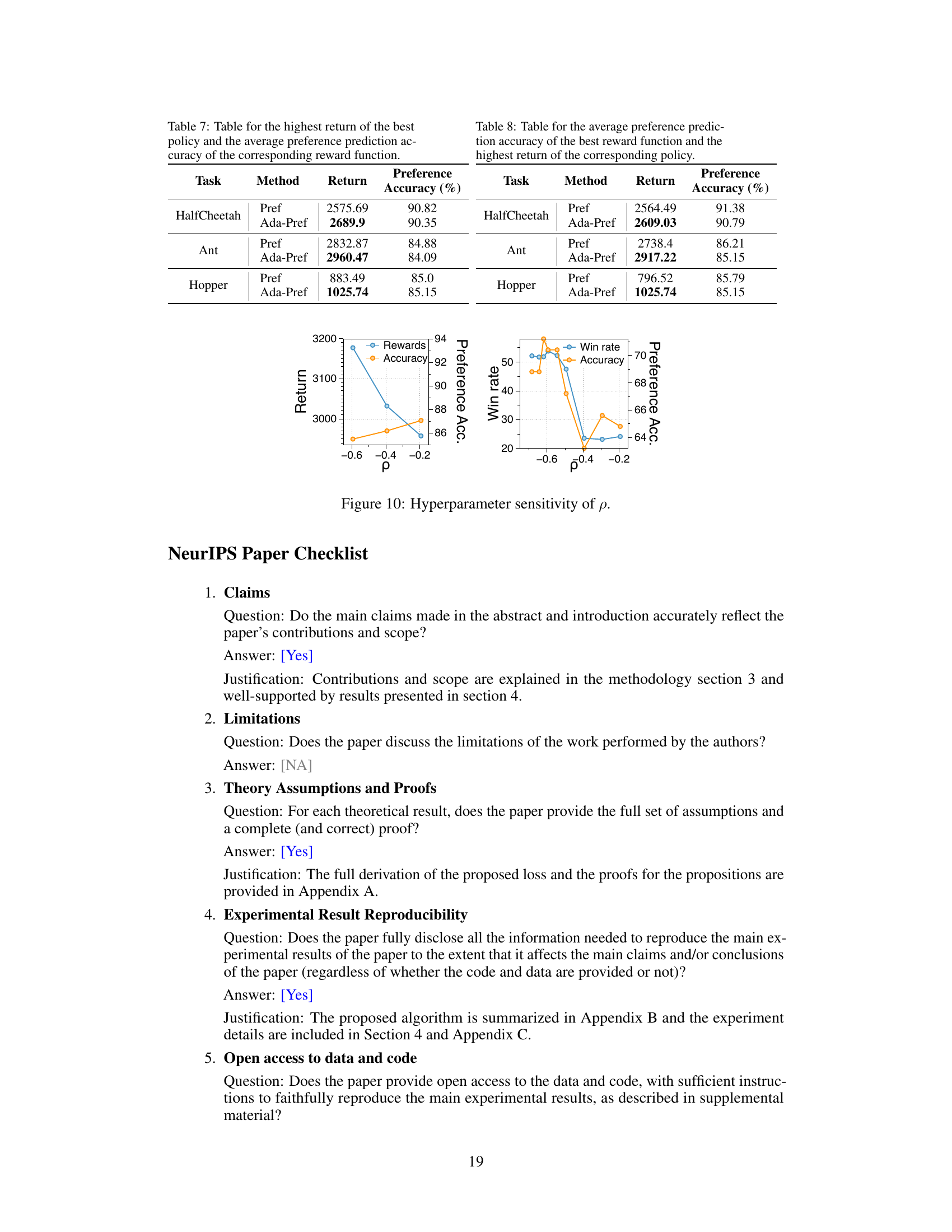
🔼 This figure shows the impact of the hyperparameter ρ on the performance of the model in terms of rewards and win rate. The left plot shows the relationship between ρ and the average return achieved by the model. The right plot shows the relationship between ρ and the win rate, reflecting the model’s ability to correctly predict human preferences. The plots demonstrate that there is an optimal range for ρ, outside which performance decreases.
read the caption
Figure 10: Hyperparameter sensitivity of ρ.
More on tables

🔼 This table lists the hyperparameters used for reward learning when obtaining the results shown in Table 1. The hyperparameters shown are for the Pref and Ada-Pref methods across three different robotic control tasks (HalfCheetah, Ant, and Hopper) from the PyBullet environment. The values represent the number of epochs, learning rate, T_max (maximum scaling factor), and ρ_0 (KL constraint parameter).
read the caption
Table 3: Chosen hyperparameters for reward learning used for Table 1.
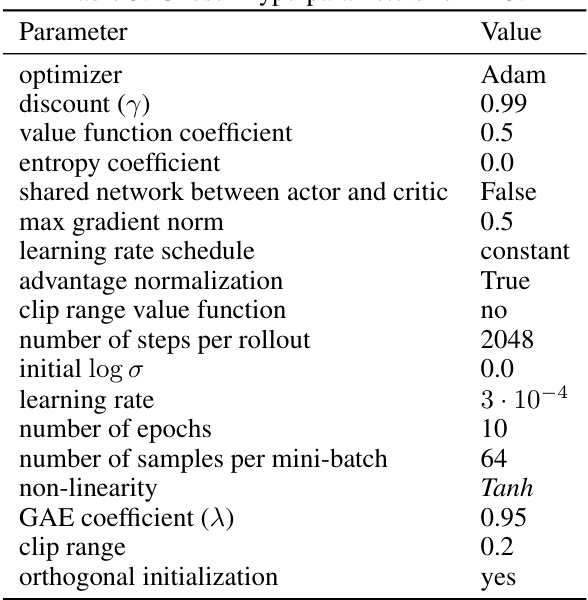
🔼 This table lists the hyperparameters used for the Proximal Policy Optimization (PPO) algorithm in the robotic control experiments. It specifies settings for the optimizer, discount factor, value function coefficient, entropy coefficient, gradient norm, learning rate schedule, advantage normalization, clip range for the value function, number of steps per rollout, initial log standard deviation, learning rate, number of epochs, mini-batch size, non-linearity, generalized advantage estimation (GAE) coefficient, clip range, and orthogonal initialization.
read the caption
Table 5: Chosen hyperparameters for PPO.

🔼 This table presents the results of the Ant and Dialogue tasks. For the Ant task, it shows the return and preference accuracy for Pref and Ada-Pref-Quad. For the Dialogue task, it shows the win rate and preference accuracy for DPO and Ada-DPO-Quad. It summarizes the performance of the best policies and their corresponding reward functions based on two different evaluation metrics (return and win rate).
read the caption
Table 6: Table for the highest return (left) and the best win rate (right) of the best policy and the average preference prediction accuracy of the corresponding reward function.
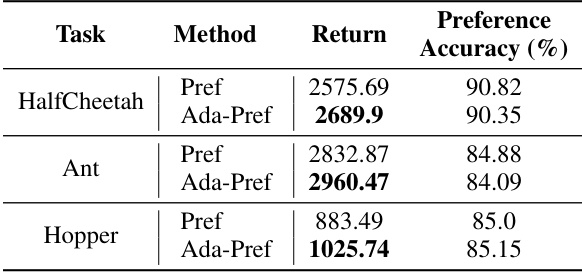
🔼 This table presents the results of the Pref and Ada-Pref methods on three robotic control tasks (HalfCheetah, Ant, and Hopper). For each task, it shows the highest return achieved by the policy and the average preference prediction accuracy of the corresponding reward function. The table allows comparison of the performance of the standard cross-entropy loss method (Pref) against the proposed adaptive preference scaling method (Ada-Pref).
read the caption
Table 7: Table for the highest return of the best policy and the average preference prediction accuracy of the corresponding reward function.
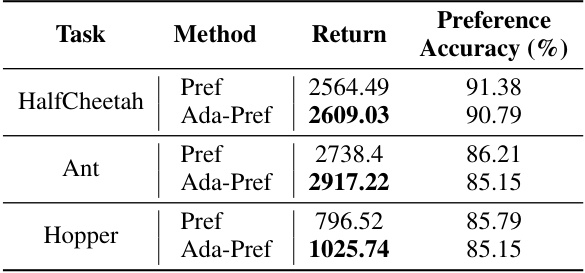
🔼 This table presents the results of the experiments using the second hyperparameter tuning criterion. The table shows the average preference prediction accuracy of the best reward function (selected based on accuracy) and the highest return achieved by the corresponding policy for the HalfCheetah, Ant, and Hopper robotic control tasks using both the Pref (baseline) and Ada-Pref methods. It highlights the performance trade-off when prioritizing reward function accuracy over overall policy performance.
read the caption
Table 8: Table for the average preference prediction accuracy of the best reward function and the highest return of the corresponding policy.
Full paper#