TL;DR#
Representing sets while preserving user privacy is a challenge in data analysis. Existing methods, like those based on private histograms, often suffer from high error rates or require excessive space. The limitations of non-private solutions such as Bloom filters, compounded by noise injection methods, are also significant. This necessitates more efficient and privacy-preserving techniques.
The research introduces novel algorithms using a unique approach that embeds sets into random linear systems, avoiding the limitations of noise-injection methods. This approach yields differentially private set representations with error probabilities matching randomized response (even up to constants). The results not only show optimal privacy-utility trade-offs and space usage but also demonstrate exponentially smaller error than competing private histogram methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and data structures. It presents novel, efficient algorithms for representing sets privately, bridging a gap in existing research and offering significant improvements in privacy-utility trade-offs. The work also establishes new lower bounds, demonstrating the optimality of the proposed techniques and suggesting directions for future research in this active area of computer science.
Visual Insights#
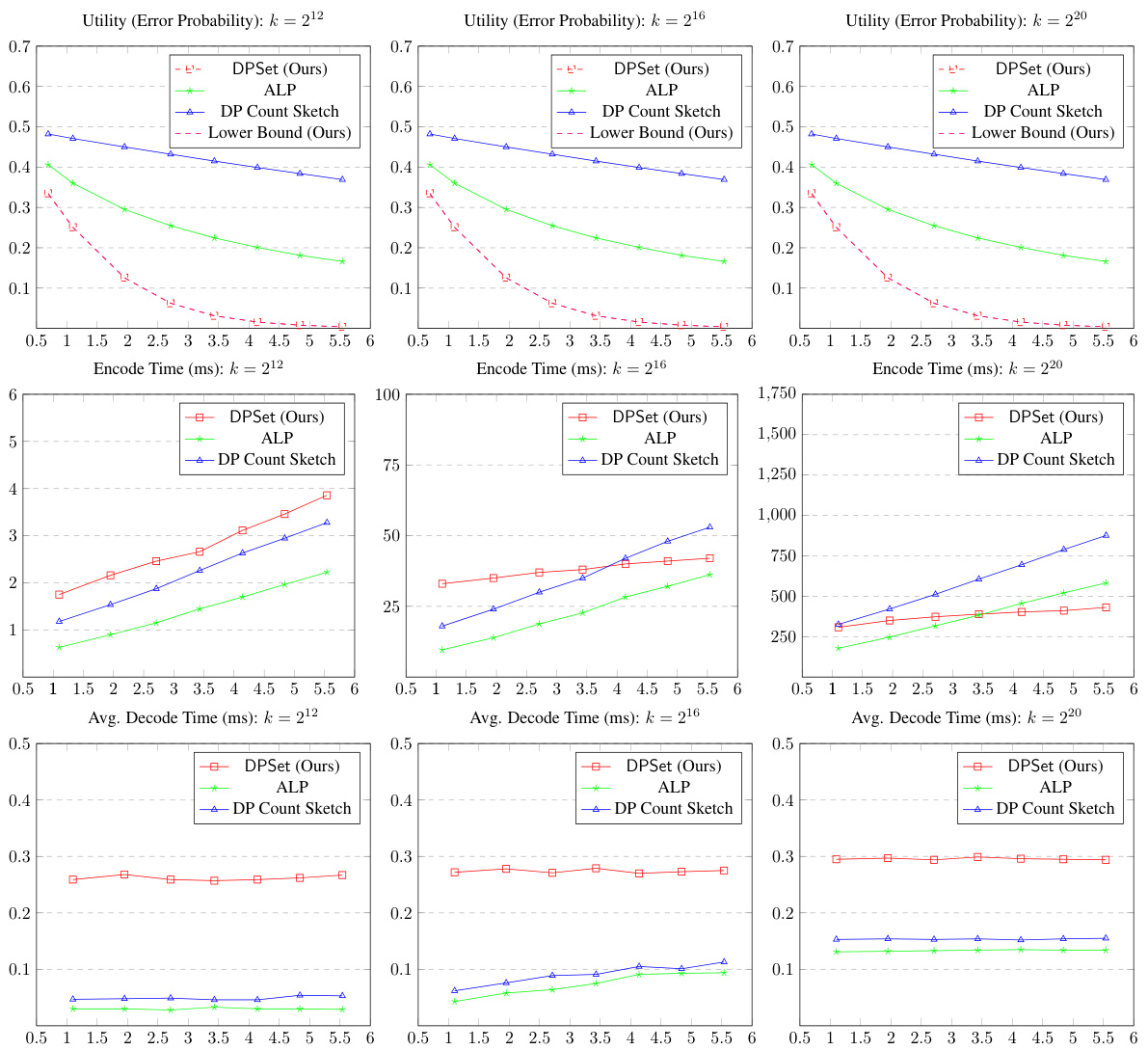
🔼 This figure compares the performance of three differentially private set mechanisms: DPSet (the proposed method), ALP, and DP Count Sketch. It shows the trade-off between privacy (epsilon, the x-axis) and utility (error probability, encoding time, and decoding time, the y-axis). The results are presented for three different set sizes (k = 212, 216, 220) and demonstrate DPSet’s superior utility across all metrics, particularly in terms of significantly lower error probability than competing methods.
read the caption
Figure 1: Comparisons of of DPSet, ALP, and DP Count Sketch with δ < 2-40. The x-axis is privacy parameter e and the y-axis is error probability, encoding time (ms) or decoding time (ms).

🔼 The figure compares the performance of three different differentially private set mechanisms: DPSet (the authors’ proposed method), ALP, and DP Count Sketch. It shows how error probability, encoding time, and decoding time vary with the privacy parameter (epsilon). The results demonstrate that DPSet achieves significantly lower error probability than the other two methods, while maintaining reasonable encoding and decoding times.
read the caption
Figure 1: Comparisons of of DPSet, ALP, and DP Count Sketch with δ < 2-40. The x-axis is privacy parameter e and the y-axis is error probability, encoding time (ms) or decoding time (ms).
In-depth insights#
DP Set Encoding#
Differentially private (DP) set encoding tackles the challenge of representing sets from a large universe while preserving privacy. The core problem involves creating a compact and efficient encoding that allows for querying membership while adhering to DP guarantees. Existing approaches often rely on perturbing non-private representations with noise, but this can lead to suboptimal accuracy. This paper explores a novel approach embedding sets into random linear systems, which provides theoretically optimal trade-offs between privacy and utility, matched by space lower bounds. The key innovation lies in deviating from traditional noise-injection methods, offering significant improvements in error probability. While practical implementation details are important (considerations around hash functions, field size selection), the theoretical foundation promises more efficient and accurate DP set representations than existing methods, with potential applications in various privacy-sensitive domains.
Linear System Embed#
The core idea of “Linear System Embed” revolves around representing sets as solutions to carefully constructed linear systems. This approach offers a powerful alternative to traditional methods that inject noise into non-private set representations. By embedding sets within a random linear system, the technique leverages the inherent structure to distinguish set members from non-members probabilistically. This probabilistic separation is key to achieving differential privacy, as it introduces uncertainty without explicitly adding noise to each data point. The effectiveness hinges on the properties of the chosen linear system and the associated algorithms for encoding and decoding, influencing efficiency and privacy guarantees. Optimal selection of the underlying linear system and parameters is crucial to balance privacy-utility tradeoffs. The framework’s generality allows flexibility in choosing a linear system best suited for specific applications. This embedding approach offers potential advantages in terms of space efficiency and error probability.
Privacy-Utility Tradeoffs#
The core of differentially private (DP) mechanism design lies in balancing privacy preservation with the utility of released information. Privacy-utility tradeoffs explore this fundamental tension. Stronger privacy guarantees (smaller epsilon and delta) typically lead to less useful results (higher error rates, less accurate models), while maximizing utility often compromises privacy. The paper’s analysis of privacy-utility tradeoffs is crucial in establishing the optimality of its proposed constructions. By matching theoretical lower bounds, it demonstrates that the algorithms achieve a near-optimal balance. The tradeoff is not merely asymptotic—the study goes beyond big-O notation and carefully considers constant factors, showing precise matching with the lower bounds. This precision in analyzing the tradeoffs underscores the practical relevance of the findings, moving beyond theoretical statements to provide a concrete understanding of the achievable balance between privacy and utility for representing private sets.
Space Lower Bounds#
The section on “Space Lower Bounds” would rigorously establish the minimum amount of space required to represent a set of size k from a universe U while satisfying differential privacy constraints. This would involve proving a theoretical lower bound on the number of bits needed, showing that no differentially private algorithm can achieve better space efficiency. The proof would likely use information-theoretic arguments, possibly employing techniques like compression arguments or communication complexity, to demonstrate that achieving a certain level of accuracy with specified privacy parameters necessitates a certain minimum space usage. The analysis would be crucial in demonstrating the optimality (or near-optimality) of the proposed algorithms in terms of space efficiency. A key aspect would be the exploration of the trade-off between space and utility (error probability): a tighter lower bound would indicate a stronger result, highlighting the practical implications of the theoretical findings. The lower bound would likely be expressed as a function of k, ε (privacy parameter), and δ (failure probability), providing quantitative insight into the fundamental limits of privacy-preserving set representation.
Future Work#
The paper’s ‘Future Work’ section could explore several promising avenues. Extending the framework to handle non-uniform data distributions is crucial for real-world applicability. While the current work focuses on uniform distributions, many real-world datasets exhibit skewed distributions. Addressing this limitation would significantly broaden the practical impact of the proposed techniques. Another important direction is investigating the trade-offs between privacy, utility, and encoding size more rigorously. The paper establishes theoretical lower bounds, but further analysis, particularly in non-asymptotic regimes, could refine the understanding of these complex relationships. Furthermore, developing more efficient algorithms for larger datasets is a key challenge. The computational complexity of existing methods might hinder scalability when dealing with massive datasets. Finally, exploring alternative linear systems for set representation could unlock further efficiency gains or robustness properties. The authors have demonstrated a successful approach using random band matrices; however, other linear systems may offer advantages in specific scenarios. This is vital for improving the overall performance of this new, efficient differentially private set representation method.
More visual insights#
More on tables

🔼 This figure compares the performance of three differentially private set mechanisms: DPSet (the proposed method), ALP, and DP Count Sketch. It shows the trade-off between privacy (ε) and utility (error probability, encoding time, and decoding time) for different set sizes (k = 2¹², 2¹⁶, 2²⁰). The results demonstrate that DPSet achieves significantly lower error probabilities while maintaining comparable or better efficiency in terms of encoding and decoding times compared to the other methods.
read the caption
Figure 1: Comparisons of of DPSet, ALP, and DP Count Sketch with δ < 2⁻⁴⁰. The x-axis is privacy parameter ε and the y-axis is error probability, encoding time (ms) or decoding time (ms).

🔼 This figure compares the performance of three differentially private set mechanisms: DPSet (the proposed method), ALP, and DP Count Sketch. The plots show the error probability, encoding time, and decoding time for different values of the privacy parameter epsilon (ε), with delta (δ) set to less than 2⁻⁴⁰. It demonstrates the trade-off between privacy (ε), utility (error probability), and efficiency (time).
read the caption
Figure 1: Comparisons of of DPSet, ALP, and DP Count Sketch with δ < 2⁻⁴⁰. The x-axis is privacy parameter ε and the y-axis is error probability, encoding time (ms) or decoding time (ms).
Full paper#



















