TL;DR#
Many machine learning models struggle with domain adaptation, particularly when facing diverse domain shifts. Existing methods often simplify the representation of domain-specific characteristics, limiting their effectiveness. This paper addresses this limitation by proposing a novel Bayesian framework for domain adaptation.
The proposed algorithm, GMDI, utilizes a Gaussian Mixture Model to represent domain indices, allowing for more flexible and accurate modeling of domain-specific information. GMDI dynamically adjusts the mixture components using a Chinese Restaurant Process, enhancing its ability to adapt to various domain shifts. The results demonstrate that GMDI significantly outperforms existing approaches on various benchmark datasets, achieving substantial improvements in both classification and regression tasks.
Key Takeaways#
Why does it matter?#
This paper is significant because it addresses a critical challenge in domain adaptation: handling diverse domain shifts effectively. The proposed method, GMDI, provides a novel way to model domain indices using Gaussian Mixture Models, leading to improved adaptation performance and better theoretical understanding. This opens new avenues for researchers working on improving the robustness and generalization capabilities of machine learning models across various domains.
Visual Insights#
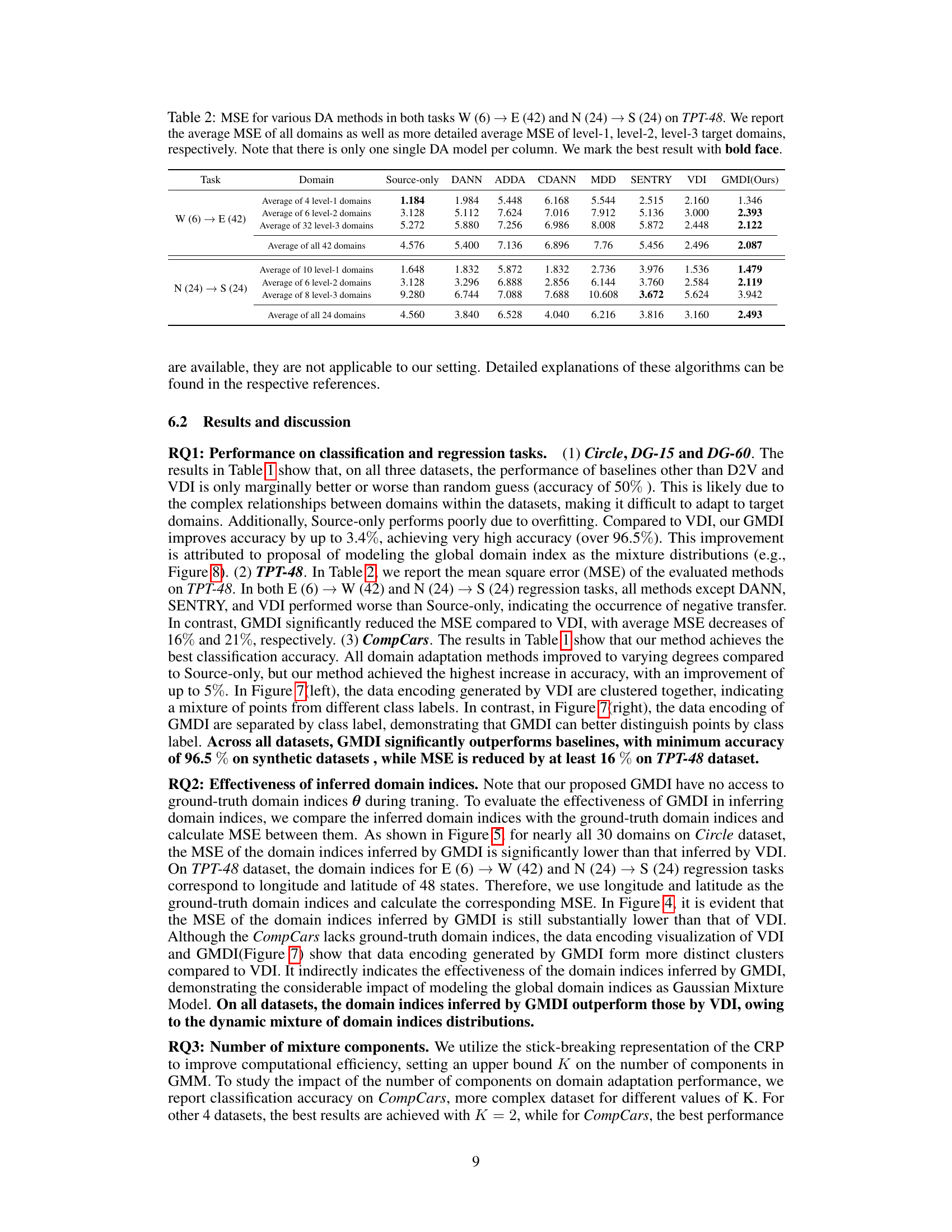
🔼 The figure illustrates how a Gaussian Mixture Model (GMM) better fits the distribution of domain indices compared to a single Gaussian distribution. The green dashed line represents the ground truth distribution of domain indices, showing distinct clusters. The blue line shows a single Gaussian distribution attempting to model this data, failing to capture the multi-modal nature of the data. The red line demonstrates a GMM, which successfully models the distinct clusters in the ground truth distribution. This highlights the advantage of using a GMM to represent the domain indices, as it captures the inherent structure within the data more effectively than a simple Gaussian.
read the caption
Figure 1: Illustration of domain indices modeled by different distributions.
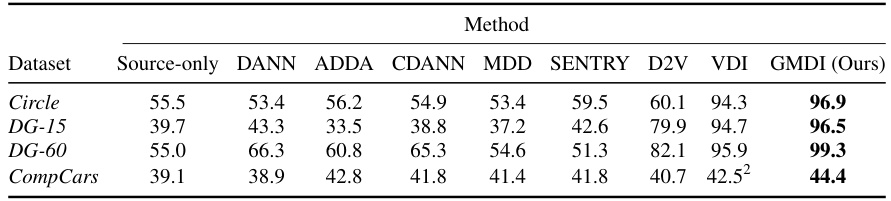
🔼 This table presents the accuracy results of different domain adaptation methods on four classification datasets: Circle (binary), DG-15 (binary), DG-60 (binary), and CompCars (4-way). It compares the performance of GMDI (the proposed method) against several state-of-the-art methods (DANN, ADDA, CDANN, MDD, SENTRY, D2V, VDI) and a source-only baseline. The results demonstrate GMDI’s superior performance in most cases.
read the caption
Table 1: Accuracy on binary classification tasks (Circle, DG-15, and DG-60) and 4-way classification task (CompCars).
In-depth insights#
GMDI: Core Concept#
The core concept of GMDI centers on addressing the limitations of existing domain adaptation methods that model domain indices using a simplistic Gaussian distribution. GMDI innovates by employing a Gaussian Mixture Model (GMM) to represent domain indices, capturing the inherent structure and diversity among different domains more effectively. This dynamic GMM is further enhanced by a Chinese Restaurant Process (CRP) to adaptively determine the optimal number of Gaussian components, ensuring the model’s flexibility to handle varying degrees of domain shift. The resulting richer representation of domain indices leads to more accurate inference and superior domain adaptation performance, surpassing state-of-the-art methods in both classification and regression tasks. A key theoretical advantage is GMDI’s tighter evidence lower bound, ensuring a more robust and interpretable learning process.
Mixture Model: Theory#
A theoretical investigation into mixture models would delve into the underlying assumptions and mathematical properties. Key areas would include exploring the identifiability of parameters, the conditions under which a unique solution exists, and the development of algorithms for parameter estimation. Convergence properties of Expectation-Maximization (EM) and Variational Inference (VI) methods, common for mixture model fitting, are also critical. Analyzing the model selection criteria like AIC and BIC to determine optimal model complexity (number of components) is another key aspect. Furthermore, a theoretical exploration would likely analyze the bias-variance tradeoff within the context of mixture models, highlighting how the number of components and the data affect the model’s ability to generalize to unseen data. Finally, a formal treatment of mixture models should touch upon their relationship to other statistical models and investigate the robustness of mixture model estimations against outliers and model misspecification.
Adaptive Domain Index#
An adaptive domain index is a crucial concept in tackling domain adaptation challenges. Instead of relying on fixed domain representations, an adaptive index dynamically adjusts to reflect the inherent structure and relationships between domains. This dynamism allows for a more nuanced understanding of domain shift and enables more effective adaptation. The key benefit lies in its ability to handle complex scenarios with multiple domains and diverse variations in their characteristics. An effective approach for creating such an index might involve clustering domains based on their similarity, perhaps using a Gaussian Mixture Model, with the number of clusters dynamically determined by techniques like the Chinese Restaurant Process. This ensures the model’s flexibility to adapt to varying numbers of domains and their relationships. Another crucial aspect is the incorporation of this adaptive index within a broader domain adaptation framework, likely involving adversarial training methods to learn domain-invariant features. The integration of an adaptive domain index within such a framework promises to enhance the robustness and generalizability of domain adaptation techniques, especially when dealing with real-world scenarios where domains are rarely static and neatly categorized.
Empirical Evaluation#
An effective empirical evaluation section is crucial for validating the claims made in a research paper. It should begin by clearly defining the datasets used, their characteristics (size, distribution, etc.), and any preprocessing steps taken. Benchmark datasets are preferred for comparison with existing methods, ensuring that the results are contextually meaningful. The evaluation metrics must be appropriate to the task (e.g., accuracy, precision, recall for classification; MSE, RMSE for regression). Quantitative results should be presented clearly, including tables and/or figures to effectively visualize performance. Error bars or confidence intervals are essential to demonstrate statistical significance. Finally, the analysis should not only report raw numbers, but also provide a detailed interpretation of the results. This means discussing trends, comparing results across different settings, and identifying the aspects of the proposed method that contribute most significantly to its performance. Ablation studies are important to isolate the impact of individual components. A strong empirical evaluation section will clearly demonstrate the validity and practical significance of the proposed method, thereby strengthening the paper’s overall impact and credibility.
Future Work: GMDI#
Future work on GMDI could explore several promising avenues. Improving computational efficiency is crucial, especially for large-scale datasets. Investigating alternative methods for determining the number of Gaussian mixture components, perhaps through data-driven approaches, could significantly reduce runtime. Extending GMDI to handle more complex domain shifts warrants exploration; current methods assume a relatively simple structure between domains. Research on incorporating techniques for handling non-linear relationships or hierarchical domain structures would significantly enhance its versatility. Additionally, GMDI’s robustness to noisy or incomplete data requires thorough investigation. Developing theoretical guarantees for GMDI’s generalization performance, beyond the current evidence lower bound, would offer stronger assurances. Finally, the applicability of GMDI across different data modalities, such as time-series data or graph-structured data, should be studied. These extensions would transform GMDI into a powerful and widely applicable domain adaptation algorithm.
More visual insights#
More on figures
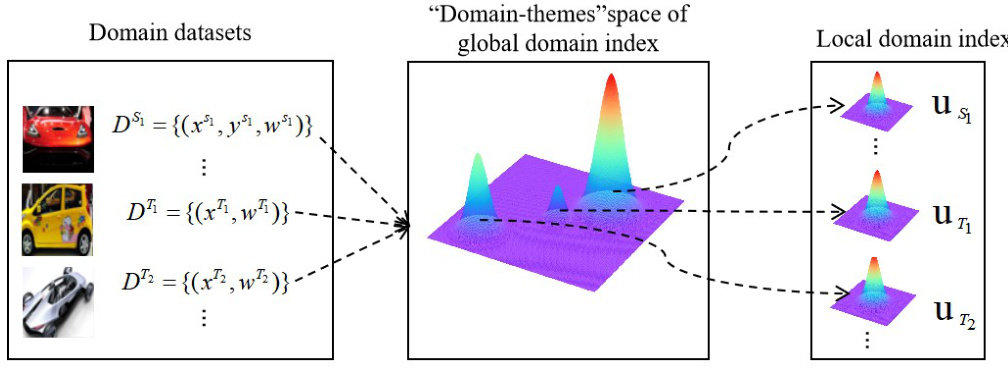
🔼 This figure illustrates the process of inferring domain indices in the proposed GMDI model. Domain datasets are processed to infer a global domain index, which is modeled as a dynamic Gaussian mixture model in the ‘domain-themes’ space. For each domain, the model selects the highest probability distribution from the mixture to derive the local domain index for each data point within that domain.
read the caption
Figure 2: The schematic diagram of domain index distributions. It shows the inference of variational Gaussian-shaped distributions for the global domain index, representing domain semantics. The process involves ranking candidate distributions in the 'domain-themes' space, selecting the highest probability one, and deriving the local domain index from it.

🔼 This figure shows the graphical models for both VDI (Variational Domain Index) and GMDI (Gaussian Mixture Domain Indexing). The left panel displays VDI, which uses a single Gaussian distribution for the global domain index θ. The right panel shows GMDI, which models the global domain index θ using a Gaussian Mixture Model (GMM), where the number of components is dynamically determined. Both models share common elements such as local domain index u, data encoding z, and the domain data Dw. The dashed line in GMDI highlights the independence assumption between the global domain index θ and data encoding z.
read the caption
Figure 3: The probabilistic graphical model of VDI (left) and GMDI (right). Edge type '-' denotes the independence between global domain index θ and data encoding z.

🔼 This figure displays the Mean Squared Error (MSE) of domain indices for two different tasks on the TPT-48 dataset. The left panel shows the MSE when adapting from 24 northern states (N) to 24 southern states (S), using latitude as the ground truth domain index. The right panel shows the MSE when adapting from 6 western states (W) to 42 eastern states (E), using longitude as the ground truth. The figure visually represents the performance of the proposed GMDI and the baseline VDI in inferring domain indices; lower MSE indicates better performance.
read the caption
Figure 4: MSE of domain indices on TPT-48 dataset. Left:N (24) → S (24), ground-truth domain indices are latitude. Right: W (6) → E (42), ground-truth domain indices are longitude.

🔼 This figure compares the data encoding generated by two different domain adaptation methods: Variational Domain Index (VDI) and the proposed Gaussian Mixture Domain-Indexing (GMDI). The t-SNE visualization shows how well each method separates data points belonging to different domains (represented by different colors). GMDI shows a much clearer separation between the domains, indicating better domain adaptation.
read the caption
Figure 7: t-SNE visualization of data encoding on CompCars dataset. Colors indicating different domains{2, 3, 4}. Left: data encoding generated by VDI. Right: data encoding generated by GMDI.

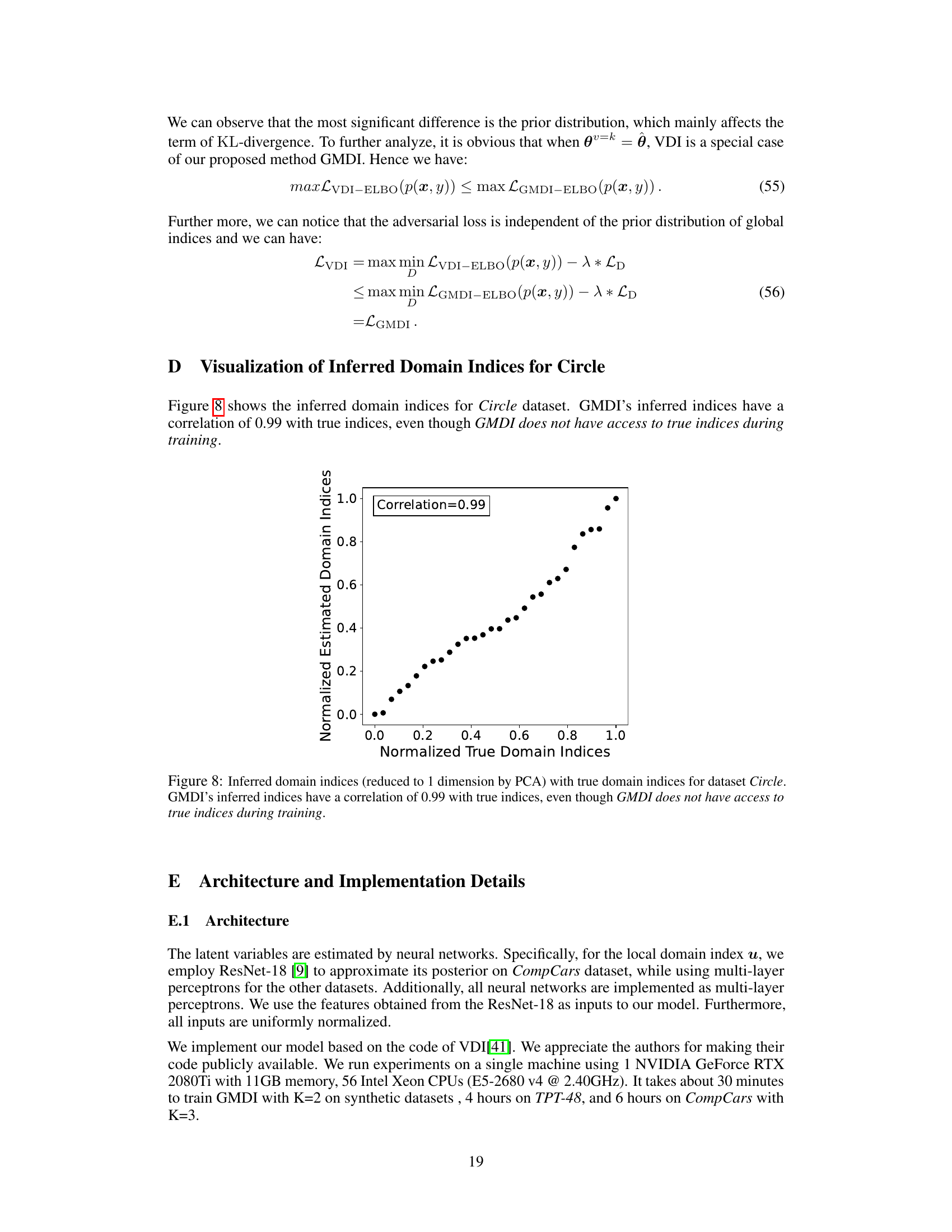
🔼 This figure shows the high correlation (0.99) between the inferred domain indices generated by the GMDI model and the true domain indices for the Circle dataset. Importantly, the GMDI model achieved this high correlation without having access to the true domain indices during training, demonstrating its effectiveness in inferring meaningful domain representations.
read the caption
Figure 8: Inferred domain indices (reduced to 1 dimension by PCA) with true domain indices for dataset Circle. GMDI's inferred indices have a correlation of 0.99 with true indices, even though GMDI does not have access to true indices during training.

🔼 The figure visualizes the Circle dataset used in the paper. The left panel shows the data points colored by their ground-truth domain indices, illustrating the distribution of different domains. The first six domains are highlighted in a green box and are designated as source domains, while the remaining domains serve as target domains. The right panel shows the ground-truth labels for the data points, with red dots representing positive labels and blue crosses representing negative labels. This visualization demonstrates the dataset’s structure and the distinction between source and target domains.
read the caption
Figure 9: The Circle dataset with 30 domains. Left: Different colors indicate ground-truth domain indices. The first 6 domains (in the green box) are source domains. Right: Ground-truth labels for Circle, with red dots and blue crosses as positive and negative data points, respectively.

🔼 This figure shows two graphs representing the geographical distribution of states in the US, divided into source and target states for two regression tasks on the TPT-48 dataset. Each graph illustrates how the target domains are categorized into three levels based on their distance from the closest source domains: level-1, level-2, and level-3. The left graph depicts the ‘W(6) -> E(42)’ task, while the right graph represents the ‘N(24) -> S(24)’ task.
read the caption
Figure 10: Domain graphs for the two adaptation tasks on TPT-48, with black nodes indicating source domains and white nodes indicating target domains. Left: Adaptation from the 24 states in the east to the 24 states in the west. Right: Adaptation from the 24 states in the north to the 24 states in the south.
More on tables
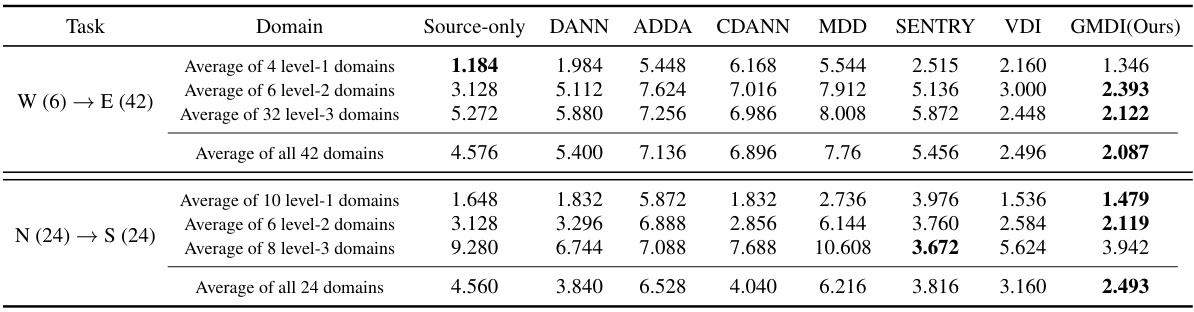
🔼 This table presents the Mean Squared Error (MSE) results for different domain adaptation methods on the TPT-48 dataset for two regression tasks: W(6)→E(42) and N(24)→S(24). The MSE is reported for the overall average across all domains, as well as broken down into averages for three levels of target domain difficulty (level-1, level-2, level-3) based on proximity to source domains. Lower MSE values indicate better performance. The best result for each subset of domains is bolded.
read the caption
Table 2: MSE for various DA methods in both tasks W (6) → E (42) and N (24) → S (24) on TPT-48. We report the average MSE of all domains as well as more detailed average MSE of level-1, level-2, level-3 target domains, respectively. Note that there is only one single DA model per column. We mark the best result with bold face.

🔼 This table presents the classification accuracy results of various domain adaptation methods on four different datasets: Circle, DG-15, DG-60, and CompCars. The datasets vary in the type of classification task (binary or 4-way) and the nature of the data. The table allows for a comparison of the proposed GMDI algorithm against several state-of-the-art domain adaptation methods, highlighting the improvement in accuracy achieved by GMDI.
read the caption
Table 1: Accuracy on binary classification tasks (Circle, DG-15, and DG-60) and 4-way classification task (CompCars).

🔼 This table presents the classification accuracy results achieved by different domain adaptation methods on four benchmark datasets: Circle (binary classification), DG-15 (binary classification), DG-60 (binary classification), and CompCars (4-way classification). The performance of each method is compared to a baseline where the model is trained only on source data (‘Source-only’). The table highlights the improvement in accuracy achieved by GMDI compared to other state-of-the-art methods.
read the caption
Table 1: Accuracy on binary classification tasks (Circle, DG-15, and DG-60) and 4-way classification task (CompCars).

🔼 This table presents the Mean Squared Error (MSE) achieved by different domain adaptation methods on the TPT-48 dataset for two regression tasks: W (6) → E (42) and N (24) → S (24). The MSE is reported for all domains, as well as broken down by level of difficulty (level-1, level-2, and level-3 target domains, representing increasing distance from the source domain). The best result for each setting is highlighted in bold.
read the caption
Table 2: MSE for various DA methods in both tasks W (6) → E (42) and N (24) → S (24) on TPT-48. We report the average MSE of all domains as well as more detailed average MSE of level-1, level-2, level-3 target domains, respectively. Note that there is only one single DA model per column. We mark the best result with bold face.

🔼 This table presents the accuracy, total training time, number of epochs, and time per epoch for three different methods on the CompCars dataset. The methods are VDI, GMDI without CRP (Chinese Restaurant Process), and GMDI with CRP. The table shows that GMDI achieves the highest accuracy (44.4%) but takes slightly more time per epoch (26s) compared to VDI (19s) and GMDI without CRP (21s). The total training time is comparable across the three methods, indicating that the added computational cost of the CRP in GMDI is offset by faster convergence.
read the caption
Table 6: The results of the ablation and computational cost experiments on CompCars.
Full paper#