TL;DR#
Reinforcement learning often struggles in scenarios with partial observability, where agents only have incomplete information about the environment. Existing methods that use complete state information during training often encounter unstable learning due to high variance. This is because they over-rely on the complete state, causing instability when dealing with real-world uncertainties.
To address this, the authors propose DCRL (Dual Critic Reinforcement Learning), a novel framework that uses two critics: one with full state information (oracle) and another with only partial observations. A synergistic strategy smoothly transitions and weighs these critics, leveraging the strengths of each while reducing variance and maintaining unbiasedness. The theoretical analysis proves its unbiasedness and variance reduction, and empirical results demonstrate that DCRL outperforms existing methods across various challenging environments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on reinforcement learning under partial observability, a pervasive challenge in real-world applications. It offers a novel solution to improve sample efficiency and stabilize learning by leveraging readily available full-state information during training, without sacrificing unbiasedness. This opens new avenues for research in variance reduction techniques and adaptive learning strategies, significantly impacting the development of robust and efficient RL agents for complex, real-world problems.
Visual Insights#
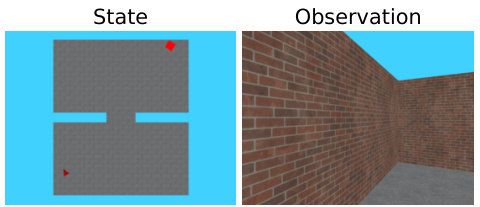
🔼 This figure shows a comparison between the full state and the partial observation available to the agent in the WallGap environment of MiniWorld. The left image displays the complete state, revealing the agent’s location (red triangle), the target location (red box), and the overall map layout. The right image represents the partial observation the agent receives, showcasing a limited first-person perspective that obscures much of the environment. This illustrates the challenge of decision-making under partial observability in reinforcement learning.
read the caption
Figure 1: The WallGap environment, a procedurally generated navigation task in MiniWorld. The agent's goal (red triangle) is to reach the target (red box) within as few steps as possible under partial observability.
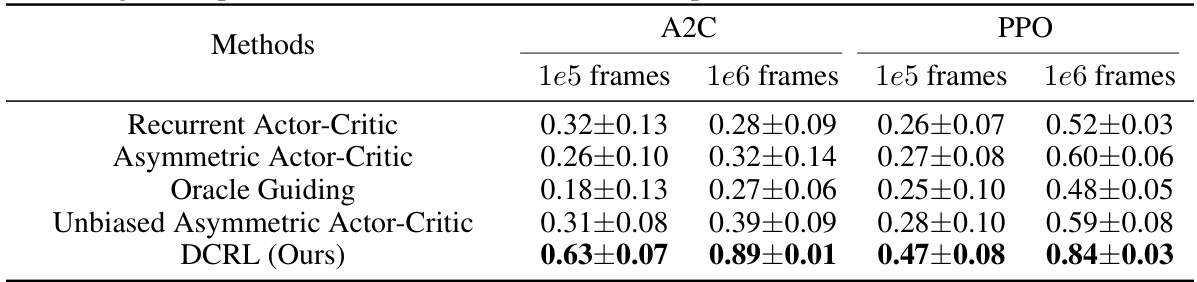
🔼 This table presents the performance comparison of different RL algorithms on MiniGrid environment in terms of average return after 1e5 and 1e6 frames of training. The algorithms compared are Recurrent Actor-Critic, Asymmetric Actor-Critic, Oracle Guiding, Unbiased Asymmetric Actor-Critic, and DCRL (the proposed method). The mean and standard error of the performance are reported for each algorithm and training duration. This shows the relative performance of each algorithm across different training durations.
read the caption
Table 1: Performance of agents on MiniGrid after 1e5 frames (27 games) and 1e6 frames (13 games) of training. We report the mean and standard error of the performance.
In-depth insights#
DCRL Framework#
The DCRL framework, a Dual Critic Reinforcement Learning approach, innovatively addresses the challenges of partial observability in reinforcement learning. It elegantly combines the strengths of two distinct critics: a standard critic operating solely on observable history and an oracle critic leveraging the complete state information available during training. This asymmetric design enables efficient learning by harnessing full-state knowledge while mitigating the variance often associated with over-reliance on complete states. A synergistic weighting mechanism seamlessly transitions between the two critics, dynamically adjusting their influence based on the observed learning progress and uncertainty. This intelligent blending reduces variance while maintaining unbiasedness, leading to improved online performance. Theoretical analysis and extensive empirical evaluations demonstrate the superiority of DCRL in several benchmark environments. The framework’s simplicity, adaptability, and theoretical grounding makes it a significant contribution to the field of partial observability RL.
Dual Critic Synergy#
The concept of “Dual Critic Synergy” in reinforcement learning proposes a powerful approach to address the challenges of partial observability. By employing two distinct critics, one with access to the complete state (the oracle critic) and another operating solely on observable information (the standard critic), this framework aims to leverage the strengths of both. The oracle critic enhances learning efficiency by providing a more accurate value function estimate, while the standard critic mitigates variance and promotes robustness in online performance. A key innovation lies in the synergistic strategy that seamlessly transitions and weights the outputs of both critics, optimizing the balance between efficiency and stability. This approach is theoretically grounded, with proofs demonstrating unbiasedness and variance reduction. The method’s effectiveness is experimentally validated, showcasing superior performance across various environments compared to alternative approaches. Adaptive weighting mechanisms, responsive to the performance of both critics, dynamically balance the contributions of complete and partial state information. This dynamic adaptation proves crucial in navigating uncertain environments, effectively leveraging full-state information during training while ensuring reliable performance during deployment where access to full states is limited.
Variance Reduction#
The concept of variance reduction is central to the success of reinforcement learning, especially in complex environments. High variance in learning can lead to unstable training and poor generalization. The paper tackles this challenge by introducing a dual-critic reinforcement learning framework (DCRL). DCRL cleverly utilizes both a standard critic operating on limited observations and an oracle critic with access to the full state, achieving a balance. The oracle critic enhances learning efficiency, while the standard critic mitigates the variance introduced by the oracle. A key innovation is a weighting mechanism that dynamically blends the advantages of both critics. This adaptive strategy not only improves performance but also contributes to theoretical unbiasedness. The theoretical analysis and empirical results convincingly showcase DCRL’s superior performance over traditional methods in challenging partially observable scenarios. The weighting mechanism acts as a form of robust regularization, preventing overreliance on potentially noisy complete-state information. In essence, DCRL presents a well-founded and effective solution to the persistent problem of variance in reinforcement learning, particularly relevant to real-world applications with partial observability.
MiniGrid & MiniWorld#
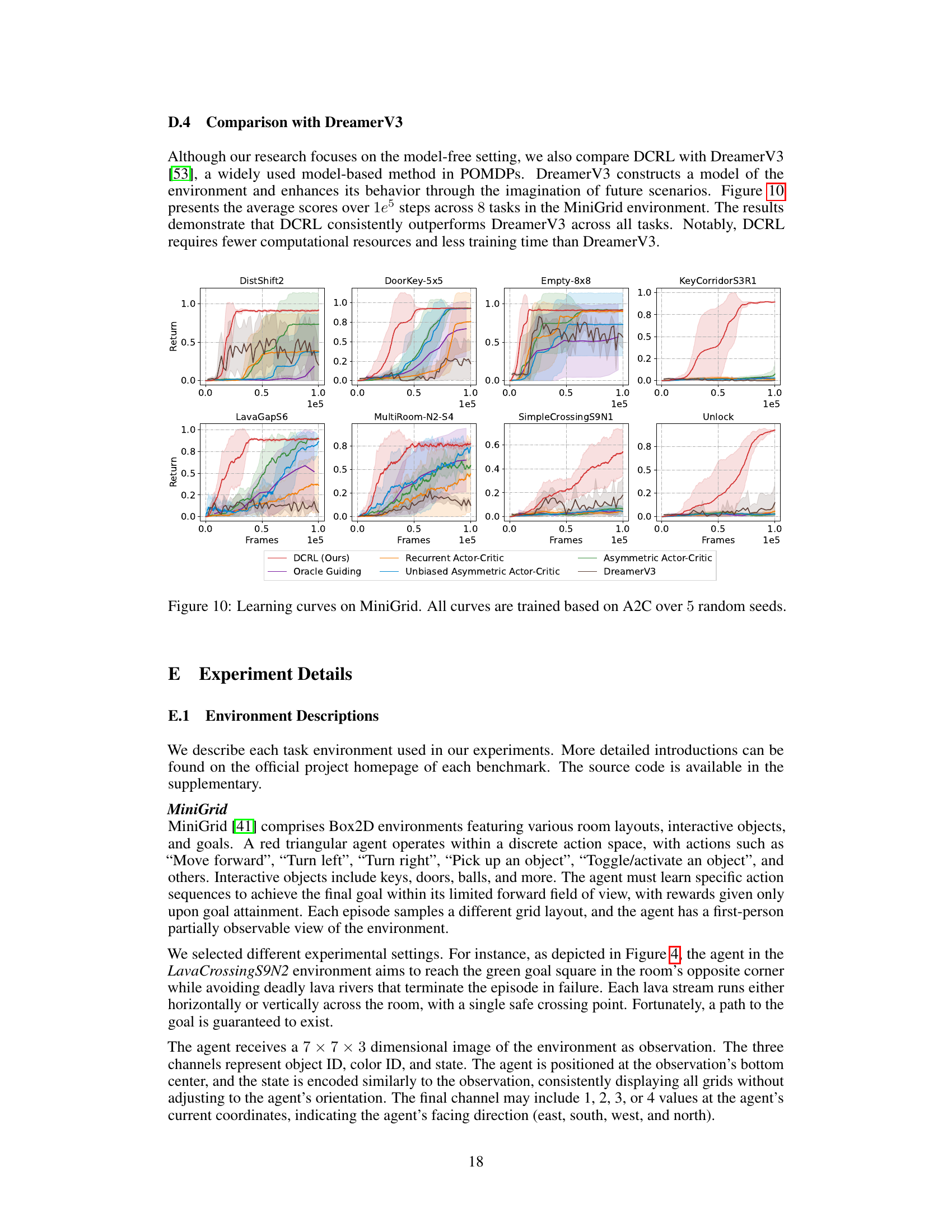
The experimental evaluation of the proposed Dual Critic Reinforcement Learning (DCRL) framework is conducted on MiniGrid and MiniWorld environments. MiniGrid, a procedurally generated environment, presents various goal-oriented tasks with partial observability. DCRL’s performance is compared against baselines like Recurrent Actor-Critic, Asymmetric Actor-Critic, and Unbiased Asymmetric Actor-Critic across multiple MiniGrid tasks. The results demonstrate that DCRL outperforms these baselines in most scenarios, showcasing its effectiveness in partially observable environments. MiniWorld, on the other hand, offers more complex continuous state space tasks, further testing DCRL’s robustness. Again, DCRL is shown to improve upon baseline methods, particularly those that do not effectively utilize state information. The consistent superior performance of DCRL in both MiniGrid and MiniWorld highlights its ability to mitigate the high variance often associated with using full state information during training while retaining unbiasedness. These results strongly support the core claims of the paper.
Future Works#
Future work could explore several promising directions. Extending DCRL to handle more complex environments with continuous state and action spaces is crucial, requiring investigation of appropriate function approximation techniques. Addressing the computational cost of DCRL, particularly with large state spaces, might involve exploring more efficient architectures or approximation methods. Investigating alternative weighting strategies between the oracle and standard critics, possibly incorporating adaptive or learned weighting schemes, could improve performance. Theoretical analysis of DCRL’s convergence properties under various assumptions warrants further study. Finally, empirical evaluations on diverse real-world problems should be conducted to demonstrate DCRL’s generalizability and practical applicability.
More visual insights#
More on figures
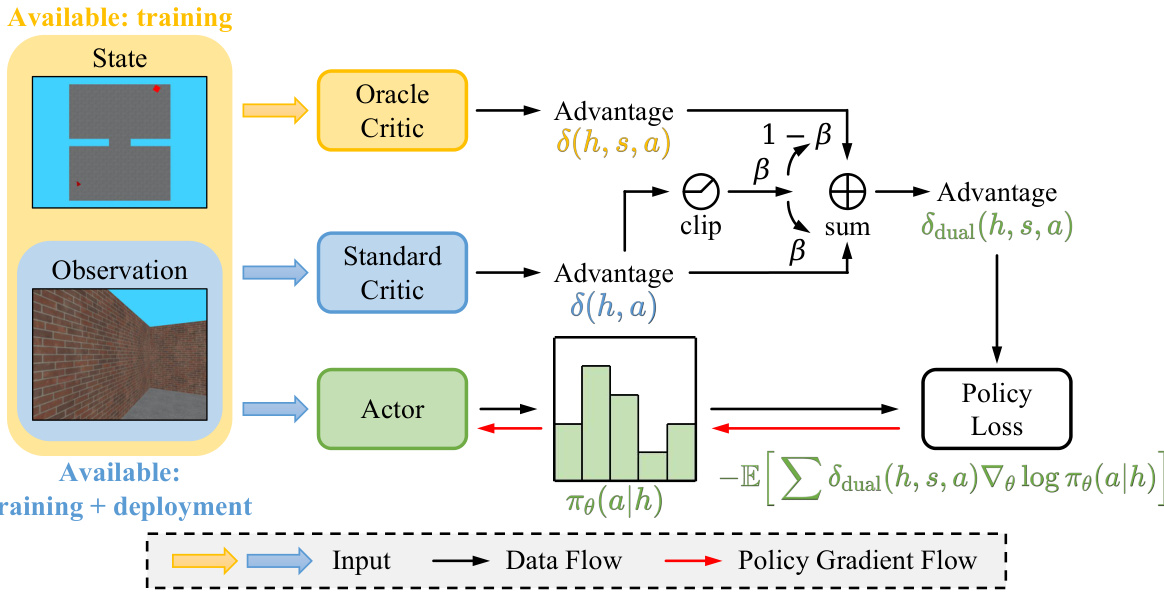
🔼 This figure illustrates the architecture of the Dual Critic Reinforcement Learning (DCRL) framework. It shows how the two critics (oracle and standard) process the state and observation information separately. The oracle critic uses both history and full state information, while the standard critic only uses history. A weighting mechanism (β) combines the advantages from both critics to mitigate variance while improving efficiency. This combined advantage is then used to update the actor’s policy, minimizing the policy loss. The figure also highlights the data flow and policy gradient flow through the system.
read the caption
Figure 2: Implementation of DCRL framework. DCRL innovates a synergistic strategy to meld the strengths of the oracle critic for efficiency improvement and the standard critic for variance reduction.

🔼 This figure shows the learning curves of different reinforcement learning algorithms on MiniGrid, a partially observable environment. The algorithms compared include DCRL, Recurrent Actor-Critic, Asymmetric Actor-Critic, Oracle Guiding, and Unbiased Asymmetric Actor-Critic. The x-axis represents the number of training frames, and the y-axis represents the average return achieved by the agents. The shaded bars represent the standard error across 5 different random seeds. The figure demonstrates the superior performance of DCRL compared to other baseline algorithms.
read the caption
Figure 3: Learning curves on MiniGrid. The x-axis and y-axis represent the training frames and average returns, respectively. Shaded bars illustrate the standard error. All curves are trained based on A2C over 5 random seeds.
🔼 This figure shows a comparison between the full state and the partial observation available to the agent in the WallGap environment of MiniWorld. The full state reveals the complete layout of the environment, including the agent’s location (red triangle), the goal location (red box), and obstacles (orange wavy blocks). However, the agent only perceives a partial observation, which is a limited field of view and doesn’t show the complete environment layout. This illustrates the challenge of partial observability in reinforcement learning, where the agent must make decisions based on incomplete information.
read the caption
Figure 1: The WallGap environment, a procedurally generated navigation task in MiniWorld. The agent's goal (red triangle) is to reach the target (red box) within as few steps as possible under partial observability.
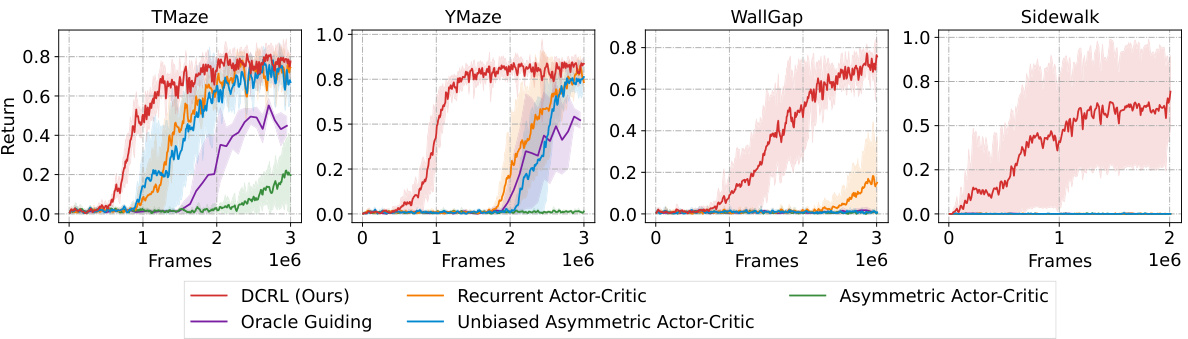
🔼 This figure shows the learning curves of different reinforcement learning algorithms on four different MiniWorld environments. The algorithms compared are DCRL (the authors’ proposed method), Recurrent Actor-Critic, Asymmetric Actor-Critic, Oracle Guiding, and Unbiased Asymmetric Actor-Critic. The x-axis represents the number of training frames, and the y-axis represents the average return achieved by each algorithm. The shaded area around each line represents the standard error. All experiments were run 5 times with different random seeds using the Proximal Policy Optimization (PPO) algorithm.
read the caption
Figure 5: Learning curves on MiniWorld. The x-axis and y-axis represent the training frames and average returns, respectively. All curves are trained based on PPO over 5 random seeds.
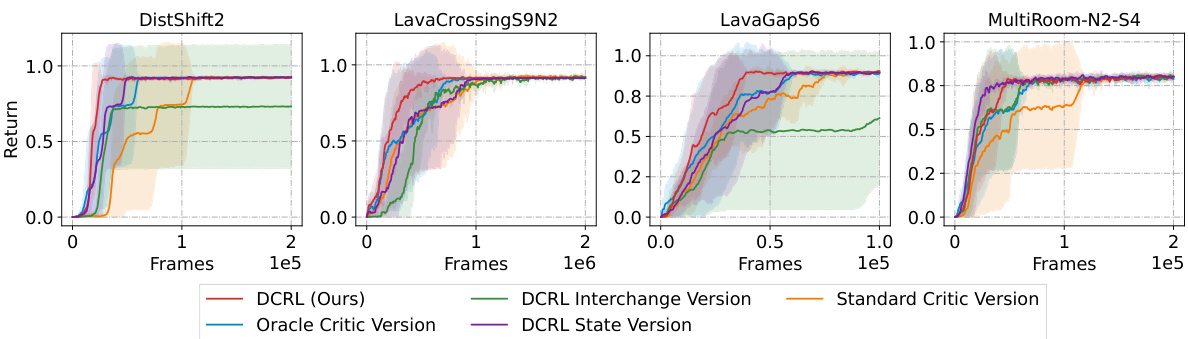
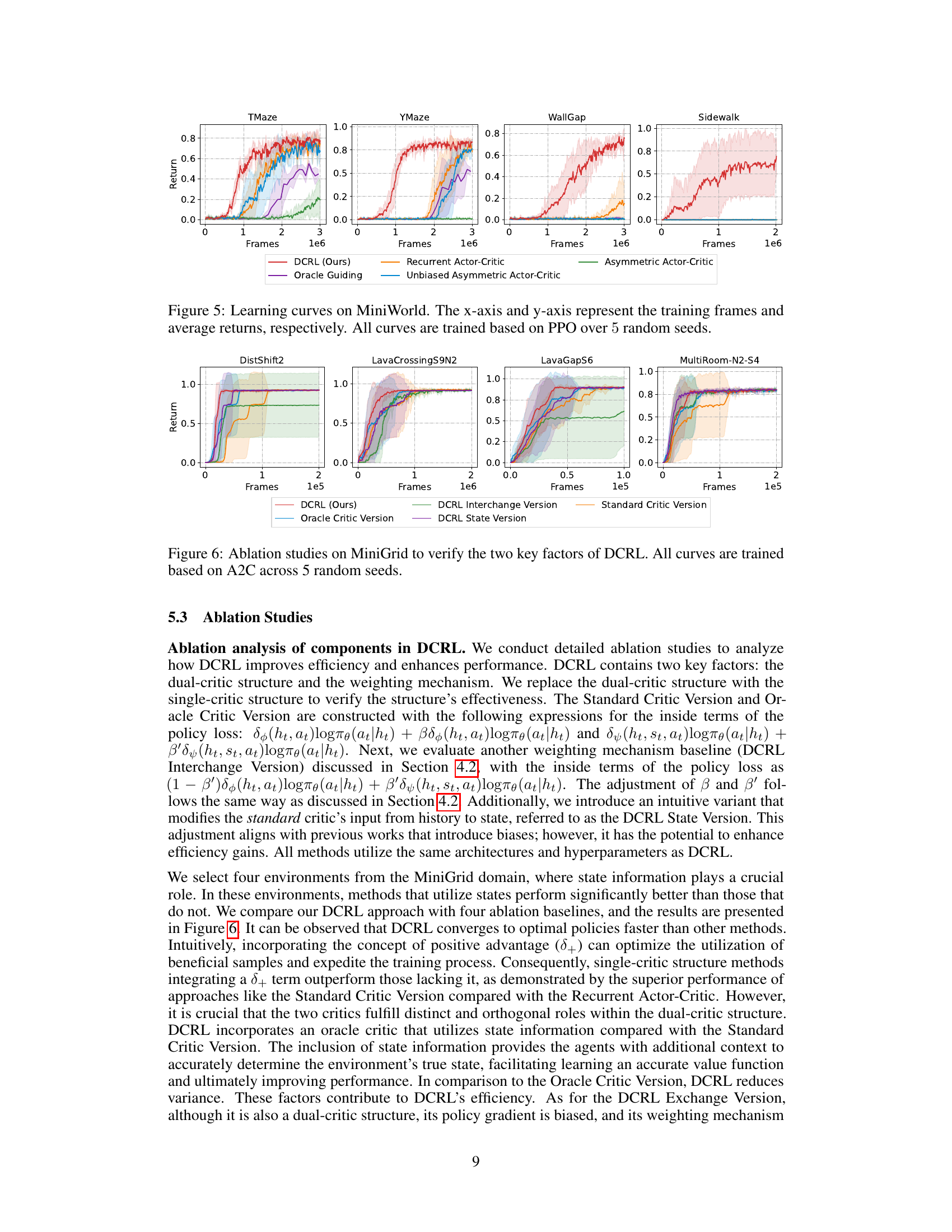
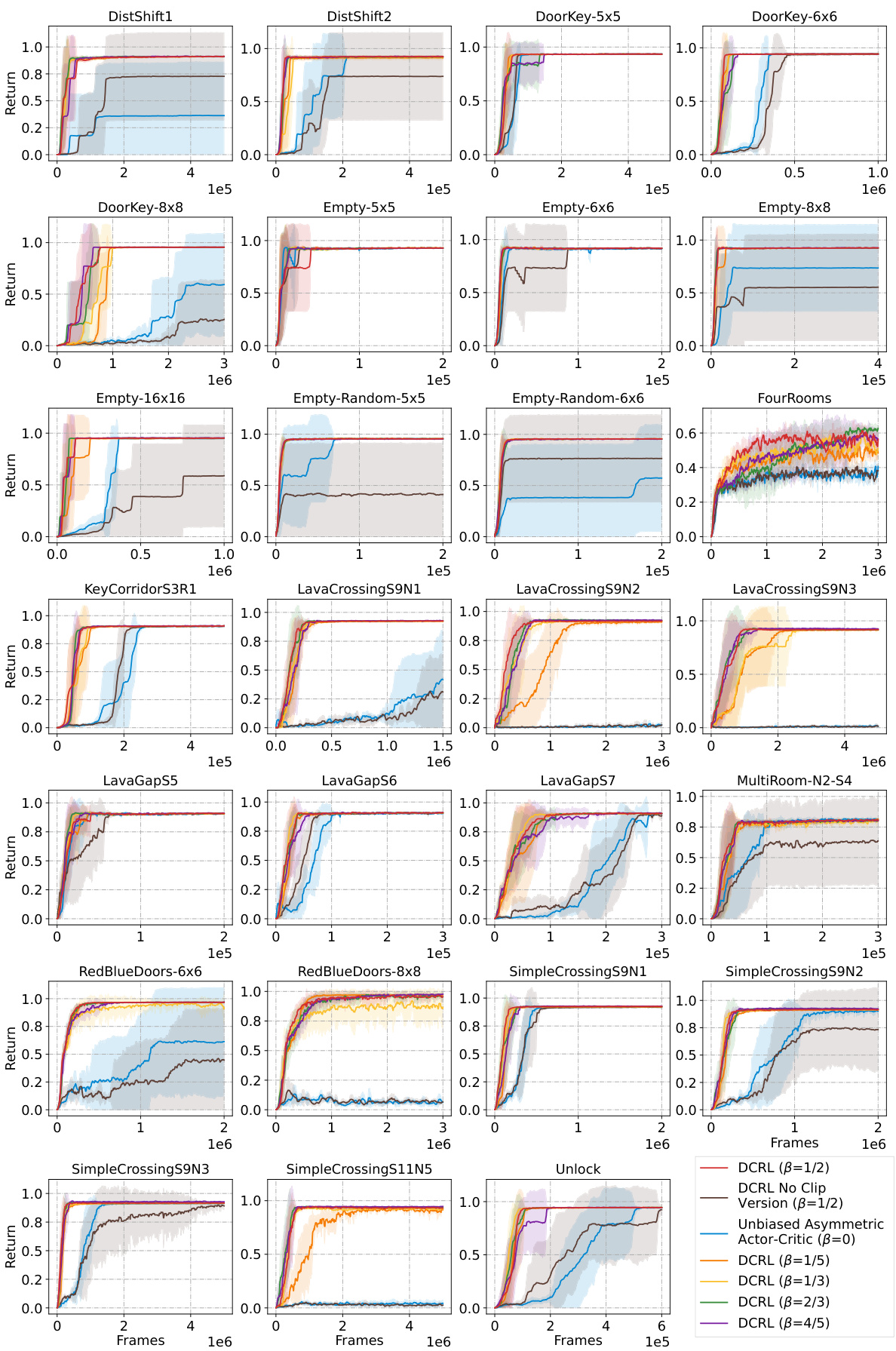
🔼 This figure presents ablation studies conducted on the MiniGrid environment to analyze the impact of the dual-critic structure and the weighting mechanism in the DCRL framework. Four different versions of the DCRL model are compared against the Unbiased Asymmetric Actor-Critic baseline. The versions include a version using only the standard critic, a version using only the oracle critic, and a version using an altered weighting mechanism that balances the contributions of the two critics differently. All results are based on the A2C algorithm, trained five times for each condition.
read the caption
Figure 6: Ablation studies on MiniGrid to verify the two key factors of DCRL. All curves are trained based on A2C across 5 random seeds.

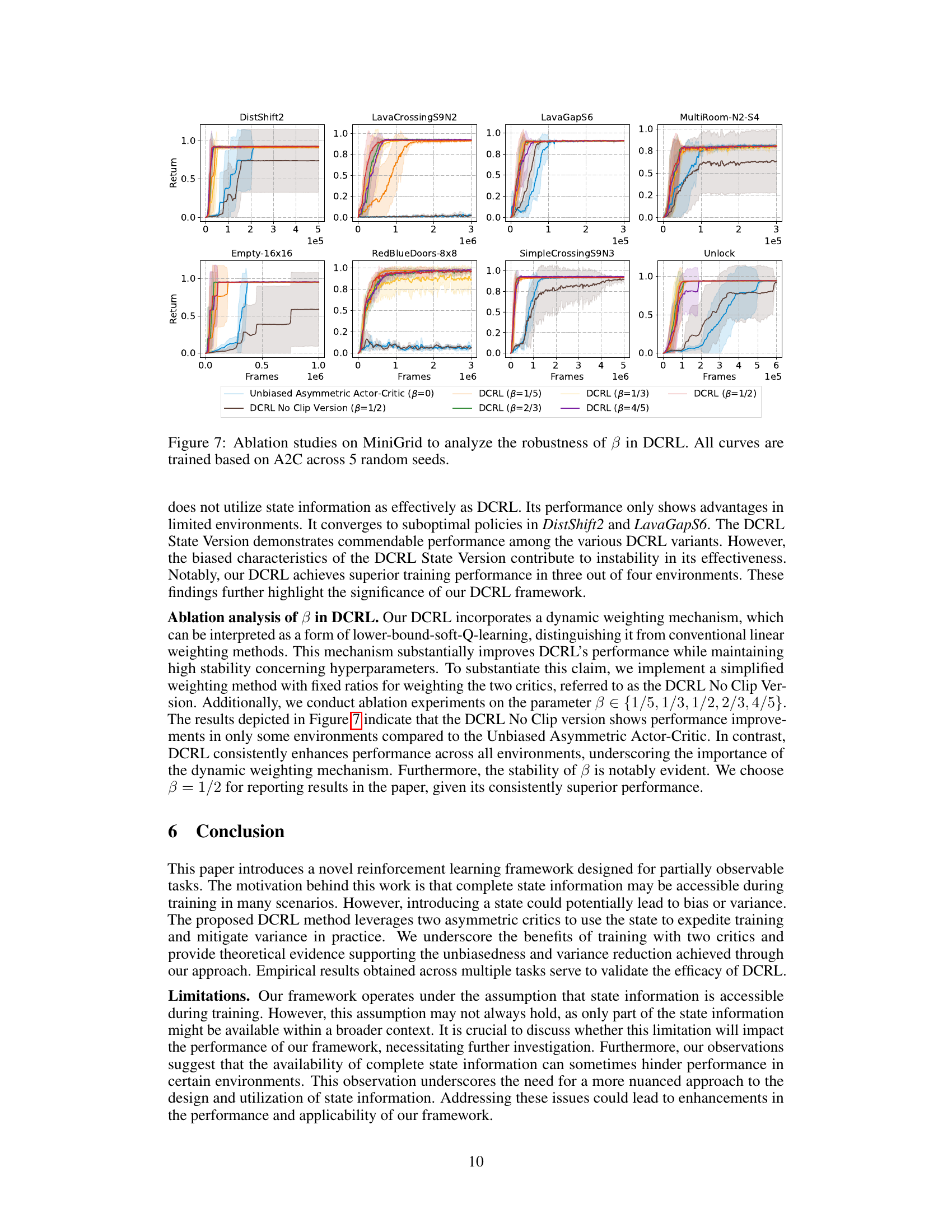
🔼 This figure displays ablation studies performed on the MiniGrid environment to evaluate the impact of the weighting parameter β within the DCRL framework. Different values of β are tested (1/5, 1/3, 1/2, 2/3, 4/5), and a ’no clip’ version of DCRL is included for comparison. A control using the unbiased asymmetric actor-critic (β=0) is also shown. The x-axis represents training frames, and the y-axis represents average returns. The shaded areas indicate standard error across 5 random seeds. The results demonstrate the robustness of DCRL to different β values while highlighting the effectiveness of its dynamic weighting mechanism.
read the caption
Figure 7: Ablation studies on MiniGrid to analyze the robustness of β in DCRL. All curves are trained based on A2C across 5 random seeds.
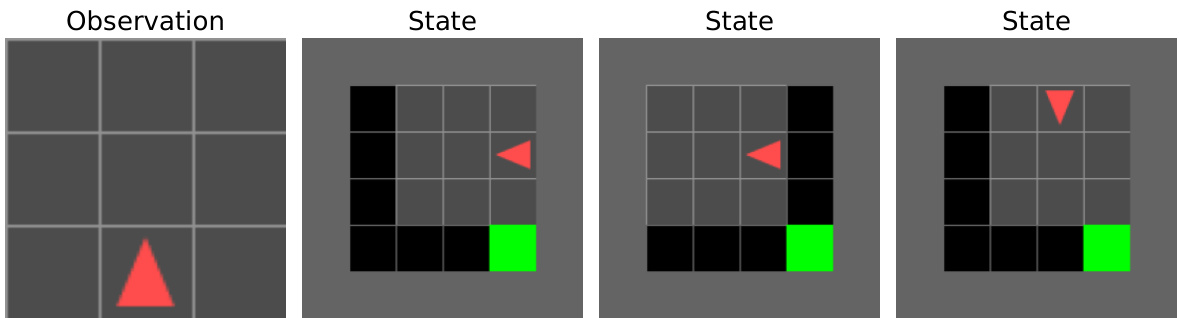
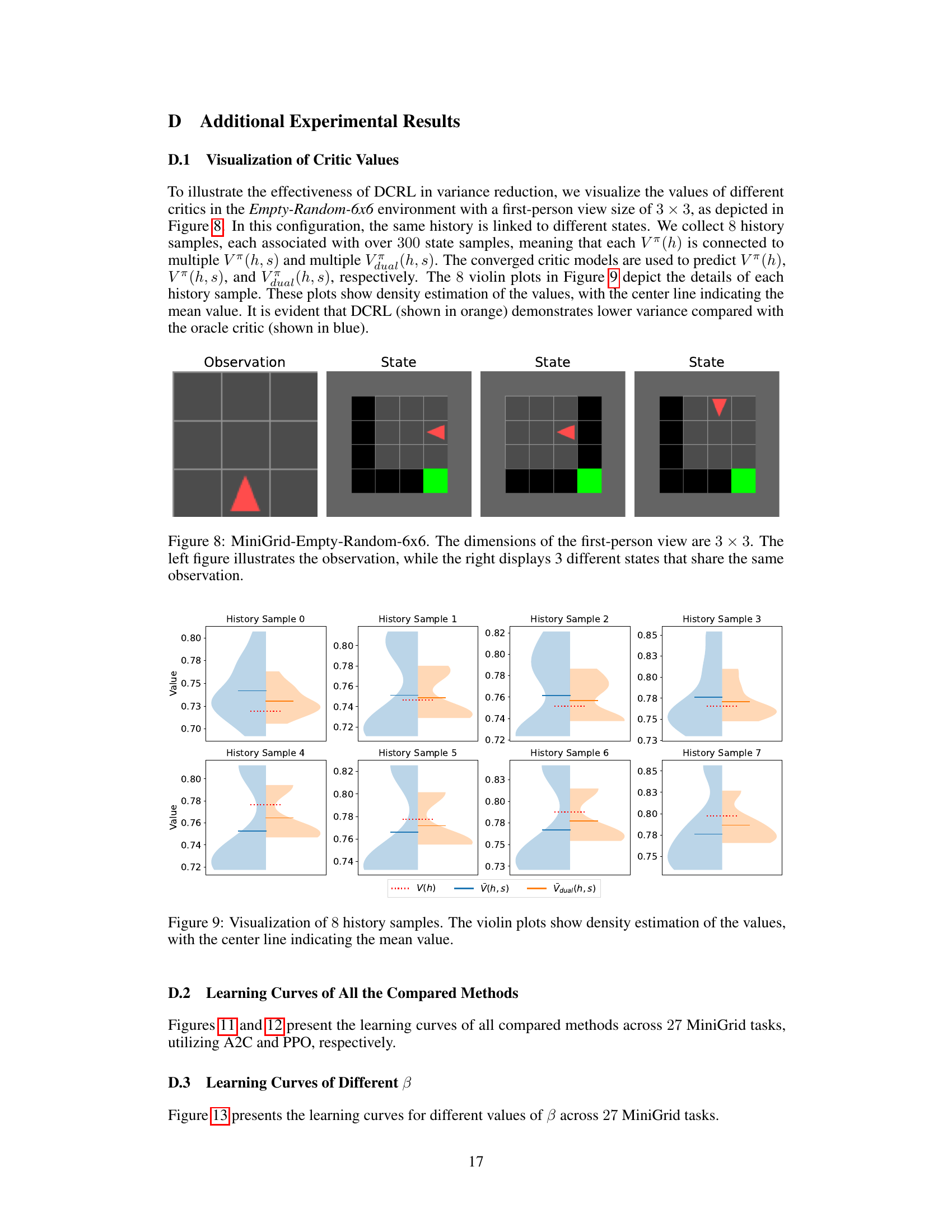
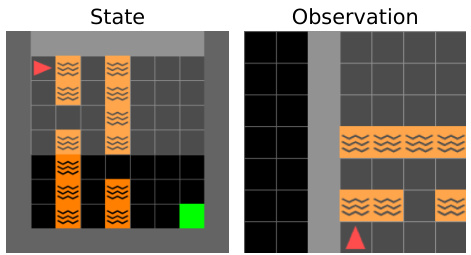
🔼 This figure shows an example from the MiniGrid-Empty-Random-6x6 environment. The leftmost panel displays the limited observation available to the agent (a 3x3 grid). The remaining panels illustrate three different complete states, which are not directly observable to the agent but are available during training, that all share the same observation shown in the leftmost panel. This highlights the concept of partial observability in the environment.
read the caption
Figure 8: MiniGrid-Empty-Random-6x6. The dimensions of the first-person view are 3 × 3. The left figure illustrates the observation, while the right displays 3 different states that share the same observation.

🔼 This figure visualizes the density estimation of values for three different critic models (V(h), V(h,s), Vdual(h,s)) across 8 different history samples in the Empty-Random-6x6 environment of MiniGrid. Each violin plot shows the distribution of values for a specific history sample, providing a visual comparison of the variance and bias of the different critic models. The center line within each violin plot indicates the mean value for that particular history sample.
read the caption
Figure 9: Visualization of 8 history samples. The violin plots show density estimation of the values, with the center line indicating the mean value.
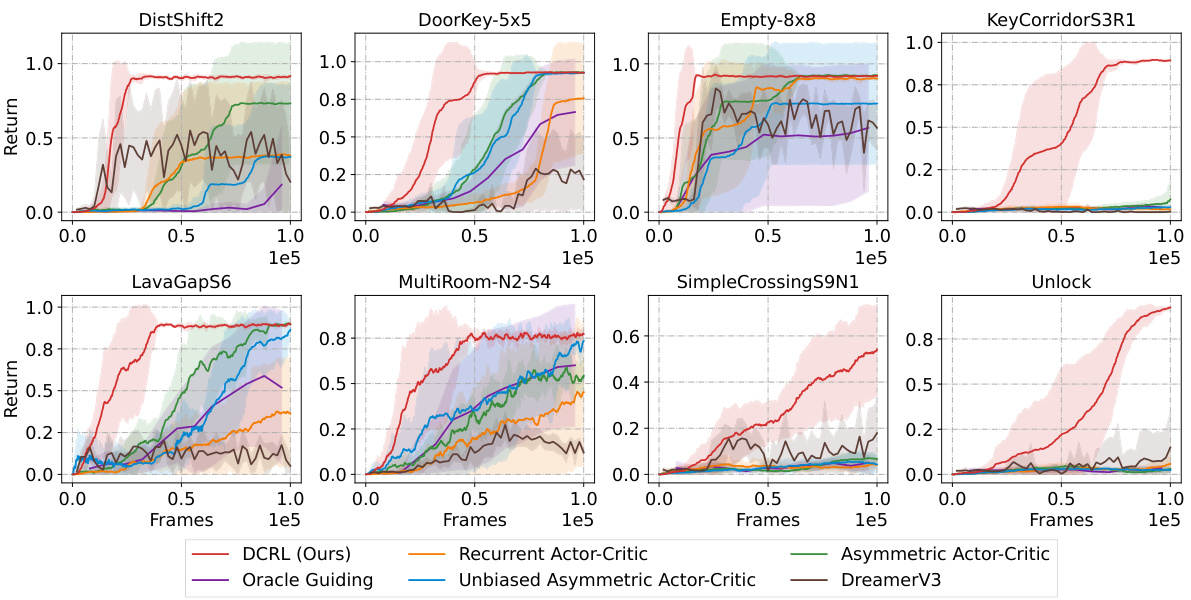
🔼 This figure compares the performance of DCRL against several baselines on 8 different MiniGrid tasks. The x-axis represents training frames, and the y-axis represents average returns. Shaded areas indicate standard errors. The figure shows DCRL consistently outperforming other methods across the tasks, highlighting its effectiveness in partially observable environments.
read the caption
Figure 10: Learning curves on MiniGrid. All curves are trained based on A2C over 5 random seeds.
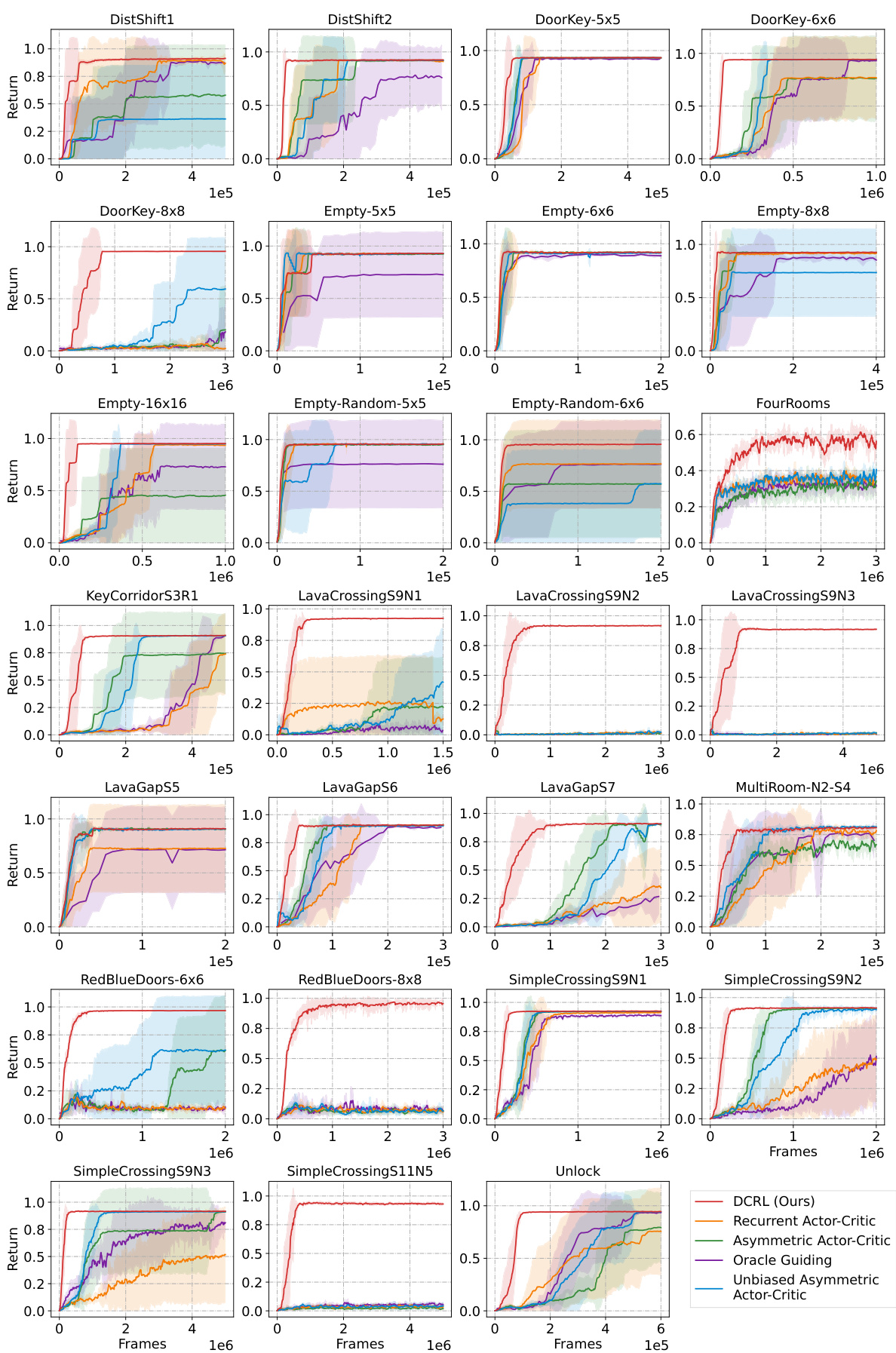
🔼 This figure shows the learning curves of different reinforcement learning algorithms on MiniGrid environments. The x-axis represents the number of training frames, and the y-axis represents the average return achieved by each algorithm. The shaded bars show the standard error across 5 random seeds for each algorithm. The algorithms compared include DCRL (the proposed method), Recurrent Actor-Critic, Asymmetric Actor-Critic, Oracle Guiding, and Unbiased Asymmetric Actor-Critic. The figure demonstrates the performance of DCRL compared to existing methods across several MiniGrid tasks.
read the caption
Figure 3: Learning curves on MiniGrid. The x-axis and y-axis represent the training frames and average returns, respectively. Shaded bars illustrate the standard error. All curves are trained based on A2C over 5 random seeds.
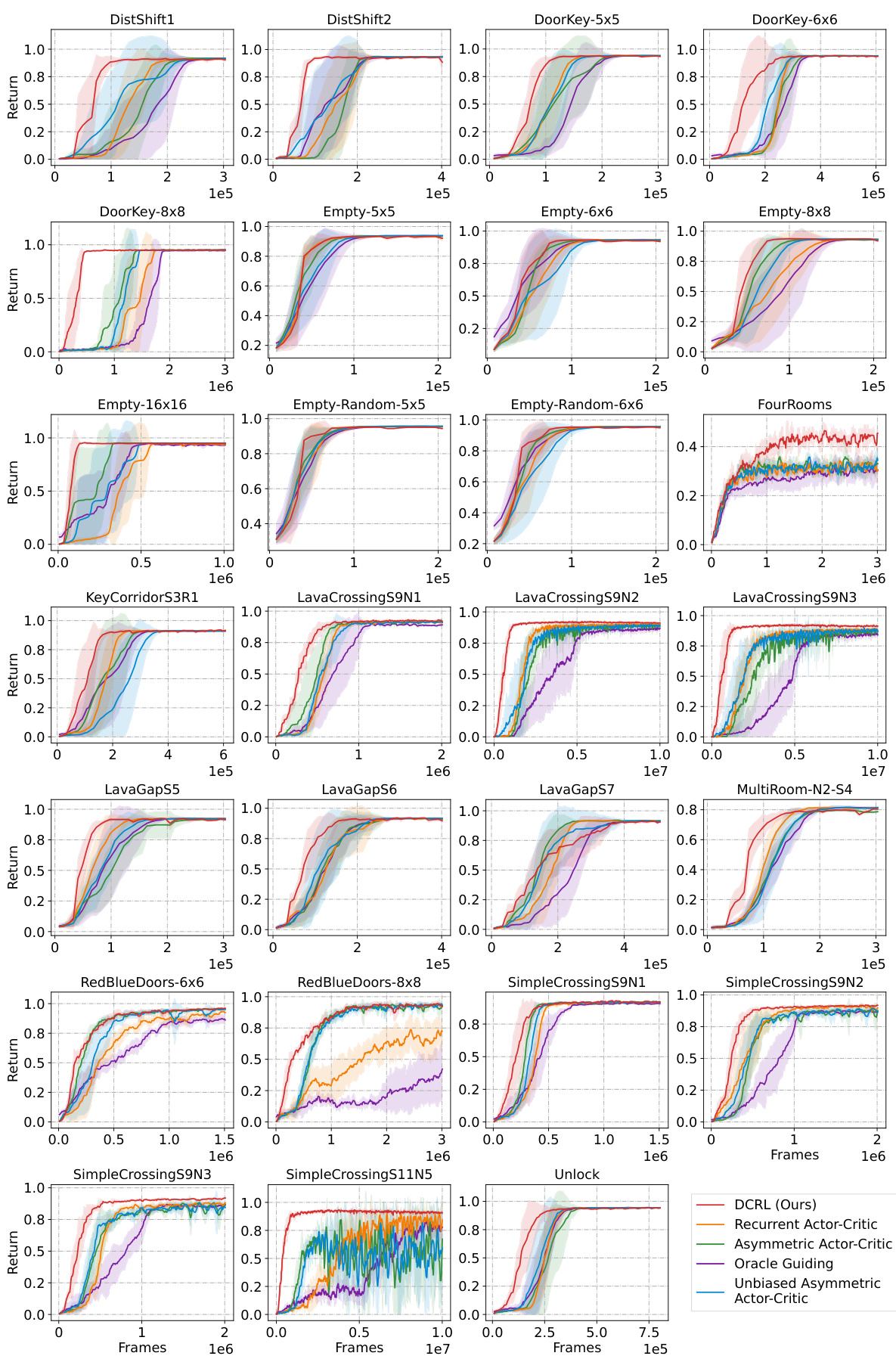
🔼 This figure shows the learning curves of different reinforcement learning algorithms on various MiniGrid environments. The x-axis represents the number of training frames, and the y-axis represents the average return (reward) achieved by the agent. Each curve represents a different algorithm: DCRL (the authors’ proposed method), Recurrent Actor-Critic, Asymmetric Actor-Critic, Oracle Guiding, and Unbiased Asymmetric Actor-Critic. The shaded regions represent the standard error, indicating the variability in performance across different random seeds. The figure demonstrates the relative performance of DCRL compared to existing methods on these tasks.
read the caption
Figure 3: Learning curves on MiniGrid. The x-axis and y-axis represent the training frames and average returns, respectively. Shaded bars illustrate the standard error. All curves are trained based on A2C over 5 random seeds.
🔼 This figure shows the learning curves of different reinforcement learning algorithms on 27 MiniGrid tasks. The x-axis represents the number of training frames, and the y-axis represents the average return. The algorithms compared are DCRL (the proposed method with different beta values), Recurrent Actor-Critic, Asymmetric Actor-Critic, Oracle Guiding, and Unbiased Asymmetric Actor-Critic. The shaded regions represent the standard error. The results demonstrate DCRL’s superior performance across most tasks.
read the caption
Figure 11: Learning curves on MiniGrid. All curves are trained based on A2C over 5 random seeds.
Full paper#