↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
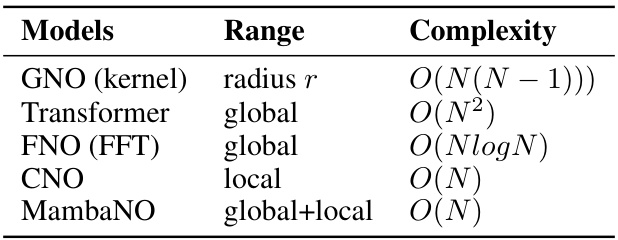
Traditional methods for solving Partial Differential Equations (PDEs) often involve expensive computational costs and struggle to capture both global and local features of the functions involved. Neural operators (NOs) offer a data-driven alternative, but many existing NOs suffer from high computational complexity or limitations in capturing holistic function information. Previous methods, like GNO, FNO, and Transformer-based NOs, exhibit complexities of O(N(N-1)), O(NlogN), and O(N^2), respectively, hindering their scalability.
This paper introduces MambaNO, a novel neural operator designed to overcome these limitations. MambaNO cleverly balances global and local integration using a state space model (Mamba) for global scanning and an alias-free architecture for local integration. The authors demonstrate the continuous-discrete equivalence property of MambaNO and show that it achieves state-of-the-art results on various benchmark PDEs, surpassing existing methods in both efficiency and accuracy with fewer parameters.
Key Takeaways#
Why does it matter?#
This paper is important because it presents MambaNO, a novel and efficient neural operator for solving partial differential equations. Its linear time complexity and state-of-the-art performance on various benchmarks make it a significant contribution to the field, opening new avenues for research in scientific machine learning and numerical methods. The alias-free framework ensures robustness and accuracy, addressing limitations of existing methods. This is particularly relevant given the growing interest in using machine learning for solving complex scientific problems.
Visual Insights#

This figure shows the overall architecture of the Mamba Neural Operator (MambaNO). It is a U-Net-like architecture with multiple stages of downsampling and upsampling. Each stage involves two convolution integrations and two Mamba integrations. The Mamba integration is a novel integral form proposed in this paper, which aims to balance global and local information processing for efficient PDE solving. The state space model (SSM) is also integrated into the architecture to capture global information effectively. Activation functions (Act) are applied after each integration and normalization step. The architecture combines convolution and Mamba integrations to approximate a well-behaved mapping from input function spaces (boundary conditions) to output function spaces (solutions of PDEs). The different blocks in the diagram represent the various operations performed during inference.

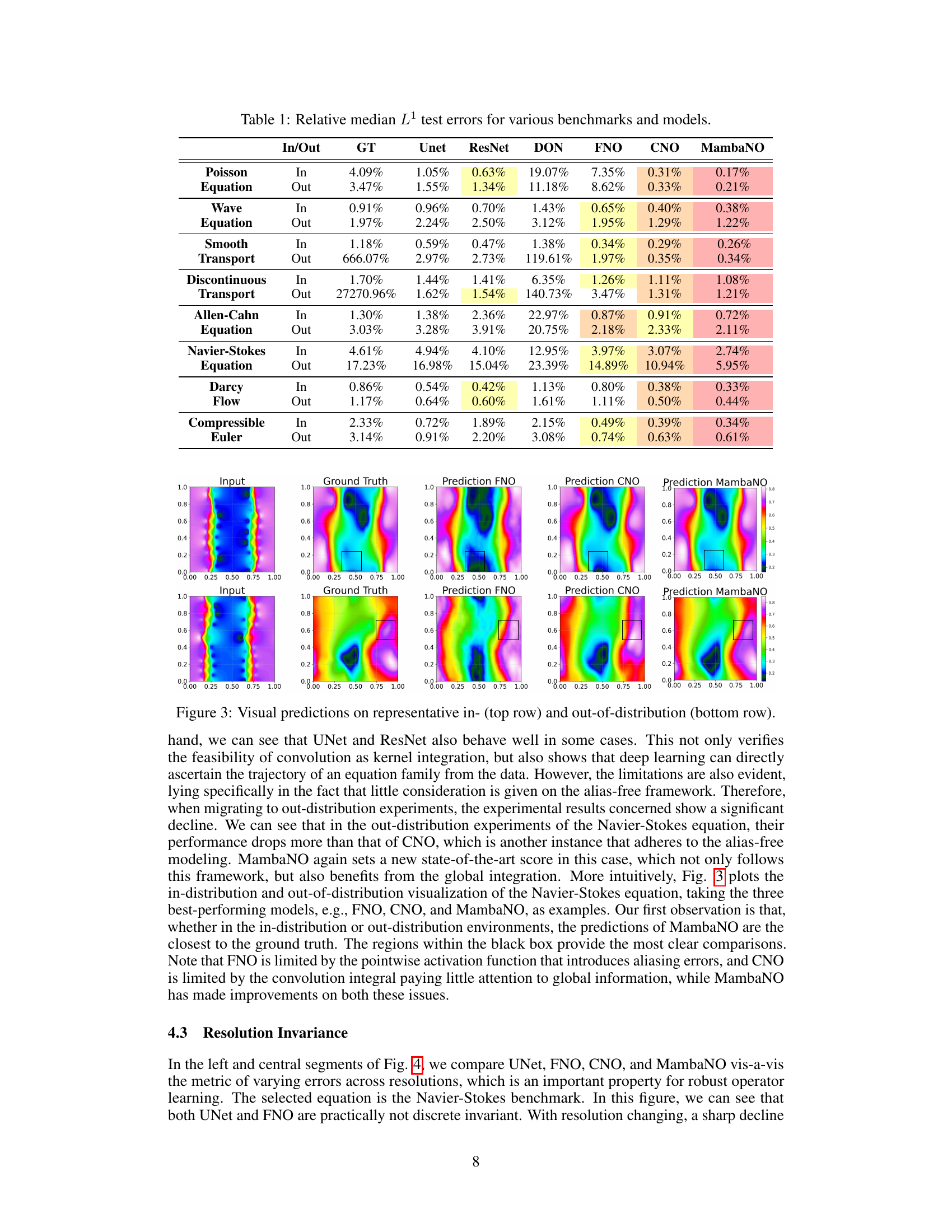
This table presents the relative median L¹ test errors achieved by different models (GT, Unet, ResNet, DON, FNO, CNO, and MambaNO) on various benchmark PDEs. The results are categorized as ‘In’ (in-distribution) and ‘Out’ (out-of-distribution) to indicate whether the test data was drawn from the same distribution as the training data. Lower values indicate better performance.
In-depth insights#
Alias-Free MambaNO#
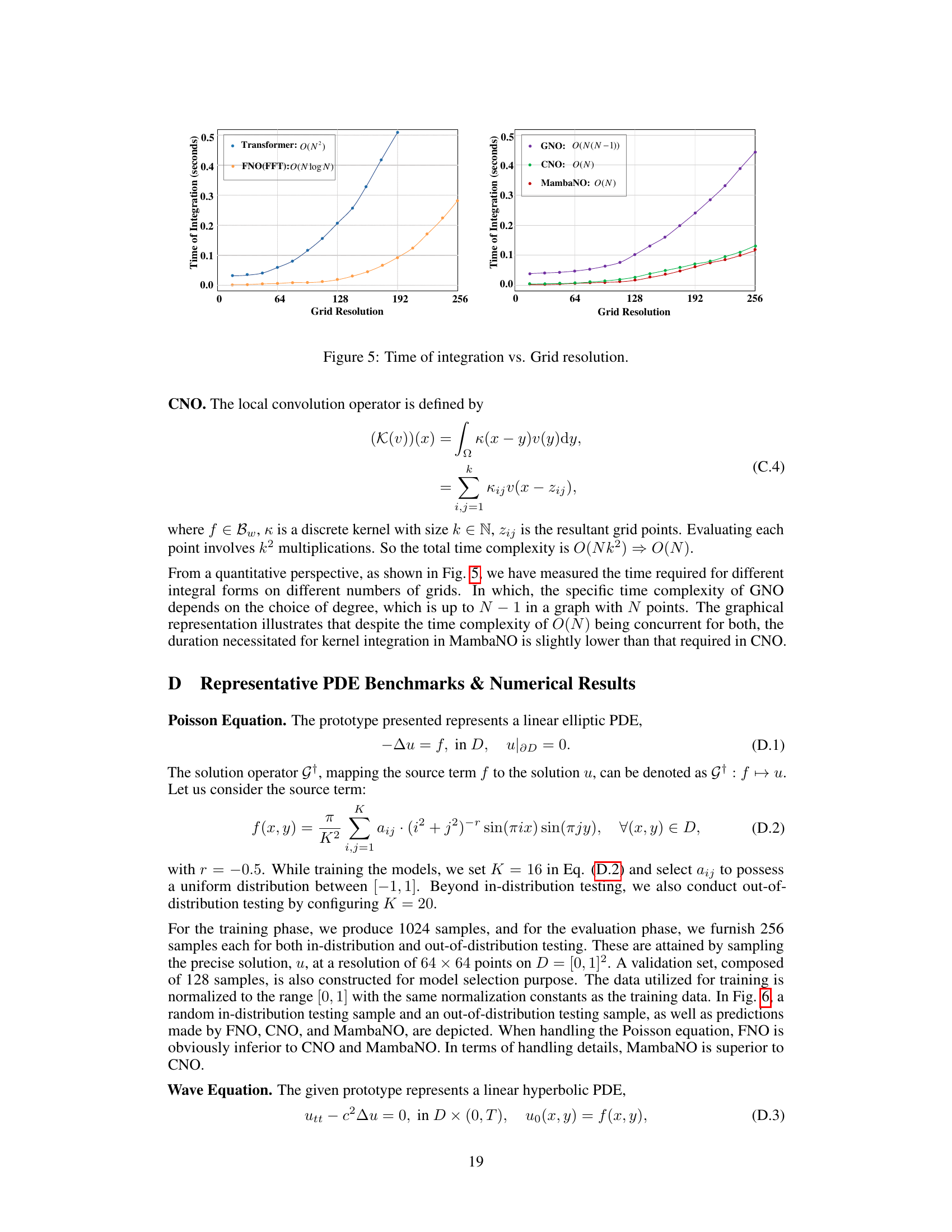
The concept of “Alias-Free MambaNO” suggests a neural operator designed for solving partial differential equations (PDEs) while addressing the issue of aliasing. MambaNO likely leverages the Mamba architecture, known for its efficiency in global information capture, but enhanced with an alias-free design to ensure accurate and consistent results across different resolutions. The “alias-free” property is crucial as it ensures that the operator’s discrete representation faithfully mirrors its continuous counterpart, thus avoiding artifacts and inaccuracies. This approach likely combines global integration (provided by the Mamba architecture) with local integration techniques (potentially convolutional layers) to effectively capture both global and local features of the PDE solution. The overall design aims for O(N) computational complexity, which represents a significant improvement in efficiency over other methods like GNO and Transformer-based operators. The improved efficiency, combined with the alias-free nature, positions MambaNO as a potentially powerful and accurate solver for PDEs, especially those with complex, multi-scale solutions.
Mamba Integration#
The proposed “Mamba Integration” method presents a novel approach to kernel integration within the neural operator framework. It leverages the efficiency of the Mamba architecture, which offers linear time complexity, O(N), to capture both global and local function features crucial for accurate PDE approximation. By cleverly combining state-space models with continuous-discrete equivalence, Mamba Integration elegantly addresses the limitations of existing kernel integration techniques which often involve computationally expensive operations like attention or global convolutions. The method’s design directly integrates with a deep learning paradigm, making it suitable for end-to-end training and deployment. Continuous-discrete equivalence is proven, ensuring reliable performance across different resolutions and avoiding aliasing errors, unlike methods like FNO. The core innovation involves reformulating the kernel integral to leverage the efficiency of the Mamba architecture while retaining crucial global information, thereby achieving a significant speed and accuracy improvement over previous approaches.
PDE Solver#
The provided text focuses on neural operators (NOs) as efficient alternatives to traditional Partial Differential Equation (PDE) solvers. NOs leverage deep learning to approximate the solution operator of a PDE, offering potential advantages in speed and robustness. The paper introduces MambaNO, a novel NO architecture designed for improved efficiency and accuracy by cleverly balancing global and local information processing. A core element of MambaNO is the use of a mamba integration technique, which aims to capture global features efficiently (O(N) complexity). This is coupled with convolutional layers to integrate local information, enhancing the model’s representational capability. The alias-free nature of MambaNO ensures stable and consistent performance across different resolutions, addressing limitations of prior NOs. MambaNO demonstrates state-of-the-art results on diverse benchmarks, suggesting its potential as a highly effective PDE solver. The approach is theoretically grounded, with proofs supporting its continuous-discrete equivalence and universal approximation capabilities. Key improvements include faster inference speeds and a reduced parameter count, compared to other deep learning-based PDE solvers. This is a significant step towards making NOs a practical and widely applicable solution for solving various PDE problems.
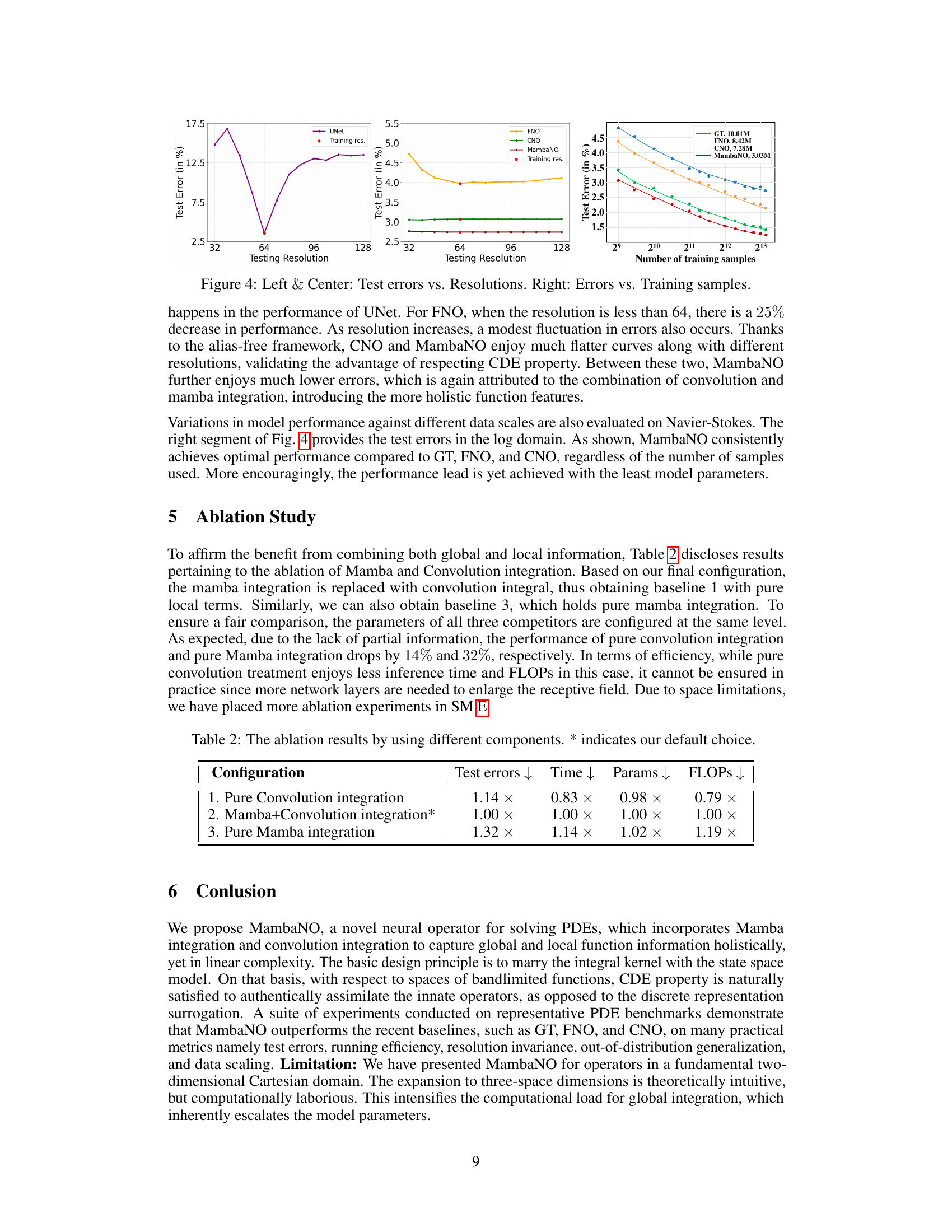
Ablation Study#
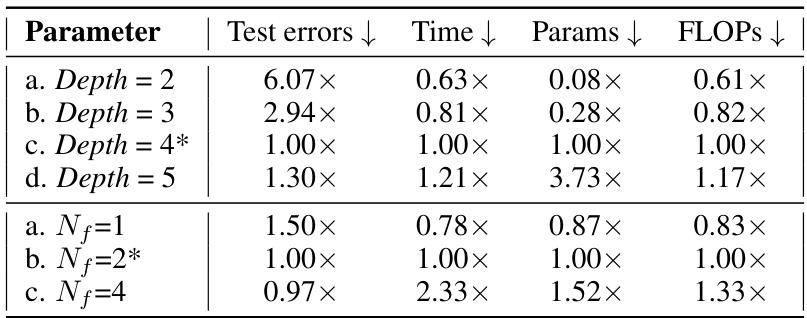
An ablation study systematically removes or deactivates components of a model to assess their individual contributions. In the context of a neural operator for solving PDEs, this might involve removing the Mamba integration, the convolutional integration, or specific layers from the network architecture. By comparing the performance of the full model against these reduced versions, researchers can quantify the impact of each component. A well-executed ablation study helps to understand the model’s design choices, justify the inclusion of particular components, and potentially identify areas for improvement or simplification. Results might show that the Mamba integration is crucial for capturing global information while the convolution provides critical local detail. Alternatively, it may reveal that certain layers are redundant, which could lead to a more efficient architecture. The findings of the study should be presented clearly, including both quantitative performance metrics (e.g., error rates) and qualitative observations about the model’s behavior. A robust ablation study is essential for establishing the validity and trustworthiness of a new model.
Future Works#
The ‘Future Works’ section of this research paper could explore several promising avenues. Extending MambaNO to higher dimensions (3D or beyond) would significantly broaden its applicability to real-world problems. This would require careful consideration of computational complexity and potential challenges in efficient global information integration. Investigating the theoretical properties of MambaNO in more detail, particularly regarding its approximation capabilities for various classes of PDEs and its robustness to noise or uncertainties in the input data, is crucial. Exploring different kernel integration techniques alongside or in lieu of mamba integration could lead to performance improvements or enhanced expressivity. This might involve a comparative analysis of convolution, attention mechanisms, or other kernel methods in conjunction with MambaNO’s state space model. Finally, applications to a wider range of scientific and engineering domains beyond those tested should be explored. The efficacy of MambaNO for problems with complex geometries, multi-scale features, or stochastic components warrants further investigation. Benchmarking against a larger suite of state-of-the-art methods would help determine the practical limits of the proposed operator learning model and inspire future improvements.
More visual insights#
More on figures

This figure shows the overall architecture of the proposed Mamba Neural Operator (MambaNO). It illustrates the multiple stages involved in processing the input function u, which undergoes multiple convolution and Mamba integrations, downsampling and upsampling operations, and finally yields an output function G(u). Each layer includes a state space model (SSM) for kernel integration, ensuring the capture of comprehensive function features, both global and local. The architecture is U-shaped, reflecting the encoder-decoder structure that maintains a balance between holistic feature representation and detailed local information.

This figure demonstrates the resolution invariance and data efficiency of the proposed MambaNO model compared to other models (UNet, FNO, CNO). The left and center panels show that MambaNO and CNO exhibit more stable performance across different resolutions compared to UNet and FNO, indicating better robustness to variations in input data resolution. The right panel illustrates that MambaNO achieves high accuracy with fewer training samples, demonstrating superior data efficiency.

This figure shows the overall architecture of the Mamba Neural Operator (MambaNO). It is a U-shaped architecture consisting of multiple layers including convolution integration, Mamba integration, downsampling, upsampling, and activation layers. The Mamba integration layer, which is a key component of MambaNO, is based on the state space model of Mamba and scans the entire function to capture global information. The convolution integration layer captures local information. The combination of these two types of integration enables MambaNO to effectively approximate operators from universal PDEs. The architecture uses a combination of convolutional layers and Mamba integration layers in a U-net like fashion with skip connections for downsampling and upsampling of the input feature map.

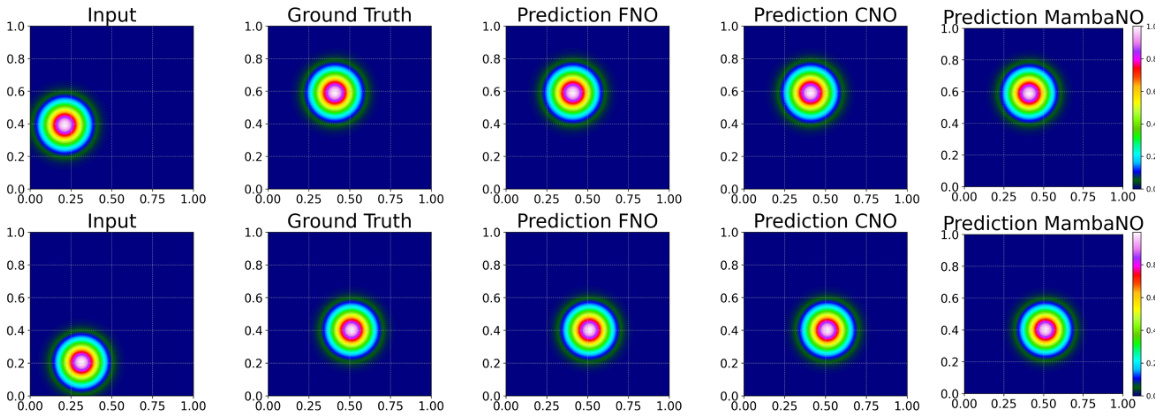
This figure shows visual comparisons of predictions made by FNO, CNO, and MambaNO on representative in-distribution and out-of-distribution examples. The top row shows in-distribution examples, and the bottom row shows out-of-distribution examples. It demonstrates the performance of each model for both in-distribution and out-of-distribution data. The visual comparison shows that MambaNO generally produces predictions closest to the ground truth, particularly in the areas marked by a black box.

This figure shows the overall architecture of the Mamba Neural Operator (MambaNO). It illustrates the different components of the model, including the convolution integration layers, Mamba integration layers, downsampling and upsampling operations, and activation functions. The figure also highlights the use of a state space model (SSM) within the Mamba integration module.
This figure shows visual comparisons of predictions made by FNO, CNO, and MambaNO on the Navier-Stokes equation for both in-distribution and out-of-distribution datasets. The top row displays in-distribution results, while the bottom row presents out-of-distribution results. Each column represents a different model’s prediction, with the ground truth in the second column. The figure visually demonstrates the superior performance of MambaNO, especially in the out-of-distribution setting, where it more closely matches the ground truth.
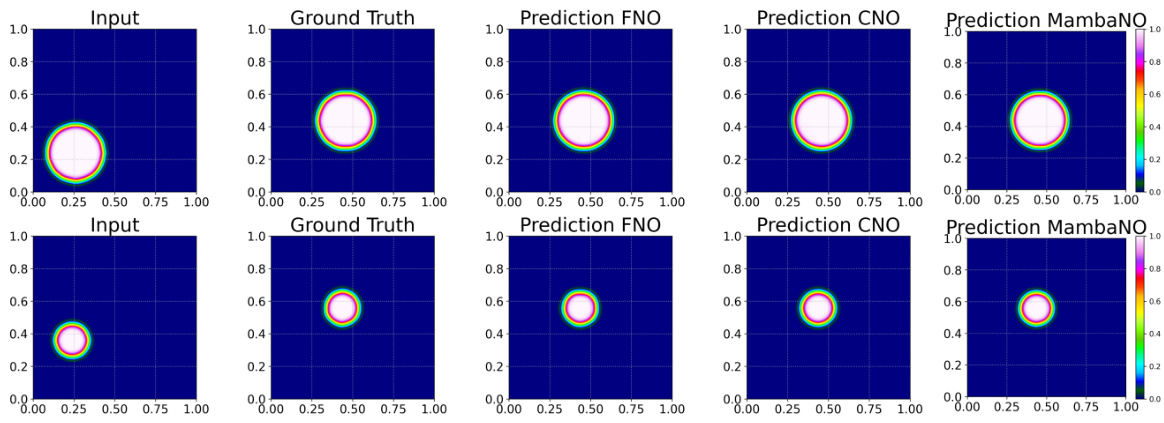
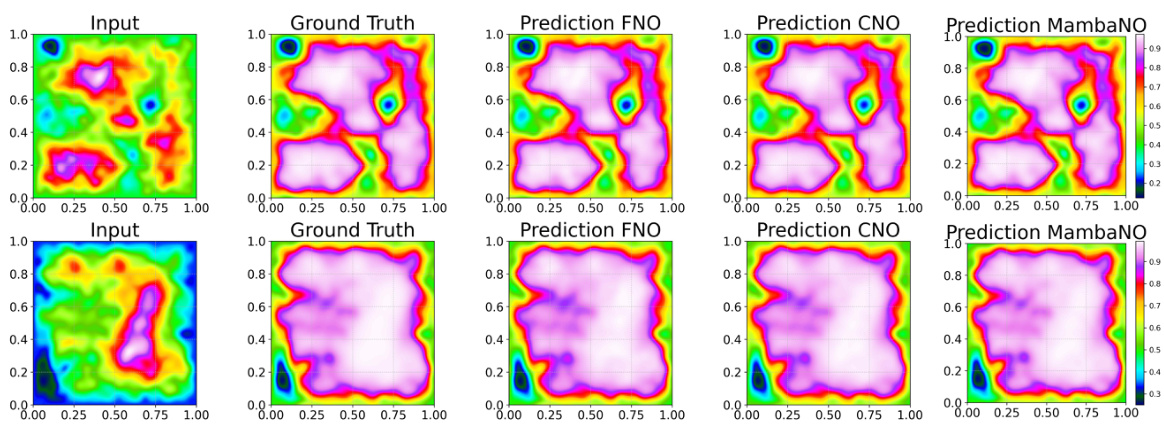
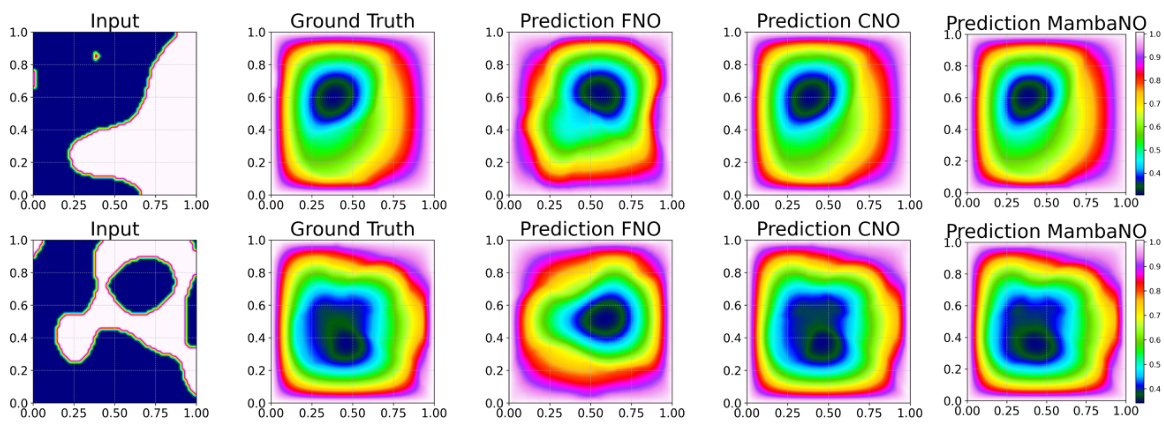
This figure shows visual comparisons of predictions made by FNO, CNO, and MambaNO on representative PDEs. The top row displays in-distribution predictions while the bottom row shows out-of-distribution predictions, highlighting the model’s ability to generalize to unseen data. The visual comparison allows for an intuitive understanding of the performance differences between the three models.
This figure presents a detailed architecture of the proposed Mamba Neural Operator (MambaNO). It illustrates the flow of data through various layers, including multiple Mamba integrations and convolutional integrations, downsampling and upsampling operations, and activation functions. The architecture shows a U-Net-like structure with skip connections, demonstrating the balance between local and global integration achieved by the model. The figure visually represents the integration of a state space model (SSM) into the neural operator architecture for efficient global information processing, combined with local convolutional layers for capturing fine-grained details in the function.
This figure shows the overall architecture of the Mamba Neural Operator (MambaNO). It’s a U-Net like architecture with several stages of downsampling and upsampling. The core components are convolutional integration layers, Mamba integration layers, and activation layers. Mamba integration is a novel technique proposed in the paper which combines local and global information from the input function.

This figure presents a detailed illustration of the Mamba Neural Operator (MambaNO) architecture. It visually outlines the distinct components and their arrangement within the model’s structure, including the sequence of convolution and Mamba integration layers, downsampling and upsampling operations, the state space model (SSM) for mamba integration, and the utilization of activation functions. This visualization effectively clarifies how the model processes data through the layers, ultimately producing the desired output. The diagram showcases the flow of information from the initial input to the final output, highlighting the key functional blocks and their interconnectedness. This is an important figure in understanding the unique design and internal workings of the proposed MambaNO.
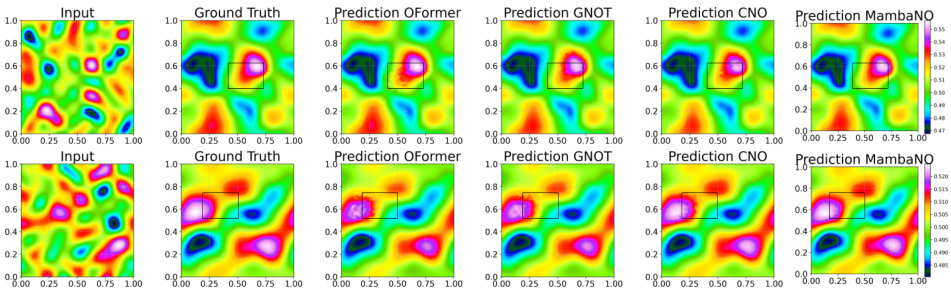
This figure shows visual comparisons of predictions made by FNO, CNO, and MambaNO on the Navier-Stokes equation for both in-distribution and out-of-distribution data. It highlights the superior performance of MambaNO in accurately capturing the complex flow patterns, particularly in the out-of-distribution cases where other methods struggle.
More on tables

This table presents the relative median L1 test errors for various PDE benchmarks (Poisson Equation, Wave Equation, etc.) across different models (GT, Unet, ResNet, DON, FNO, CNO, and MambaNO). The ‘In’ column represents the in-distribution test error, and the ‘Out’ column shows the out-of-distribution test error. It compares the performance of the proposed MambaNO against existing state-of-the-art methods for solving PDEs. Lower values indicate better performance.
This table presents the relative median L¹ test errors achieved by various models (GT, Unet, ResNet, DON, FNO, CNO, and MambaNO) across different benchmark PDEs. The ‘In’ and ‘Out’ columns indicate in-distribution and out-of-distribution test results respectively. Lower error values indicate better model performance.
This table presents the relative median L¹ test errors achieved by different machine learning models (GT, Unet, ResNet, DON, FNO, CNO, and MambaNO) on various benchmark PDEs. The performance is evaluated for both in-distribution (In) and out-of-distribution (Out) test sets. Lower values indicate better performance.

This table presents the relative median L¹ test errors achieved by different models (GT, Unet, ResNet, DON, FNO, CNO, MambaNO) on various benchmark PDEs. The table is divided into two main sections: ‘In’ (in-distribution) and ‘Out’ (out-of-distribution), indicating whether the test data was drawn from the same distribution as the training data or a different distribution. For each PDE benchmark, the table shows the relative median L¹ test error for each model. Lower values indicate better performance.

This table presents the relative median L¹ test errors achieved by different models (GT, Unet, ResNet, DON, FNO, CNO, and MambaNO) on various benchmark PDEs. The results are separated into in-distribution (In) and out-of-distribution (Out) tests. Lower values indicate better performance.

This table presents the relative median L¹ test errors achieved by different models (GT, Unet, ResNet, DON, FNO, CNO, MambaNO) on various benchmark PDEs (Poisson Equation, Wave Equation, Smooth Transport, Discontinuous Transport, Allen-Cahn Equation, Navier-Stokes Equation, Darcy Flow, Compressible Euler). The results are categorized as ‘In’ (in-distribution) and ‘Out’ (out-of-distribution) to evaluate the models’ performance under different data conditions. Lower values indicate better performance.

This table presents the relative median L¹ test errors achieved by various models (GT, Unet, ResNet, DON, FNO, CNO, and MambaNO) across different benchmark PDEs. The errors are categorized as either ‘In’ (in-distribution) or ‘Out’ (out-of-distribution), indicating whether the test data followed the same distribution as the training data. Lower values indicate better performance.
Full paper#