TL;DR#
Deep multi-agent reinforcement learning (MARL) faces challenges due to its high computational cost and numerous parameters. Existing sparse training methods have limitations in MARL because of non-stationarity and the bootstrapping nature of learning targets. This often leads to training instability and unreliable value learning.
The proposed Multi-Agent Sparse Training (MAST) framework effectively addresses these challenges. MAST incorporates the Soft Mellowmax Operator and a hybrid TD-(λ) schema to generate reliable learning targets. It also uses dual replay buffers to improve sample distribution and a gradient-based topology evolution method to train ultra-sparse networks. The results demonstrate significant reductions in redundancy and FLOPs for both training and inference across various MARL algorithms with minimal performance degradation. This significantly advances the field by making large-scale, complex MARL applications more feasible.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the significant computational cost of deep multi-agent reinforcement learning (MARL). By introducing Multi-Agent Sparse Training (MAST), it offers a practical solution to enable faster training and model compression, thereby accelerating the development and deployment of MARL systems. This is especially relevant given the increasing complexity of real-world MARL applications. The research opens up new avenues for exploring ultra-sparse network architectures and further improving the efficiency of MARL training.
Visual Insights#

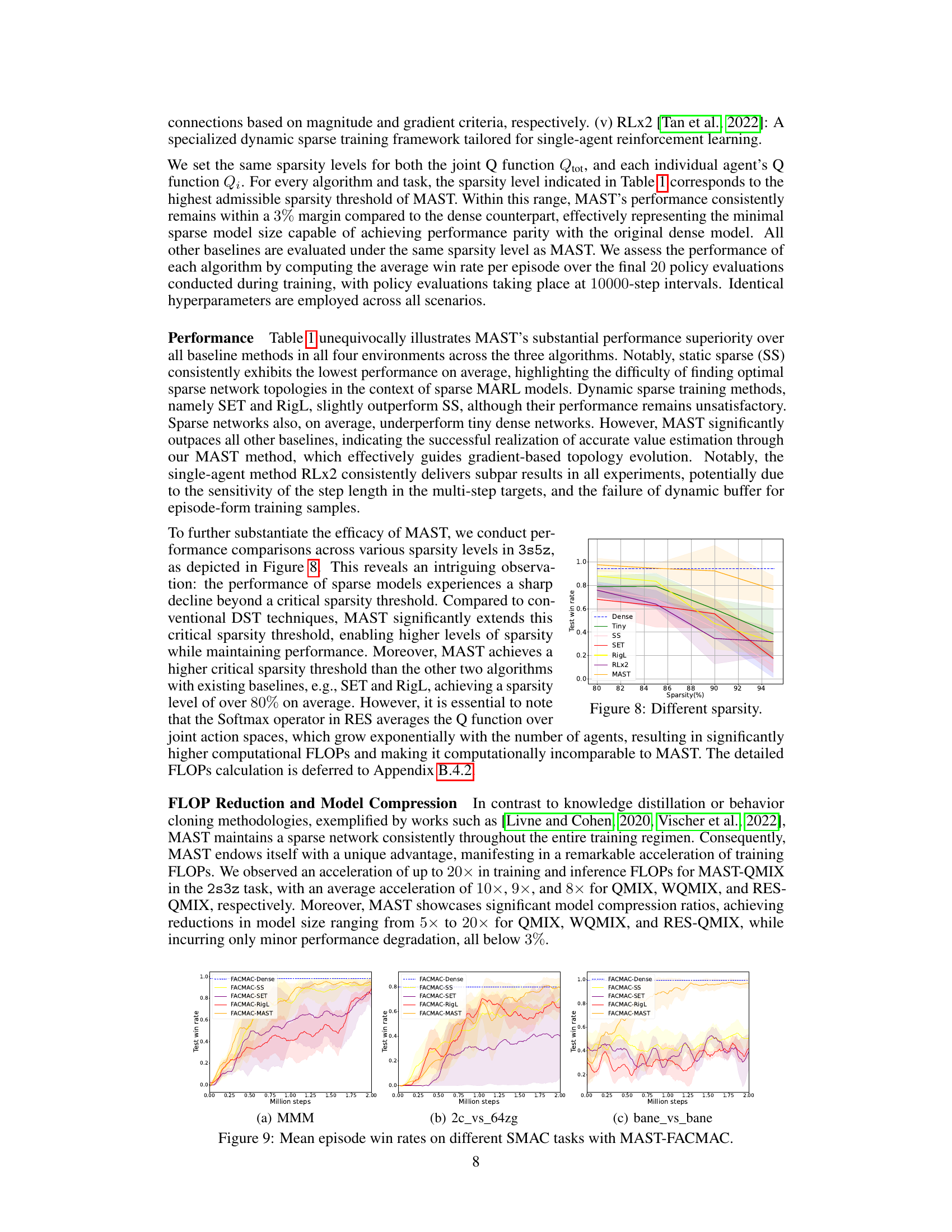
🔼 This figure compares the performance of various sparse training methods on the 3s5z task from the StarCraft Multi-Agent Challenge (SMAC) benchmark. The neural network used has only 10% of its original parameters. The methods compared include Static Sparse (SS), SET, RigL, RLx2, and the proposed MAST. The y-axis represents the win rate, illustrating MAST’s significantly superior performance compared to other methods.
read the caption
Figure 1: Comparison of different sparse training methods.

🔼 This table compares the performance of MAST against several other sparse training methods across various tasks. It shows the sparsity level, total number of parameters (normalized to the dense model), and FLOPs (training and inference, also normalized to the dense model) for each algorithm and task. It highlights MAST’s superior performance and efficiency in achieving high sparsity levels while maintaining performance close to the dense model.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.
In-depth insights#
Sparse MARL Training#
Sparse MARL training tackles the computational challenges of deep multi-agent reinforcement learning (MARL) by reducing the number of parameters in neural networks. This approach aims to improve training efficiency and model compression, making MARL more practical for large-scale applications. However, directly applying sparse training methods developed for single-agent settings often fails in MARL due to non-stationarity and the complex interplay between agents. Innovative techniques are needed to address challenges related to target reliability and the distribution of training samples. For example, using hybrid TD-learning with mellowmax operators can stabilize value estimation, while dual replay buffers can improve sample distribution, enabling reliable learning targets even with sparse networks. The effectiveness of sparse MARL training ultimately depends on carefully designed techniques that address the unique challenges of multi-agent interactions and value function approximation in a sparse parameter space. Significant FLOP reductions are a key benefit, but must be carefully balanced against potential performance degradation.
MAST Framework#
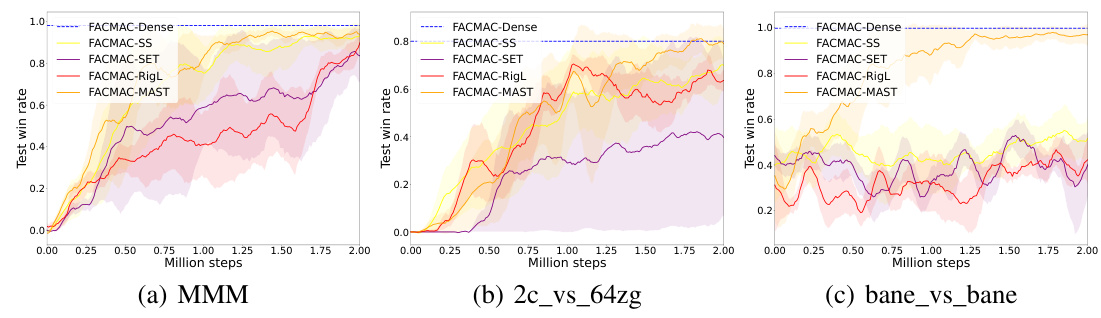
The MAST framework, designed for deep multi-agent reinforcement learning (MARL), tackles the computational challenges of training large neural networks in multi-agent scenarios. Its core innovation lies in dynamic sparse training (DST), which dynamically adjusts the network’s topology during training, thus reducing redundancy and computational cost. However, directly applying DST to MARL is problematic. MAST addresses this by incorporating several key components: a hybrid TD-(λ) learning schema that generates more reliable learning targets, a Soft Mellowmax operator to mitigate overestimation bias inherent in max-based value functions, and a dual replay buffer mechanism that improves sample distribution for enhanced stability and learning efficiency. These components, integrated within gradient-based topology evolution, allow MAST to train sparse MARL agents with minimal performance degradation, achieving significant reductions in FLOPs (floating point operations) for both training and inference. This makes the framework particularly suitable for resource-constrained environments, demonstrating significant model compression while achieving competitive performance.
Value Learning Boost#
A hypothetical ‘Value Learning Boost’ section in a multi-agent reinforcement learning (MARL) research paper would likely delve into methods for improving the efficiency and effectiveness of value function learning. This is crucial because accurate value estimations are fundamental to optimal policy learning in MARL. The discussion would likely center on addressing inherent challenges in MARL, such as non-stationarity and partial observability, which hinder efficient value learning. Specific techniques might include modifications to existing algorithms like Q-learning, perhaps incorporating novel reward shaping or bootstrapping methods. The focus would be on mitigating issues like overestimation bias, common in MARL value functions, which can lead to unstable or suboptimal policies. This might involve using techniques like double Q-learning or other advanced methods to improve the accuracy of value estimates. The ‘Value Learning Boost’ section would then analyze the impact of these methods on convergence speed, computational cost, and ultimately, the performance of the trained MARL agents. The analysis should highlight the relative effectiveness of different value learning techniques in various multi-agent scenarios and environments, presenting empirical evidence supporting the claims about performance improvements.
FLOP Reduction#
The research paper significantly emphasizes FLOP reduction as a key achievement of their proposed Multi-Agent Sparse Training (MAST) framework. MAST achieves this by employing ultra-sparse networks throughout the training process, resulting in significant reductions in Floating Point Operations (FLOPs) for both training and inference. The authors demonstrate impressive results, showcasing reductions of up to 20x in FLOPs compared to dense models across various value-based multi-agent reinforcement learning algorithms and benchmarks. This considerable reduction in computational cost is a major contribution, making the training of complex multi-agent systems more feasible and accessible. The success of MAST in achieving such significant FLOP reduction while maintaining minimal performance degradation (less than 3%) highlights the effectiveness of their approach in balancing model compression and performance. The paper also provides detailed analysis on the breakdown of FLOPs during various stages of the training process, offering valuable insights into the computational efficiency gained through MAST. The achieved FLOP reduction is not merely a quantitative metric; it represents a substantial advancement in practical applicability of value-based multi-agent reinforcement learning.
Future of Sparse MARL#
The future of sparse MARL is bright, driven by the need for efficient and scalable multi-agent systems. Research should focus on developing more sophisticated techniques for network topology optimization that go beyond simple pruning and growing, perhaps incorporating insights from graph neural networks or evolutionary algorithms. Addressing the challenges of value function approximation in sparse settings is crucial, requiring innovative methods to improve the reliability and consistency of learning targets. Hybrid approaches combining sparse and dense networks might offer performance advantages, enabling more complex tasks to be performed efficiently. Finally, further investigation into the theoretical underpinnings of sparse MARL, such as understanding the impact of sparsity on generalization and sample complexity, is essential for driving future advancements. Ultimately, sparse MARL holds great potential for deploying intelligent agents in resource-constrained environments and large-scale applications.
More visual insights#
More on figures

🔼 The figure illustrates the process of dynamic sparse training. It starts with a dense network, then randomly sparsify the network. During training, it dynamically drops and grows links based on weight magnitude and gradient information to optimize the model parameters and connectivity. This process maintains the network sparsity throughout the training with dynamic sparse training.
read the caption
Figure 2: Illustration of dynamic sparse training

🔼 This figure illustrates the MAST framework’s architecture, specifically highlighting its application within the QMIX algorithm. The framework consists of several key components: 1. Dual Buffers: An on-policy and an off-policy buffer are used for storing experience. The on-policy buffer stores the most recent experience, enhancing learning stability. The off-policy buffer stores older experience, improving sample efficiency. Both are used to sample training data. 2. Environment Interaction: Agents interact with the environment, generating experience (observations, actions, rewards). 3. Sparse MARL Agents (Agent 1 to Agent N): Multiple MARL agents are trained, each with a sparse neural network representing their Q-function (Qi). 4. Mixing Network: Combines the individual Q-functions to produce a joint action-value function (Qtot). 5. TD(λ) with Soft Mellowmax: The framework employs a hybrid TD(λ) learning target combined with the Soft Mellowmax operator to mitigate the overestimation problem that often arises in sparse network training and improve target reliability. This target is used to update the Q-functions.
read the caption
Figure 3: An example of the MAST framework based on QMIX.

🔼 This figure shows the test win rates of different step lengths of TD(λ) targets with different model sizes (sparsity levels). The x-axis represents the multi-step length and the y-axis represents the test win rate. The different lines represent different model sizes (12.5%, 10%, 7.5%, 5%). It demonstrates that an optimal step length exists for various model sizes and that the optimal step length increases as model size decreases.
read the caption
Figure 4: Performances of different step lengths.

🔼 This figure demonstrates the impact of the Soft Mellowmax operator on the performance of RigL-QMIX in the 3s5z environment of SMAC. Subfigure (a) shows the win rates, illustrating that RigL-QMIX with the Soft Mellowmax operator (RigL-QMIX-SM) outperforms the standard RigL-QMIX. Subfigure (b) displays the estimated values, highlighting that the Soft Mellowmax operator effectively mitigates overestimation bias, leading to more accurate value estimations.
read the caption
Figure 5: Effects of Soft Mellowmax operator.

🔼 The figure compares the performance of different sparse training methods on the 3s5z task from SMAC. The methods include static sparse (SS), SET, RigL, RLx2, and the proposed MAST. The y-axis represents the win rate, indicating the success rate of the trained agents. MAST demonstrates a significantly higher win rate compared to other methods, highlighting its effectiveness in multi-agent sparse training.
read the caption
Figure 1: Comparison of different sparse training methods.

🔼 This figure illustrates how the dual buffer mechanism in MAST shifts the distribution of training samples. The blue curve represents the distribution of samples from the behavior policy in a single buffer, resulting in a policy inconsistency error (d1). By using dual buffers, the distribution shifts towards the target policy (red curve), reducing the policy inconsistency error (d2). The yellow curve shows the distribution of samples from the shifted target policy.
read the caption
Figure 7: Distribution Shift: d1 and d2 are distribution distances.

🔼 This figure compares the performance of various sparse training methods on the 3s5z task from SMAC, using a neural network with only 10% of its original parameters. It shows that MAST significantly outperforms other methods such as SS, SET, RigL, and RLx2, achieving a win rate of over 90%. This highlights the challenges of applying sparse networks in MARL and demonstrates the effectiveness of the proposed MAST framework.
read the caption
Figure 1: Comparison of different sparse training methods.

🔼 This figure compares the performance of different sparse training methods on the 3s5z task from SMAC. The methods include Static Sparse (SS), SET, RigL, RLx2, and MAST. The y-axis represents the win rate, and the x-axis shows the different methods. MAST achieves a win rate of over 90%, significantly outperforming other methods.
read the caption
Figure 1: Comparison of different sparse training methods.
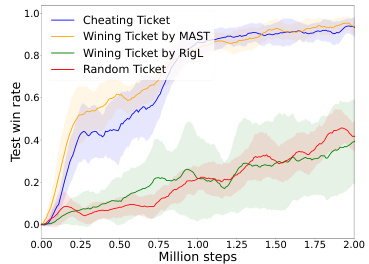
🔼 This figure compares the performance of different sparse network architectures with the same sparsity level. The ‘cheating ticket’ uses the topology obtained from MAST training and achieves the highest performance, approaching that of the dense model. The ‘winning ticket’ obtained from MAST also performs well, while both the ‘winning ticket’ from RigL and the ‘random ticket’ perform significantly worse, highlighting the effectiveness of MAST in discovering effective sparse architectures.
read the caption
Figure 10: Comparison of different sparse masks.

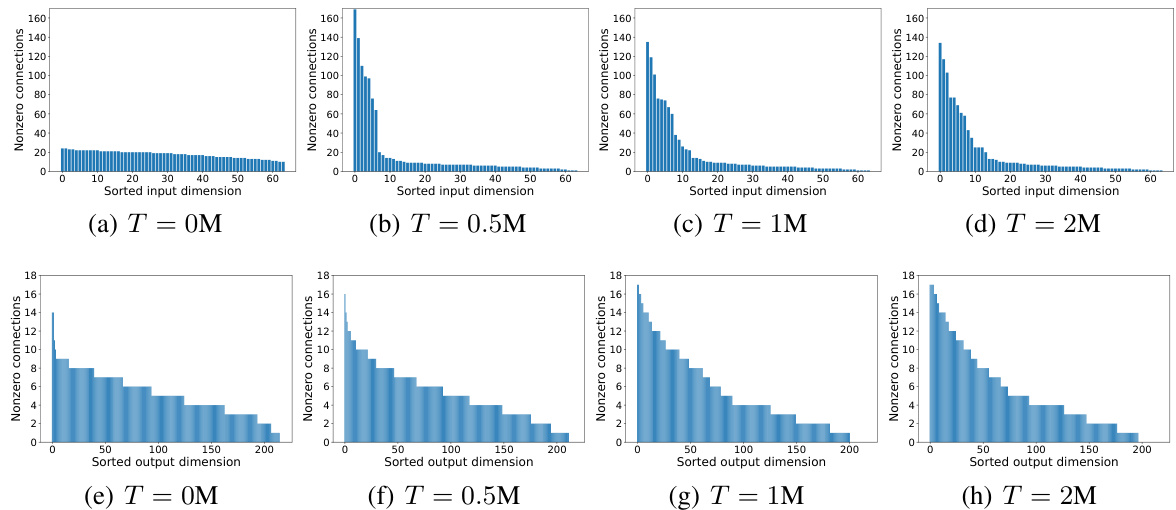
🔼 This figure visualizes the evolution of weight masks in the first hidden layer of agent 1 during the MAST-QMIX training process in the 3s5z scenario from the StarCraft Multi-Agent Challenge (SMAC) benchmark. It shows snapshots of the mask at different training steps (0M, 0.5M, 1M, and 2M), where lighter pixels indicate the presence of a connection and darker pixels represent an absent connection. The figure demonstrates how the network topology evolves during training, initially being highly sparse, gradually becoming more structured. This illustrates the dynamic sparsity of MAST and how it adapts the network structure during training.
read the caption
Figure 11: Visualization of weight masks in the first hidden layer of agent 1 by MAST-QMIX.

🔼 This figure consists of two subfigures. Subfigure (a) visualizes weight masks of the first hidden layer for different agents (stalkers and zealots) in the 3s5z scenario. It shows that the network topology for the same type of agent is very similar. However, stalkers have more connections than zealots, which is in line with their more critical roles in the game. Subfigure (b) compares the adaptive sparsity allocation scheme used in MAST with several fixed sparsity patterns (different percentage for stalkers and zealots). The results demonstrate that the adaptive sparsity allocation in MAST outperforms other manual sparsity patterns.
read the caption
Figure 12: Agent roles.
🔼 This figure compares the performance of various sparse training methods on the 3s5z task from SMAC. The methods include static sparse networks (SS), SET, RigL, RLx2, and the proposed MAST framework. The y-axis represents the win rate, showing the effectiveness of each method in achieving high performance with only 10% of the original network parameters. MAST significantly outperforms other methods.
read the caption
Figure 1: Comparison of different sparse training methods.
🔼 The figure shows the comparison of different sparse training methods on the 3s5z task from SMAC. The methods compared are Static Sparse (SS), SET, RigL, RLx2, and MAST. The y-axis represents the win rate, showing the percentage of games won by the agents trained with each method. MAST significantly outperforms all other methods, achieving a win rate of over 90%, while the other methods achieve much lower win rates. This demonstrates the effectiveness of MAST in training sparse MARL agents compared to existing sparse training methods.
read the caption
Figure 1: Comparison of different sparse training methods.
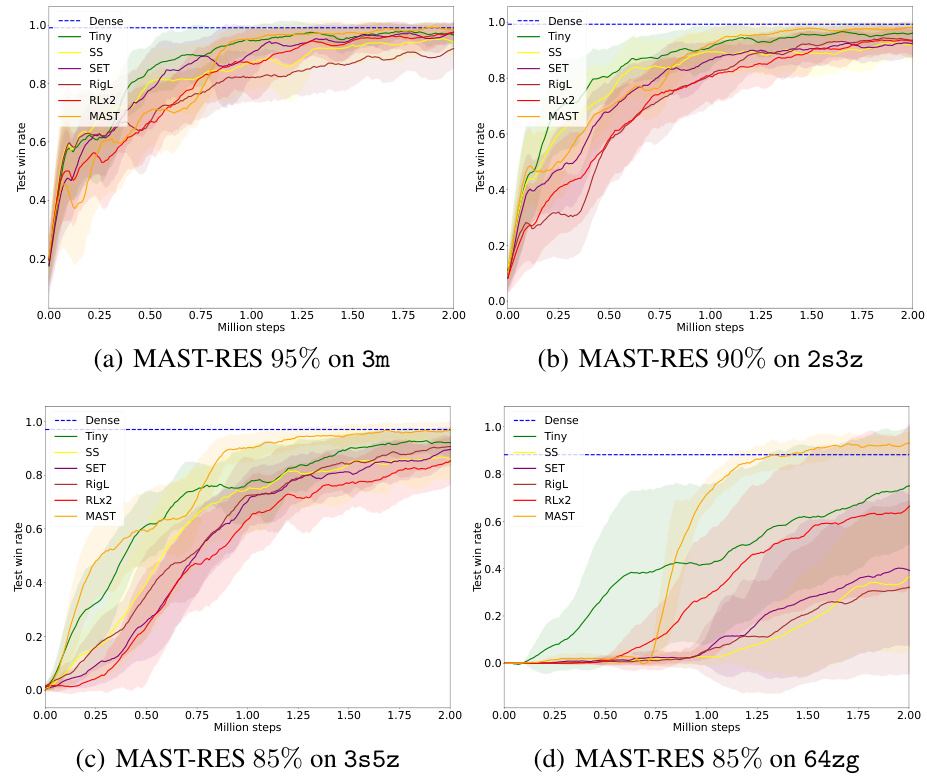
🔼 This figure compares the performance of various sparse training methods, including static sparse (SS), SET, RigL, RLx2, and the proposed MAST, on the 3s5z task from the StarCraft Multi-Agent Challenge (SMAC) benchmark. The neural network used for all methods had only 10% of its original parameters. The results show that MAST significantly outperforms the other methods, achieving a win rate of over 90%, while the others achieved win rates significantly below 50%. This highlights the challenges of applying sparse training methods directly to multi-agent reinforcement learning (MARL) and the effectiveness of the MAST framework in addressing those challenges.
read the caption
Figure 1: Comparison of different sparse training methods.
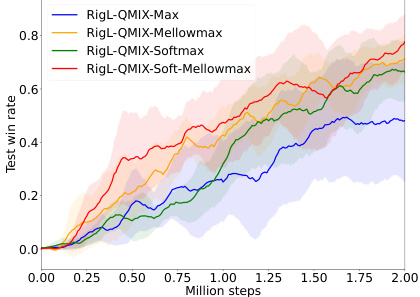
🔼 This figure shows the effects of using the Soft Mellowmax operator in the QMIX algorithm. Panel (a) displays the win rates for RigL-QMIX (without Soft Mellowmax) and RigL-QMIX-SM (with Soft Mellowmax) on the 3s5z task in SMAC. It demonstrates that RigL-QMIX-SM significantly outperforms RigL-QMIX. Panel (b) shows the estimated values for both algorithms, illustrating how the Soft Mellowmax operator effectively mitigates overestimation bias, a common problem in Q-learning.
read the caption
Figure 5: Effects of Soft Mellowmax operator.

🔼 The figure shows a bar chart comparing the performance of different sparse training methods on the 3s5z task from SMAC. The methods compared are: Static Sparse (SS), SET, RigL, RLx2, and MAST. MAST significantly outperforms the other methods, achieving a win rate of over 90%, while the others achieve win rates ranging from 32% to 49%. This highlights the effectiveness of MAST in training sparse MARL agents.
read the caption
Figure 1: Comparison of different sparse training methods.
🔼 The figure shows a bar chart comparing the performance of various sparse training methods on the 3s5z task from SMAC. The methods compared are Static Sparse (SS), SET, RigL, RLx2, and MAST. The y-axis represents the win rate, indicating the percentage of games won by the agents trained with each method. MAST significantly outperforms the other methods, achieving a win rate of over 90%, while the others achieve significantly lower win rates. This demonstrates the effectiveness of MAST in enabling the training of sparse MARL agents.
read the caption
Figure 1: Comparison of different sparse training methods.

🔼 This figure compares the performance of different sparse training methods on the 3s5z task from StarCraft Multi-Agent Challenge (SMAC). The methods compared include Static Sparse (SS), SET, RigL, RLx2 and the proposed MAST method. The y-axis represents the win rate achieved by each method, showing that MAST significantly outperforms all other methods, achieving a win rate of over 90% with a network using only 10% of its original parameters. This highlights the effectiveness of MAST in training sparse MARL agents.
read the caption
Figure 1: Comparison of different sparse training methods.

🔼 This figure visualizes the evolution of the weight mask in the first hidden layer of agent 1 during the training process of MAST-QMIX in the 3s5z scenario of the StarCraft Multi-Agent Challenge (SMAC) benchmark. The figure shows four snapshots of the weight mask at different training steps (0M, 0.5M, 1M, and 2M steps). Each snapshot represents a 64x64 matrix, where each cell represents a connection between an input neuron and an output neuron. A light pixel indicates the existence of the connection, while a dark pixel indicates the absence of a connection. The figure shows how the network’s topology changes over time, with connections becoming more concentrated in certain areas as training progresses. This visualization demonstrates the dynamic sparse training process of MAST, where the network’s topology is dynamically adjusted during training to achieve high efficiency.
read the caption
Figure 11: Visualization of weight masks in the first hidden layer of agent 1 by MAST-QMIX.
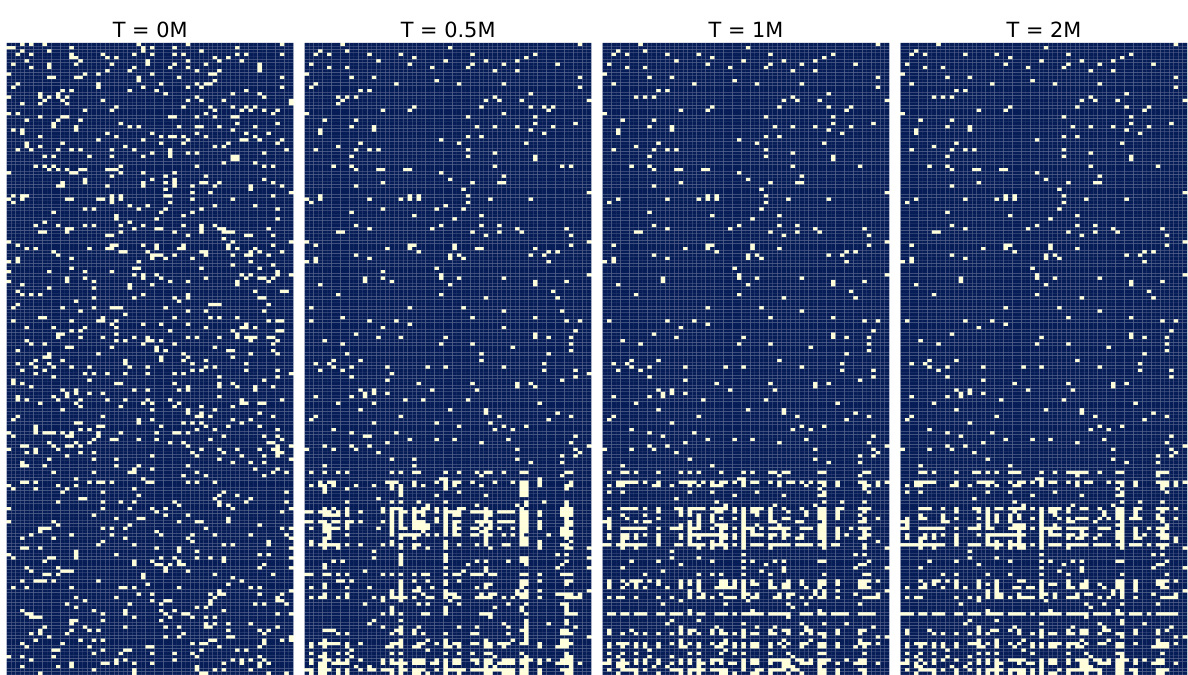
🔼 This figure visualizes the evolution of weight masks in the first hidden layer of agent 1 during the MAST-QMIX training process in the 3s5z scenario from the StarCraft Multi-Agent Challenge (SMAC) benchmark. Snapshots of the weight masks are shown at four different training steps: 0M, 0.5M, 1M, and 2M (million steps). Each mask is represented as a matrix, where a light pixel indicates the existence of a connection, and a dark pixel represents an absent connection. The figure showcases how the network’s topology evolves dynamically during training, with a pronounced shift initially and a gradual convergence of connections onto a subset of input neurons later on, highlighting the redundancy present in dense models and the efficacy of MAST in identifying essential connections.
read the caption
Figure 11: Visualization of weight masks in the first hidden layer of agent 1 by MAST-QMIX.

🔼 This figure visualizes the evolution of the weight mask in the first hidden layer of agent 1 in the MAST-QMIX model during training on the 3s5z task. The images show the sparsity pattern of the network at four different training time points (0M, 0.5M, 1M, and 2M training steps). Light pixels indicate the presence of a connection, while dark pixels represent an absent connection. The figure demonstrates how the network’s connections change over time during training, showcasing the dynamic nature of the sparse training process and the emergence of a more structured pattern from the initial random sparsity.
read the caption
Figure 11: Visualization of weight masks in the first hidden layer of agent 1 by MAST-QMIX.

🔼 The figure shows the comparison of different sparse training methods, including static sparse (SS), SET, RigL, RLx2, and MAST. MAST achieves the highest win rate (over 90%) compared to other methods on the 3s5z task from SMAC, demonstrating its effectiveness in value-based MARL. The other methods show significantly lower win rates. This highlights the challenge of applying sparse training to MARL and the unique contribution of MAST in improving both the reliability of learning targets and the rationality of sample distribution.
read the caption
Figure 1: Comparison of different sparse training methods.

🔼 The figure shows a bar chart comparing the performance of different sparse training methods on the 3s5z task from SMAC. The methods compared are Static Sparse (SS), SET, RigL, RLx2, and MAST. MAST significantly outperforms the other methods, achieving a win rate of over 90%.
read the caption
Figure 1: Comparison of different sparse training methods.
🔼 This figure compares the performance of various sparse training methods (SS, SET, RigL, RLx2, and MAST) on the 3s5z task from the StarCraft Multi-Agent Challenge (SMAC) benchmark. The neural network used in the experiment only contains 10% of its original parameters. The results demonstrate that a straightforward application of dynamic sparse training techniques such as SET and RigL, and static sparse training (SS), are ineffective in the multi-agent setting, while RLx2 is only effective for single-agent settings. In contrast, the proposed MAST framework achieves a win rate of over 90%, highlighting its effectiveness in training sparse multi-agent reinforcement learning (MARL) models.
read the caption
Figure 1: Comparison of different sparse training methods.
More on tables
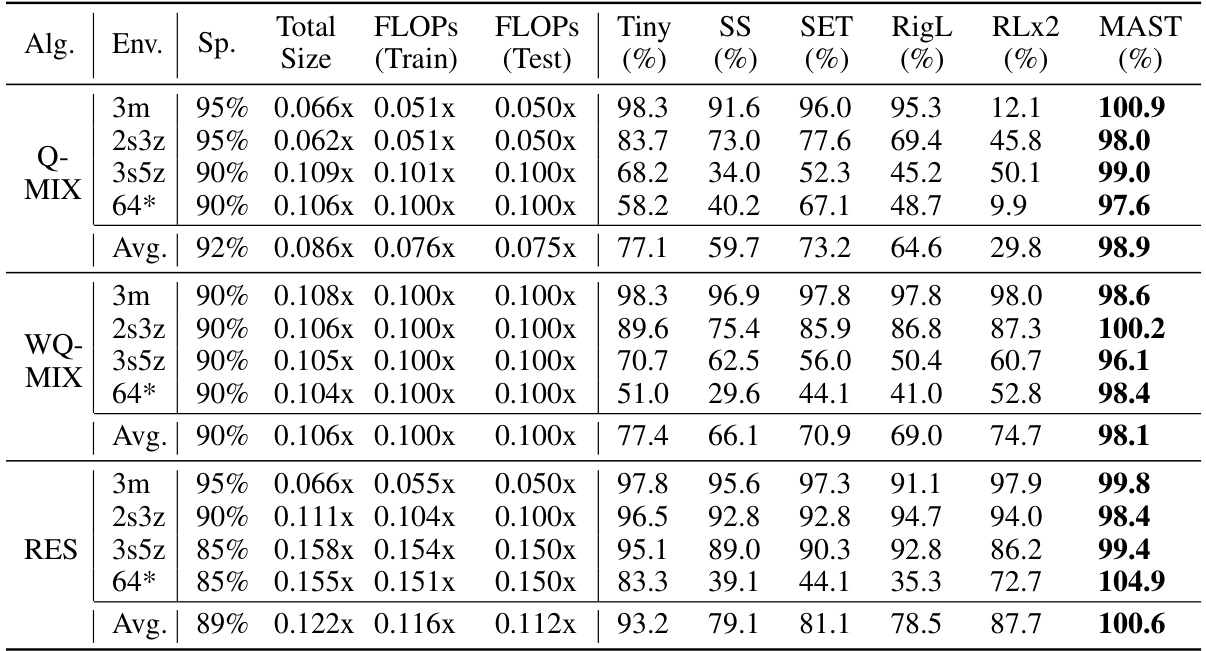
🔼 This table compares the performance of the proposed Multi-Agent Sparse Training (MAST) framework against several other sparse training baselines across four different StarCraft II environments and four different multi-agent reinforcement learning algorithms. The table shows the sparsity level, total model size, training FLOPs, testing FLOPs, and the win rate for each method. The results are normalized with respect to the dense model’s performance. It highlights MAST’s superior performance and efficiency in sparse MARL training.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.

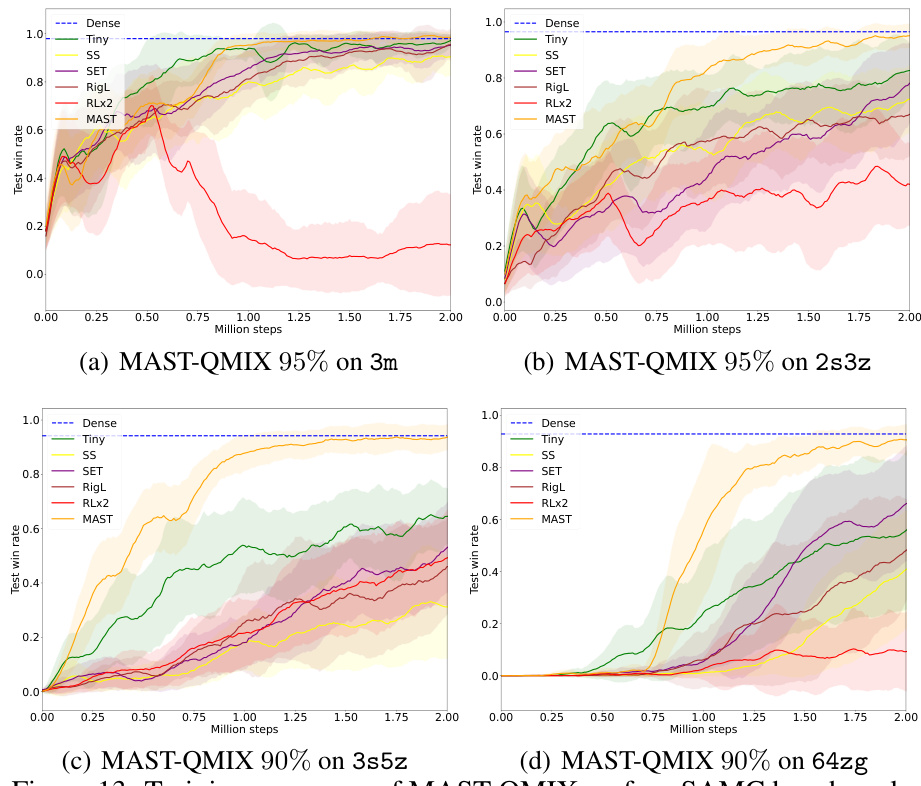
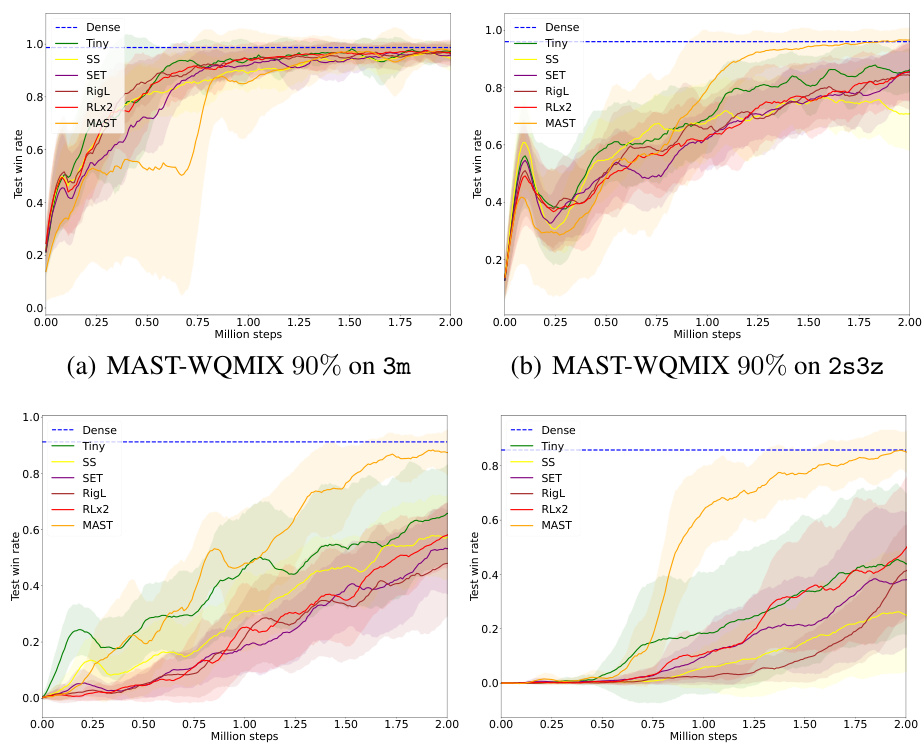
🔼 This table compares the performance of MAST against several baseline methods for different sparsity levels on various StarCraft II Multi-Agent Challenge (SMAC) environments. The baselines include using a tiny dense network, static sparse networks, other dynamic sparse training methods such as SET and RigL, and a single-agent dynamic sparse training method (RLx2). The table shows the total size, training FLOPs, and inference FLOPs of each method, along with their test win rates (normalized against the dense network) on various SMAC maps.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.

🔼 This table compares the performance of MAST against several baseline methods across various tasks in the StarCraft Multi-Agent Challenge (SMAC) benchmark. The table shows the sparsity level (percentage of parameters pruned), the total number of parameters (normalized to the dense model), and the final performance (win rate) achieved by each method, including MAST, Tiny (a small dense model), SS (static sparsity), SET, RigL, RLx2 (single-agent dynamic sparsity). Results demonstrate the superior performance of MAST over other baseline methods in different scenarios, and across different MARL algorithms like QMIX, WQMIX, and RES.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.
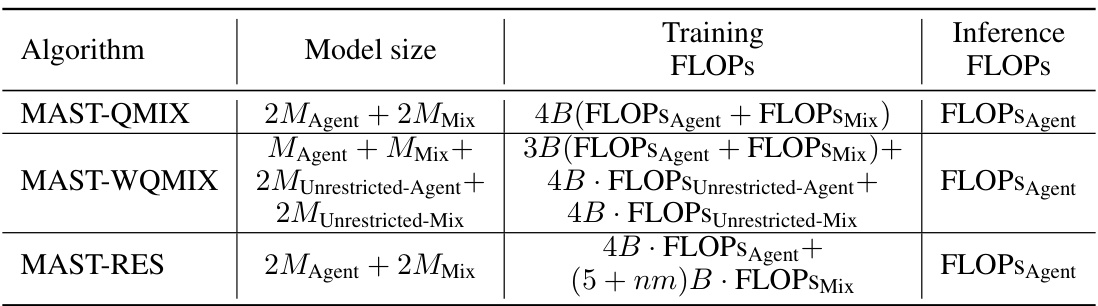
🔼 This table compares the performance of the proposed MAST framework against various baseline methods for different sparsity levels across several environments from the StarCraft Multi-Agent Challenge (SMAC) benchmark. It shows the total size, training FLOPS, inference FLOPS, and win rates for each algorithm and environment. The sparsity levels tested are shown in the Sp. column, and the results are normalized to the dense model’s performance.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.

🔼 This table compares the performance of MAST against various baseline sparse training methods across multiple SMAC environments and different value-based MARL algorithms. The ‘Sp.’ column indicates the sparsity level used, while ‘Total Size’ represents the total number of model parameters. The FLOPs (floating point operations) for training and inference are also shown, normalized against the dense model. The results highlight MAST’s significant performance improvement over other methods, even with high sparsity levels.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.

🔼 This table compares the performance of MAST against several baseline methods (Tiny, SS, SET, RigL, RLx2) across four different SMAC environments (3m, 2s3z, 3s5z, 64zg) and three different MARL algorithms (QMIX, WQMIX, RES). For each algorithm and environment, the table shows the sparsity level achieved (Sp.), the total size of the sparse model (Total Size), and the win rate achieved in percentage for each method. The results demonstrate the superior performance of MAST compared to the other methods, especially in terms of achieving high win rates while maintaining a high level of sparsity.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.

🔼 This table compares the performance of MAST against several baseline methods for different sparsity levels on various SMAC benchmark environments. The baselines include using tiny dense networks, static sparse networks, and dynamic sparse training methods like SET and RigL. The table shows the total size (number of parameters), training FLOPs, and inference FLOPs, all normalized relative to the dense model. The ‘Sp.’ column indicates the sparsity level used for each method and environment. The results demonstrate that MAST outperforms baseline methods, achieving minimal performance degradation with significantly reduced FLOPs.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.

🔼 This table compares the performance of the proposed Multi-Agent Sparse Training (MAST) framework against several baseline methods across various tasks in the StarCraft Multi-Agent Challenge (SMAC) benchmark. The performance metric is the win rate, with sparsity levels ranging from 85% to 95%. The table shows the total model size (in terms of parameters), and training and inference FLOPs, all normalized relative to a dense model. This demonstrates the model compression and computational efficiency gains achieved by MAST compared to other approaches such as static sparse networks (SS), SET, RigL, and RLx2.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.

🔼 This table compares the performance of MAST against various baseline methods for sparse training in multi-agent reinforcement learning. It shows the sparsity level (percentage of parameters retained), total number of parameters (normalized to the dense model), and performance (win rate) for different algorithms and environments in the StarCraft Multi-Agent Challenge (SMAC) benchmark. The baseline methods include Tiny (a small dense model), SS (static sparse network), SET (Sparse Evolutionary Training), RigL (a dynamic sparse training method), and RLx2 (a dynamic sparse training method for single-agent RL). The results demonstrate that MAST outperforms other sparse training methods by achieving high win rates while maintaining a high level of sparsity.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.

🔼 This table compares the performance of MAST against various baseline methods for different sparsity levels across four different StarCraft II environments. The baselines include training tiny dense networks, using static sparse networks, employing dynamic sparse training with SET and RigL, and using a dynamic sparse training framework from single agent RL (RLx2). The table shows the total size (number of parameters), training FLOPs, and testing FLOPs of the models, normalized by the dense model. The ‘Sp.’ column shows the sparsity level (%) of each method and environment. The results demonstrate that MAST achieves significantly higher performance compared to the baseline methods, while maintaining a high level of sparsity.
read the caption
Table 1: Comparisons of MAST with different sparse training baselines: 'Sp.' stands for 'sparsity', 'Total Size' means total model parameters, and the data is all normalized w.r.t. the dense model.
Full paper#