TL;DR#
Deep learning’s success with overparameterized models like ConvResNets lacks theoretical grounding. Existing theories require model sizes smaller than sample sizes, contrasting real-world applications where models are vastly larger. This restricts existing understanding and hinders the development of improved models. This paper addresses these issues by focusing on ConvResNeXts, a generalization of ConvResNets.
This research analyzes ConvResNeXts using nonparametric classification theory. They assume a smooth target function exists on a low-dimensional manifold within a high-dimensional space – a realistic scenario for many datasets. The key finding is that ConvResNeXts, even with far more parameters than data points, effectively learn these functions without suffering from the ‘curse of dimensionality’, a common issue in high-dimensional settings. This is achieved through weight decay implicitly enforcing sparsity within the network’s structure.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides a theoretical understanding of why overparameterized convolutional neural networks (ConvResNets) perform well, addressing a major gap in deep learning theory. It offers novel insights into architectural choices like residual connections and parallel blocks, paving the way for more efficient and effective model designs. This work is highly relevant to current trends in deep learning, particularly in addressing overparameterization and the curse of dimensionality. It opens new avenues for research in nonparametric classification and the theoretical analysis of deep learning models.
Visual Insights#
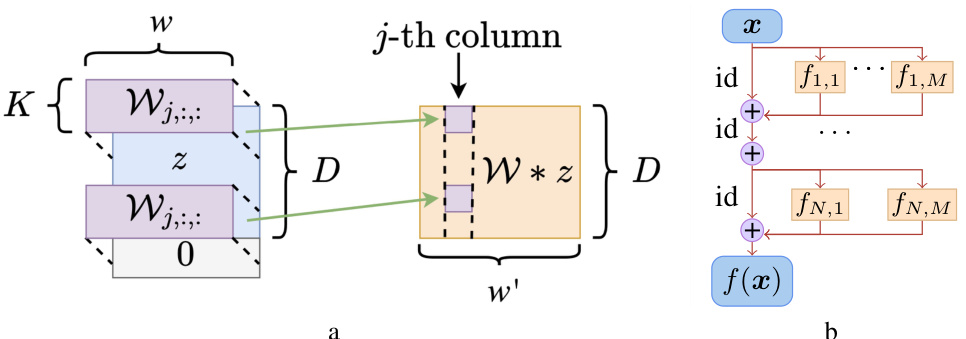
🔼 Figure 1(a) shows a 1D convolution operation where a kernel W of size K convolves with an input vector z of length D and width w to produce an output vector of length D and width w’. Figure 1(b) shows the architecture of a ConvResNeXt network consisting of N residual blocks. Each residual block contains M parallel blocks, each being a small convolutional neural network.
read the caption
Figure 1: (a) Demonstration of the convolution operation W * z, where the input is z ∈ RD×w, and the output is W * z ∈ RD×w'. Here Wj,:,: is a D × w matrix for the j-th output channel. (b) Demonstration of the ConvResNeXt. f1,1 ··· fN,M are the building blocks, each building block is a convolution neural network.
In-depth insights#
Overparam. Benefits#
Overparameterization, where the number of model parameters exceeds the size of the training dataset, presents a paradox in machine learning. While intuitively counterintuitive, it demonstrably enhances performance. This paper’s analysis suggests that overparameterization, when coupled with weight decay regularization, implicitly promotes sparsity within the network. This sparsity, combined with the specific architectural properties of convolutional residual networks (ConvResNets), enables the model to efficiently learn complex functions defined on low-dimensional manifolds, mitigating the curse of dimensionality. The success hinges on ConvResNets’ ability to adapt to both the function’s smoothness and the underlying low-dimensional structure of the data. This contrasts with traditional models that often struggle with high-dimensional data. Therefore, the advantages observed are not merely due to increased model flexibility alone, but rather a synergistic effect of overparameterization, regularization, and the network architecture itself.
ConvResNeXt Theory#
The ConvResNeXt theory section likely delves into the mathematical underpinnings of the ConvResNeXt architecture, explaining its ability to achieve strong performance, particularly in the context of overparameterization. The authors likely explore its approximation capabilities, demonstrating how ConvResNeXts can effectively approximate complex functions even with more parameters than training data points. Key aspects likely include generalization bounds, showing that despite overparameterization, the model does not overfit but generalizes well to unseen data. Analysis of the weight decay mechanism is crucial; the authors likely show how it implicitly enforces sparsity, preventing overfitting and potentially contributing to the network’s generalization power. Furthermore, the theory section could address the network’s ability to learn low-dimensional structures and adapt to the smoothness of target functions on manifolds, mitigating the curse of dimensionality. Overall, this section aims to theoretically ground the empirical success of ConvResNeXts, offering a compelling explanation for its performance.
Manifold Assumption#
The manifold assumption, a cornerstone of many dimensionality reduction and machine learning techniques, posits that high-dimensional data often lies on or near a low-dimensional manifold embedded in the high-dimensional space. This assumption is crucial because it suggests that the intrinsic dimensionality of the data is much lower than its ambient dimensionality. This allows for efficient learning and analysis by focusing on the lower-dimensional structure, thus mitigating the curse of dimensionality. The manifold assumption is particularly relevant in the context of image classification, where images can be considered as points in a high-dimensional space representing pixel values. However, the manifold assumption is not without limitations. Determining the true dimensionality of the manifold and its geometric properties can be challenging, and the assumption might not hold for all datasets. Furthermore, the success of manifold-based methods relies heavily on the choice of appropriate algorithms and parameters. Despite its limitations, the manifold assumption offers a powerful framework for understanding and analyzing high-dimensional data, allowing for the development of computationally efficient and effective machine learning models.
Adaptivity Analysis#
An adaptivity analysis in a machine learning context would rigorously examine how well a model adjusts to various data characteristics. This involves investigating the model’s ability to learn diverse patterns effectively, and exploring how model parameters interact to achieve this flexibility. A key aspect is assessing the model’s generalization performance across unseen datasets; a truly adaptive model should seamlessly transfer its learned knowledge without significant performance degradation. Efficiency is another crucial consideration; a highly adaptive model should achieve its performance goals without an excessive computational burden. The analysis would likely involve controlled experiments with varying data distributions, parameter settings, and model architectures. The ultimate goal is to understand the model’s strengths and weaknesses, thus optimizing the model for optimal adaptivity.
Future Directions#
Future research could explore the generalizability of these findings to a wider range of datasets and architectures. Investigating the impact of different hyperparameters, such as the depth and width of the network, on the performance of overparameterized ConvResNeXts, and comparing their generalization properties to those of other architectures like transformers would provide valuable insights. Further theoretical work is needed to fully understand the role of weight decay in ensuring the generalization properties of these models, perhaps exploring different regularization techniques. Finally, practical applications of this research to real-world scenarios, including transfer learning and domain adaptation, will further confirm the usefulness of overparameterized networks for various tasks. More importantly, the connection between the model’s architecture and the intrinsic dimension of the data should be further investigated and potentially used to guide the design of future architectures.
More visual insights#
More on figures

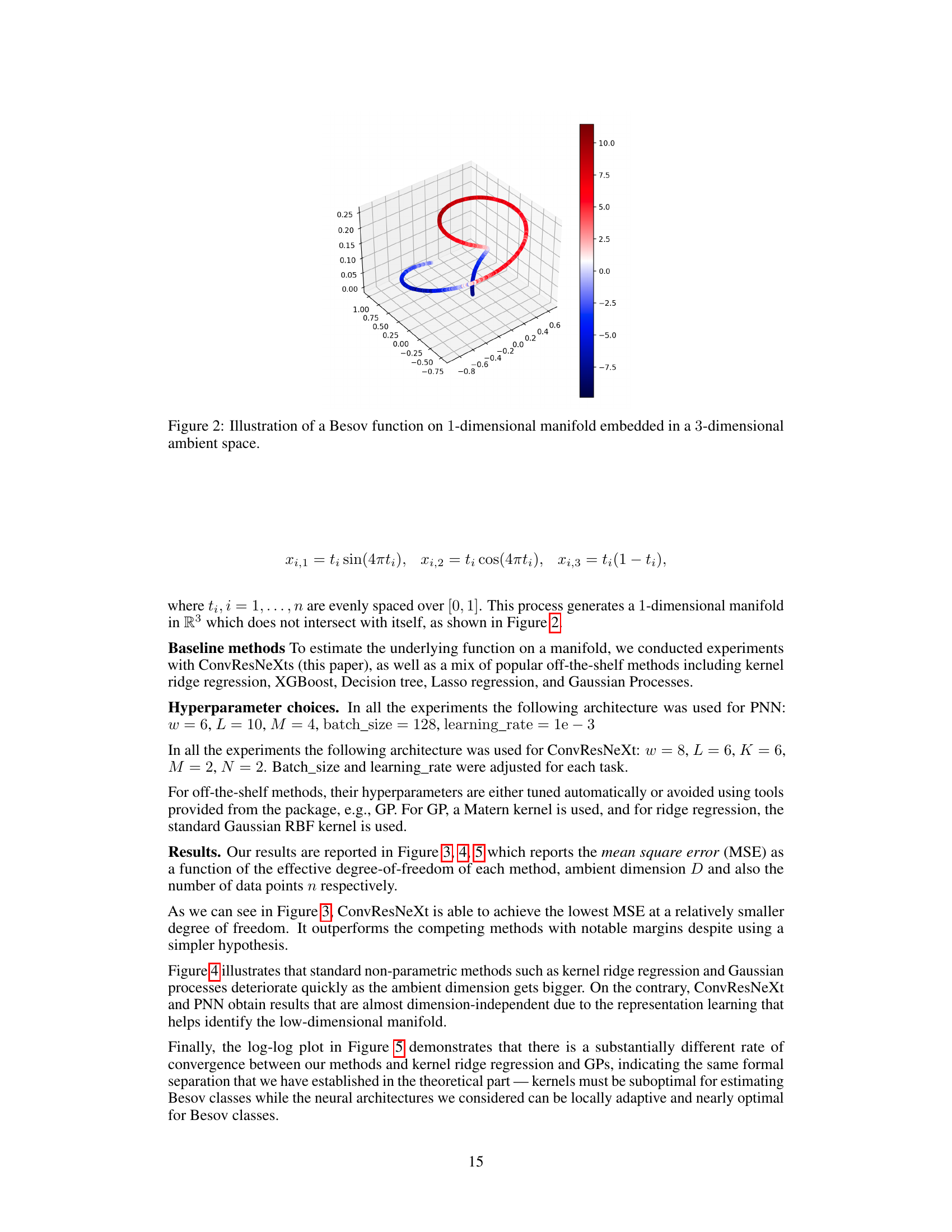
🔼 The figure visualizes a Besov function defined on a one-dimensional manifold that is embedded within a three-dimensional ambient space. The manifold itself is a curve that resembles a twisted loop. The color coding represents the function’s values along the manifold, ranging from negative (blue) to positive (red). The visualization demonstrates how a relatively simple function (one-dimensional) can have a complex appearance when viewed within a higher-dimensional setting.
read the caption
Figure 2: Illustration of a Besov function on 1-dimensional manifold embedded in a 3-dimensional ambient space.

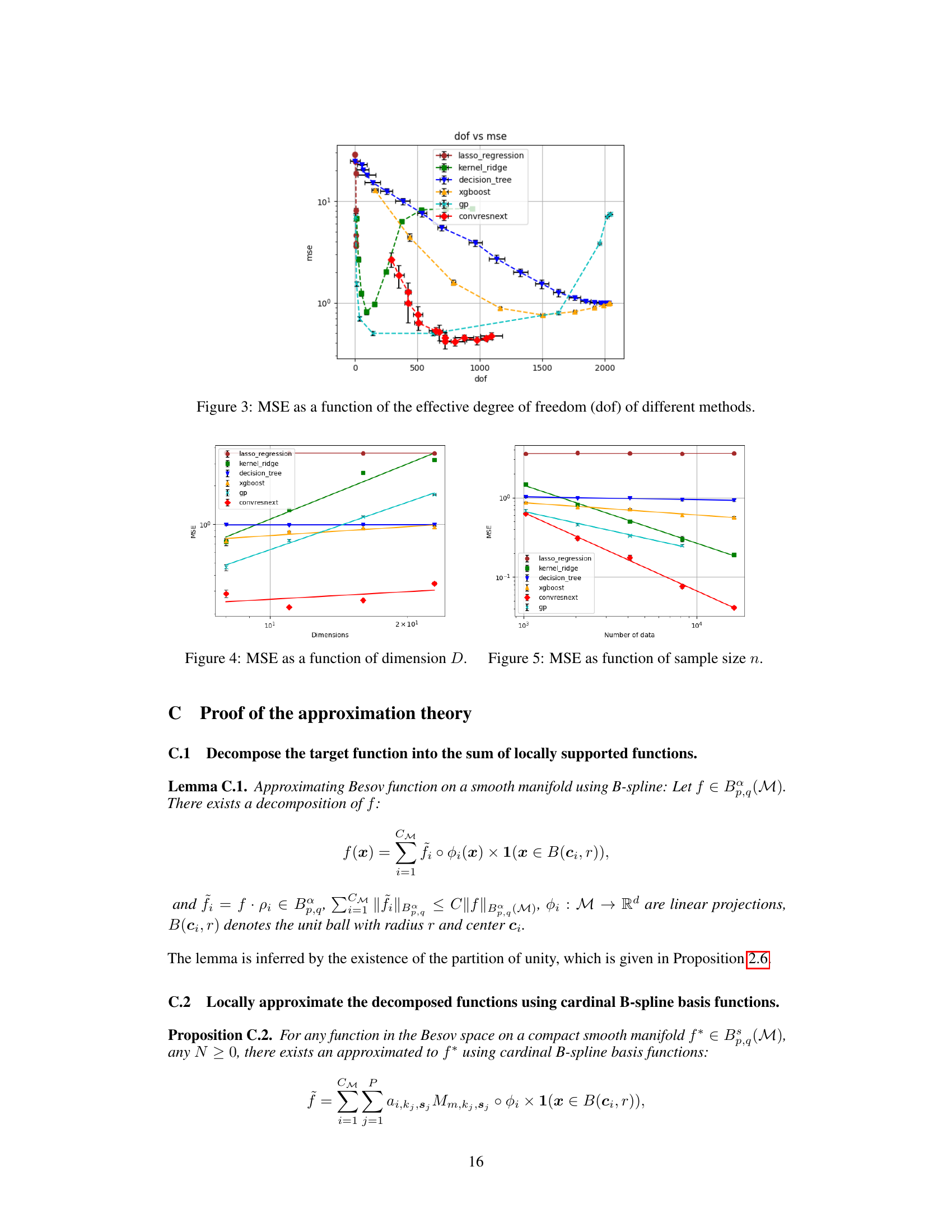
🔼 This figure compares the mean squared error (MSE) achieved by various regression methods as a function of their effective degrees of freedom. It shows that ConvResNeXt achieves the lowest MSE with a relatively smaller number of degrees of freedom compared to other methods like Lasso regression, kernel ridge regression, decision trees, XGBoost, and Gaussian Processes. This suggests that ConvResNeXt is more efficient and effective for this task.
read the caption
Figure 3: MSE as a function of the effective degree of freedom (dof) of different methods.

🔼 This figure shows the mean squared error (MSE) of different regression models plotted against the ambient dimension (D) of the data. It demonstrates the effect of increasing data dimensionality on the accuracy of various methods, including ConvResNeXt (our proposed method), Kernel Ridge Regression, Lasso Regression, XGBoost, Decision Tree, and Gaussian Processes. The results highlight the relative robustness of ConvResNeXt and PNN to increasing dimensionality compared to the other methods. Specifically, ConvResNeXt and PNN show much smaller increases in MSE as D increases compared to other baselines.
read the caption
Figure 4: MSE as a function of dimension D.
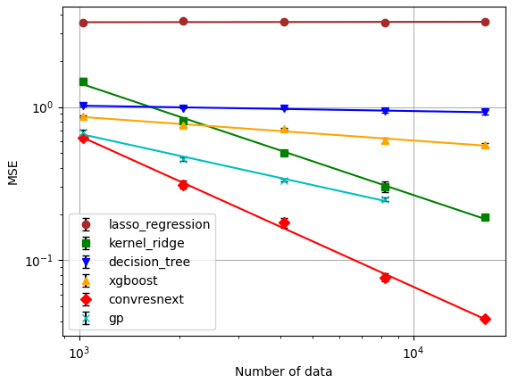
🔼 This figure displays the mean squared error (MSE) for various regression methods plotted against the number of data points (n). It shows how the MSE changes as the amount of training data increases. The different lines represent different regression techniques, illustrating their comparative performance and scalability with data size.
read the caption
Figure 5: MSE as function of sample size n.
Full paper#