TL;DR#
Many real-world decision-making problems involve multiple conflicting objectives. Existing multi-armed bandit algorithms often struggle to handle these situations efficiently. Preference-based Pure Exploration (PrePEx) aims to solve this challenge by incorporating preferences over objectives, but efficient algorithms for PrePEx were lacking. This leads to a computationally expensive drug discovery process.
This paper introduces the Preference-based Track and Stop (PreTS) algorithm to address this problem. PreTS provides a convex relaxation of the lower bound on sample complexity, leading to a computationally efficient algorithm. The authors prove that PreTS’s sample complexity is asymptotically optimal, offering a significant advancement in handling multi-objective decision-making under uncertainty.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in multi-armed bandits and vector optimization. It offers a novel lower bound and a tight algorithm for preference-based pure exploration, addressing a critical gap in existing research. The geometric insights and convex relaxation techniques are valuable for tackling complex optimization problems beyond the scope of this specific problem.
Visual Insights#
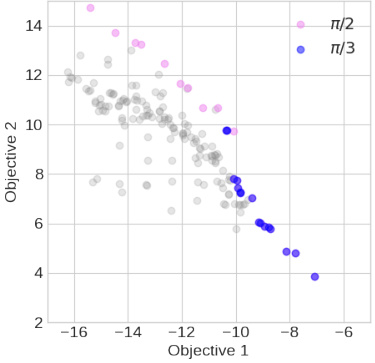
🔼 This figure shows how the choice of the preference cone affects the Pareto optimal set. The Pareto optimal sets for two different cones, Cπ/2 and Cπ/3, are shown in pink and blue, respectively. The grey points represent the reward vectors of 200 randomly selected arms. The figure illustrates that the geometry of the preference cone significantly impacts the size and composition of the Pareto optimal set.
read the caption
Figure 1: Effect of cone selection on size of Pareto optimal set
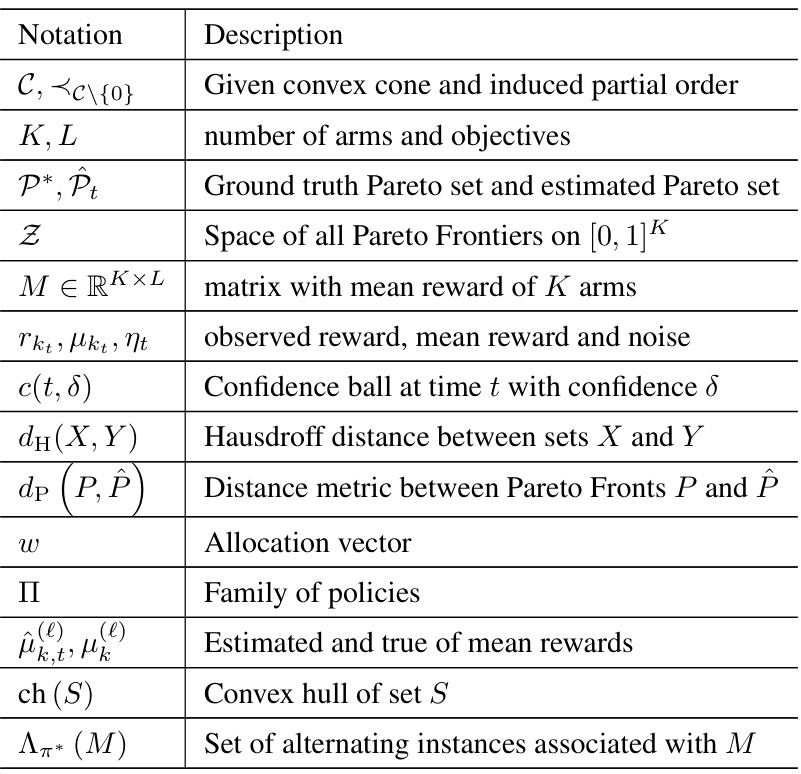
🔼 This table lists notations used throughout the paper. It includes mathematical symbols representing concepts such as the ordering cone, number of arms and objectives, Pareto sets, the reward matrix, rewards, confidence balls, distances between Pareto fronts, allocation vectors, families of policies, and estimated/true mean rewards, among others. These notations are crucial for understanding the mathematical formulations and algorithms presented in the paper.
read the caption
Table 1: Table of Notations
Full paper#



















