TL;DR#
Many downstream applications using diffusion models require sampling from complex posterior distributions, a computationally challenging task. Existing methods often provide only approximate solutions or are limited to specific cases. This paper tackles this challenge by proposing a novel data-free learning objective called “Relative Trajectory Balance” (RTB) for training diffusion models to sample from arbitrary posteriors. The method is rooted in viewing diffusion models as generative flow networks.
RTB is proven to be asymptotically correct and leverages deep reinforcement learning for improved mode coverage. Experimental results across diverse domains including vision, language, and offline reinforcement learning demonstrate RTB’s versatility and superior performance compared to existing techniques. The paper showcases unbiased posterior inference and achieves state-of-the-art results in offline reinforcement learning, highlighting the broader implications of RTB for various fields.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with diffusion models, particularly in tackling intractable inference problems. It offers a novel, asymptotically unbiased training objective, relative trajectory balance (RTB), enabling efficient posterior sampling. The versatility across diverse domains (vision, language, control) and state-of-the-art results in offline reinforcement learning make this a significant contribution with broad applicability and inspire future research on unbiased inference.
Visual Insights#

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The goal is to sample from a posterior distribution that is a product of a prior (mixture of 25 Gaussians) and a constraint (masking all but 9 modes). The figure shows that the proposed Relative Trajectory Balance (RTB) method accurately samples from the posterior, while other methods like Reinforcement Learning (RL) with and without KL regularization, and Classifier Guidance (CG) either fail to accurately estimate or mode collapse.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This table summarizes four different applications of diffusion models where downstream tasks require sampling from product distributions that involve a pretrained diffusion model as a prior and an auxiliary constraint. It outlines the specific diffusion model prior used in each domain (vision, language, and reinforcement learning), the type of constraint applied, and the resulting posterior distribution that is the target of the sampling. This table helps to illustrate the wide applicability of the proposed method and how it addresses the intractable posterior inference problem across diverse tasks.
read the caption
Table 1: Sources of diffusion priors and constraints.
In-depth insights#
Diffusion Posterior#
The concept of “Diffusion Posterior” integrates diffusion models with Bayesian inference to address posterior estimation challenges. Diffusion models excel at generating samples from complex probability distributions, but directly sampling from a target posterior often proves computationally intractable. The core idea is to leverage the generative power of diffusion models as priors, while incorporating constraint or likelihood functions to guide the sampling towards the desired posterior distribution. This approach offers a compelling alternative to traditional inference methods, particularly in scenarios with high-dimensional data and intricate posterior landscapes. Key challenges include efficient posterior sampling algorithms, and rigorous theoretical analysis to ensure the asymptotic correctness and unbiasedness of the estimated posterior. Further research should focus on developing more scalable and robust methods for training and inference, while exploring various applications across diverse fields.
RTB Training#
RTB (Relative Trajectory Balance) training offers a novel approach to learning diffusion models for posterior sampling. Instead of relying on approximations or computationally expensive methods, RTB leverages a data-free learning objective based on the generative flow perspective. This allows for unbiased inference of arbitrary posteriors under diffusion priors, a significant improvement over existing methods. The core idea is to train a diffusion model to match a target posterior distribution, which is intractable. This is achieved by minimizing the discrepancy between the trajectories sampled from the trained model and those expected from the target distribution, weighted by the constraint function. Off-policy training is enabled, increasing the flexibility and efficiency of the learning process. The framework is applicable across various domains, demonstrated by the results in vision, language, and control tasks. Asymptotic correctness is proven for RTB, providing a theoretical foundation for its effectiveness. While requiring careful hyperparameter tuning and potentially suffering from high variance gradients due to the reliance on whole trajectories, RTB offers a potentially powerful technique for exact posterior sampling in diffusion models.
Empirical Results#
An ‘Empirical Results’ section in a research paper would present the findings of experiments conducted to test the paper’s hypotheses or claims. A strong section would clearly present the experimental setup, including datasets used and any preprocessing steps. Quantitative results should be reported with appropriate statistical significance measures (e.g., error bars, p-values) to demonstrate reliability and avoid spurious conclusions. The results should be presented in a clear and concise manner, often using tables and figures to facilitate understanding. Crucially, the results should be interpreted within the context of the research questions. A discussion of unexpected results or limitations is also essential for a complete evaluation. The section should also compare the obtained results to those from existing methods if applicable, highlighting improvements or novel contributions. Overall, a well-written ‘Empirical Results’ section should provide compelling evidence to support the claims made in the paper, enhancing the paper’s credibility and impact.
Limitations of RTB#
Relative Trajectory Balance (RTB) shows promise but has limitations. Computational cost is a major concern, particularly for high-dimensional data or complex generative models. The need for off-policy training, while offering flexibility, can also impact sample efficiency. The asymptotic nature of RTB’s correctness implies performance might not be optimal for finite datasets or training durations. Mode collapse, though addressed, could still be a concern for challenging posteriors. Finally, while RTB handles arbitrary constraints, the performance depends heavily on the quality of the prior and the constraint function, highlighting the need for appropriate model selection and potentially further methodological developments to mitigate these issues.
Future Directions#
The “Future Directions” section of this research paper could explore several promising avenues. Extending Relative Trajectory Balance (RTB) to other generative models beyond diffusion models is crucial. This includes exploring its applicability to GANs or VAEs, potentially enhancing their ability to handle complex posterior distributions. Improving sample efficiency is another key area. The current RTB method relies on sampling trajectories, which can be computationally expensive. Investigating alternative training strategies or approximations could significantly improve efficiency. Addressing the challenges of high-dimensional spaces is also important. The paper demonstrates effectiveness in several domains but exploring the scalability and robustness of RTB in much higher dimensions is key. Further research should focus on developing more sophisticated exploration techniques for off-policy training. More efficient methods for discovering modes of high density under the posterior distribution will accelerate learning. Finally, thorough theoretical analysis of RTB’s asymptotic properties and convergence rates in various settings is needed to solidify the foundation of the method.
More visual insights#
More on figures
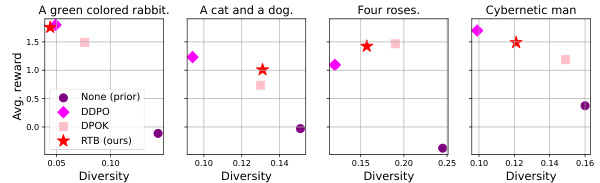
🔼 The figure shows samples from posterior models fine-tuned using the proposed Relative Trajectory Balance (RTB) method. It compares RTB’s performance to other methods, including those based on reinforcement learning (RL) with KL regularization, and classifier guidance. The comparison highlights that RTB effectively samples from the true posterior distribution by achieving both high diversity and closeness to true samples of target classes, unlike RL methods with KL regularization (which show inaccurate inference) and those without (which exhibit mode collapse).
read the caption
Figure 2: Samples from RTB fine-tuned diffusion posteriors.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The prior (a) shows a mixture of 25 Gaussian distributions. The target posterior (b) is obtained by multiplying the prior with a constraint that keeps only 9 of the modes. The figure then displays the sampling densities generated by various methods: (c) shows the proposed RTB method, which closely matches the true posterior; (d) shows RL with KL regularization, which is inaccurate; (e) shows RL without KL regularization which leads to mode collapse; (f) illustrates classifier guidance, which results in biased samples. Section C provides additional details.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.
🔼 This figure compares different posterior inference methods on a 2D Gaussian mixture model. The prior is a mixture of 25 Gaussians, and the posterior is obtained by masking all but 9 of those Gaussians. The figure shows that the proposed Relative Trajectory Balance (RTB) method accurately samples from the true posterior distribution, while other methods like Reinforcement Learning (RL) with KL regularization and classifier guidance either produce inaccurate or mode-collapsed results.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The prior distribution (a) is a mixture of 25 Gaussian components. A posterior distribution (b) is created by multiplying the prior with a constraint that keeps only 9 of the components. The figure then displays the samples generated by several methods: (c) the proposed Relative Trajectory Balance (RTB) method; (d) Reinforcement Learning (RL) with KL regularization; (e) RL without KL regularization; and (f) Classifier Guidance (CG). The results show that only RTB accurately samples the true posterior while the other methods either produce inaccurate or mode-collapsed results.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a 2D Gaussian mixture model. The goal is to sample from a posterior distribution that is the product of a prior (a mixture of 25 Gaussians) and a constraint that selects only 9 of the modes. The figure shows that the proposed method (RTB) effectively samples from the target posterior, unlike other methods such as Reinforcement Learning with and without KL regularization and Classifier Guidance, which either produce inaccurate or mode-collapsed results.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a 2D Gaussian mixture model. The prior (a) is a mixture of 25 Gaussians. The posterior (b) is obtained by multiplying the prior with a constraint that keeps only 9 of the modes. The figure shows that Relative Trajectory Balance (RTB) effectively samples from the posterior distribution, while other methods (Reinforcement Learning with and without KL regularization, Classifier Guidance) either produce inaccurate results or suffer from mode collapse.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares the sampling densities of different posterior inference methods on a two-dimensional Gaussian mixture model. The prior distribution is a mixture of 25 Gaussians. The posterior distribution is obtained by multiplying the prior with a constraint that keeps only 9 of the 25 modes. The figure shows that the proposed Relative Trajectory Balance (RTB) method effectively samples from the target posterior distribution. In contrast, Reinforcement Learning (RL) methods, with or without KL regularization, either mode collapse or produce inaccurate results, while the Classifier Guidance (CG) approximation leads to biased samples.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The prior (a) shows 25 modes, while the true posterior (b) masks all but 9 modes due to a constraint. The figure demonstrates that the proposed Relative Trajectory Balance (RTB) method accurately samples from the true posterior (c), while other methods either fail (RL, classifier guidance) or mode collapse (RL without regularization).
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The goal is to sample from a posterior distribution that’s a product of a prior distribution (a mixture of 25 Gaussians) and a constraint function that keeps only 9 of the modes. The figure shows that the proposed Relative Trajectory Balance (RTB) method accurately samples from this posterior. In contrast, Reinforcement Learning (RL) methods, with or without KL regularization, produce either inaccurate or mode-collapsed results. Classifier guidance also leads to biased sampling.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The goal is to sample from a posterior distribution (panel b) that is obtained by multiplying the prior distribution (a) by a constraint function that masks most of the modes. The figure demonstrates the sampling densities resulting from several methods: (c) Relative Trajectory Balance (RTB), (d) Reinforcement Learning (RL) with KL-regularization, (e) RL without KL-regularization, (f) classifier guidance. RTB shows the closest approximation to the true posterior density.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares the sampling densities produced by different posterior inference methods on a mixture of 25 Gaussians. The goal is to sample from a posterior distribution obtained by multiplying the prior (a mixture of 25 Gaussians) with a constraint that keeps only 9 of the modes. The figure shows that RTB effectively samples the true posterior, while other methods (RL with/without KL regularization, classifier guidance) either fail to accurately represent the posterior or suffer from mode collapse or biased sampling.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

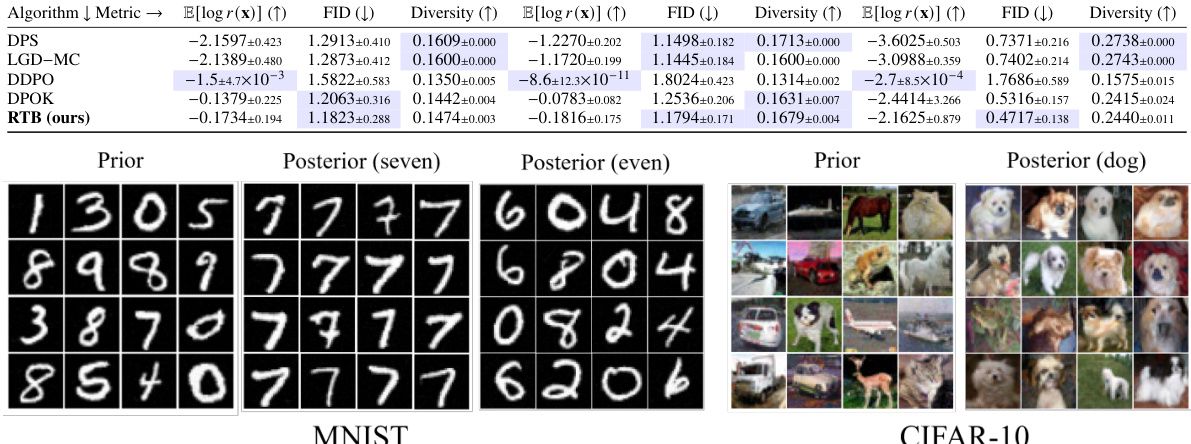
🔼 This figure shows samples generated from posterior models fine-tuned using the Relative Trajectory Balance (RTB) method. It compares RTB’s performance to other methods on MNIST and CIFAR-10 datasets for class-conditional image generation. The results illustrate RTB’s ability to generate diverse and high-quality samples while maintaining adherence to the target class, unlike other methods which demonstrate mode collapse or biased sampling.
read the caption
Figure 2: Samples from RTB fine-tuned diffusion posteriors.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. It shows that the proposed Relative Trajectory Balance (RTB) method accurately samples from the target posterior distribution, whereas other methods like Reinforcement Learning (RL) with or without KL regularization, and Classifier Guidance (CG) fail to do so, either producing inaccurate results or suffering from mode collapse.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The goal is to sample from a posterior distribution that is the product of a prior distribution (a mixture of 25 Gaussians) and a constraint function. The figure shows that the proposed Relative Trajectory Balance (RTB) method accurately samples from the posterior, while other methods like Reinforcement Learning (RL) with and without KL regularization, and Classifier Guidance (CG) fail to do so, either due to inaccurate inference, mode collapse, or biased sampling.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The goal is to sample from a target posterior distribution that is the product of a prior distribution (a mixture of 25 Gaussians) and a constraint that selects only 9 of the modes. The figure shows that the proposed Relative Trajectory Balance (RTB) method accurately samples from the target posterior, while several alternative methods (reinforcement learning with and without KL regularization, and classifier guidance) fail to do so, either producing inaccurate samples or suffering from mode collapse (where only a subset of the modes are sampled).
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The prior distribution is a mixture of 25 Gaussians, and the posterior is obtained by multiplying this prior with a constraint that keeps only 9 of the modes. The figure visualizes the sample densities produced by different methods: the true posterior, the proposed Relative Trajectory Balance (RTB) method, Reinforcement Learning (RL) methods with and without KL regularization, and Classifier Guidance (CG). RTB is shown to better approximate the true posterior compared to other methods.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a 2D Gaussian mixture model. The goal is to sample from a posterior distribution created by multiplying a prior (a mixture of 25 Gaussians) with a constraint that selects only 9 of the modes. The figure shows that the proposed method (RTB) effectively samples from the target posterior, while other methods (RL with/without KL regularization, Classifier Guidance) either produce inaccurate results or suffer from mode collapse.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. It shows that the proposed Relative Trajectory Balance (RTB) method accurately samples from the target posterior distribution, unlike other methods such as Reinforcement Learning (RL) with and without KL regularization, and Classifier Guidance (CG), which suffer from inaccurate inference or mode collapse.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.

🔼 This figure compares different posterior inference methods on a two-dimensional Gaussian mixture model. The methods are evaluated on their ability to sample from a posterior distribution defined by a product of a prior distribution (a mixture of 25 Gaussians) and a constraint that keeps only 9 of the modes. The figure shows that the proposed Relative Trajectory Balance (RTB) method accurately samples from the posterior distribution, while other methods such as Reinforcement Learning (RL) with and without KL regularization, and Classifier Guidance (CG), fail to accurately sample the distribution.
read the caption
Figure 1: Sampling densities learned by various posterior inference methods. The prior is a diffusion model sampling a mixture of 25 Gaussians (a) and the posterior is the product of the prior with a constraint that masks all but 9 of the modes (b). Our method (RTB) samples close to the true posterior (c). RL methods with tuned KL regularization yield inaccurate inference (d), while without KL regularization, they mode-collapse (e). A classifier guidance (CG) approximation (f) results in biased outcomes. For details, see §C.
More on tables
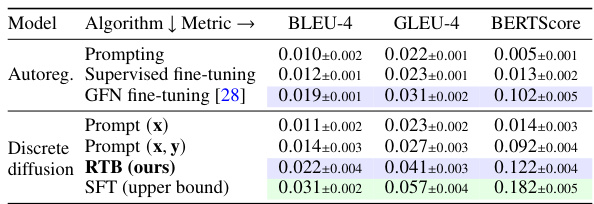
🔼 This table presents the results of a text infilling task using different language models. The task involves predicting a missing sentence in a short story, given the preceding and following sentences. The models compared include an autoregressive language model, a discrete diffusion language model, and a discrete diffusion language model fine-tuned using the Relative Trajectory Balance (RTB) method. The evaluation metrics used are BLEU-4, GLEU-4, and BERTScore, all of which measure the similarity between the generated text and the reference text. The results show that the RTB-fine-tuned model outperforms the other models, indicating the effectiveness of RTB for improving text infilling.
read the caption
Table 3: Results on the story infilling task with autoregressive and discrete diffusion language models. Metrics are computed with respect to reference infills from the dataset. All metrics are mean±std over 5 samples for each of the 100 test examples. RTB with discrete diffusion prior performs better than best baseline with autoregressive prior.
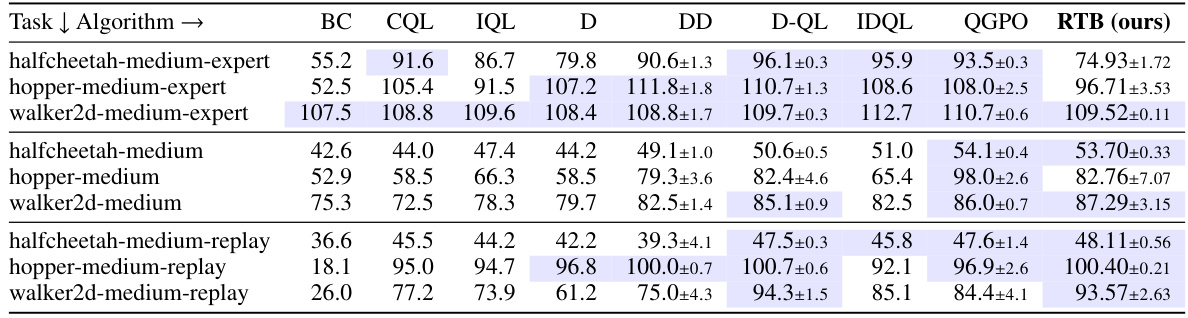
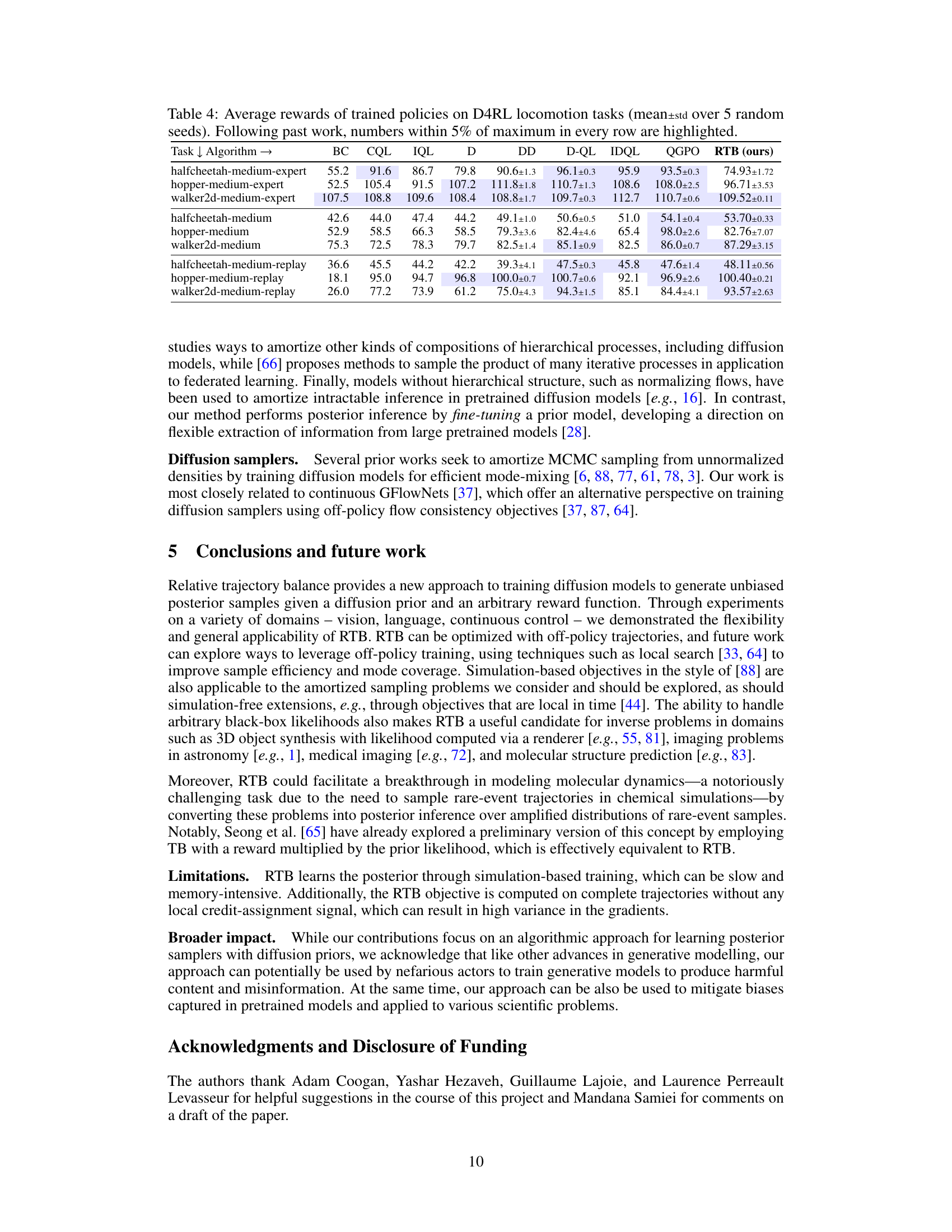
🔼 This table presents the average rewards achieved by different offline reinforcement learning algorithms on three continuous control tasks from the D4RL benchmark. The tasks involve locomotion with a half-cheetah, hopper, and walker2d robot. Three different datasets are used for each task, representing varying levels of data quality (medium-expert, medium, medium-replay). The algorithms compared include several baselines (BC, CQL, IQL) and state-of-the-art diffusion-based offline RL methods (Diffuser, Decision Diffuser, D-QL, IDQL, QGPO), along with the proposed RTB method. The table highlights the top-performing algorithms for each task and dataset by bolding the values within 5% of the maximum reward for that row.
read the caption
Table 4: Average rewards of trained policies on D4RL locomotion tasks (mean±std over 5 random seeds). Following past work, numbers within 5% of maximum in every row are highlighted.

🔼 This table presents the results of classifier-guided posterior sampling experiments using pretrained unconditional diffusion priors. It compares the performance of several methods, including Relative Trajectory Balance (RTB), on MNIST and CIFAR-10 datasets. Metrics such as expected log-likelihood of the classifier, FID (Fréchet Inception Distance), and diversity are reported to assess the quality of posterior samples generated by each method. The table highlights that RTB achieves comparable or better performance compared to other methods in balancing reward and diversity, successfully addressing issues like mode collapse observed in other approaches.
read the caption
Table 2: Classifier-guided posterior sampling with pretrained unconditional diffusion priors. We report the mean±std of each metric computed across all relevant classes for each experiment set, and highlight ±5% from highest/lower experimental value. The FID is computed between learned posterior samples and the true samples from the class in question. DP and LGD-MC fail to appropriately model the posterior distribution (high average logr(x)) while DDPO mode-collapses. RTB achieves comparable or superior performance to all other baselines, optimally balancing high reward and diversity as measured by FID. See Table E.1 for conditional variants.

🔼 This table presents a quantitative comparison of different posterior sampling methods for classifier-guided image generation. It shows the performance of several methods (including the proposed RTB method) across multiple metrics such as FID (Fréchet Inception Distance), diversity, and the average log-likelihood of the constraint. The results demonstrate that the Relative Trajectory Balance (RTB) method outperforms existing methods in terms of balancing high reward and diversity.
read the caption
Table 2: Classifier-guided posterior sampling with pretrained unconditional diffusion priors. We report the mean±std of each metric computed across all relevant classes for each experiment set, and highlight ±5% from highest/lower experimental value. The FID is computed between learned posterior samples and the true samples from the class in question. DP and LGD-MC fail to appropriately model the posterior distribution (high average logr(x)) while DDPO mode-collapses. RTB achieves comparable or superior performance to all other baselines, optimally balancing high reward and diversity as measured by FID. See Table E.1 for conditional variants.

🔼 This table presents a quantitative comparison of different methods for classifier-guided posterior sampling using pretrained unconditional diffusion models. It shows the performance of several methods, including Relative Trajectory Balance (RTB), on MNIST and CIFAR-10 datasets, evaluating metrics such as expected log-likelihood of the constraint (E[logr(x)]), Fréchet Inception Distance (FID), and diversity. The results demonstrate that RTB achieves a better balance between high reward and diversity, and outperforms existing approaches. Conditional variants are also noted.
read the caption
Table 2: Classifier-guided posterior sampling with pretrained unconditional diffusion priors. We report the mean±std of each metric computed across all relevant classes for each experiment set, and highlight ±5% from highest/lower experimental value. The FID is computed between learned posterior samples and the true samples from the class in question. DP and LGD-MC fail to appropriately model the posterior distribution (high average logr(x)) while DDPO mode-collapses. RTB achieves comparable or superior performance to all other baselines, optimally balancing high reward and diversity as measured by FID. See Table E.1 for conditional variants.
🔼 This table presents a comparison of different methods for classifier-guided posterior sampling using pretrained unconditional diffusion priors. The methods are evaluated on their ability to balance high reward and diversity in generated samples. Metrics include the average log-likelihood of the constraint (logr(x)), Fréchet Inception Distance (FID), and diversity. The table highlights the superior performance of Relative Trajectory Balance (RTB) in achieving both high reward and diversity compared to other baselines (DPS, LGD-MC, DDPO, DPOK).
read the caption
Table 2: Classifier-guided posterior sampling with pretrained unconditional diffusion priors. We report the mean±std of each metric computed across all relevant classes for each experiment set, and highlight ±5% from highest/lower experimental value. The FID is computed between learned posterior samples and the true samples from the class in question. DP and LGD-MC fail to appropriately model the posterior distribution (high average logr(x)) while DDPO mode-collapses. RTB achieves comparable or superior performance to all other baselines, optimally balancing high reward and diversity as measured by FID. See Table E.1 for conditional variants.

🔼 This table presents a quantitative comparison of different methods for class-conditional posterior sampling using pretrained unconditional diffusion priors. The methods compared include Density Peak (DPS), Langevin Gradient Descent with Monte Carlo (LGD-MC), Diffusion with DDPM and KL penalty (DDPO), Diffusion with DPOK, and Relative Trajectory Balance (RTB). The table shows the mean and standard deviation of several metrics for each method across all relevant classes, including the expected log-likelihood of the constraint (logr(x)), Fréchet Inception Distance (FID), and diversity. The results demonstrate that RTB outperforms other baselines by balancing high reward and diversity.
read the caption
Table 2: Classifier-guided posterior sampling with pretrained unconditional diffusion priors. We report the mean±std of each metric computed across all relevant classes for each experiment set, and highlight ±5% from highest/lower experimental value. The FID is computed between learned posterior samples and the true samples from the class in question. DP and LGD-MC fail to appropriately model the posterior distribution (high average logr(x)) while DDPO mode-collapses. RTB achieves comparable or superior performance to all other baselines, optimally balancing high reward and diversity as measured by FID. See Table E.1 for conditional variants.

🔼 This table presents the results of classifier-guided posterior sampling experiments using pretrained unconditional diffusion priors. It compares the performance of the proposed Relative Trajectory Balance (RTB) method against several baselines (DPS, LGD-MC, DDPO, DPOK) across different metrics: expected log-likelihood of the constraint (E[logr(x)]), Frechet Inception Distance (FID), and diversity. The results show that RTB outperforms or matches the baselines in balancing high reward and diversity, demonstrating its effectiveness in accurately modeling posterior distributions.
read the caption
Table 2: Classifier-guided posterior sampling with pretrained unconditional diffusion priors. We report the mean±std of each metric computed across all relevant classes for each experiment set, and highlight ±5% from highest/lower experimental value. The FID is computed between learned posterior samples and the true samples from the class in question. DP and LGD-MC fail to appropriately model the posterior distribution (high average logr(x)) while DDPO mode-collapses. RTB achieves comparable or superior performance to all other baselines, optimally balancing high reward and diversity as measured by FID. See Table E.1 for conditional variants.
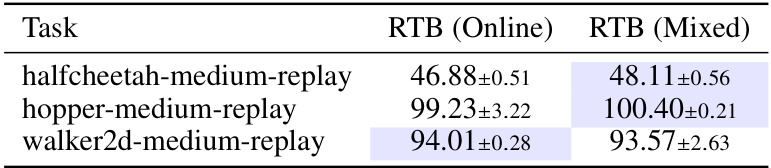
🔼 This table compares the performance of the Relative Trajectory Balance (RTB) method when using two different training approaches on three different tasks from the D4RL benchmark. The ‘Online’ approach uses only online samples from the current policy to update the model parameters. The ‘Mixed’ approach additionally uses offline samples. The table shows the average reward achieved by the trained policy on each task, with standard deviation across five random trials. The results suggest that the mixed training approach can lead to slightly improved performance compared to online training on some tasks, although the differences are not very large for some tasks.
read the caption
Table G.1: Mixed vs. online training on D4RL Tasks. We report mean±std over 5 random seeds.

🔼 This table shows the hyperparameter values of temperature (α) used in the Relative Trajectory Balance (RTB) method for different D4RL tasks. The temperature parameter influences the balance between exploration and exploitation during training.
read the caption
Table G.2: Temperature α = } for D4RL tasks

🔼 This table presents a comparison of different methods for classifier-guided posterior sampling using pretrained unconditional diffusion priors. The methods compared are DPS, LGD-MC, DDPO, DPOK, and the proposed RTB method. The table shows the mean and standard deviation of three metrics: the expected log-likelihood of the constraint (E[log r(x)]), the Frechet Inception Distance (FID) which measures the quality of generated samples, and diversity (measured using cosine similarity). RTB outperforms other methods in balancing reward and diversity.
read the caption
Table 2: Classifier-guided posterior sampling with pretrained unconditional diffusion priors. We report the mean±std of each metric computed across all relevant classes for each experiment set, and highlight ±5% from highest/lower experimental value. The FID is computed between learned posterior samples and the true samples from the class in question. DP and LGD-MC fail to appropriately model the posterior distribution (high average logr(x)) while DDPO mode-collapses. RTB achieves comparable or superior performance to all other baselines, optimally balancing high reward and diversity as measured by FID. See Table E.1 for conditional variants.
Full paper#