TL;DR#
Many machine learning problems, such as multi-task learning and meta-learning, can be formulated as minimax bilevel optimization problems. Existing algorithms are often computationally expensive due to the need for second-order derivatives or memory-intensive storage of model parameters. This poses a significant challenge for their practical application.
This paper tackles this challenge by proposing two novel first-order algorithms: FOSL (fully single-loop) and MemCS (memory-efficient). These algorithms avoid the computationally expensive second-order derivatives. FOSL updates all variables simultaneously, while MemCS uses cold-start initialization to save memory. The paper provides rigorous convergence analyses for both algorithms and shows that their sample complexity matches or exceeds that of existing state-of-the-art algorithms. They demonstrate superior performance across various datasets in deep AUC maximization and robust meta-learning experiments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in multi-task learning, robust machine learning, and few-shot learning because it introduces efficient, first-order algorithms for solving challenging multi-block minimax bilevel optimization problems. Its extensive evaluation and applications to deep AUC maximization and robust meta-learning demonstrate significant performance improvements, paving the way for more effective solutions in these increasingly important areas.
Visual Insights#
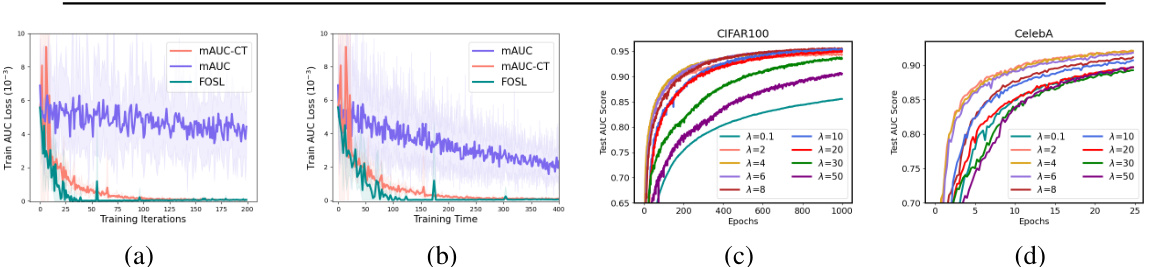
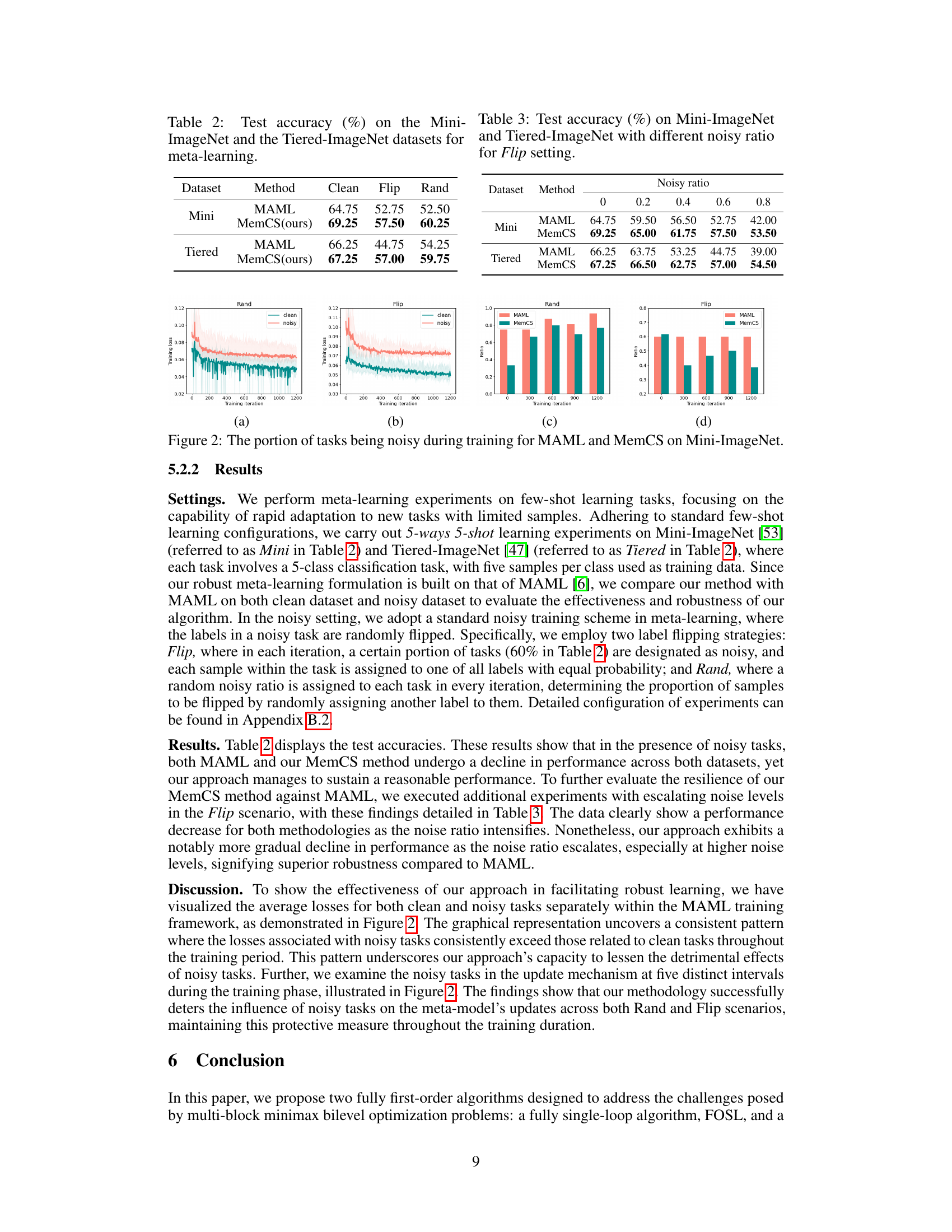
🔼 This figure visualizes the performance of the FOSL algorithm during training for deep AUC maximization. Subfigure (a) shows the training AUC loss against the number of iterations, (b) shows the loss against training time. (c) and (d) illustrate the effect of the hyperparameter λ on the test AUC score for CIFAR100 and CelebA datasets respectively, demonstrating the algorithm’s robustness to different values of λ.
read the caption
Figure 1: Visualization results of FOSL experiments. (a) Training AUC loss over iteration rounds during the initial stages of training. (b) Training AUC loss over time during the initial training phase. (c) Impact of λ on test AUC score throughout training on the CIFAR100 dataset. (d) Impact of λ on test AUC score throughout training on the CelebA dataset.

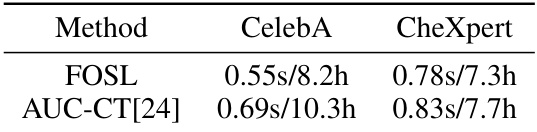
🔼 This table presents the test AUC scores achieved by three different methods (mAUC, mAUC-CT, and FOSL) on four datasets (CIFAR100, CelebA, CheXpert, and OGBG-MolPCBA). The scores represent the area under the receiver operating characteristic curve, a common metric for evaluating the performance of binary classification models. The confidence intervals provide a measure of the uncertainty in these estimates.
read the caption
Table 1: Test AUC score with 95% confidence interval on different datasets for AUC maximization.
In-depth insights#
Bilevel Optimization#
Bilevel optimization presents a powerful framework for tackling problems where the optimization process involves nested optimization problems. The core idea is to optimize an upper-level objective function while simultaneously optimizing a lower-level objective function that is dependent on the upper-level variables. This dependency creates a complex interplay between the two levels, requiring sophisticated algorithms to find solutions. This approach finds applications in various fields, including machine learning, where it helps solve problems like hyperparameter optimization and meta-learning, offering improvements in model performance and robustness. However, solving bilevel problems efficiently is challenging due to their inherent complexity, often requiring advanced techniques such as implicit differentiation, which can be computationally expensive. First-order methods offer a promising approach to mitigating the high computational costs associated with second-order methods, allowing researchers to tackle larger and more complex problems. Recent work focuses on developing efficient and theoretically sound algorithms, addressing challenges related to memory efficiency and scalability. The effectiveness and applicability of these algorithms depend heavily on the properties of the problem’s objective functions, specifically their convexity and smoothness. Future research will likely concentrate on improving the efficiency and applicability of bilevel optimization algorithms, as well as exploring novel applications in other domains.
First-Order Methods#
First-order methods offer a compelling approach to solving optimization problems, particularly in the context of machine learning, where high dimensionality and computational efficiency are crucial. Their advantage lies in their relatively low computational cost per iteration, requiring only the calculation of gradients, unlike second-order methods which necessitate more expensive Hessian computations. This makes first-order methods scalable to large datasets, a significant advantage in many modern applications. However, convergence speed is a key consideration, and first-order methods can sometimes be slow to converge, especially when dealing with non-convex optimization landscapes. Therefore, careful algorithm design and parameter tuning are needed to ensure both efficiency and accuracy. Recent research focuses on developing sophisticated first-order algorithms, such as those incorporating momentum or adaptive learning rates, to mitigate this limitation and improve convergence properties. The choice of a particular first-order method often involves a trade-off between computational cost per iteration and overall convergence speed, making it essential to select the right method based on the specifics of the optimization problem and available resources.
AUC Maximization#
The concept of AUC maximization, focusing on maximizing the area under the ROC curve, is a crucial aspect of imbalanced data classification. Standard approaches often struggle with imbalanced datasets, where the number of samples in different classes varies significantly. AUC maximization directly addresses this challenge by optimizing the AUC score, a metric less susceptible to the class imbalance problem than traditional metrics like accuracy. This is achieved by creating models that accurately rank instances from different classes, instead of focusing solely on precise class assignments. Deep AUC maximization leverages deep learning models to improve the ranking power, further enhancing performance. However, the optimization process for deep AUC maximization methods poses unique difficulties. The problem usually involves a minimax optimization problem, with multiple non-convex functions, leading to computationally intensive methods. The authors of the paper explore new first-order algorithms to address the high cost, leading to potential advancements in applying deep AUC maximization across various applications.
Meta-Learning#
Meta-learning, the process of learning to learn, is a powerful paradigm in machine learning. It aims to improve the efficiency and effectiveness of learning new tasks by leveraging knowledge acquired from previous experiences. The core idea is to learn a meta-model that can rapidly adapt to new tasks with minimal data. Different meta-learning algorithms exist, each with its own strengths and weaknesses. Some approaches focus on optimizing model parameters or learning a good initialization strategy. Others employ learning algorithms that can be quickly adapted to new tasks by learning a small set of parameters. Robust meta-learning is critical, as real-world applications often involve noisy or incomplete data. Approaches here include data filtering, re-weighting, and re-labeling techniques. Meta-learning finds applications in few-shot learning, multi-task learning, and transfer learning. Applications are diverse, spanning image recognition, natural language processing, and robotics. Future work in meta-learning might involve exploring new meta-learning algorithms, investigating the theoretical properties of existing algorithms, and applying meta-learning to more complex real-world applications.
Future Works#
A promising area for future work is extending the proposed first-order algorithms to handle even more complex bilevel optimization problems. This could involve exploring scenarios with non-convex lower-level problems or incorporating constraints into the optimization process. Investigating the impact of different sampling strategies on the convergence rates and sample complexities of the algorithms is also crucial. Another important direction is developing more efficient and robust meta-learning applications. This might include exploring new tasks in areas such as natural language processing or computer vision. Finally, a comprehensive empirical study comparing the performance of the proposed algorithms with state-of-the-art methods across a wide range of benchmark datasets would provide valuable insights and help solidify the practical value of these approaches.
More visual insights#
More on figures
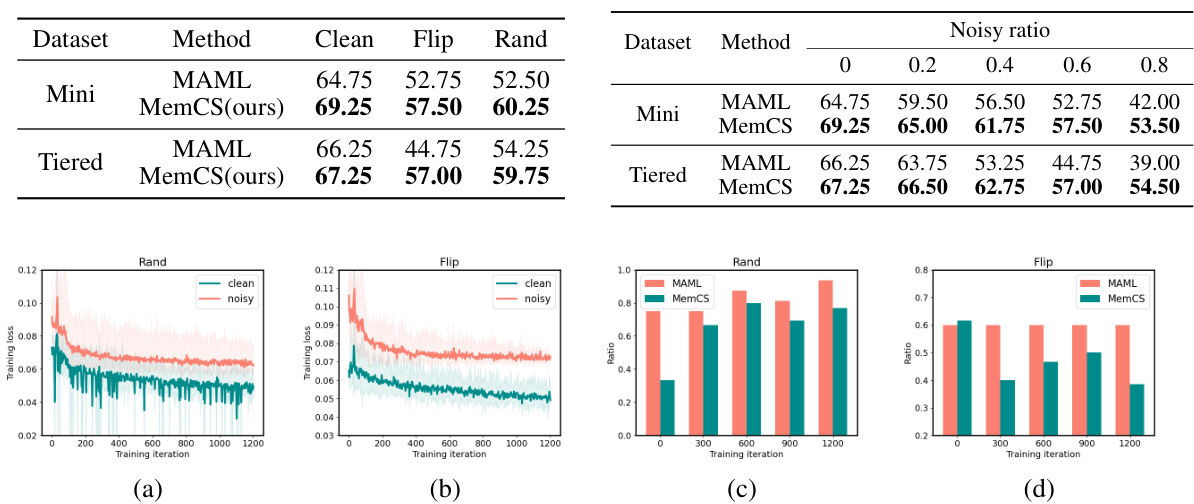
🔼 This figure visualizes the results of the FOSL experiments, demonstrating the training AUC loss over both iteration rounds and training time. It also shows how the hyperparameter λ affects the test AUC score during training on two different datasets, CIFAR100 and CelebA.
read the caption
Figure 1: Visualization results of FOSL experiments. (a) Training AUC loss over iteration rounds during the initial stages of training. (b) Training AUC loss over time during the initial training phase. (c) Impact of λ on test AUC score throughout training on the CIFAR100 dataset. (d) Impact of λ on test AUC score throughout training on the CelebA dataset.

🔼 This figure visualizes the results of the FOSL experiments, showing the training AUC loss over iteration rounds and time, and the impact of the hyperparameter λ on test AUC scores for the CIFAR100 and CelebA datasets. Subfigure (a) and (b) illustrate the training loss curves, demonstrating the convergence speed and stability of the FOSL algorithm. Subfigures (c) and (d) show how the choice of λ affects the test AUC scores across different training epochs for the two datasets.
read the caption
Figure 1: Visualization results of FOSL experiments. (a) Training AUC loss over iteration rounds during the initial stages of training. (b) Training AUC loss over time during the initial training phase. (c) Impact of λ on test AUC score throughout training on the CIFAR100 dataset. (d) Impact of λ on test AUC score throughout training on the CelebA dataset.
🔼 This figure visualizes the performance of the FOSL algorithm during the initial training phase on two datasets, CIFAR100 and CelebA. The left side shows the AUC loss decreasing over training iterations and training time. The right side illustrates how test AUC scores change across different values of hyperparameter λ on each dataset.
read the caption
Figure 1: Visualization results of FOSL experiments. (a) Training AUC loss over iteration rounds during the initial stages of training. (b) Training AUC loss over time during the initial training phase. (c) Impact of λ on test AUC score throughout training on the CIFAR100 dataset. (d) Impact of λ on test AUC score throughout training on the CelebA dataset.
Full paper#